Visualizacin Computacional de Datos I Transformaciones Transformaciones Las

Visualización Computacional de Datos I Transformaciones

Transformaciones Las transformaciones se aplican sobre los puntos que definen el objeto P 1 Pi P 2 Pi = (px, py)

Transformaciones Simples Escala isotrópica Pi = (px, py) S= sx 0 0 sy Pi = S. Pi

Transformaciones Simples Traslación dy dx Pi = Pi + D Pi = (px, py) D = (dx, dy)

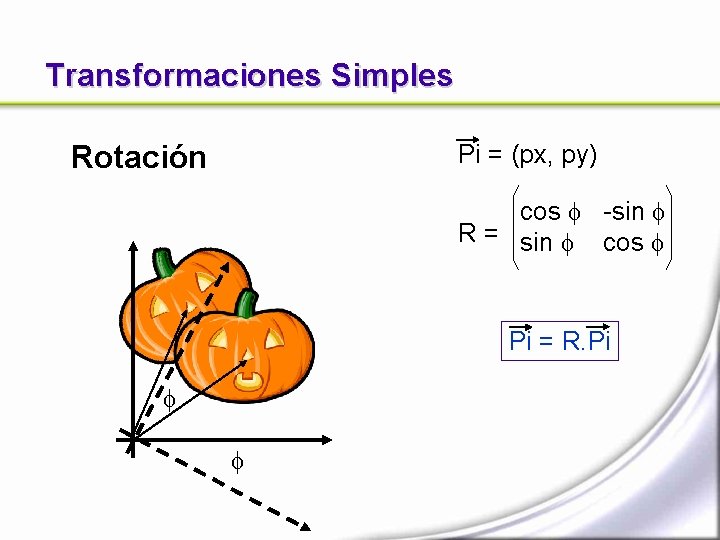
Transformaciones Simples Rotación Pi = (px, py) cos -sin R = sin cos Pi = R. Pi

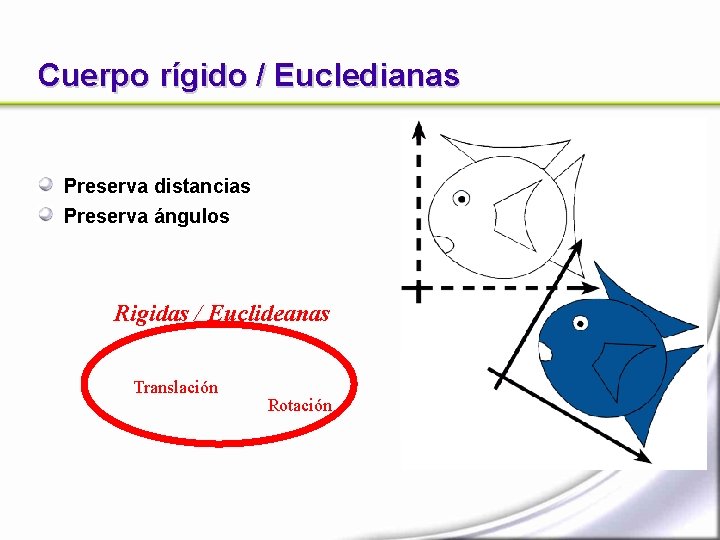
Cuerpo rígido / Eucledianas Preserva distancias Preserva ángulos Rigidas / Euclideanas Translación Rotación

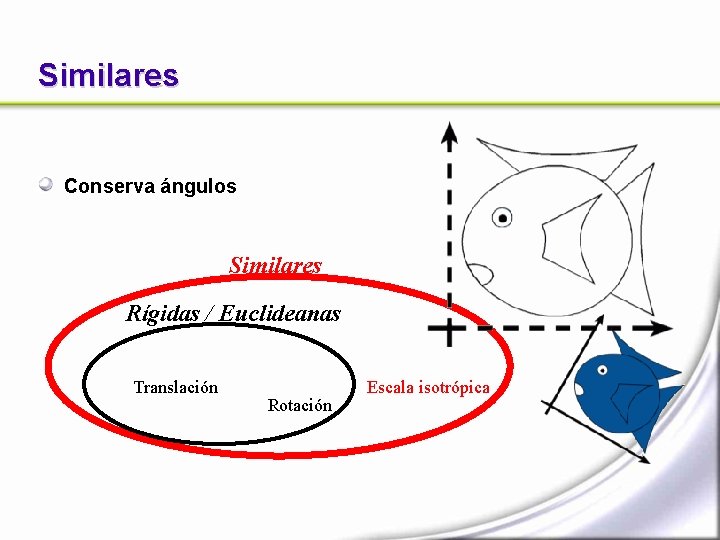
Similares Conserva ángulos Similares Rígidas / Euclideanas Translación Rotación Escala isotrópica

Lineales Similares Rígidas / Eucledianas Translación Rotación Lineales Escala isotrópica Escala Reflexión Shear

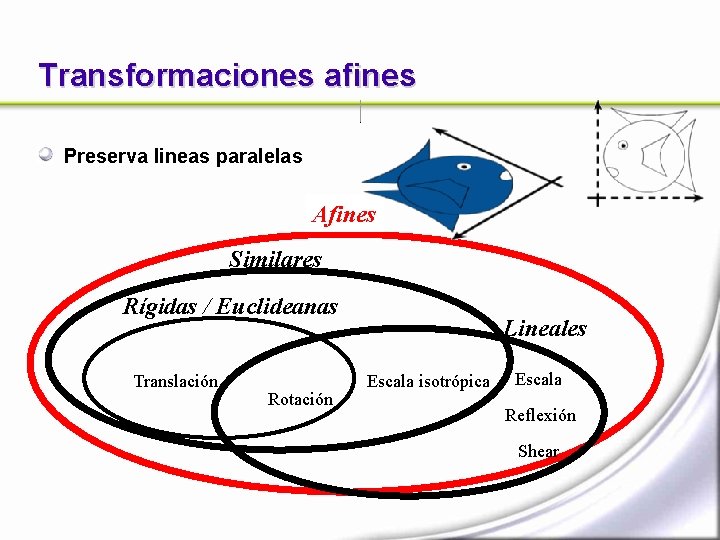
Transformaciones afines Preserva lineas paralelas Afines Similares Rígidas / Euclideanas Translación Rotación Lineales Escala isotrópica Escala Reflexión Shear

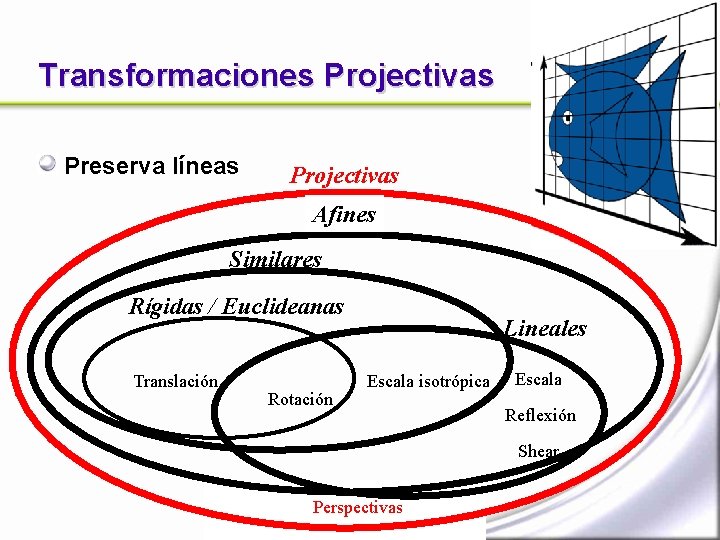
Transformaciones Projectivas Preserva líneas Projectivas Afines Similares Rígidas / Euclideanas Translación Rotación Lineales Escala isotrópica Escala Reflexión Shear Perspectivas

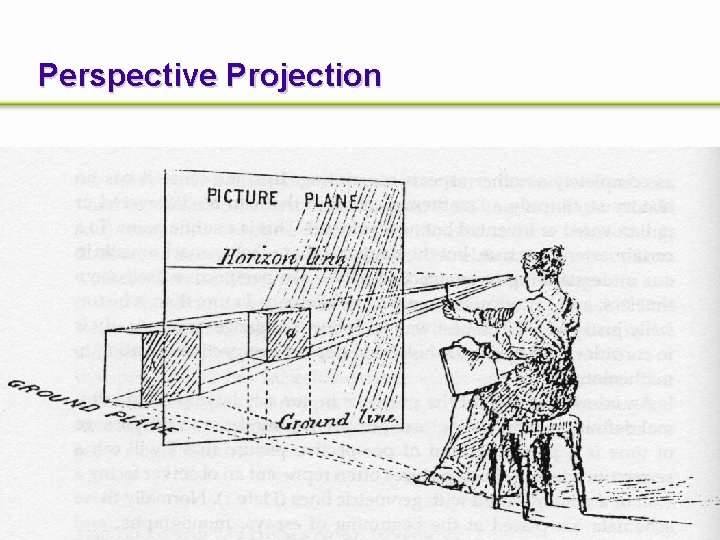
Perspective Projection

General / no lineales No preserva líneas From Sederberg and Parry, Siggraph 1986

Como representar las transformaciones? x' = ax + by + c y' = dx + ey + f x' = y' p' = a d b e Mp x c + y f + t

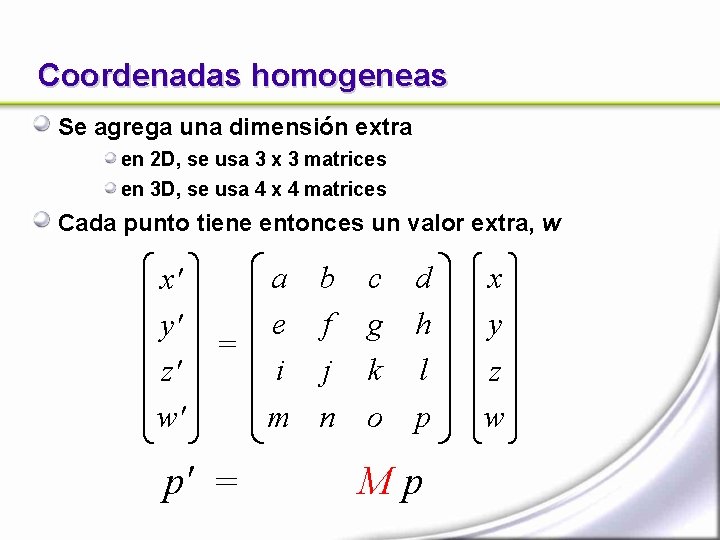
Coordenadas homogeneas Se agrega una dimensión extra en 2 D, se usa 3 x 3 matrices en 3 D, se usa 4 x 4 matrices Cada punto tiene entonces un valor extra, w a b x' e f y' = i j z' m n w' c g k o d h l p p' = Mp x y z w

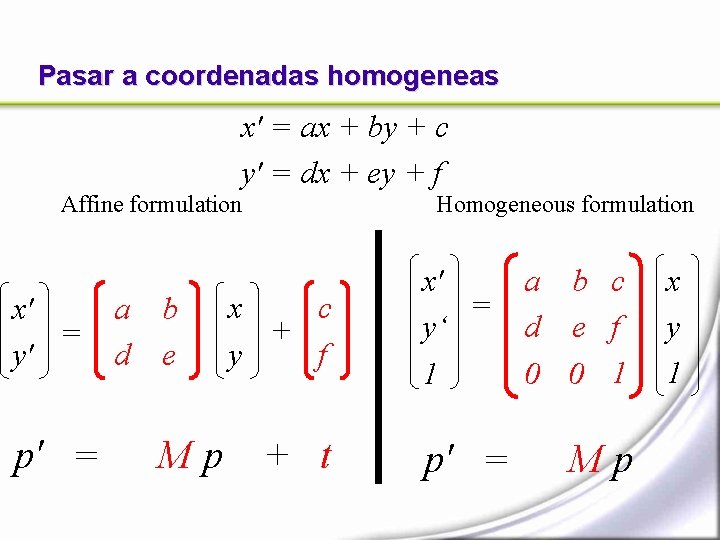
Pasar a coordenadas homogeneas x' = ax + by + c y' = dx + ey + f Affine formulation x' = y' p' = a d b e x c + y f Mp + t Homogeneous formulation x' = y‘ 1 p' = a b c d e f 0 0 1 Mp x y 1

Translación (tx, ty, tz) Por que utilizar coordenadas homogeneas? Porque ahora traslaciones se expresan como matriz! x' y' z' 10 = 1 0 0 0 0 1 0 tx ty tz 1 x y z 1

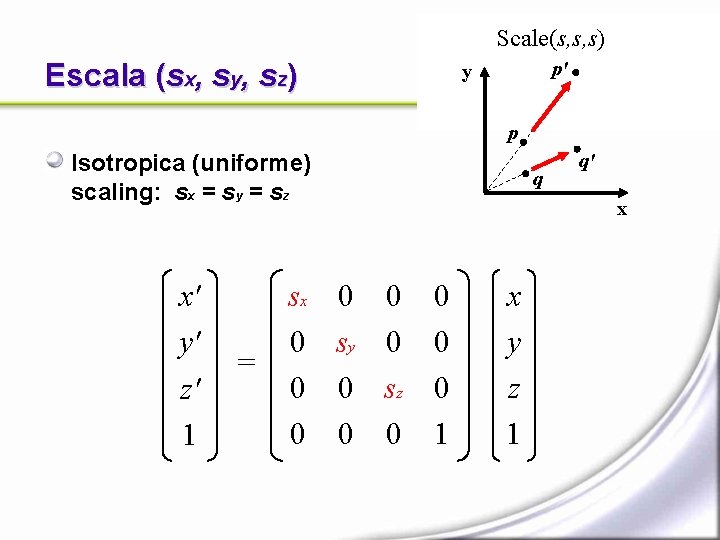
Scale(s, s, s) Escala (sx, sy, sz) p' y p Isotropica (uniforme) scaling: sx = sy = sz x' y' z' 1 sx 0 = 0 0 q q' x 0 sy 0 0 sz 0 0 1 x y z 1

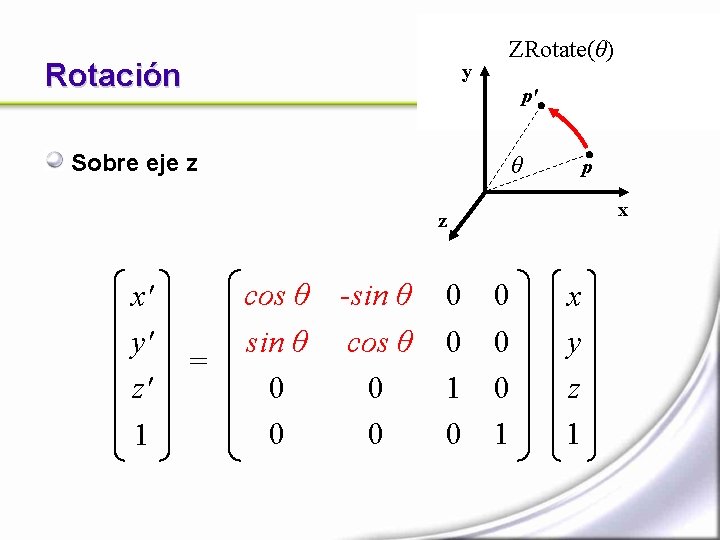
Rotación y ZRotate(θ) p' Sobre eje z θ p x z x' y' z' 1 = cos θ -sin θ cos θ 0 0 0 1 x y z 1