Aritmtica Computacional Francisco Rodrguez Henrquez CINVESTAV franciscocs cinvestav

Aritmética Computacional Francisco Rodríguez Henríquez CINVESTAV francisco@cs. cinvestav. mx Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Anuncios Importantes • 1 examen 30 puntos • Proyecto: propuesta, avance y Presentación 70 puntos • Quizzes Aritmética Computacional Invierno 2005 [1 punto cada uno] Francisco Rodríguez Henríquez

Teoría elemental de números: definiciones y teoremas Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Definiciones El conjunto de enteros {…, -3, -2, -1, 0, 1, 2, 3, …} se dentoa por el símbolo Z. Sean a, b dos enteros positivos. Entonces se dice que a divide a b si existe un entero c tal que b = ac. El hecho que a divida a b se denota como a|b. Ejemplos: -3|18, puesto que 18 = (-3)(-6); cualquier entero a divide a 0, a|0, puesto que 0 = (a)(0). Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Definiciones: enteros Las siguientes son algunas propiedades elementales de la divisibilidad: Resultado: (propiedades de la divisibilidad) Para todo a, b, c, Z, se cumple lo siguiente: i. a|a ii. Si a|b y b|c, entonces a|c iii. Si a|b y a|c, entonces a|(bx+cy) para todo x, y Z. iv. Si a|b y b|a, entonces a = ±b Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Definiciones: división entera Definición (algoritmo de división entera) Si a y b son enteros con b≥ 1, entonces la división entera de a por b define los enteros q (el cociente) y r (el residuo) tal que a = qb+r, donde 0 ≤ r <b Donde q y r son únicos. El residuo de una divisón se denota como a mod b, mientras que el cociente se denota como a div b. Definición Un entero c es un divisor común de a y b si c|a y c|b. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Definiciones: MCD Definición Se dice que un entero no negativo d es el máximo común divisor de los enteros a y b, i. e. d = MCD(a, b), Si: i. d es un divisor común de a y b; y ii. Si existe un número c tal que c|a and c|b, entonces c|d. De manera equivalente, MCD(a, b) es el entero positivo más grande que divide tanto a a como a b, con la excepción de MCD(0, 0) = 0. Definición Se dice que dos enteros a y b son primos relativos o co-primos si MCD(a, b)=1 Definición Se dice que un entero p≥ 2 es primo si y sólo si sus únicos divisores positivos son 1 y p. De otra manera, se dice que p es un número compuesto. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Definiciones: mcm Definición Un entero no negativo d es el mínimo común múltiplo a y b, i. e. d = mcm(a, b), si i. a|d y b|d; y ii. Para todo a|c y b|c, se cumple que d|c. De manera equivalente, mcm(a, b) es el entero positivo más pequeño que es divisible tanto por a como por b. Resultado Si a y b son enteros positivos, entonces mcm(a, b)=a*b/GCD(a, b). Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Definitions: Prime Numbers Definition An integer p≥ 2 is said to be prime if its only positive divisor are 1 and p. Otherwise, p is called composite. Fact If p is prime and p|ab, then either p|a or p|b or both. (is it true if p is composite? ). Fact There an infinite number of prime numbers (how can we prove it? ) Fact (prime number theorem) Let (x) denote the number of prime numbers ≤ x. Then Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Definitions: Prime Numbers Fact (upper and lower bounds for (x)). Let (x) denote the number of prime numbers ≤ x. Then for x≥ 17 and for x > 1, Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Fundamental Theorem of Arithmetic • Every integer n ≥ 2 has a factorization as a product of prime powers: • Where the pi are distinct primes, and the ei are positive integers. Furthermore, the factorization is unique up to the rearrangement of factors. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Fundamental Theorem of Arithmetic • Proof: existence [sketch] Suppose there exist positive integers that are not product of primes. Let n be the smallest such integer. Then n cannot be 1 or a prime, so n must be composite. Therefore n = ab with 1 < a, b < n. Since n is the smallest positive integer that is not a product of primes, both a and b are product of primes. But a product of primes times a product of primes is a product of primes, so n = ab is a product of primes. Therefore, every positive integer is a product of primes. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Fundamental Theorem of Arithmetic • Proof: uniqueness [sketch] If p is a prime and p divides a product of integers ab, then either p|a or p|b (or both!), Suppose that an integer n can be written as a product of primes in two different ways: • If a prime occurs in both factorizations divide both sides by it to obtain a shorter relation. Now take a prime that occurs on the left side, say p 1. Since p 1 divides n then it must divide one of the factors of the right side, say qj. But since p 1 is prime, we are forced to write p 1= qj, which is a contradiction with the original hyphotesis. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Prime Numbers: How many? Fact There an infinite number of prime numbers (how can we prove it? ) Euclid did it! But how? Should we have a quizz? ? Hint: Follow the same line of reasoning used for FTA… Any idea? ? ? Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Fundamental Theorem of Arithmetic • Fact If where each ei ≥ 0 and fi ≥ 0, then Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Fundamental Theorem of Arithmetic Example: Let a = 4864 = 28 19, b = 3458 = 2 7 13 19. Then gcd(4864, 3458) = 2 19 = 38 and, lcm(4864, 3458)= 28 7 13 19 = 442624 Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Definitions: Euler phi Function Definition For n ≥ 1, let (n) denote the number on integers in the interval [1, n], which are relatively prime to n. The function is called the Euler phi function (or the Euler totient function). Fact (properties of Euler phi function) i. If p is a prime, then (p) = p-1. ii. The Euler phi function is multiplicative. That is, if gcd(m, n) = 1, then (mn) = (m) (n). Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Definitions: Euler phi Function iii. If then is the prime factorization of n, iv. For all integers n ≥ 5, Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Máximo común divisor • El máximo común divisor (a, b) de a y b es el entero más grande que divide exactamente a ambos números. Se usa el algoritmo de Euclides para hallar el máximo común divisoe (mcd) de dos números a y n, a<n Observación: Si a y b tienen un divisor d también lo tienen a-b, a-2 b. mcd (a, n) puede ser hallado como: Sea g 0=n; g 1=a; gi+1 = gi-1 mod gi Cuando gi=0 then (a, n) = gi-1 Ejemplo: hallar (56, 98) g 0 = 98; g 1=56; g 2 = 98 mod 56 = 42; g 3 = 56 mod 42 = 14; g 4 = 42 mod 14 = 0; Entonces (56, 98)=14. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

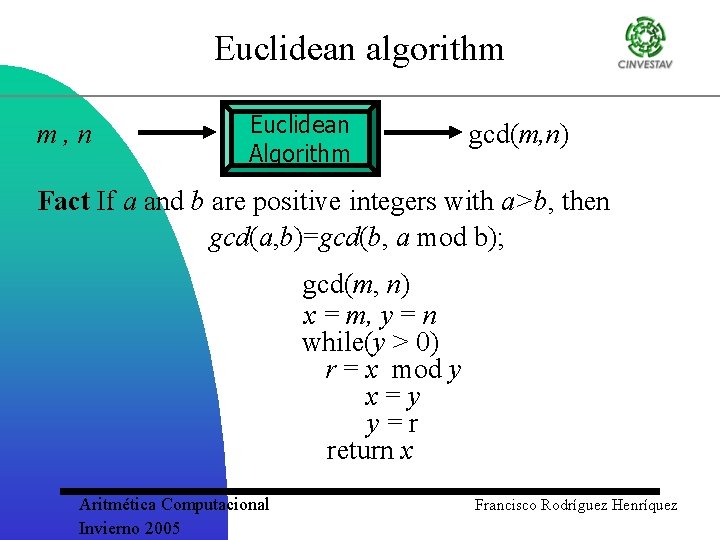
Euclidean algorithm m, n Euclidean Algorithm gcd(m, n) Fact If a and b are positive integers with a>b, then gcd(a, b)=gcd(b, a mod b); gcd(m, n) x = m, y = n while(y > 0) r = x mod y x=y y=r return x Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Euclidean algorithm Example The following are the division steps for computing gcd(4864, 3458) = 38: 4864 = 1*3458 + 1406 3458 = 2*1406 + 646 1406 = 2*646 + 114 646 = 5*114 + 76 114 = 1*76 + 38 76 = 2*38 + 0 (Which method is more efficient and why? ? ) Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

gcd: Computational Complexity Assuming mod operation complexity is K: integer euclid(m, n) x = m, y = n while( y > 0) r = x mod y x=y y=r return x K+ ¿? ( O (1) + K + O (1) ) + O (1) = ¿? K O(1) Where “¿? ” is the number of while-loop iterations. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

gcd: Computational Complexity Facts: (x’ = next value of x, etc. ) 1. x can only be less than y at very beginning of algorithm –once x > y, x’ = y > y’ = x mod y 2. When x > y, two iterations of while loop guarantee that new x is < ½ original x –because x’’ = y’ = x mod y. Two cases: I. II. y > ½ x x mod y = x – y < ½ x y ≤ ½ x x mod y < y ≤ ½ x Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

gcd: Computational Complexity (1&2) After first iteration, size of x decreases by factor > 2 every two iterations. i. e. after 2 i+1 iterations, x < original_x / 2 i Q: When –in terms of number of iterations i– does this process terminate? Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

gcd: Computational Complexity After 2 i+1 steps, x < original_x / 2 i A: While-loop exits when y is 0, which is right before “would have” gotten x = 0. Exiting while-loop happens when 2 i > original_x, (why? ? ) so definitely by: i = log 2 ( original_x ) Therefore running time of algorithm is: O(2 i+1) = O(i) = O (log 2 (max (a, b)) ) Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

gcd: Computational Complexity Measuring input size in terms of n = number of digits of max(a, b): n = (log 10 (max(a, b)) ) = (log 2 (max(a, b)) ) Therefore running time of algorithm is: O(log 2 (max(a, b)) ) = O(n) (Except fot the mod operation complexity K, which in general is operand-size dependant) A more formal derivation of the complexity of Euclidean gcd can be found in section 4. 5. 3, Volume II of Knuth’s “The Art of Computing Programming” Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Euclidean gcd: Revisited Properties: i. By definition gcd(0, 0) = 0. ii. gcd(u, v) = gcd(v, u) iii. gcd(u, v) = gcd(-u, v) iv. gcd(u, 0) = |u| v. gcd(u, v)w = gcd(uw, vw) if w ≥ 0 vi. lcm(u, v)w = lcm(uw, vw) if w ≥ 0 vii. uv = gcd(u, v) lcm(u, v) if u, v ≥ 0 viii. gcd(lcm(u, v), lcm(u, w)) = lcm(u, gcd(v, w)); ix. lcm(gcd(u, v), gcd(u, w)) = gcd(u, lcm(v, w)) Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Euclidean gcd Revisited Binary Properties: i. If u and v are both even, then gcd(u, v) = 2 gcd(u/2, v/2); i. If u is even and v is odd, then gcd(u, v) = gcd(u/2, v); i. gcd(u, v) = gcd(u-v, v). ii. If u and v are both odd, then u-v is even and |u-v| < max(u, v). Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Binary gcd algorithm Input: u, v positive integers, such that u > v. Output: w = gcd(u, v). 1. for (k = 0; u, v both even; k++) { u /= 2; v /= 2; }; /* [Find power of 2] */ 2. [Initialize] if (u is odd) t =-v else t = u; 3. [halve t] while (t is even) t /= 2; 4. if (t > 0) u = t else v = -t; 5. [Subtract] t = u-v. If t ≠ 0 go back to 3, otherwise output w = u 2 k. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Binary gcd algorithm: Example find the gcd of u =40902, v = 24140. t -12070, -6035 +14416, +901 u 40902 20451 v 24140 6035 -5134, -2567 -1666, -833 +68, +34, +17 -816, -51 -34, -17 901 901 17 17 6035 2567 833 51 0 17 17 Aritmética Computacional Invierno 2005 w=17*21=34 Francisco Rodríguez Henríquez

Extended Euclidean Algorithm The Euclidean algorithm can be extended so that it not only yields the greatest common divisor d of two integers a and b, but also generates x and y satisfying ax +by = d. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Modular Inverses THM 1: e has an inverse modulo N if and only if e and N are relatively prime. This will follow from the following useful fact. THM 2: If a and b are positive integers, the gcd of a and b can be expressed as an integer combination of a and b. I. e. , there are integers s, t for which gcd(a, b) = sa + tb Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Modular Inverses Proof of THM 1 using THM 2: If an inverse d exists for e modulo N, we have de 1 (mod N) so that for some k, de = 1 +k. N, so 1 = de – k. N. This equation implies that any number dividing both e and N must divide 1, so must be 1, so e, N are relatively prime. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Modular Inverses On the other hand, suppose that e, N are relatively prime. Using THM 2, write 1 = se + t. N. Rewrite this as se = 1 -t. N. Evaluating both sides mod N gives se 1 (mod N). Therefore s is seemingly the inverse e except that it may be in the wrong range so set d = s mod N. � Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Extended Euclidean Algorithm A constructive version of THM 2 which gives s and t will give explicit inverses. This is what the extended Euclidean algorithm does. The extended Euclidean algorithm works the same as the regular Euclidean algorithm except that we keep track of more details –namely the quotient q = x/y in addition to the remainder r = x mod y. This allows us to backtrack and write the gcd(a, b) as a linear combination of a and b. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

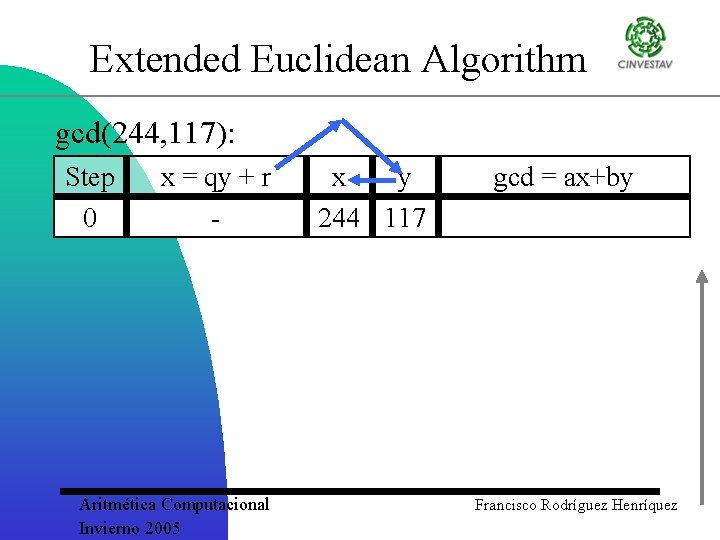
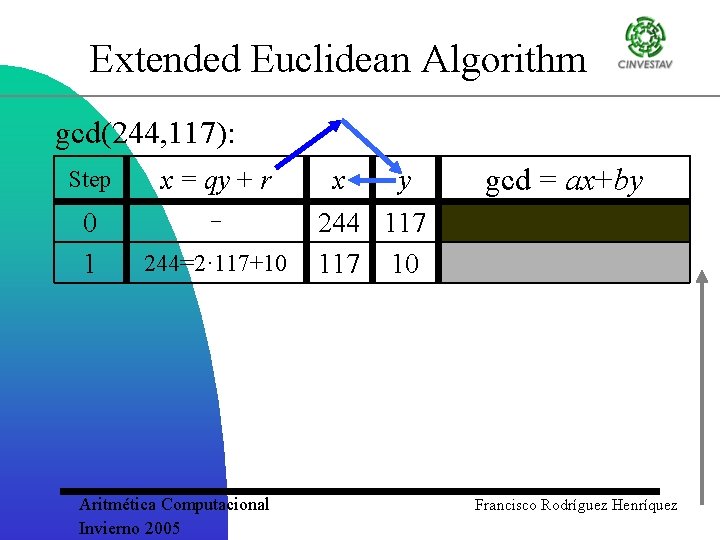
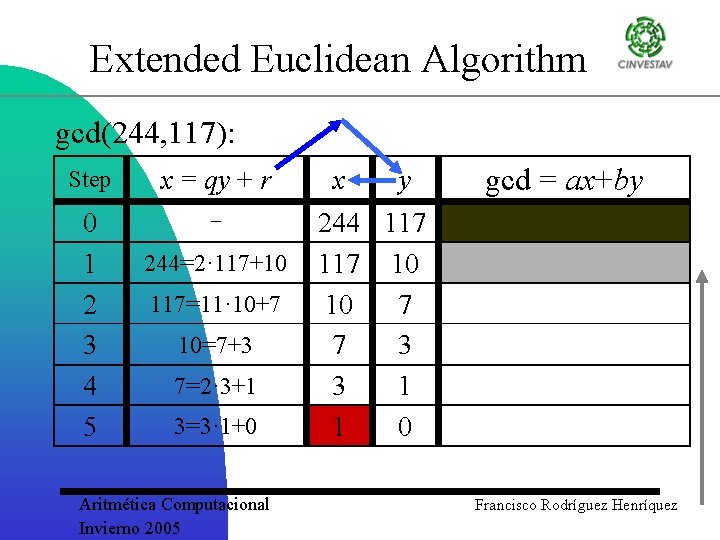
Extended Euclidean Algorithm gcd(244, 117): Step 0 x = qy + r - Aritmética Computacional Invierno 2005 x y 244 117 gcd = ax+by Francisco Rodríguez Henríquez

Extended Euclidean Algorithm gcd(244, 117): Step x = qy + r 0 1 244=2· 117+10 Aritmética Computacional Invierno 2005 x y gcd = ax+by 244 117 10 Francisco Rodríguez Henríquez

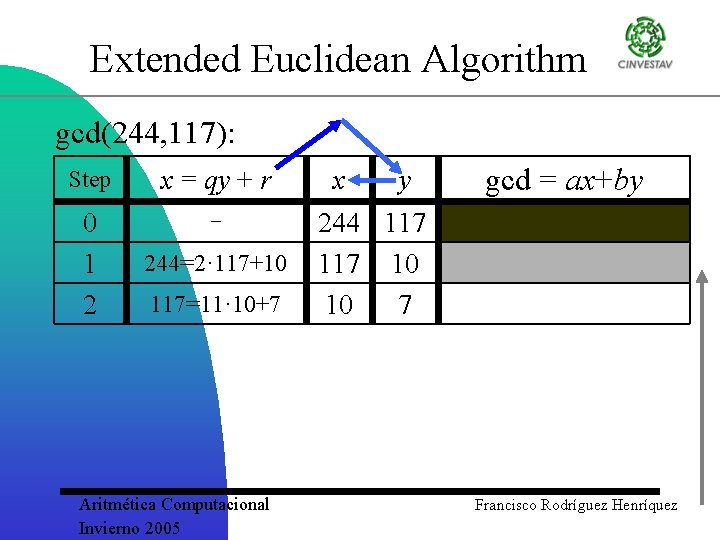
Extended Euclidean Algorithm gcd(244, 117): Step x = qy + r 0 1 2 244=2· 117+10 117=11· 10+7 Aritmética Computacional Invierno 2005 x y gcd = ax+by 244 117 10 10 7 Francisco Rodríguez Henríquez

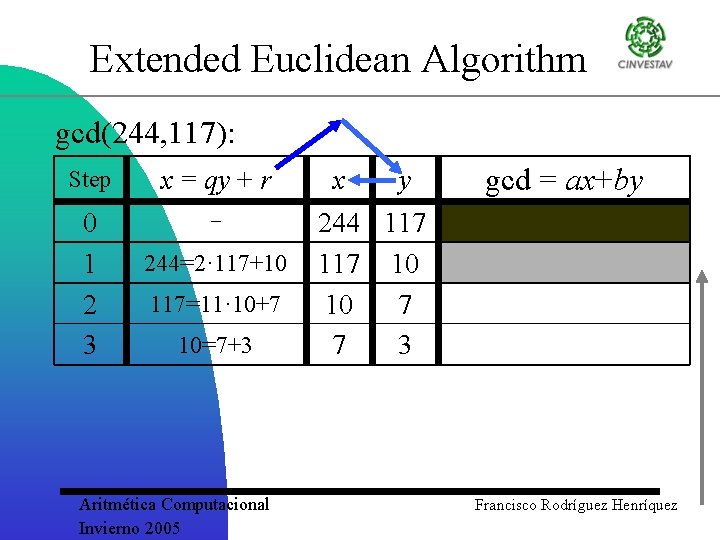
Extended Euclidean Algorithm gcd(244, 117): Step x = qy + r 0 1 2 3 244=2· 117+10 117=11· 10+7 10=7+3 Aritmética Computacional Invierno 2005 x y gcd = ax+by 244 117 10 10 7 7 3 Francisco Rodríguez Henríquez

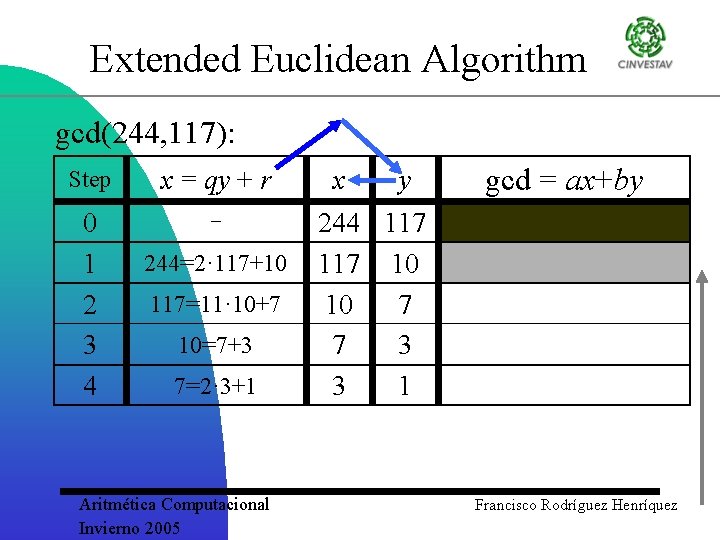
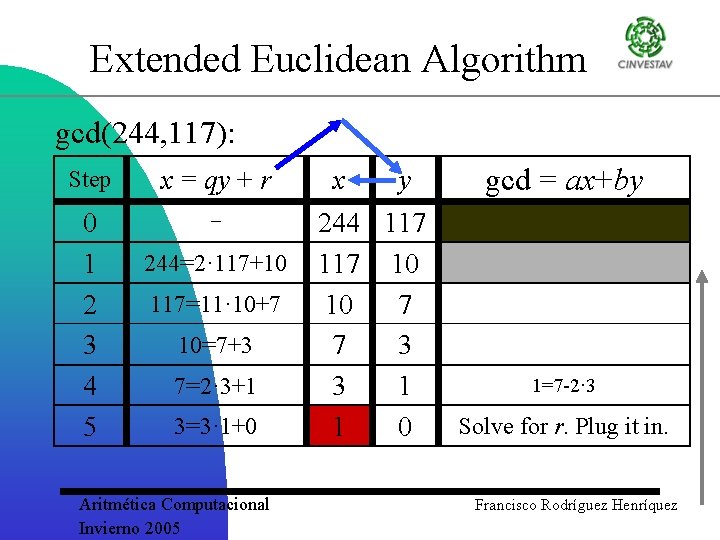
Extended Euclidean Algorithm gcd(244, 117): Step x = qy + r 0 1 2 3 4 244=2· 117+10 117=11· 10+7 10=7+3 7=2· 3+1 Aritmética Computacional Invierno 2005 x y gcd = ax+by 244 117 10 10 7 7 3 3 1 Francisco Rodríguez Henríquez

Extended Euclidean Algorithm gcd(244, 117): Step x = qy + r 0 1 2 3 4 5 244=2· 117+10 117=11· 10+7 10=7+3 7=2· 3+1 3=3· 1+0 Aritmética Computacional Invierno 2005 x y gcd = ax+by 244 117 10 10 7 7 3 3 1 1 0 Francisco Rodríguez Henríquez

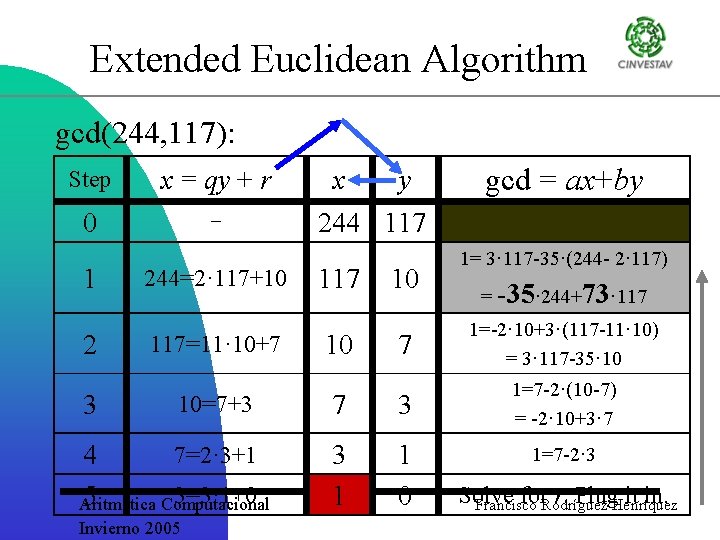
Extended Euclidean Algorithm gcd(244, 117): Step x = qy + r 0 1 2 3 4 5 244=2· 117+10 117=11· 10+7 10=7+3 7=2· 3+1 3=3· 1+0 Aritmética Computacional Invierno 2005 x y 244 117 10 10 7 7 3 3 1 1 0 gcd = ax+by 1=7 -2· 3 Solve for r. Plug it in. Francisco Rodríguez Henríquez

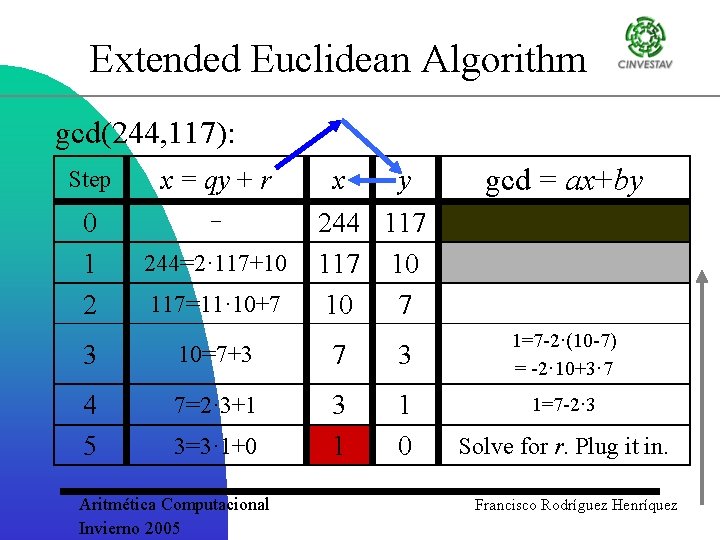
Extended Euclidean Algorithm gcd(244, 117): Step x = qy + r 0 1 2 244=2· 117+10 117=11· 10+7 x y 244 117 10 10 7 3 10=7+3 7 3 4 5 7=2· 3+1 3 1 1 0 3=3· 1+0 Aritmética Computacional Invierno 2005 gcd = ax+by 1=7 -2·(10 -7) = -2· 10+3· 7 1=7 -2· 3 Solve for r. Plug it in. Francisco Rodríguez Henríquez

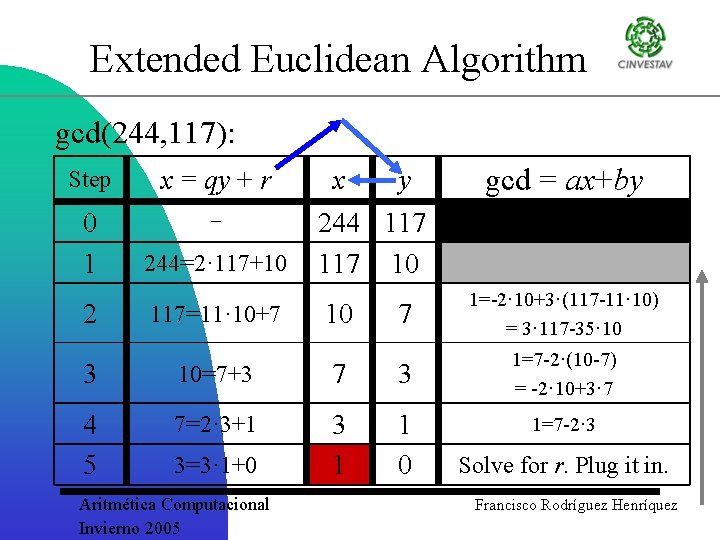
Extended Euclidean Algorithm gcd(244, 117): Step x = qy + r 0 1 - 2 244=2· 117+10 117=11· 10+7 x y 244 117 10 10 7 1=-2· 10+3·(117 -11· 10) = 3· 117 -35· 10 1=7 -2·(10 -7) = -2· 10+3· 7 3 10=7+3 7 3 4 5 7=2· 3+1 3 1 1 0 3=3· 1+0 Aritmética Computacional Invierno 2005 gcd = ax+by 1=7 -2· 3 Solve for r. Plug it in. Francisco Rodríguez Henríquez

Extended Euclidean Algorithm gcd(244, 117): Step x = qy + r 0 - 1 2 3 244=2· 117+10 117=11· 10+7 10=7+3 7=2· 3+1 4 3=3· 1+0 5 Aritmética Computacional Invierno 2005 x y gcd = ax+by 244 117 10 1= 3· 117 -35·(244 - 2· 117) = -35· 244+73· 117 7 1=-2· 10+3·(117 -11· 10) = 3· 117 -35· 10 7 3 1=7 -2·(10 -7) = -2· 10+3· 7 3 1 1 0 10 1=7 -2· 3 Solve for. Rodríguez r. Plug. Henríquez it in. Francisco

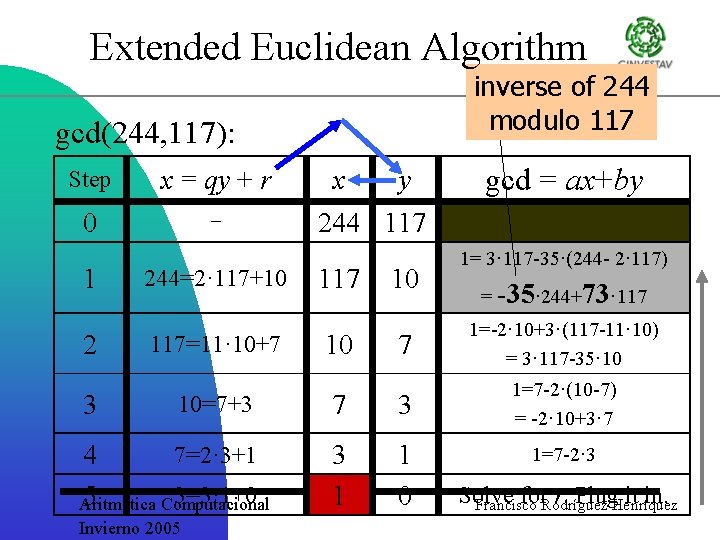
Extended Euclidean Algorithm inverse of 244 modulo 117 gcd(244, 117): Step x = qy + r 0 - 1 2 3 244=2· 117+10 117=11· 10+7 10=7+3 7=2· 3+1 4 3=3· 1+0 5 Aritmética Computacional Invierno 2005 x y gcd = ax+by 244 117 10 1= 3· 117 -35·(244 - 2· 117) = -35· 244+73· 117 7 1=-2· 10+3·(117 -11· 10) = 3· 117 -35· 10 7 3 1=7 -2·(10 -7) = -2· 10+3· 7 3 1 1 0 10 1=7 -2· 3 Solve for. Rodríguez r. Plug. Henríquez it in. Francisco

Extended Euclidean Algorithm Summary: Extended Euclidean algorithm works by keeping track of how remainder r results from dividing x by y. Last such equation gives gcd in terms of last x and y. By repeatedly inserting r into the last equation, one can get the gcd in terms of bigger and bigger values of x, y until at the very top is reached, which gives the gcd in terms of the inputs a, b. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Extended Euclidean Algorithm Input two positive integers a and b with a ≥ b. Output d = gcd(a, b) and integers x, y satisfying ax+by =d. 1. if (b = 0) { d = a; x = 1; y = 0; Fact: This algorithm has a Running time of O((lg n)2) return(d, x, y); bit operations. } 2. x 2 = 1; x 1 = 0; y 2 = 0; y 1 = 1. 3. while (b >0) { } 4. d = a; x = x 2; y = y 2; return(d, x, y); Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

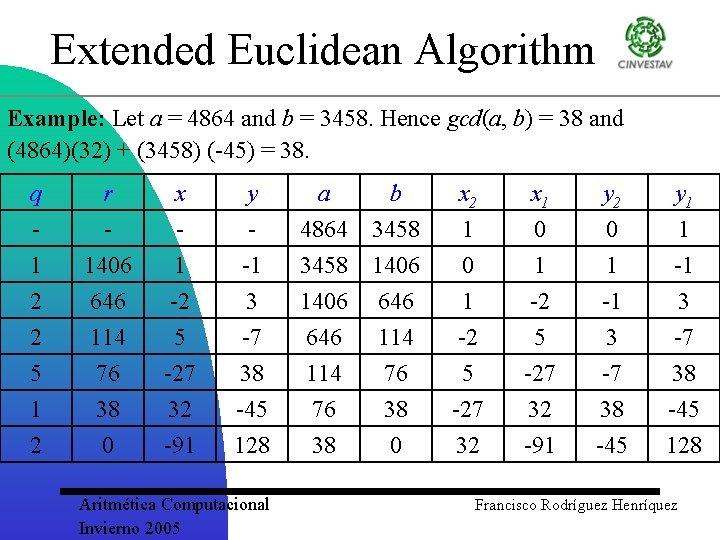
Extended Euclidean Algorithm Example: Let a = 4864 and b = 3458. Hence gcd(a, b) = 38 and (4864)(32) + (3458) (-45) = 38. q 1 2 r 1406 646 x 1 -2 y -1 3 2 5 1 2 114 76 38 0 5 -27 32 -91 -7 38 -45 128 Aritmética Computacional Invierno 2005 a b 4864 3458 1406 646 x 2 1 0 1 x 1 0 1 -2 y 2 0 1 -1 y 1 1 -1 3 646 114 76 38 -2 5 -27 32 -91 3 -7 38 -45 128 114 76 38 0 Francisco Rodríguez Henríquez

Quizz !! 1. Prove that there an infinite number of prime numbers. 2. Prove that e has an inverse modulo N if and only if e and N are relatively prime. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Finite fields: definitions and operations FP finite field operations : Addition, Squaring, multiplication and inversion Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

What is a Group? An Abelian group <G, +> is an abstract mathematical object consisting of a set G together with an operation * defined on pairs of elements of G, here denoted by +: In order to qualify as an Abelian group, the operation has to fulfill the following conditions: i. Closed: ii. Associative: iii. Commutative: iv. Neutral element: v. Inverse elements: Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

What is a Group? • Example: The best-known example of an Abelian Group is <Z, +> • Example: The additive group Z 15 uses the integers from 0 to 14. Some examples of additions in Z 15 are: (10 + 12) mod 15 = 22 mod 15 = 7 • In Z 15, 10 + 12 = 7 and 4 + 11 = 0. Notice that both calculations have answers between 0 and 14. • Additive Inverses – Each number x in an additive group has an additive inverse element in the group; that is an integer -x such that x + (-x) = 0 in the group. In Z 15, -4 =11 since (4 + 11) mod 15 = 15 mod 15 = 0. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Rings (1/2) 1. 2. 3. 4. A ring <R, +, *> consists of a set R with 2 operations defined on its elements, here denoted by + and *. In order to qualify as a ring, the operations have to fulfill the following conditions: The structure <R, +> is an Abelian group. The operations * is closed, and associative over R. There is a neutral element for * in R. The two operations + and * are related by the law of distributivity: A ring <R, +. *> is called a commutative ring if the operation * is commutative. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Rings (2/2) • The integer numbers, the rational numbers, the real numbers and the complex numbers are all rings. • An element x of a ring is said to be invertible if x has a multiplicative inverse in R, that is, if there is a unique such that: • 1 is called the unit element of the ring. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

What is a Field? • A structure <F, +, *> is called a field if F is a ring in which the multiplication is commutative and every element except 0 has a multiplicative inverse. We can define the field F with respect to the addition and the multiplication if: F is a commutative group with respect to the addition. • is a commutative group with respect to the multiplication. The distributive laws mentioned for rings, hold. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

What is a Field? • A field is a set of elements with two custom-defined arithmetic operations: most commonly, addition and multiplication. The elements of the field are an additive abelian group, and the non-zero elements of the field are a multiplicative abelian group. This means that all elements of the field have an additive inverse, and all non-zero elements have a multiplicative inverse. • A field is called finite if it has a finite number of elements. The most commonly used finite fields in cryptography are the field Fp (where p is a prime number) and the field F 2 m. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Finite Fields • A finite field or Galois field denoted by GF(q=pn), is a field with characteristic p, and a number q of elements. As we have seen, such a finite field exists for every prime p and positive integer n, and contains a subfield having p elements. This subfield is called ground field of the original field. • For the rest of this class, we will consider only the two most used cases in cryptography: q=p, with p a prime and q=2 m. The former case, GF(p), is denoted as the prime field, whereas the latter, GF(2 m), is known as the finite field of characteristic two or simply binary field. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Finite Fields • A finite field is a field with a finite number of elements. The number of elements in a finite field is called the order of the field. Fields of the same order are isomorphic: they display exactly the same algebraic structure differing only in the representation of the elements. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

The field Fp • The finite field Fp (p a prime number) consists of the numbers from 0 to p 1. Its operations are addition and multiplication. All calculations must be reduced modulo p. • It is mandatory to select p as a prime number in order to guarantee that all the non-zero elements of the field have a multiplicative inverse. • Other operations in Fp (such as division, subtraction and exponentiation) can be derived from the definitions of addition and multiplication. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

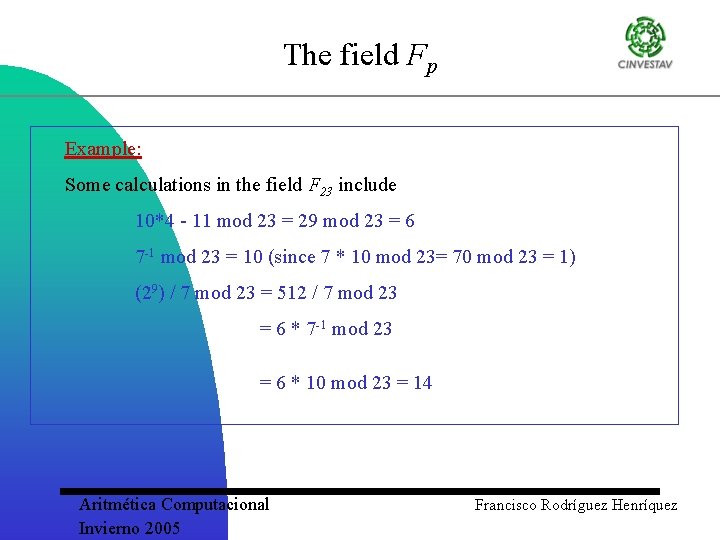
The field Fp Example: Some calculations in the field F 23 include 10*4 - 11 mod 23 = 29 mod 23 = 6 7 -1 mod 23 = 10 (since 7 * 10 mod 23= 70 mod 23 = 1) (29) / 7 mod 23 = 512 / 7 mod 23 = 6 * 7 -1 mod 23 = 6 * 10 mod 23 = 14 Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Congruences Definition: Let a, b, n be integers with n ≠ 0. We say that , (read: a is congruent to b mod n). If (a-b) is a multiple (positive or negative) of n, i. e. , a = b + nk, for some integer k. Examples: 32=7 mod 5, -12 = 37 mod 7. Proposition: Let a, b, c, d, n be integers with n ≠ 0. i. iii. iv. a = 0 mod n iff n|a. a = a mod n; a = b mod n iff a = b mod n. If a = b mod n and b = c mod n, then a = c mod n. a = b mod n and c = d mod n. Then a ± c = b ± d mod n, ac = bd mod n Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Fermat’s Petit Theorem: Let p be a prime. i. ii. If In other words, when working modulo a prime p, exponents can be reduced modulo p-1. iii. In particular Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Euler Theorem: Let n ≥ 2 be an integer. Then, If n is a product of distinct primes, and if In other words, when working modulo such an n, exponents can be reduced modulo (n). A special case of Euler’s theorem is Fermat’s petit theorem. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Euler and Fermat’s theorems examples Examples: 1. What are the last three digits of 7803 Equivalent to work mod 1000 (why? ). Since (1000)=1000(1 -1/2)(1 -1/5)=400, we have 7803 = (7400)273=(1) 273=73=343 mod 1000. (why? ) 2. Compute 23456 mod 5. From Fermat’s petit theorem we know that 24=1 mod 5. Therefore, 23456 = (24)864 = (1) 864 = 1 mod 5 Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

The order of an element in the field Fp The order of an element in F, is defined as the smallest positive integer k such that k=1 mod p. Any finite field always contains at least one element, called a primitive element, which has order p-1. From Euler’s theorem we know that for any element in F, Using the above result, one can easily prove that the order of any element in F must divide (p)=p-1, i. e. , ord ( )| (p)= ord ( )| p-1. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Primitive Elements: how many? Fact: Suppose that is a primitive element in F. Then b = i mod n is also a primitive element in F iff gcd(i, (n))=1. It follows that the number of primitive elements in F is ¿Cuál es el otro? ( (n)). Example: Consider the powers of 3 mod 7: 31=3; 32=2; 33=6; 34=4; 35=5; 36=1. There are ( (7)) = 2 primitive elements in F 7 Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Chinese Remainder Theorem Fairy Tale: Chinese Emperor used to count his army by giving a series of tasks. 1. All troops should form groups of 3. Report back the number of soldiers that were not able to do this. 2. Now form groups of 5. Report back. 3. Now form groups of 7. Report back. 4. Etc. At the end, if product of all group numbers is sufficiently large, can ingeniously figure out how many troops. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Chinese Remainder Theorem Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Chinese Remainder Theorem mod 3: N mod 3 = 1 Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Chinese Remainder Theorem mod 5: N mod 5 = 2 Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Chinese Remainder Theorem mod 7: N mod 7 = 2 Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Chinese Remainder Theorem Secret inversion formula (for N < 105 = 3· 5· 7): N a (mod 3) N b (mod 5) N c (mod 7) Implies that N = (-35 a + 21 b + 15 c) mod 105. So in our case a = 1, b = 2, c = 2 gives: N = (-35· 1 + 21· 2 + 15· 2) mod 105 = (-35 + 42 + 30) mod 105 = 37 Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Chinese Remainder Theorem How can we find the secret formula? For any x, a, b, and c satisfying x a (mod 3) x b (mod 5) x c (mod 7) Chinese Remainder Theorem says that this is enough information to uniquely determine x modulo 3· 5· 7. Proof, gives an algorithm for finding x –i. e. the secret formula. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Chinese Remainder Theorem: Suppose that gcd(m, n) = 1. Given a and b, there exists exactly one solution x (mod mn) to the simultaneous congruences Proof [sketch]: There exist integers s, t such that ms+nt=1 (why? ). Then ms=1 mod n and nt =1 mod m (why? ). Let x = bms +ant. Then, Suppose x 1 is another solution, then c = (x-x 1) is a multiple of both, m and n (why? ). But then provided that m and n are relatively primes then c is also a multiple of mn. Hence, any two solutions x to the system of congruences are congruent mon mn as claimed. Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez

Chinese Remainder Theorem THM (CRT): Let m 1, m 2, … , mn be pairwise relatively prime positive integers. Then there is a unique solution x in [0, m 1·m 2···mn-1] to the system of congruences: x a 1 (mod m 1 ) x a 2 (mod m 2 ) x an (mod mn ) Aritmética Computacional Invierno 2005 Francisco Rodríguez Henríquez