Recurso Curso de Introduo Lgica Computacional Exerccio da

Recursão Curso de Introdução à Lógica Computacional

Exercício da aula passada de indução • Exercício 7: Prove qualquer postagem de correio de 12 centavos ou mais pode ser formado por conjunto de selos de 4 centavos e 5 centavos • 12 centavos= 3 selos de 4 c e 0 selos de 5 cents • 13 centavos= 2 selos de 4 c e 1 selos de 5 cents • 14 centavos= 1 selos de 4 c e 2 selos de 5 cents • 15 centavos= 0 selos de 4 c e 3 selos de 5 cents • 16 centavos= 4 selos de 4 c e 0 selos de 5 cents

Exercício da aula passada de indução • Exercício 7: Prove qualquer postagem de correio de 12 centavos ou mais pode ser formado por conjunto de selos de 4 centavos e 5 centavos • • P(n) s= (Q-R)*4 + R*5 (Q-R) é o numero de selos de 4 cents e R é o numero de selos de 5 cents Q=quociente(M/4) R= resto(M/4) - no Excel resto de uma divisao é MOD para n>=12

Exercício da aula passada de indução • Exercício 7: Prove qualquer postagem de correio de 12 centavos ou mais pode ser formado por conjunto de selos de 4 centavos e 5 centavos • P(n) s=[quociente(n/12) - resto(n/12) ]*selos de 4 cents & [ resto(n/12)] selos de 5 cents para n>=12

Prove: P(n) s=[quociente(n/12) - resto(n/12) ]*selos de 4 cents & [ resto(n/12)] selos de 5 cents para n>=12 • Passo indutivo: • Assuma • P(k) = [quociente(k/4) –resto(k/4)] * selos de 4 c & [resto(k/4)] *selos de 5 c • P(k+1)=P(k)+P(1)= [quociente(k+1)/4 )–resto((k+1)/4)] * selos de 4 c & [resto(k+1/4)] *selos de 5 c • [Quociente(k/4+¼)-resto(k/4+¼)]*selos de 4 cents + resto(k/4 + ¼))*selos de 5 cents • [Quociente(k/4)+quociente(1/4) –resto(k/4) –resto(¼)]*selos de 4 cents + [resto(k/4) +resto(¼)] * selos de 5 cents • [Quociente(k/4)– resto(k/4) ]* selos de 4 cents +[quociente(1/4)– resto(¼)]*selos de 4 cents + resto(k/4) * selos de 5 cents + resto(¼)] * selos de 5 cents • [Quociente(k/4)– resto(k/4) ]* selos de 4 cents + resto(k/4) * selos de 5 cents + [quociente(1/4)–resto(¼)]*selos de 4 cents + resto(¼)] * selos de 5 cents

Prove: P(n) s=[quociente(n/12) - resto(n/12) ]*selos de 4 cents & [ resto(n/12)] selos de 5 cents para n>=12 • Passo indutivo: • Assuma • P(k) = [quociente(k/4) –resto(k/4)] * selos de 4 c & [resto(k/4)] *selos de 5 c • P(k+1)=P(k)+P(1)= [quociente(k+1)/4 )–resto((k+1)/4)] * selos de 4 c & [resto(k+1/4)] *selos de 5 c • [Quociente(k/4+¼)-resto(k/4+¼)]*selos de 4 cents + resto(k/4 + ¼))*selos de 5 cents • [Quociente(k/4)+quociente(1/4) –resto(k/4) –resto(¼)]*selos de 4 cents + [resto(k/4) +resto(¼)] * selos de 5 cents • [Quociente(k/4)– resto(k/4) ]* selos de 4 cents +[quociente(1/4)– resto(¼)]*selos de 4 cents + resto(k/4) * selos de 5 cents + resto(¼)] * selos de 5 cents • [Quociente(k/4)– resto(k/4) ]* selos de 4 cents + resto(k/4) * selos de 5 cents + [quociente(1/4)–resto(¼)]*selos de 4 cents + resto(¼)] * selos de 5 cents

Recursão

Recursão • Conceito próximo ao de indução e presente na grande maioria das linguagens de programação O conceito e usado: • Na definição de sequências, funções e conjuntos; • Na implementação de algoritmos. Uma função P cujo domínio e o conjunto Z+ pode ser definida recursivamente através de dois passos: Passo 1) Especificar o valor de P(1); Passo 2) Dar um regra (relação de recorrência) para encontrar seu valor para um inteiro a partir de seu valor para inteiros menores. Tal definição e chamada de definição recursiva ou definição indutiva

Induc a o × Recursa o • Qualquer definição indutiva pode ser simulada por recursão • Nem toda recursão possui uma correspondente definição indutiva ∗ não necessariamente respeita a boa ordem da indução • recomendável programar recursão respeitando os princípios da definição indutiva ∗ garante que o programa para e atinge o resultado esperado

Recursividade Fundamental em Matemática e Ciência da Computação Um programa recursivo e um programa que chama a si mesmo Uma função recursiva e definida em termos dela mesma Exemplos Números naturais, Função fatorial, Árvore Conceito poderoso Define conjuntos infinitos comandos finitos

Tipos de Recursão recursão direta: a função A chama a própria função A recursão indireta: função A chama uma função B que, por sua vez, chama A

Condição de parada Nenhum programa nem func a o pode ser exclusivamente definido por si Um programa seria um loop infinito Uma func a o teria definic a o circular Condic a o de parada Permite que o procedimento pare de se executar F(x) > 0 onde x e decrescente

Recursividade • A recursividade e uma estratégia que pode ser utilizada sempre que o cálculo de uma função para o valor n, pode ser descrita a partir do cálculo desta mesma função para o termo anterior (n-1). • Exemplo – Função fatorial:

Definição Indutiva – exemplo--Fatorial logo: n! = n * (n-1)!

Prova

Programação recursiva PASCAL LISP

Eficiência da Recursão

Eficiência da Recursão • Recursão em Linguagens funcionais, como LISP • técnica padrão de aplicar uma operação sucessivamente • base da maioria dos programas funcionais • Otimizações na o-usadas em linguagens imperativas estudo de tais técnica na o e detalhado

Recursão – execução • Para cada chamada de uma func a o, recursiva ou na o, os para metros e as varia veis locais sa o empilhados na pilha de execuc a o.

Recursão -- Execução Internamente, quando qualquer chamada de func a o e feita dentro de um programa, e criado um Registro de Ativac a o na Pilha de Execuc a o do programa O registro de ativac a o armazena os para metros e varia veis locais da func a o bem como o “ponto de retorno” no programa ou subprograma que chamou essa func a o. Ao final da execuc a o dessa func a o, o registro e desempilhado e a execuc a o volta ao subprograma que chamou a func a o

Exemplo: FATORIAL

Complexidade • A complexidade de tempo do fatorial recursivo e O(n). (Em breve iremos ver a maneira de calcular isso usando equac o es de recorre ncia) • Mas a complexidade de espac o tambe m e O(n), devido a pilha de execuc a o • Ja no fatorial na o recursivo a complexidade de espac o e O(1) Portanto, a recursividade nem sempre e a melhor soluc a o, mesmo quando a definic a o matema tica do problema e feita em termos recursivos

Outro exemplo: Fibonacci

Fibonacci não recursivo • Complexidade: O(n) Conclusa o: na o usar recursividade cegamente!

Quando vale a pena usar recursividade • Em Algoritmos complexos, cuja a implementac a o iterativa e complexa e normalmente requer o uso expli cito de uma pilha • Dividir para Conquistar (Ex. Quicksort) • Caminhamento em A rvores (pesquisa, backtracking)

Dividir para Conquistar • Duas chamadas recursivas Cada uma resolvendo a metade do problema • Muito usado na pra tica Soluc a o eficiente de problemas Decomposic a o • Na o se reduz trivialmente como fatorial Duas chamadas recursivas • Na o produz recomputac a o excessiva como fibonacci • Porc o es diferentes do problema

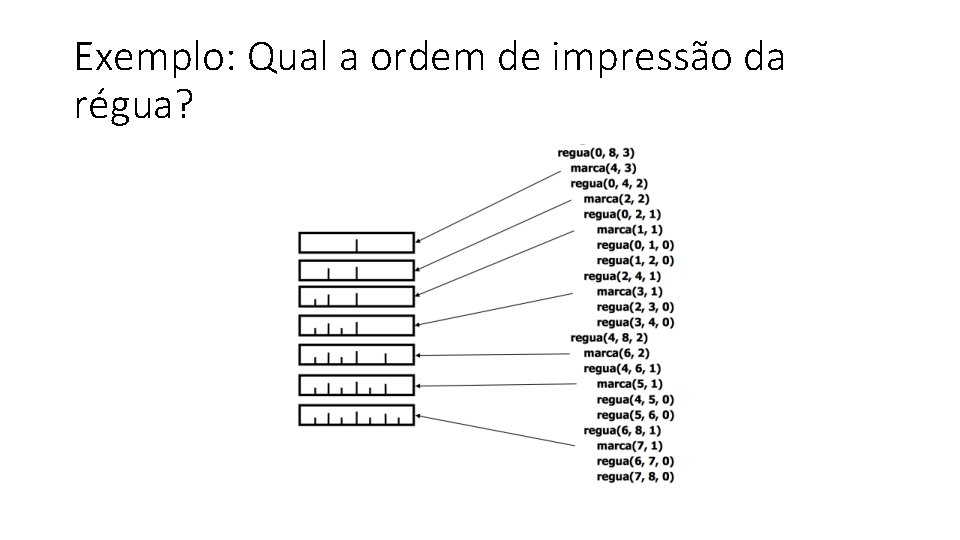
Exemplo: Qual a ordem de impressão da régua?

Exemplo: Qual a ordem de impressão da régua?

Outra implementação para a régua

Análise da função Fatorial • Qual a equac a o de recorre ncia que descreve a complexidade da func a o fatorial? • T(n) = 1 + T(n-1) T(1) = 1 • T(n) = 1 + T(n-1) = 1 + T(n-2) = 1 + T(n-3). . . • T(2) = 1 + T(1)

Exercicio • Crie uma func a o recursiva que calcula a pote ncia de um nu mero: • Como escrever a func a o para o termo n em func a o do termo anterior? • Qual a condic a o de parada?

Exercicio • Implemente uma func a o recursiva para computar o valor de 2 n

Exercício: Determinar o valor de um elemento máximo de um vetor v[0. . n-1] n ≥ 1 Solução Iterativa Solução Recursiva

• A função maximo. R aplica a recursão ao segmento v[0. . n-2] do vetor.

Análise de correção da função recursiva • A análise da correção do algoritmo tem a mesma forma que uma prova por indução. • Se n vale 1 então v[0] é o único elemento relevante do vetor e portanto v[0] é o máximo. • Agora suponha que n vale mais que 1. Então nosso vetor tem duas partes: v[0. . n-2] e v[n-1] portanto o valor que procuramos é o maior dentre

Outra forma de calcular o valor máximo de um vetor A função maximo 2 é apenas uma embalagem ou invólucro (= wrapper-function); o serviço pesado é executado pela função recursiva max. R: max. R resolve um problema mais geral que o original. A necessidade de generalizar o problema original ocorre com frequência no projeto de algoritmos recursivos.

• Qual o valor de X (4) se X é dada pelo seguinte código? int X (int n) { if (n == 1 or n == 2) return n; else return X (n-1) + n * X (n-2); }

Exercício: Soma dos n primeiros números naturais, agora com função recursiva: • A soma de n números é igual a somar n com a soma de todos os anteriores a n; • Matematicamente, a soma é n + S(n - 1); • Mas a soma S(n - 1) por sua vez, recorrendo a ela própria, é S(S(n - 1); • Até onde isso continua? Até S(1) ou S(0), não há mais para onde ir, a soma é igual a ela própria nesses casos.

Erros comuns • Confundir iteração com recursão; • Confundir uma função que chama a si mesma com chamar a função com si própria como argumento; • Recursão infinita ou excessiva.

• Muitos problemas têm a seguinte propriedade: cada instância do problema contém uma instância menor do mesmo problema. Dizemos que esses problemas têm estrutura recursiva. Para resolver um tal problema, podemos aplicar o seguinte método: • se a instância em questão for pequena, resolva-a diretamente (use força bruta se necessário); • senão, reduza-a a uma instância menor do mesmo problema, • aplique o método à instância menor, • volte à instância original. • A aplicação desse método produz um algoritmo recursivo. Para mostrar como isso funciona, examinaremos um exemplo concreto. •

Recursividade O que e recursão? – E um método de programação no qual uma função pode chamar a si mesma – O termo e usado de maneira mais geral para descrever o processo de repetição de um objeto de um jeito similar ao que ja fora mostrado

Por que precisamos aprender recursão? – Paradigma de programação poderoso – Nova maneira de pensar Muitas estruturas têm natureza recursiva: – Estruturas encadeadas – Fatorial, máximo divisor comum – Uma pasta que contém outras pastas e arquivos