Complexidade Computacional e Jogos Jan2004 Teoria de Complexidade

Complexidade Computacional e Jogos Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Agenda da Apresentação -Preliminares de Teoria da Computação e Complexidade Computacional - Aspectos Computacionais de Jogos - Teoria dos Jogos desde o Teorema de Zermelo Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

- O que é a (Teoria da) Computação ? (Tentativa de) conceituação do Computável - O que é Lógica ? (Tentativa de) conceituação do Razoável TECMF

Computável Toda tarefa que pode ser realizada por um ser burro com um mínimo de conhecimento/capacidade. burro = Incapaz de Aprender conhecimento = ? Máquina de Raciocinar (Leibniz 1667) Antes de 1900 d. c ====> Máquina de Calcular de Pascal. (Pascal sec. XVII) Máquina de Babbage (Ch. Babbage. sec. XIX) TECMF

Razoável Todo evento que é passível de uma explicação, na forma argumentativa, construída sobre fatos iniciais inquestionáveis. Antes de 1879 Lógica Aristotélica e Escolástica (a partir de 300 a. c. ) ====> Álgebras Booleanas (Boole 1847) Álgebra Relacional (De. Morgan, Schroeder, C. S. Peirce XIX) TECMF

Panorama da Matemática no Século XIX - Problemas da Física Matemática (Sec. XVIII-XIX): - Equação da Onda - Equação do Calor - Equação de Poisson - Técnicas de Fourier - Séries Infinitas são usadas na solução de Eq. Dif. Parciais - Problemas de Fundamentação: - Séries divergentes x Séries Convergentes - Conceito de infinito não era preciso - Conceito de função não era preciso - O próprio conceito de número real não era preciso. - Definição de convergência não existia Necessidade de teoria mais abrangente e abstrata Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Panorama da Matemática no Século XIX (cont. ) Dedekind (1831 -1916) Estabelece o princípio de indução e define conceito de número real Cauchy (1789 -1857) Bolzano(1781 -1848) Aritmetização da Análise, definição dos conceitos de limite, funções e funções contínuas, convergência de sequências e séries infinitas Riemman(1826 -1866) Definição do conceito de integral e Teorema Fundamental do Cálculo. Geometrias Não-Euclidianas Peano (em 1889) Define os axiomas da aritmética Weierstrass (1815 -1897) Estabelece critérios para a diferenciação e integração, termo a termo, de séries infinitas Hilbert (em 1898 -1899) Estabelece a fundamentação da geometria Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Teoria Ingênua dos Conjuntos Bolzano concebe a noção (abstrata) de conjuntos (finitos e infinitos) Cantor (de 1867 a 1871) define a teoria de conjuntos e prova a existência de conjuntos infinitos com cardinalidades diferentes. Conceitos de números cardinais e ordinais transfinitos. Resistência aos principais resultados em função do “receio do infinito” Alguns paradoxos: - Burali-Forti (1897) “Não há o ordinal de todos os ordinais” - Russell (1902) “Não há o conjunto de todos os conjuntos” R = { x / x x} Jan/2004 ==> R R se e somente se R R Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Evolução da Lógica como assunto matemático De. Morgan (1830) Observa que a álgebra não necessita lidar tão somente com conceitos numéricos. Boole (1854) Descreve uma álgebra a partir de operações entre conjuntos e relações lógicas, confirmando De. Morgan. Frege (1879) estabele a lógica como um sistema formal que tem sua linguagem particular e distinta da natural. O conceito de prova matemática passa a ser formal. Frege (1884) busca a fundamentação da aritmética em bases puramente lógicas , com a adição do conceito de pertinência ( ) como primitivo. ===> Os paradoxos aparecem novamente !! ===> Paradoxos associados ao axioma da escolha Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

As 3 Abordagens para a Fundamentação da Matemática Logicismo (Frege) - Toda a Matemática é consequência de princípios puramente lógicos. Formalismo (Hilbert) - A Matemática é fundamentada por sistemas formais cujo único requisito é a consistência Intuicionismo (Brouwer) - A Matemática é uma atividade humana fundamentada em processos construtivos, sendo assim todo objeto matemático tem sua existência expressa por construção. Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

O Programa de Hilbert => Obtenção de uma prova da consistência da matemática, observando-se que: - As teorias mais complexas são extensões das mais simples. Th(N) Th(Z) Th(Q) Th(R) Th(C) - Tais extensões são, na sua maior parte, obtidas por operações básicas (classes de equivalência, completamento por simetria, por compactação, completamento algébrico, etc) => Prova da consistência da Aritmética ( Th(N)) com o uso de técnicas finitárias. => Provar que não existe prova de 0 = 1 usando. . . Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

A Computação do ponto de vista das funções prim. recursivas 1931 - Gödel define as funções prim. recursivas associando-as a provas em aritmética 1927/1928 - Ackermann define uma função que necessita de recursão simultânea 1934 - Rózsa Péter - Prova que as funções prim. recursivas formam a classe definida por recursão simples e “nested” a partir de funções iniciais constantes, identidade e a função sucessor. Prova que a função de Ackermann é na realidade definida por recursão em duas variáveis e não é portanto primitivamente recursiva, mas é computável. 1936 - A. Turing - Define uma máquina formal a partir de princípios simples (ler , apagar e escrever símbolos em uma fita) e define o conceito de Máquina Universal. Prova que não existe máquina capaz de verificar se outra máquina pára ou não. Desde o início a sua máquina com versão Não-Determinística 1936 - A. Church Define o -Calculus e mostra que este é capaz de definir todas as funções para as quais existe uma Máquina de Turing. 1936 - Kleene Define, aceitando que o computável inclui a parcialidade funcional, as funções parcialmente recursivas e lança a Tese de Church. 1947 - Markov Estabele o conceito de computável com base em identificação de palavras e símbolos (algoritmos de Markov) e justifica o ponto de vista finitista da computação. Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Sxyz (xz)yz : 0: I : 1: P 0 K Kxy x Ix x (I SKK) : 2: P 1 K. . . : n: P: n-1: K. . P Tese de Church: f: N N é computável se e somente se existe um combinador F C 1 C 2. . . Ck tal que para todo n N (F: n: : m: ) f(n) = m) fé recursiva n existe uma máquina de Turing M , tal que M com 11. . . . 111 na fita de entrada M pára com 11. . . 11111 na saída sssnf(n) = m existe um algoritmo de Markov A , mt. q. A lendo 11. . . . 111 pára e produz o string 11. . . 11111 na saída sss f(n) = m m Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

A Tese de Church é um enunciado científico, portanto não possui demonstração matemática. Evidência Forte para a Tese de Church Teorema de Rogers (1958): Sejam duas FAA’s ( i)i N então existe f recursiva e bijetiva tal que i = f(i) Obs: Uma FAA é um conjunto de funções parciais ( i)i N, tal que: 1 - As funções parc. recursivas estão todas em ( i)i N 2 - Existe u N com u parc. recursiva tal que para todo i e x u(i, x) = i(x) 3 - Existe c recursiva tal que c(i, j) = i j Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Medindo a eficiência de algoritmos - Escolha do modelo computacional - Recursos: Tempo , Memória - Relacionando os algoritmos e os problemas que estes resolvem - Computação de Funções - Problemas de otimização - Problemas de decisão, - Linguagens -Classes de complexidade: Classificando problemas pela complexidade do algoritmo mais eficiente que o resolve. Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Satisfação na Lógica Proposicional “Dada uma fórmula da lógica proposicional, isto é, formada com os conectivos , , e , deseja-se saber se existe uma valoração que a satisfaça” Problema SAT Solução: Gerar todas as valorações e testar uma até encontrar. Se não encontrar ao final do teste de todas as valorações informar que a fórmula não é satisfatível. Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

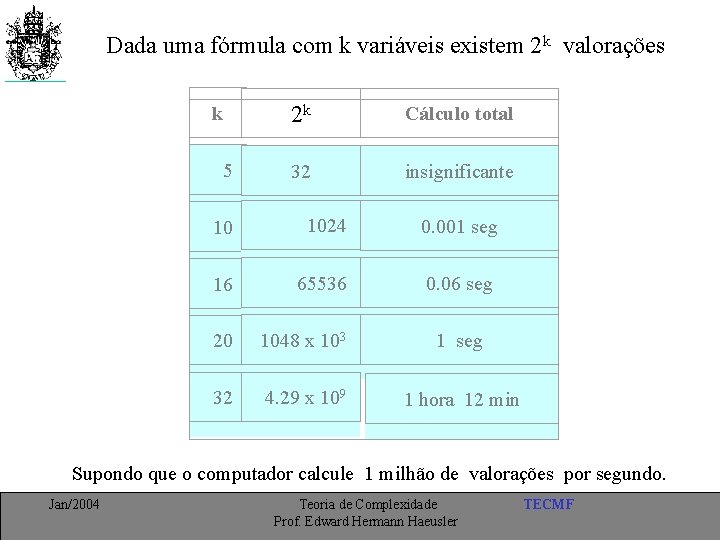
Dada uma fórmula com k variáveis existem 2 k valorações k 5 2 k Cálculo total 32 insignificante 10 1024 0. 001 seg 16 65536 0. 06 seg 20 1048 x 103 1 seg 32 4. 29 x 109 1 hora 12 min Supondo que o computador calcule 1 milhão de valorações por segundo. Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Por outro lado ……… -Verificar se uma valoração satisfaz uma fórmula é muito rápido (muito menos que 1 x 10 -7 seg) para fórmulas com até 100 variáveis em um pentium IV 1 GHz. -Dada uma valoração, avaliar o valor da fórmula leva no máximo k operações, onde k é o tamanho da fórmula. Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

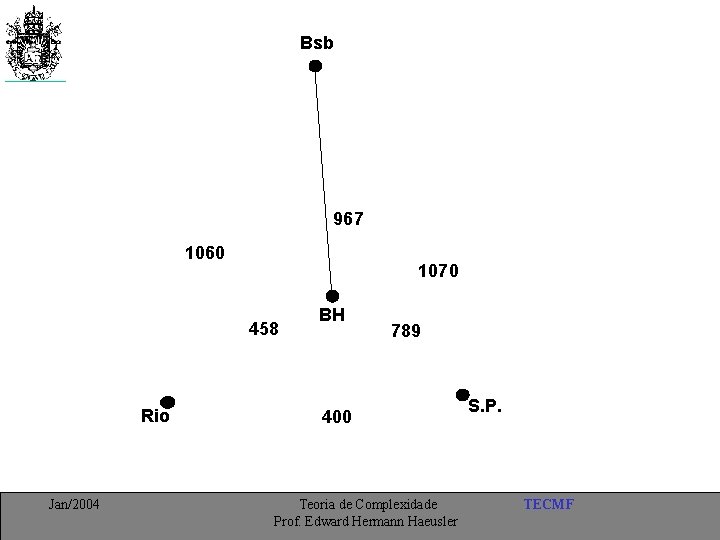
O problema do Caixeiro Viajante “Suponha que um caixeiro viajante tenha que visitar k cidades diferentes, iniciando e encerrando esta viagem na primeira cidade. Não importa a ordem com que as cidades são visitadas. Sabe-se que de cada cidade pode-se ir diretamente a qualquer outra. O problema do caixeiro viajante consiste em descobrir a rota que torna mínima a viagem total (em kms)”. Obs: Tal rota é dita ser um ciclo hamiltoniano no grafo. Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Bsb 967 1060 1070 458 Rio Jan/2004 BH 789 400 Teoria de Complexidade Prof. Edward Hermann Haeusler S. P. TECMF

O problema do caixeiro viajante é um problema de otimização combinatória. (a) Podemos transforma-lo num problema de enumeração ? (b) Podemos determinar todas as rotas do caixeiro ? (c) Podemos saber qual delas é a menor ? SOLUÇÃO: São (k-1)! Rotas É um trabalho fácil para a máquina ? Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

( k - 1 )! cresce muito rápido k 5 (k - 1)! Cálculo total 24 insignificante 10 362 880 15 87 bilhões 24 hs e 6 min 20 1. 2 x 1017 3 milhões de anos 25 6. 2 x 1023 0. 19 x 1017 anos 0. 3 seg Supondo que o computador calcule 1 milhão de rotas por segundo. Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

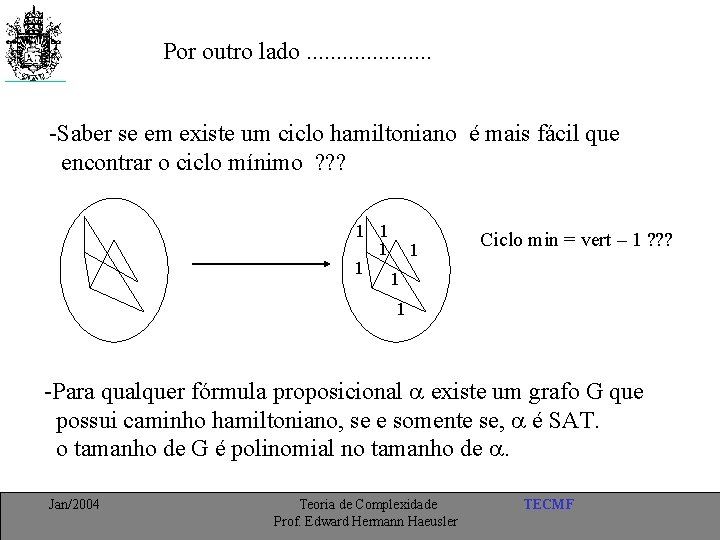
Por outro lado. . . . . -Saber se em existe um ciclo hamiltoniano é mais fácil que encontrar o ciclo mínimo ? ? ? 1 1 1 Ciclo min = vert – 1 ? ? ? 1 1 -Para qualquer fórmula proposicional existe um grafo G que possui caminho hamiltoniano, se e somente se, é SAT. o tamanho de G é polinomial no tamanho de . Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

SAT e as Máquinas de Turing não-determinísticas t w Si, j t Ee t Ci = Símbolo j na posição i no tempo t = Máquina está no Estado e no tempo t = Cabeça está no na posição i no tempo t Se SAT puder ser resolvido emdescrever: tempo polinomial Fórmulas para por uma M. T. deter então -A qualquer problema em NP também cabeça em qualquer tempo t está em uma e somente P(|w|) umaem posição pode ser resolvido tempo polinomial -Cada pósição da fita tem, em qualquer t, um e somente Um símbolo escrito. - A máquina, em qualquer tempo t, está em um e somente um estado Fórmulas para descrever o comportamento da máquina: t+1 t+1 t+1 Ete Cit Si, jt (Eg Ci+1 Si, k) (Eh Ci-1 Si, n ) Fórmulas para descrever o a conf. Inicial da fita: 0 0 S 0 . . . S 0, 3 S 1, 7 2, 1 |w|, 8 Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

(1) Descobrindo como resolver o problema do caixeiro viajante em tempo polinomial, seremos capazes de resolver, também em tempo polinomial, outros problemas importantes (úteis). (2) Se alguém provar que é impossível resolver o problema do caixeiro em tempo polinomial no número de cidades, também se terá que outros de problemas importantes não tem solução prática. (3) Costuma-se resumir essas propriedades do problema do caixeiro dizendo que ele pertence à categoria dos problemas NP - completos. Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

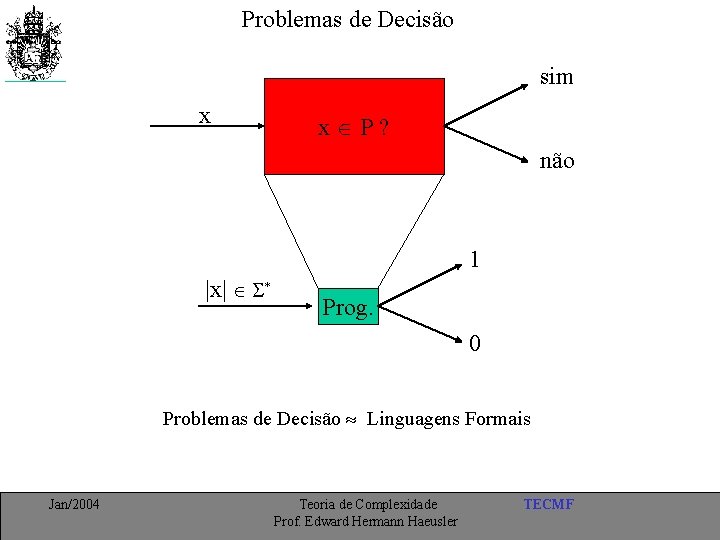
Problemas de Decisão sim x x P? não 1 |x| * Prog. 0 Problemas de Decisão Linguagens Formais Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Problemas, Soluções e Linguagens P = < Ent, Saída, Relação> * , Saída * , R> PComp = < Ent è Sol = f: Ent Saída f Relação * f: *Ent Saída è Sol. Comp = f computável f R * Saída * } LP = { went<sep>wsai / (went, wsai) R Ent Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Complexidade de uma Linguagem L DTime(f) sss m Turing. Det t. q. (m reconhece L) e c, x * steps(m, x) cf(|x|) L DSpace(f) sss m Turing. Det t. q. (m reconhece L) e c, x * space(m, x) cf(|x|) Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Uso de Recursos por Máquinas de Turing Determ. L * f : *1 *2 ML reconhece L sss w L então ML(w) = “aceita” w L então ML(w) = “rejeita” Mf computa f sss f(w 1)=w 2 então ML(w 1) = w 2 steps(M, w) = números de passos executados pela máquina M sobre o dado w até parar. space(M, w) = números de células (distintas) visitadas pela máquina M sobre o dado w até a parada. Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Por que considerar classes assintóticas de funções ? ? Teorema: (speedup linear) Se uma linguagem L é decidida em tempo f(n) então para qualquer > 0 existe uma M. Turing M que decide L em tempo . f(n) + n + 2. Prova : Modificar o tamanho da “palavra” de memória Consequências do seedup: Se L é decidida em tempo f(n) = 165. nk +. . + 54. n + 657 então L é decidida em tempo f’(n) = nk Obs: O mesmo teorema ( e técnica de prova) vale para função de medida e uso de espaço (número máximo de células visitadas) Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Complexidade Computacional I - Não existência de limite na complexidade de Linguagens DTime(f) Dtime(f log(f)) DSpace(f) DSpace(f log(f)) - Hierarquia de Linguagens segundo sua Complexidade DTime(n) Dtime(n 2) . . . Dtime(nk) . . Dtime(2 n). . . Dspace(log(n)) Dspace(n) . . . DSpace(nk) . . Dtime(2 n). . . Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Teorema de Cantor {A / A B} ==> Seja B um conjunto, então |B| < |2 B| Prova: Suponha que |B| = |2 B| então existe f: B 2 B S = { x / x f(x) } f-1(S) S se e somente se f-1(S) S Paradoxo do Barbeiro: Em uma cidade existe um barbeiro que faz a barba de todos os homens que não barbeiam a sí próprios e somente estes. Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

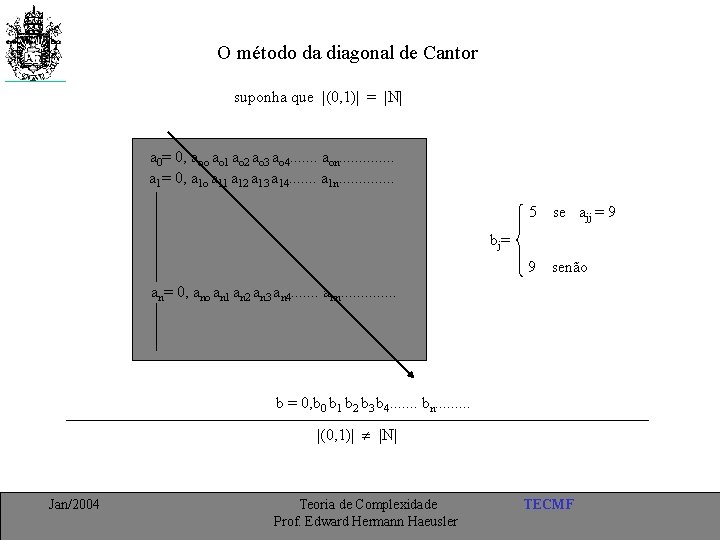
O método da diagonal de Cantor suponha que |(0, 1)| = |N| a 0= 0, aoo ao 1 ao 2 ao 3 ao 4. . . . aon. . . a 1= 0, a 1 o a 11 a 12 a 13 a 14. . . . a 1 n. . . 5 se ajj = 9 bj= 9 senão an= 0, ano an 1 an 2 an 3 an 4. . . . ann. . . b = 0, b 0 b 1 b 2 b 3 b 4. . . . bn. . |(0, 1)| |N| Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Hierarquia própria de funções construtivas Paraf = { <T, x> / T(x) pára no máximo em f(|x|) passos} Fato. I : Paraf DTime(f 3) Fato. II : Paraf DTime(f(x/2)) Prova: Diagonalização Corolário I : DTime(f(n)) DTime(f(2 n+1)3) Corolário II : P EXP Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Classes de Complexidade e algumas relações Def. PSpace = DSpace(ni) i N Def. NPSpace = NSpace(ni) i N Def. NP = NTime(ni ) i N Def. Log = Space(log(n)) Jan/2004 NLog = NSpace(log(n)) Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

- DSpace(f(n)) NSpace(f(n)) e DTime(f(n)) NTime(f(n)) - NTime(f(n)) DSpace(f(n)) - NSpace(f(n)) DTime(klog n + f(n)) (obs; Número de conf. + alcançabilidade) - Alcançabilidade Space(log 2) - número de nós alcançavel Space(log) => Jan/2004 NSpace(f) Space(f 2) NSpace(f) = co. NSpace(f) Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

(parte) do que se sabe atualmente (desde 60’s) Log NLog P NP PSPACE = NPSPACE EXP NEXP Sabe-se que Log PSPACE se P = NP então EXP = NEXP se Log = P então EXP = PSPACE Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

P : Encontra solução em tempo polinomial em MTD NP : Verifica solução em tempo polinomial em MTD Co. NP : Verifica que não é solução, em tempo polinomia em MTD Taut Co. NP Sat NP Verificação de Modelos Prova de Teoremas Obs: Se Co. NP então NP P Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Como SAT é NP-Completo então Taut é Co. NP-Completo ===> Se existe um sistema dedutivo onde todas as provas tem tamanho polinomial em função do tamanho da conclusão, então Co. NP = NP. Senão existe tal sistema então Co. NP e portanto NP P. ? NP é um problema genuinamente matemático. ===> P = ? ===> P = NP é um problema da ciência da computação. ? ===> P = NP é um problema genuinamente de fundamentação e lógica. - Já se tentou técnicas de construção de modelos via “forcing” (funcionou com a hipótese generalizada do continum) mas a crença geral é que não funciona. - Técnicas de diagonalização e relativização (tradição lógico-matemática) tem sido extensivamente usadas no estudo de questões relacionadas a NP=P. Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

O Maior problema atual em Teoria da Computação é : ? P = NP O que isto tem a ver com jogos ? ? ? - Jogos e “quebra-cabeças” : PSPACE, EXP e NP-completos -Soluções para jogos (Equilíbrio de Nash p. ex. ), estão em P? ? ? (estratégias mistas com soma zero), NP-completos (estratégias puras) e EXP ? (estratégias mistas para jogos em geral) Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Em Geral (versões infinitas) http: //www. ics. uci. edu/~eppstein/cgt/hard. html#refs Damas é EXP-completo Xadrez é EXP-completo Sokoban é PSPACE-completo Clickomania é NP-completo 15 -p é P (existência de solução) e NP-completo (melhor sol. ) ÞA Teoria de Complexidade adequada para o estudo das versões finitas é a Teoria de complexidade estrutural ou de Kolmogorov Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

O jogo de Geografia é PSPACE-completo èLógica Proposicional Intuicionista é PSPACE-completa (Statman 1977) Prova: A sentenças válidas intuicionisticamente podem ser caracterizadas como sendo aquelas que possuem estratégia vencedora para o jogador que começa o seu jogo dialógico. (Haeusler 2004) Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Conclusão Teoria dos Jogos Matemática Economia Complexidade Computacional Engenharia Fundamentação e Lógica Muito Obrigado pela audiência !!!! Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Um Pouco de História sobre Teoria dos Jogos e Xadrez 1 Zermelo 1913 – Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels 5 o Congresso de Matemáticos (Cambridge). König 1927 – Über eine Schulussweise aus dem Endlichen ins Unendliche. Acta Sci. Math. Kalmár 1928 – Zur Theorie der abstrakten Spiele. Acta Sci Math. Utiliza indução transfinita Caracterizam o conceito de posição ganhadora Von Neumann 1928 – Zur Theorie der Gesellschaftsspiele. Mathematische Annalen Caracteriza a interação entre as estratégias dos jogadores 1 - Jogo de Informação Perfeita Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

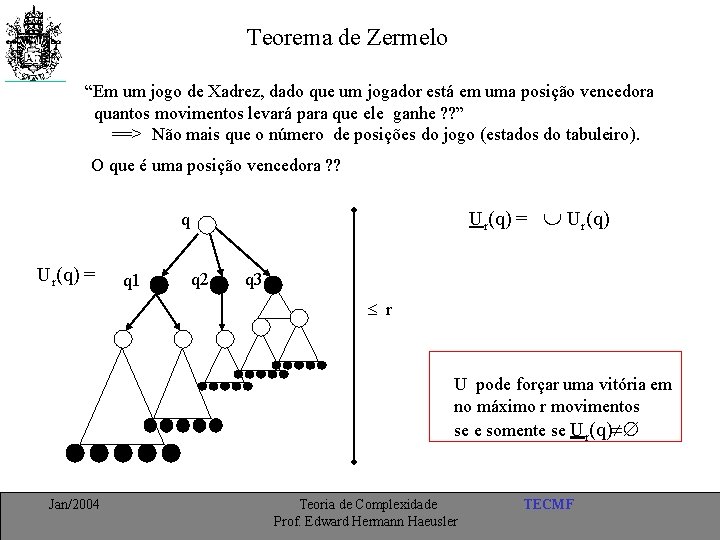
Teorema de Zermelo “Em um jogo de Xadrez, dado que um jogador está em uma posição vencedora quantos movimentos levará para que ele ganhe ? ? ” ==> Não mais que o número de posições do jogo (estados do tabuleiro). O que é uma posição vencedora ? ? Ur(q) = q 1 q 2 Ur(q) q 3 r U pode forçar uma vitória em no máximo r movimentos se e somente se Ur(q) Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

König estende o teorema de Zermelo Lema: Toda árvore infinitamente gerada possui um ramo infinito. => Se não há limite (número de passos) para uma posição vencedora então esta não é vencedora, pois em cada posição só há um número finito de movimentos para o adversário. Kalmár e a determinância de jogos assemelhados ao Xadrez Satz III: Em qualquer jogo J potencialmente infinito assemelhado ao Xadrez, se O jogador A não pode forçar a vitória então o jogador B garante pelo menos o empate Corolário: No Xadrez infinito ou as brancas tem uma estratégia vencedora, ou as pretas tem uma estratégia vencedora ou ambas podem garantir o empate. O jogo tem valor, é determinado. Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Nash 1950, Kuhn 1953 Teorema: Todo jogo finito com informação perfeita, de n jogadores, tem um ponto de equilíbrio. Prova: Por indução todo jogo com menos que m nós possui um ponto de equilíbrio Se r é um nó chance, então combine todos pontos de equilíbrio dos subjogos i; Senão o ponto de equilíbrio para r é maximizar os pontos de equilíbrio de cada um dos jogadores com relação ao subjogos i r m nós 1 Jan/2004 i k Prog. Din. , Min. Max Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Equação da onda u ut(x, 0) = g(x) e u(x, t) = F(x+ct)+G(x-ct) u(x, 0) = f(x) D’Alembert 1747 + Euler 1748 Daniel Bernouli 1753 xt u(x, t) = 2 0 (sinn ysinn xcosn ct)f(y)dy + 2 0 (1/n) (sinn ysinn xsinn ct)g(y)dy Lagrange 1759 Prof. Edward Hermann Haeusler TECMF-DI-PUC-Rio Teoria da Computação: e Fund. Matemática 48

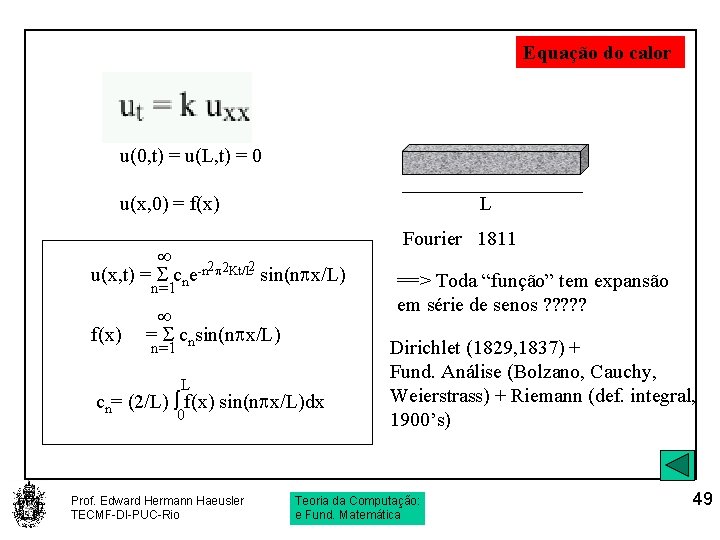
Equação do calor u(0, t) = u(L, t) = 0 u(x, 0) = f(x) L u(x, t) = cne-n 2 2 Kt/L 2 sin(n x/L) n=1 f(x) = cnsin(n x/L) n=1 L cn= (2/L) f(x) sin(n x/L)dx 0 Prof. Edward Hermann Haeusler TECMF-DI-PUC-Rio Fourier 1811 ==> Toda “função” tem expansão em série de senos ? ? ? Dirichlet (1829, 1837) + Fund. Análise (Bolzano, Cauchy, Weierstrass) + Riemann (def. integral, 1900’s) Teoria da Computação: e Fund. Matemática 49

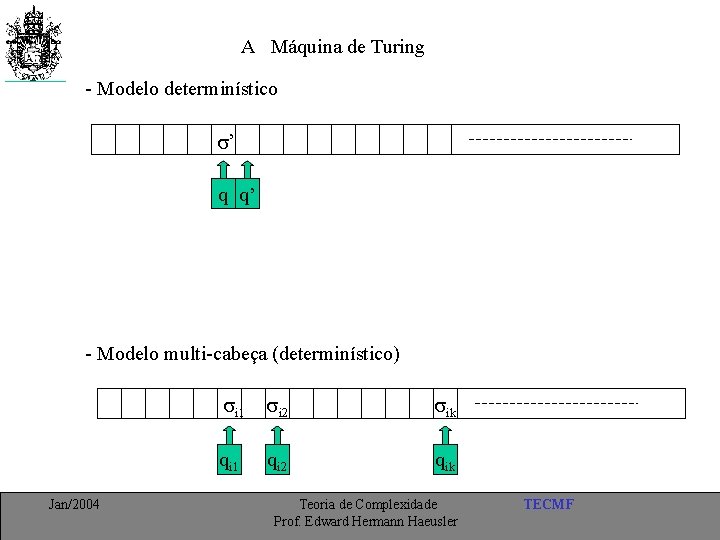
A Máquina de Turing - Modelo determinístico ’ q q’ - Modelo multi-cabeça (determinístico) Jan/2004 i 1 i 2 ik qi 1 qi 2 qik Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

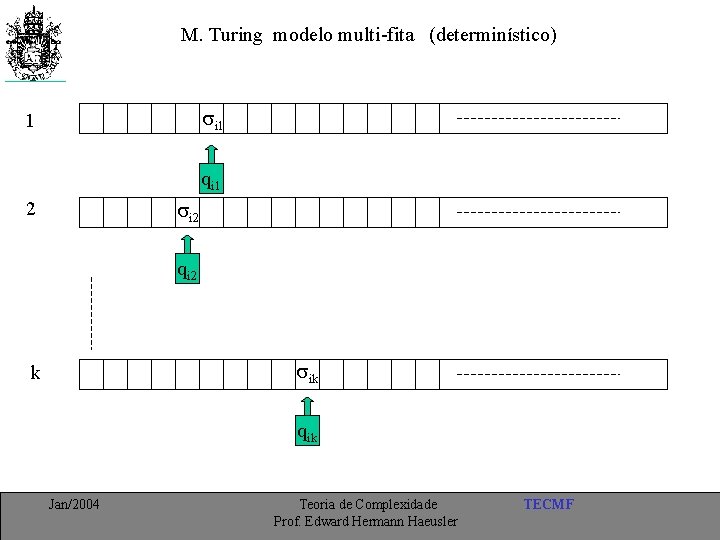
M. Turing modelo multi-fita (determinístico) i 1 1 qi 1 i 2 2 qi 2 ik k qik Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

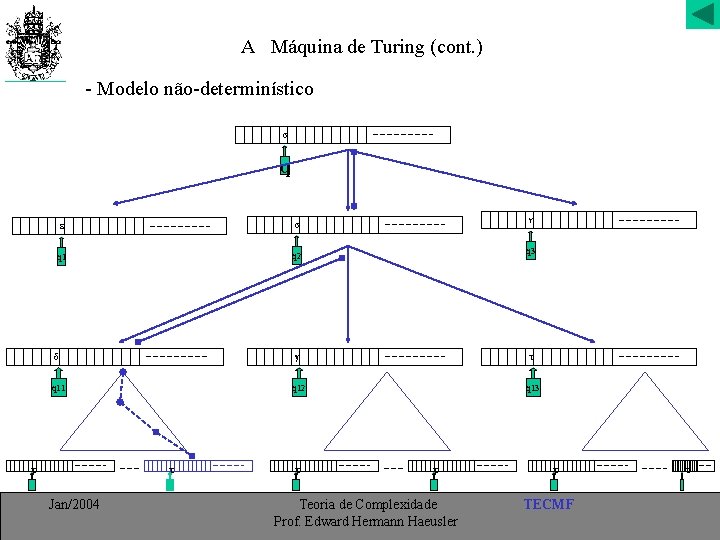
A Máquina de Turing (cont. ) - Modelo não-determinístico q q 1 q 2 q 3 q 11 q 12 q 13 Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF

QSAT é PSPACE-completo x( q x) expressa q p p pode ser expresso como x(x) QSAT está em PSPACE Para qualquer MTD M que decide um problema usando espaço p(|w|) -Codifica-se os estados globais de M em strings de p(w) bits EGM(x 1, x 2, . . . , x. P(n)) descreve um estado global Descubra como diminiur o tamanho de Codifica-se a execução de um passo da computação de M para não sercomo Exponencial Passo (x, y) , onde EG (x) e EG (y) M M M Codifica-se estado global final (aceitação) Final. M(x) Predicado para computação global. Evolui. M(x, y) = Passo. M(x, y) z(Evolui. M(x, z) Evolui. M(z, y)) Fórmula associada a aceitação de w por M Aceita. M(w) = EGM(w) z(Evolui. M(w, z) Final. M(z)) Jan/2004 Teoria de Complexidade Prof. Edward Hermann Haeusler TECMF