Teoria Microeconmica II Introduo Teoria dos Jogos Prof


























- Slides: 30

Teoria Microeconômica II: Introdução à Teoria dos Jogos Prof. João Manoel Pinho de Mello jmpm@econ. puc-rio. br Agosto, 2006

Revisão Principais conceitos e definições

Revisão n n Jogo estático n “Common knowledge” n Eliminação de estratégias estritamente dominadas n Equilíbrio de Nash n Estratégias mistas Jogo Dinâmico n Estratégia n Subjogo n Equilíbrio de Nash Perfeito em Subjogos

HOJE: Jogos Repetidos Horizonte finito e infinito Reputação e credibilidade Punições

Dilema dos Prisioneiros n Considere a seguinte versão do dilema dos prisioneiros. 2 1 n C NC C 1, 1 5, 0 NC 0, 5 4, 4 Pergunta: há meios de implementar cooperação em relações duradouras?

Horizonte Finito

Dilema dos prisioneiros em 2 períodos n Taxa de desconto: = 1 n Expansão da árvore é exponencial: n n n 1 o período: 4 resultados possíveis 2 o período: 16 resultados possíveis Estratégia: deve estabelecer o que será feito por cada jogador, em cada história possível do jogo.

Indução retroativa n Menor subjogo: é o próprio jogo constituinte; independente da história pregressa. n EN do menor subjogo: (C, C).

1 o período n Considerando que no segundo período será jogado (C, C), o primeiro período é representado por: 2 1 C NC C 2, 2 6, 1 NC 1, 6 5, 5

Equilíbrio de Nash Perfeito em Subjogos n Jogador i =1, 2: (C; C, C, C, C) n O ENPS é único. n Não há como implementar cooperação. n Caso houvesse N períodos, o resultado seria análogo.

Proposição Caso o jogo constituinte tenha um único equilíbrio de Nash, o jogo repetido N vezes também terá um único equilíbrio de Nash perfeito em subjogos. Esse ENPS corresponde à repetição dos equilíbrios do jogo constituinte.

Cooperação em jogos com horizonte finito n Suponha que, por alguma razão, haja uma nova possibilidade no jogo constituinte, representada por X. 2 1 C NC X C 1, 1 5, 0 0, 0 NC 0, 5 4, 4 0, 0 X 0, 0 3, 3

Sustentando cooperação n Considere o seguinte par de estratégias (s 1, s 2) : n n n Primeiro período: NC Segundo período: X caso tenha ocorrido (NC, NC); C caso contrário. Objetivo: ao invés de caracterizar o conjunto de todos os equilíbrios, iremos mostrar que as estratégias acima constituem um ENPS.

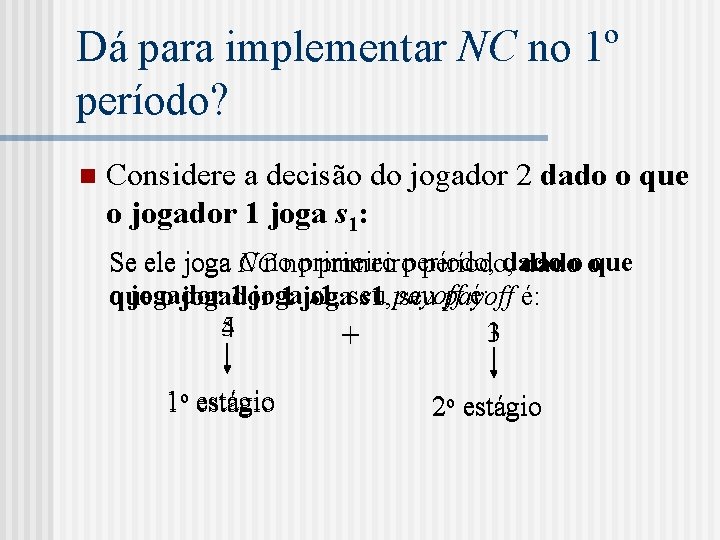
Dá para implementar NC no 1º período? n Considere a decisão do jogador 2 dado o que o jogador 1 joga s 1: Se ele joga C NCnonoprimeiroperíodo, dadoo oque jogador 1 joga s 1, seu é: é: o jogador 1 joga s 1, payoff seu payoff 54 13 + 1 o estágio 2 o estágio

Características n Só é possível implementar cooperação em jogos repetidos com horizonte finito se o jogo constituinte apresentar equilíbrios múltiplos. apenas as ameaças críveis de punições futuras podem afetar o comportamento corrente. n Caso haja um único EN no jogo constituinte, será jogado em cada repetição.

Horizonte Infinito

Estrutura n Jogo constituinte é o mesmo que antes n Infinitas repetições – se aplica para relações duradouras que não possuem prazo de validade. n Taxa de desconto: 0 < < 1. n n Impaciência. Probabilidade do jogo se repetir por mais 1 período.

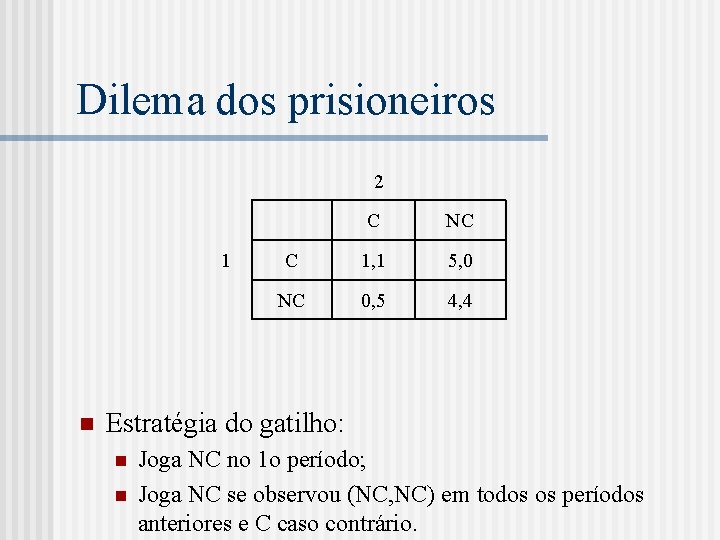
Dilema dos prisioneiros 2 1 n C NC C 1, 1 5, 0 NC 0, 5 4, 4 Estratégia do gatilho: n n Joga NC no 1 o período; Joga NC se observou (NC, NC) em todos os períodos anteriores e C caso contrário.

Teste n A estratégia do gatilho constitui um equilíbrio de Nash perfeito em subjogos? n 2 tipos relevantes de subjogos: n n n subjogos de “cooperação”; subjogos de “não-cooperação”. Naqueles subjogos de não-cooperação, a estratégia prevê um equilíbrio de Nash do jogo constituinte.

Subjogos de cooperação n Nos subjogos de cooperação, as estratégias constituem equilíbrio se: 4+4 +4 2+. . . ≥ 5+ + 2. . . 4/(1 - ) ≥ 5+ /(1 - ) ≥ 1/4.

Implementando o que é possível n O que acontece se <1/4 ? n n C não é implementável Considere uma versão modificada do dilema dos prisioneiros, em que: 2 1 C NC C 1, 1 5, 0 NC 0, 5 M, M

Continuação n Estratégia do gatilho: n n n Joga NC no 1 o período; Joga NC se observou (NC, NC) em todos os períodos anteriores e C caso contrário. Nos subjogos de cooperação, as estratégias constituem equilíbrio se: M+M +M 2+. . . ≥ 5+ + 2. . . M/(1 - ) ≥ 5+ /(1 - ) M ≥ 5 -4.

Lição Como os jogadores descontam muito o futuro, tornase necessária uma compensação maior para que a cooperação ocorra.

Implementando cooperação com punições mais brandas n A estratégia do gatilho envolve punições muito agressivas que, diante de um desvio, penaliza os jogadores indefinidamente. n Considere o seguinte par de estratégias (“stick and carrot”): n n n Joga NC no 1 o período; Joga NC se observou (NC, NC) ou (C, C) no período anterior; Joga C caso contrário.

Estratégia n t ação de 1 ação de 2 k NC NC k+1 NC C k+2 C C k+3 NC NC Diante de um desvio em k+1, a punição tem duração de apenas 1 período.

Equilíbrio de Nash Perfeito em Subjogos n Nos subjogos de punição, a análise é a mesma da estratégia do gatilho. n Nos subjogos de cooperação, as estratégias constituem equilíbrio se: 4+4 +4 2+. . . ≥ 5+ +4 2. . . 4+4 ≥ 5+ ≥ 1/3.

Lição n Punições mais brandas requerem uma taxa de desconto mínima maior para a implementação da cooperação.

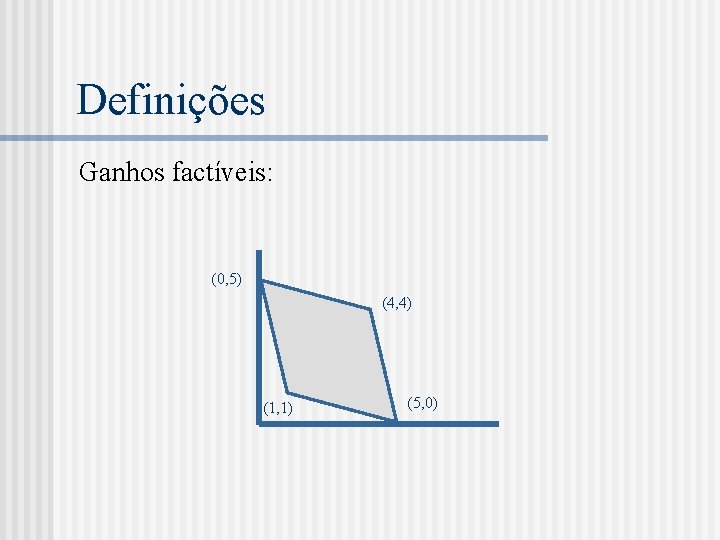
Definições Ganhos factíveis: (0, 5) (4, 4) (1, 1) (5, 0)

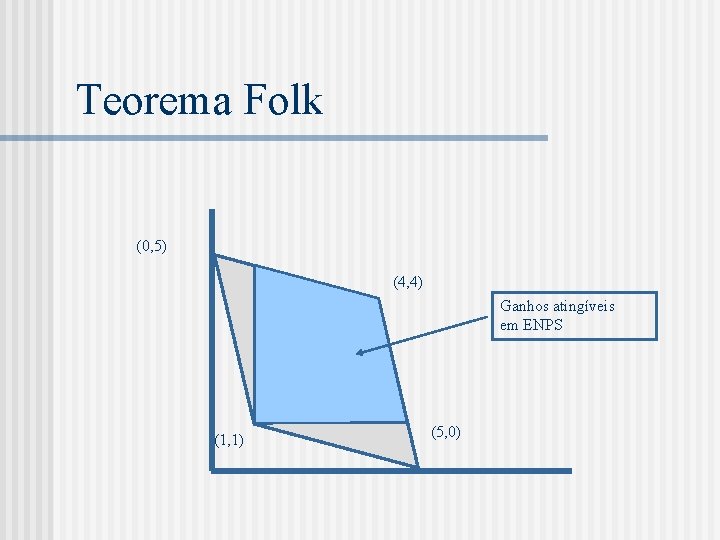
Teorema Folk n Friedman, 1971 Seja G um jogo estratégico com informação completa e (e 1, . . . , e. N) os ganhos de um equilíbrio de Nash de G. Seja (x 1, . . . , x. N) um vetor de ganhos factíveis de G. Se xi > ei para todo i e for suficientemente próximo de 1, existe um ENPS do jogo repetido com horizonte infinito que atinge (x 1, . . . , x. N) como ganho médio.

Teorema Folk (0, 5) (4, 4) Ganhos atingíveis em ENPS (1, 1) (5, 0)
 Os jogos eletrônicos substituirão os jogos populares
Os jogos eletrônicos substituirão os jogos populares Teoria dos jogos
Teoria dos jogos O dilema do prisioneiro
O dilema do prisioneiro Jogos populares do brasil e do mundo
Jogos populares do brasil e do mundo Jogos feitos em lua
Jogos feitos em lua Saltar ao elástico portugal
Saltar ao elástico portugal Instituto de supervisão de jogos
Instituto de supervisão de jogos O que são jogos cooperativos
O que são jogos cooperativos Jogos online
Jogos online Solidariedade e cooperação nos jogos esportivos
Solidariedade e cooperação nos jogos esportivos O que são jogos pré-desportivos
O que são jogos pré-desportivos Sequestro gunbound
Sequestro gunbound Jogos online gratis
Jogos online gratis Jogos criativos para jovens
Jogos criativos para jovens Jogos cooperativos sem perdedores
Jogos cooperativos sem perdedores Chiqueirão
Chiqueirão Oficina de jogos e brincadeiras
Oficina de jogos e brincadeiras Jogos e brincadeiras
Jogos e brincadeiras O que são jogos pré-desportivos
O que são jogos pré-desportivos Quem foi ted lentz
Quem foi ted lentz Efuturo jogos educativos
Efuturo jogos educativos Dos moviles parten en el mismo sentido a 10m/s y 30m/s
Dos moviles parten en el mismo sentido a 10m/s y 30m/s Laberintos cuento
Laberintos cuento Direitos do cidadão
Direitos do cidadão El que habla dos idiomas vale por dos
El que habla dos idiomas vale por dos Donde habla la biblia de los dos caminos
Donde habla la biblia de los dos caminos Los envió de dos en dos
Los envió de dos en dos Poliedro convexo
Poliedro convexo Arestas vértices e faces
Arestas vértices e faces Teoria dos direitos fundamentais robert alexy
Teoria dos direitos fundamentais robert alexy Teoria dos jogo
Teoria dos jogo