Teoria Microeconmica II Introduo Teoria dos Jogos Prof

Teoria Microeconômica II: Introdução à Teoria dos Jogos Prof. João Manoel Pinho de Mello jmpm@econ. puc-rio. br Agosto, 2006

Revisão Principais conceitos e definições

Revisão n n Jogo estático n “Common knowledge” n Eliminação de estratégias estritamente dominadas n Equilíbrio de Nash n Estratégias mistas Jogo Dinâmico n Estratégia n Subjogo n Equilíbrio de Nash Perfeito em Subjogos

HOJE: Jogos Repetidos Horizonte finito e infinito Reputação e credibilidade Punições

Dilema dos Prisioneiros n Considere a seguinte versão do dilema dos prisioneiros. 2 1 n C NC C 1, 1 5, 0 NC 0, 5 4, 4 Pergunta: há meios de implementar cooperação em relações duradouras?

Horizonte Finito

Dilema dos prisioneiros em 2 períodos n Taxa de desconto: = 1 n Expansão da árvore é exponencial: n n n 1 o período: 4 resultados possíveis 2 o período: 16 resultados possíveis Estratégia: deve estabelecer o que será feito por cada jogador, em cada história possível do jogo.

Indução retroativa n Menor subjogo: é o próprio jogo constituinte; independente da história pregressa. n EN do menor subjogo: (C, C).

1 o período n Considerando que no segundo período será jogado (C, C), o primeiro período é representado por: 2 1 C NC C 2, 2 6, 1 NC 1, 6 5, 5

Equilíbrio de Nash Perfeito em Subjogos n Jogador i: (C; C, C, C, C) n O ENPS é único. n Não há como implementar cooperação. n Caso houvesse N períodos, o resultado seria análogo.

Proposição Caso o jogo constituinte tenha um único equilíbrio de Nash, o jogo repetido N vezes também terá um único equilíbrio de Nash perfeito em subjogos. Esse ENPS corresponde à repetição dos equilíbrios do jogo constituinte.

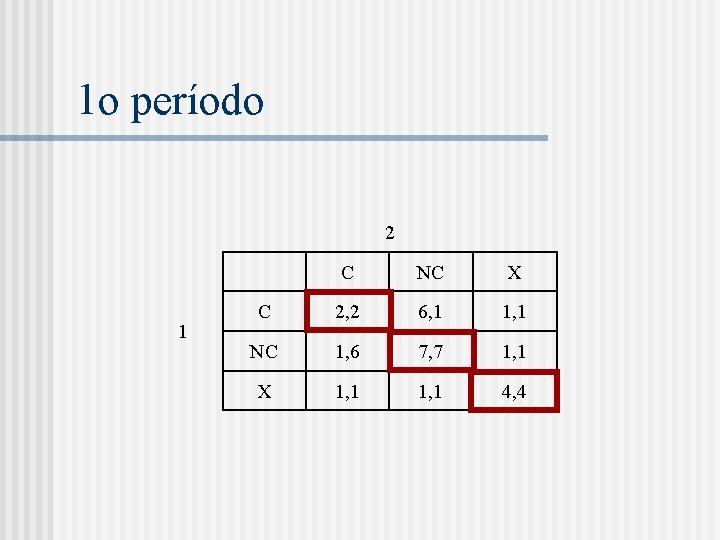
Cooperação em jogos com horizonte finito n Suponha que, por alguma razão, haja uma nova possibilidade no jogo constituinte, representada por X. 2 1 C NC X C 1, 1 5, 0 0, 0 NC 0, 5 4, 4 0, 0 X 0, 0 3, 3

Sustentando cooperação n Considere o seguinte par de estratégias: n n n Primeiro período: NC Segundo período: X caso tenha ocorrido (NC, NC); C caso contrário. Objetivo: ao invés de caracterizar o conjunto de todos os equilíbrios, iremos mostrar que as estratégias acima constituem um ENPS.

Indução retroativa n 2 o período: n As estratégias determinam que ambos escolham C ou ambos escolham X. n Como (C, C) e (X, X) são EN do jogo constituinte, não há problema.

1 o período 2 1 C NC X C 2, 2 6, 1 1, 1 NC 1, 6 7, 7 1, 1 X 1, 1 4, 4

Características n Só é possível implementar cooperação em jogos repetidos com horizonte finito se o jogo constituinte apresentar equilíbrios múltiplos. apenas as ameaças críveis de punições futuras podem afetar o comportamento corrente. n Caso haja um único EN no jogo constituinte, será jogado em cada repetição.

Horizonte Infinito

Estrutura n Jogo constituinte G. n Infinitas repetições – se aplica para relações duradouras que não possuem prazo de validade. n Taxa de desconto: 0< <1. n n Impaciência. Probabilidade do jogo se repetir por mais 1 período.

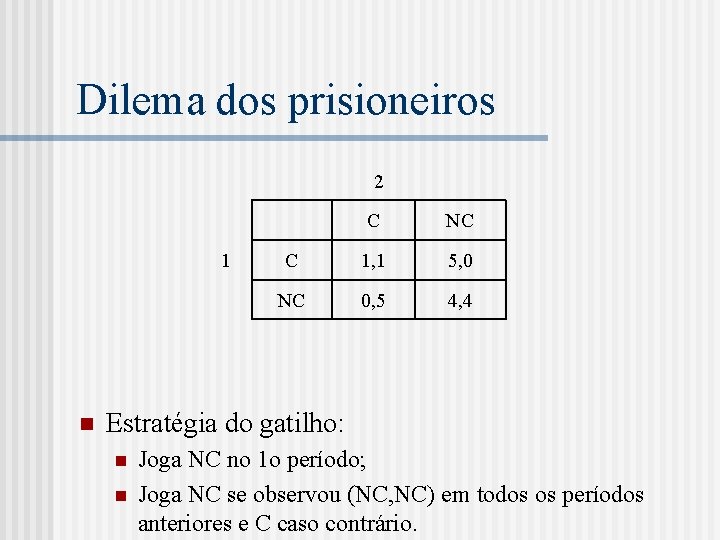
Dilema dos prisioneiros 2 1 n C NC C 1, 1 5, 0 NC 0, 5 4, 4 Estratégia do gatilho: n n Joga NC no 1 o período; Joga NC se observou (NC, NC) em todos os períodos anteriores e C caso contrário.

Teste n A estratégia do gatilho constitui um equilíbrio de Nash perfeito em subjogos? n 2 tipos relevantes de subjogos: n n n subjogos de “cooperação”; subjogos de “não-cooperação”. Naqueles subjogos de não-cooperação, a estratégia prevê um equilíbrio de Nash do jogo constituinte.

Subjogos de cooperação n Nos subjogos de cooperação, as estratégias constituem equilíbrio se: 4+4 +4 2+. . . ≥ 5+ + 2. . . 4/(1 - ) ≥ 5+ /(1 - ) ≥ 1/4.

Implementando o que é possível n O que acontece se <1/4 ? n Considere uma versão modificada do dilema dos prisioneiros, em que: 2 1 C NC C 1, 1 5, 0 NC 0, 5 M, M

Continuação n Estratégia do gatilho: n n n Joga NC no 1 o período; Joga NC se observou (NC, NC) em todos os períodos anteriores e C caso contrário. Nos subjogos de cooperação, as estratégias constituem equilíbrio se: M+M +M 2+. . . ≥ 5+ + 2. . . M/(1 - ) ≥ 5+ /(1 - ) M ≥ 5 -4.

Lições n Como os jogadores descontam muito o futuro, tornase necessária uma compensação maior para que a cooperação ocorra. n No jogo analisado, existem apenas duas estratégias. Não há possibilidade de implementar uma cooperação que envolva menos incentivos ao desvio.

Implementando cooperação com punições mais brandas n A estratégia do gatilho envolve punições muito agressivas que, diante de um desvio, penaliza os jogadores indefinidamente. n Considere o seguinte par de estratégias (“stick and carrot”): n n n Joga NC no 1 o período; Joga NC se observou (NC, NC) ou (C, C) no período anterior; Joga C caso contrário.

Estratégia n t ação de 1 ação de 2 k NC NC k+1 NC C k+2 C C k+3 NC NC Diante de um desvio em k+1, a punição tem duração de apenas 1 período.

Equilíbrio de Nash Perfeito em Subjogos n Nos subjogos de punição, a análise é a mesma da estratégia do gatilho. n Nos subjogos de cooperação, as estratégias constituem equilíbrio se: 4+4 +4 2+. . . ≥ 5+ +4 2. . . 4+4 ≥ 5+ ≥ 1/3.

Lição n Punições mais brandas requerem uma taxa de desconto mínima maior para a implementação da cooperação.

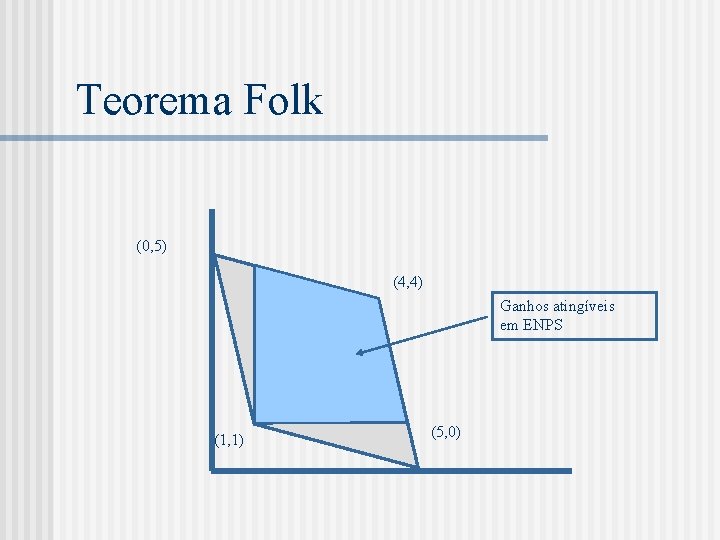
Definições n Ganho médio: 1, 2, 3, . . . (1 - ) t t-1 t. n Ganhos factíveis: (0, 5) (4, 4) (1, 1) (5, 0)

Teorema Folk n Friedman, 1971 Seja G um jogo estratégico com informação completa e (e 1, . . . , e. N) os ganhos de um equilíbrio de Nash de G. Seja (x 1, . . . , x. N) um vetor de ganhos factíveis de G. Se xi > ei para todo i e for suficientemente próximo de 1, existe um ENPS do jogo repetido com horizonte infinito que atinge (x 1, . . . , x. N) como ganho médio.

Teorema Folk (0, 5) (4, 4) Ganhos atingíveis em ENPS (1, 1) (5, 0)