O Homem imaginou as formas que se encontram

O Homem imaginou as formas que se encontram na Natureza de uma forma ainda mais perfeita e deu-lhes o nome de SÓLIDOS GEOMÉTRICOS.

Sólido geométrico – porção finita de espaço limitada por superfícies planas e curvas. É um objecto tridimensional, isto é, tem largura, comprimento e altura.

Os sólidos geométricos dividem-se em dois grandes grupos:

POLIEDROS

NÃO POLIEDROS

Poliedros sólidos geométricos limitados apenas por superfícies planas. Não Poliedros sólidos geométricos que são limitados, pelo menos, por uma superfície curva.

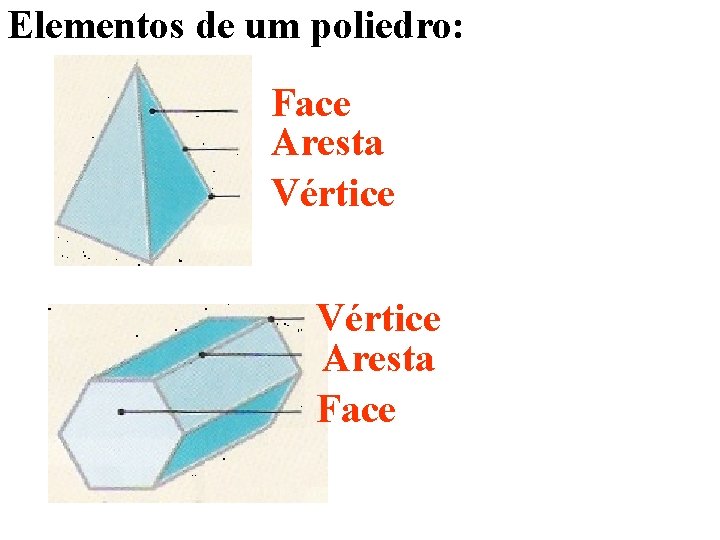
Elementos de um poliedro: Ø Faces – Qualquer das superfícies de um sólido. Ø Arestas – Linha que resulta do encontro de duas faces do poliedro. Ø Vértice – Cada um dos pontos de um polígono.

Elementos de um poliedro: Face Aresta Vértice Aresta Face

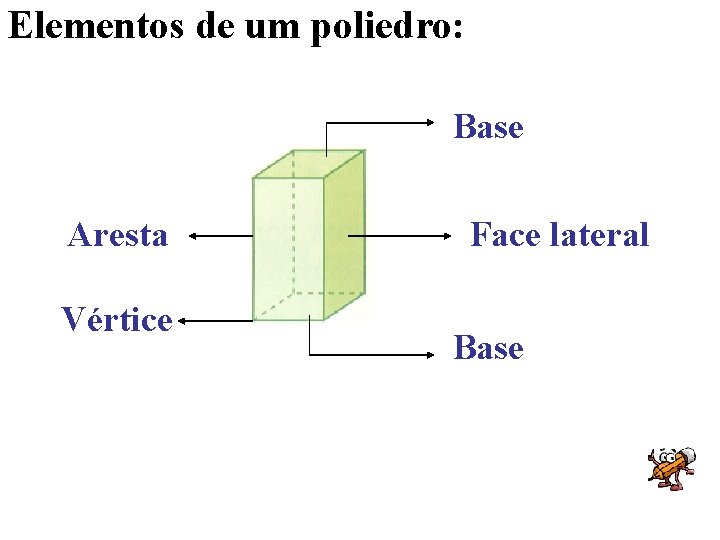
Elementos de um poliedro: Base Aresta Vértice Face lateral Base

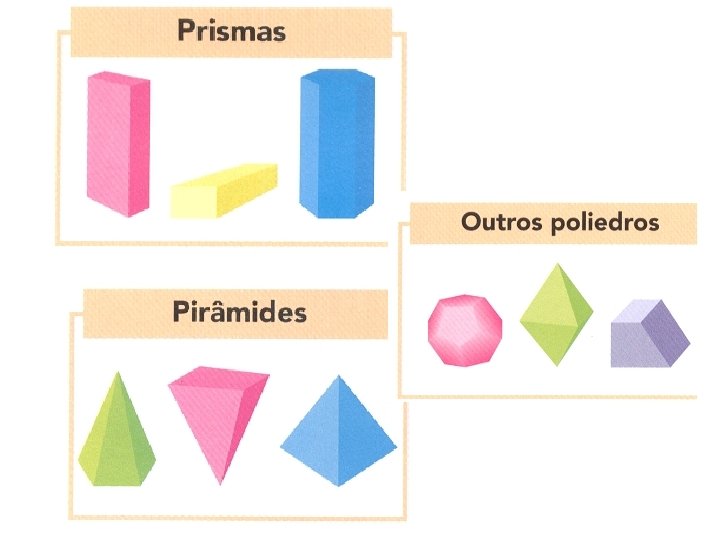
Os poliedros podem agrupar-se em:

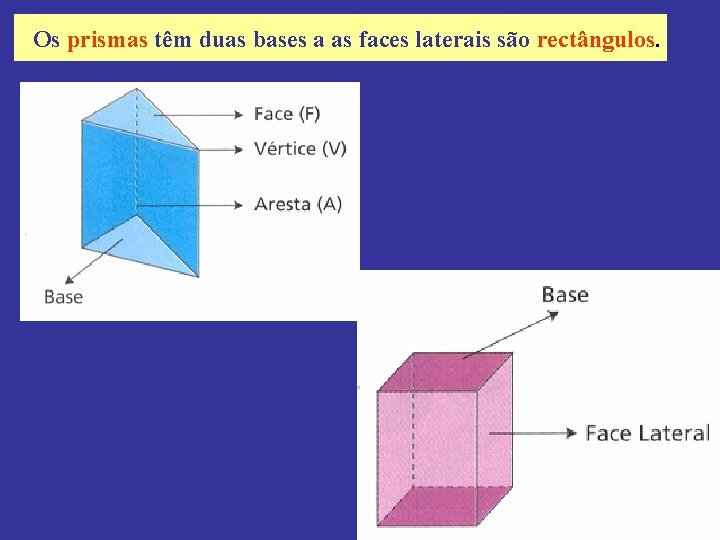
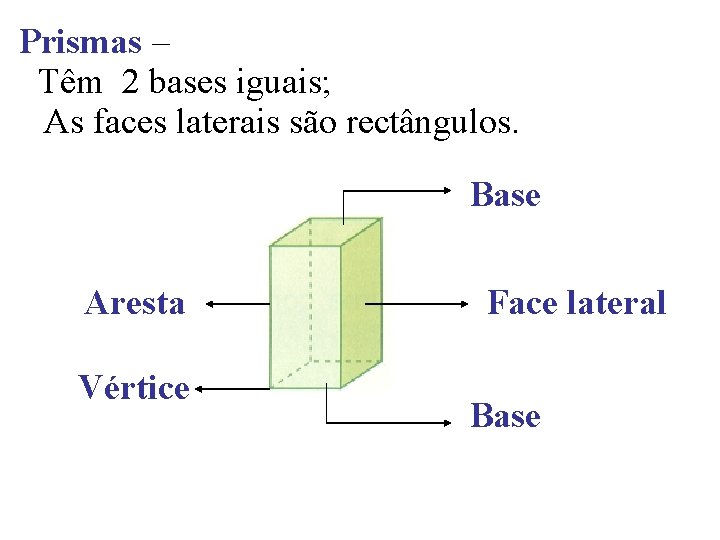
Os prismas têm duas bases a as faces laterais são rectângulos.

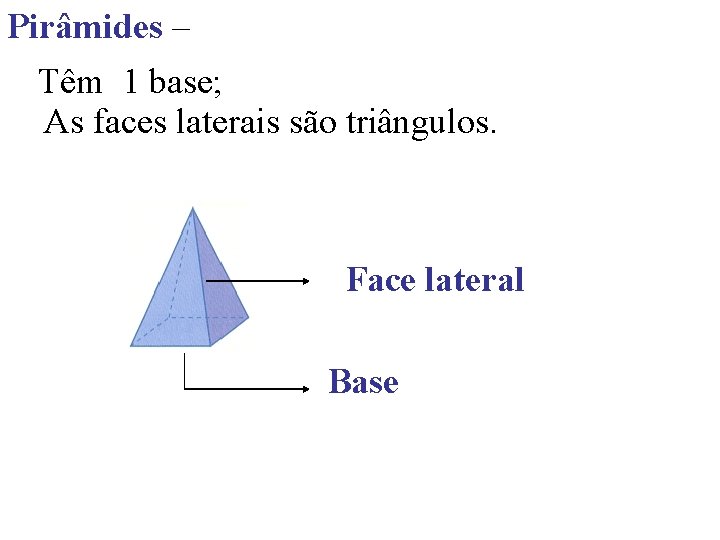
As pirâmides têm uma base e as faces laterais são triângulos.

Prismas – Têm 2 bases iguais; As faces laterais são rectângulos. Base Aresta Vértice Face lateral Base

Pirâmides – Têm 1 base; As faces laterais são triângulos. Face lateral Base

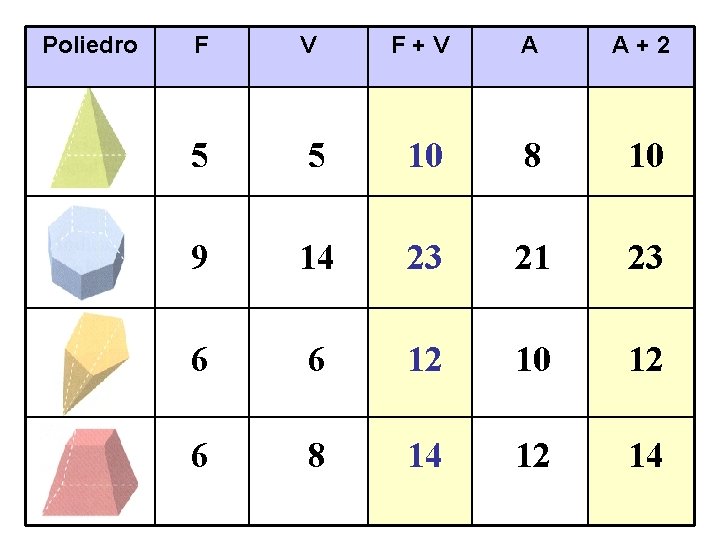
Poliedro F V F+V A A+2 5 5 10 8 10 9 14 23 21 23 6 6 12 10 12 6 8 14 12 14

Igualdade de Euler Num poliedro: F+V=A+2

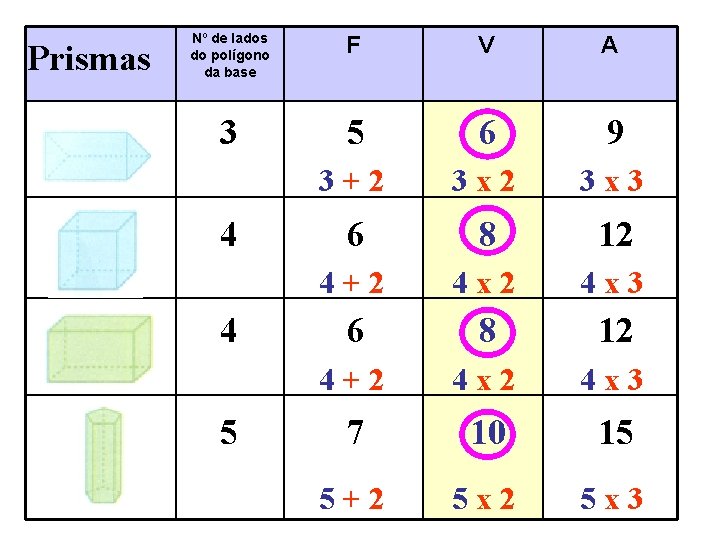
Prismas Nº de lados do polígono da base F V A 3 5 6 9 3+2 3 x 3 6 8 12 4+2 4 x 3 7 10 15 5+2 5 x 3 4 4 5

Num prisma: Ø O nº de faces é igual ao número de lados do polígono da base mais dois; Ø O nº de arestas é o triplo do número de lados do polígono da base; Ø O nº de vértices é um nº par e é o dobro do número de lados do polígono da base.

Observa o sólido: Quantas faces tem? Quantos vértices tem? Quantas arestas tem? 6 (4 + 2) 8 12 (4 x 2) (4 x 3) F+V=A+2 6 + 8 = 12 + 2 14 = 14

Observa o sólido: Quantas faces tem? Quantos vértices tem? Quantas arestas tem? 7 (5 + 2) 10 15 (5 x 2) (5 x 3)

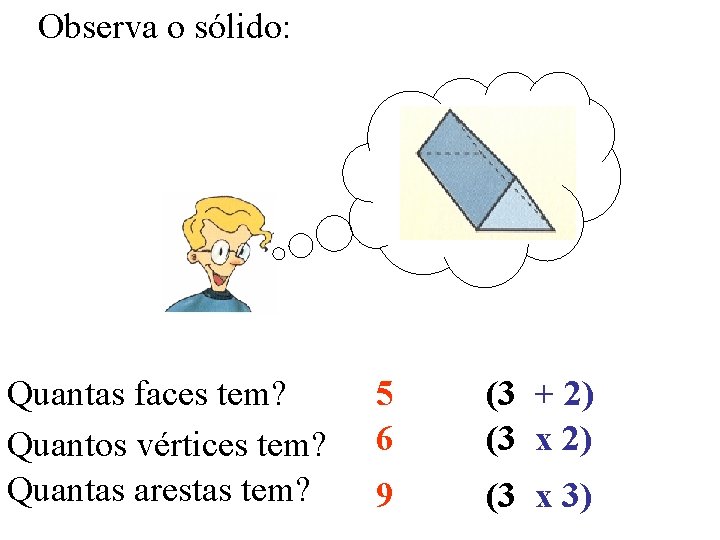
Observa o sólido: Quantas faces tem? Quantos vértices tem? Quantas arestas tem? 5 6 (3 + 2) (3 x 2) 9 (3 x 3)

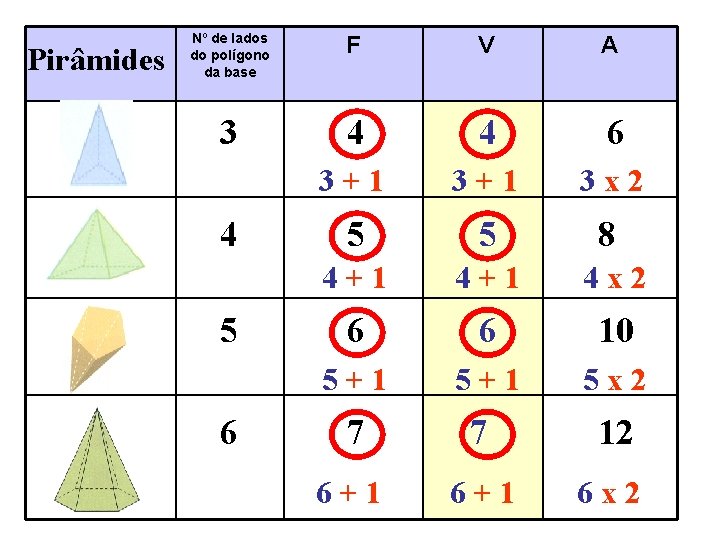
Pirâmides Nº de lados do polígono da base F V A 3 4 4 6 3+1 3 x 2 5 5 8 4+1 4 x 2 6 6 10 5+1 5 x 2 7 7 12 6+1 6 x 2 4 5 6

Numa pirâmide: Ø O nº de faces é igual ao número de lados do polígono da base mais um; Ø O nº de arestas é um nº par e é o dobro do número de lados do polígono da base; Ø O nº de vértices é igual ao número de lados do polígono da base mais um.

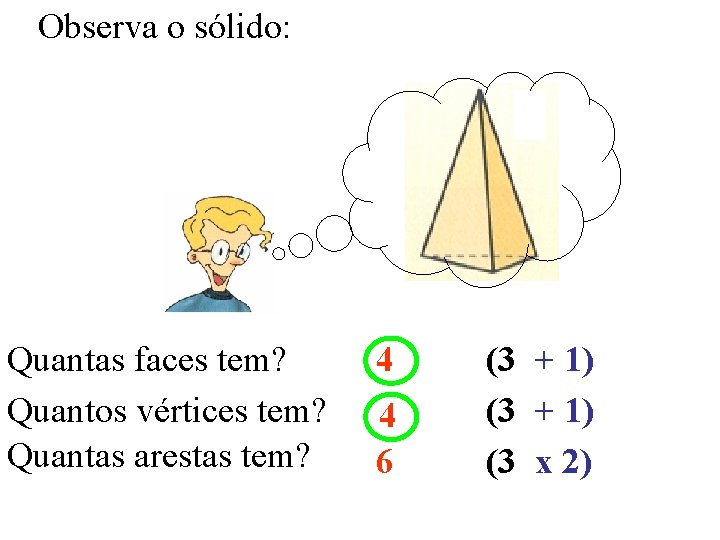
Observa o sólido: Quantas faces tem? Quantos vértices tem? Quantas arestas tem? 4 4 6 (3 + 1) (3 x 2)

Qual é o menor número de vértices que uma pirâmide pode ter? 4