Determinantes 1 Introduo A teoria dos determinantes teve








- Slides: 11

Determinantes 1. Introdução: A teoria dos determinantes teve origem em meados do século XVII, quando eram estudados processos para resolução de sistemas lineares de equações. 2. Definição: A toda matriz quadrada associa-se um número, denominado determinante da matriz, que é obtido por meio de operações entre os elementos da matriz. 3. Cálculo dos Determinantes: 3. 1. Determinantes da matriz de 1ª ordem O determinante da matriz quadrada de 1ª ordem é igual ao próprio elemento da matriz. Ex. : Prof. Elionardo Rochelly

3. 2. Determinantes da matriz de 2ª ordem O determinante da matriz quadrada de 2ª ordem é igual diferença entre os produtos dos elementos da diagonal principal e da diagonal secundária. Ex. : (Regra de Sarrus) 3. 3. Determinantes da matriz de 3ª ordem 1. Ao lado direito da matriz copiam-se as duas primeiras colunas. 2. Multiplicam-se os elementos da diagonal principal e, na mesma direção da diagonal principal, multiplicam-se os elementos das outras duas filas à sua direita. 3. Multiplicam-se os elementos da diagonal secundária e, na mesma direção, os elementos das outras duas filas à sua direita. 4. O determinante da matriz é a subtração dos produtos obtidos em 2 e 3. Ex. : 10 – 8 + 0 + 6 – 12 + 0 - - - + + + Prof. Elionardo Rochelly = -4

Propriedades dos Determinantes P 1. Fila Nula Se todos os elementos de uma fila de uma matriz A forem nulos, então det A = 0. 0 Ex. : P 2. Filas Paralelas Iguais ou Proporcionais Se duas filas paralelas de uma matriz A forem iguais ou proporcionais, então Ex. : e 2ª linha = 2 x 1ª linha Prof. Elionardo Rochelly det A = 0.

P 3. Matriz Transposta O determinante de uma matriz é igual ao de sua transposta. Ex. : = 16 + 0 – 20 + 3 + 0 = -1 = 16 – 20 + 3 + 0 = -1 P 4. Teorema de Binet Se A e B são matrizes quadradas de mesma ordem n, então: det(A. B) = det A. det B Ex. : det A = 10, det B = 6 e det A. det B = 6. 10 = 60 det A. det B = 13. 6 – 2. 9 = 78 – 18 = 60 Prof. Elionardo Rochelly

P 5. Matriz Triangular O determinante de uma matriz triangular é igual ao produto dos elementos da diagonal principal. Ex. : = 5. 1. 8 = 40 P 6. Troca de Filas Paralelas Se trocarmos de posição duas filas paralelas de uma matriz M, obteremos uma outra matriz M´, tal que: det M´ = - det M Ex. : Prof. Elionardo Rochelly

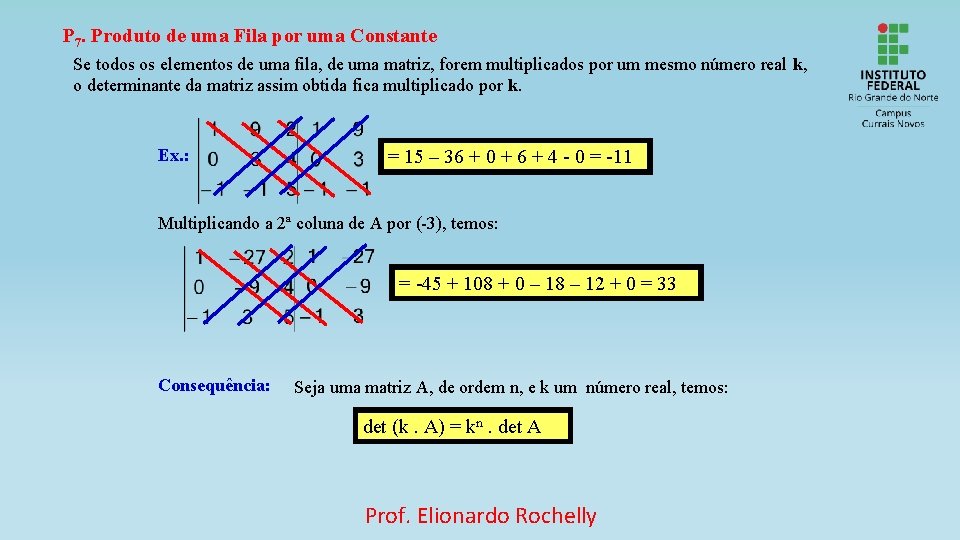
P 7. Produto de uma Fila por uma Constante Se todos os elementos de uma fila, de uma matriz, forem multiplicados por um mesmo número real k, o determinante da matriz assim obtida fica multiplicado por k. Ex. : = 15 – 36 + 0 + 6 + 4 - 0 = -11 Multiplicando a 2ª coluna de A por (-3), temos: = -45 + 108 + 0 – 18 – 12 + 0 = 33 Consequência: Seja uma matriz A, de ordem n, e k um número real, temos: det (k. A) = kn. det A Prof. Elionardo Rochelly

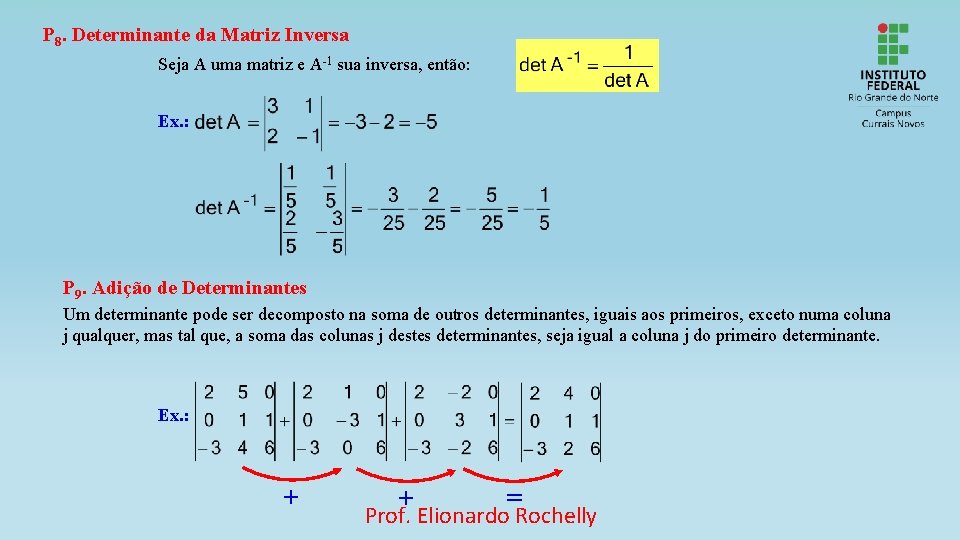
P 8. Determinante da Matriz Inversa Seja A uma matriz e A-1 sua inversa, então: Ex. : P 9. Adição de Determinantes Um determinante pode ser decomposto na soma de outros determinantes, iguais aos primeiros, exceto numa coluna j qualquer, mas tal que, a soma das colunas j destes determinantes, seja igual a coluna j do primeiro determinante. Ex. : + + = Prof. Elionardo Rochelly

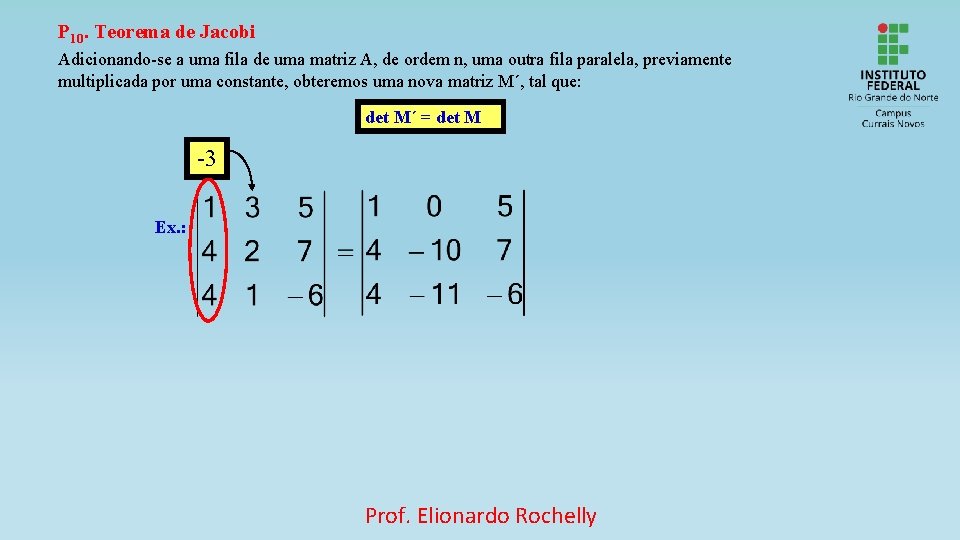
P 10. Teorema de Jacobi Adicionando-se a uma fila de uma matriz A, de ordem n, uma outra fila paralela, previamente multiplicada por uma constante, obteremos uma nova matriz M´, tal que: det M´ = det M -3 Ex. : Prof. Elionardo Rochelly

Matriz de Vandermonde Chamamos matriz de Vandermonde, ou das potências, toda matriz de ordem n 2, em que suas colunas são potências de mesma base, com expoente inteiro, variando de 0 à n – 1 (os elementos de cada coluna formam uma progressão geométrica de primeiro termo igual a 1). Obs. : Os elementos da 2ª linha são chamados elementos característicos da matriz. O determinante da matriz de Vandermonde é igual ao produto de todas as diferenças possíveis entre os elementos característicos e seus antecessores. Ex. : (3 – 2)(5 – 3)(7 – 2)(7 – 3)(7 – 5) 1. 3. 2. 5. 4. 2 240 Prof. Elionardo Rochelly

• Exemplos • Calcule o determinante a seguir: Prof. Elionardo Rochelly

a) 18 b) 12 c) 6 d) 0 Prof. Elionardo Rochelly