TRANSFORMACIONES ISOMTRICAS QU SON LAS TRANSFORMACIONES ISOMTRICAS Son










- Slides: 28

TRANSFORMACIONES ISOMÉTRICAS

¿QUÉ SON LAS TRANSFORMACIONES ISOMÉTRICAS? Son aquellos movimientos de una figura que no modifican las medidas ni la forma del objeto sobre el cual actúan; solo cambian la posición y el sentido. Actividad: Identificar cuales pares de imágenes son transformaciones Isométricas.

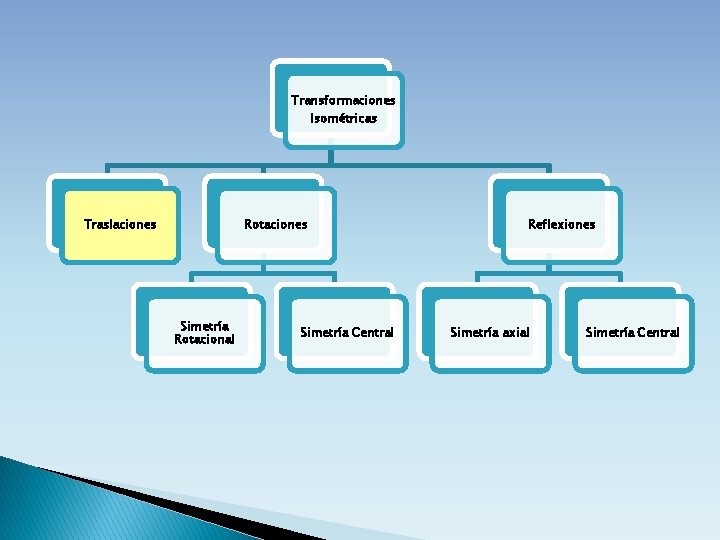
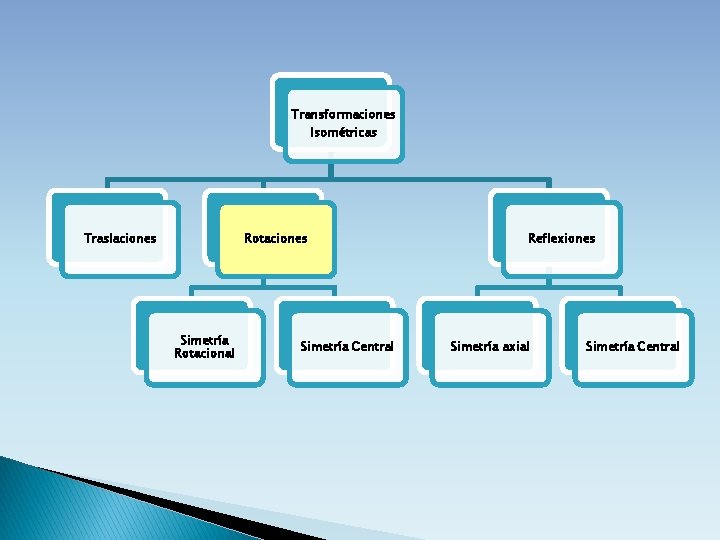
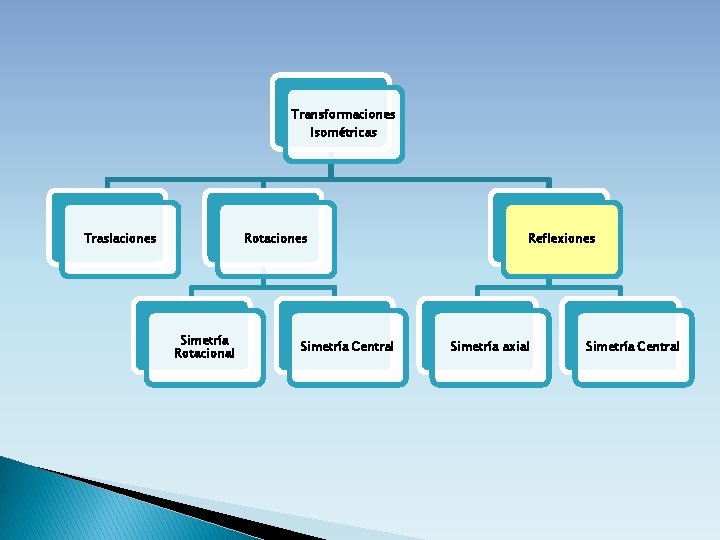
Transformaciones Isométricas Traslaciones Rotaciones Simetría Rotacional Simetría Central Reflexiones Simetría axial Simetría Central

VECTOR Se representa gráficamente por una flecha o un segmento de recta dirigido: u Un vector indica: v Dirección: Horizontal, vertical u oblicua. v Sentido: Derecha, izquierda, arriba, abajo. v Distancia o Magnitud : Es la distancia que existe entre el punto inicial y la posición final de cualquier punto de la figura que se desplaza.

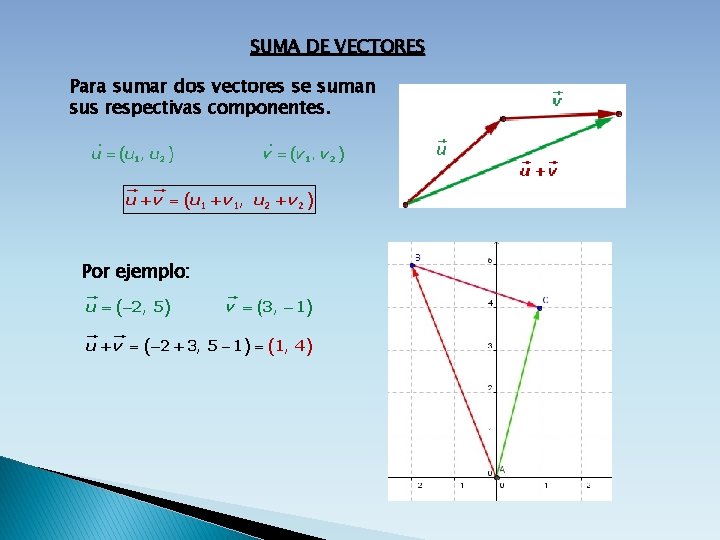
SUMA DE VECTORES Para sumar dos vectores se suman sus respectivas componentes. Por ejemplo:

MULTIPLICACIÓN DE UN VECTOR POR UN ESCALAR El producto de un número k por un vector es otro vector: üDe igual dirección que el vector. üDel mismo sentido que el vector, si k es positivo. üDe sentido contrario del vector, si k es negativo. Las componentes del vector resultante se obtienen multiplicando por K las coordenadas del vector. Por ejemplo:

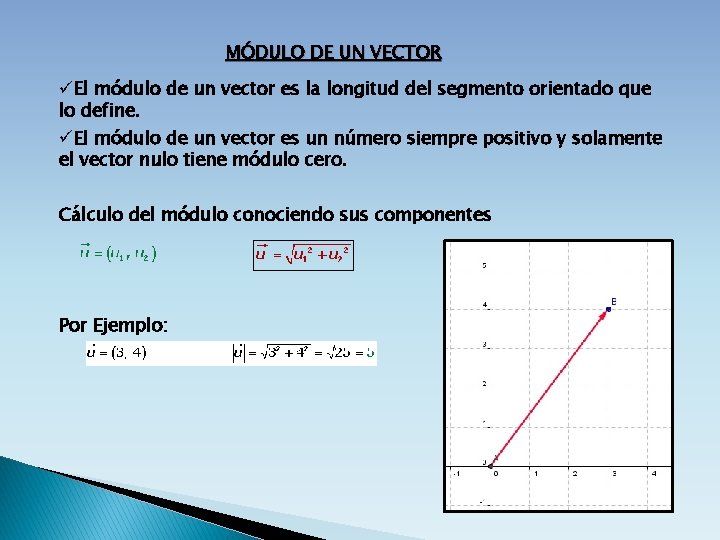
MÓDULO DE UN VECTOR üEl módulo de un vector es la longitud del segmento orientado que lo define. üEl módulo de un vector es un número siempre positivo y solamente el vector nulo tiene módulo cero. Cálculo del módulo conociendo sus componentes Por Ejemplo:

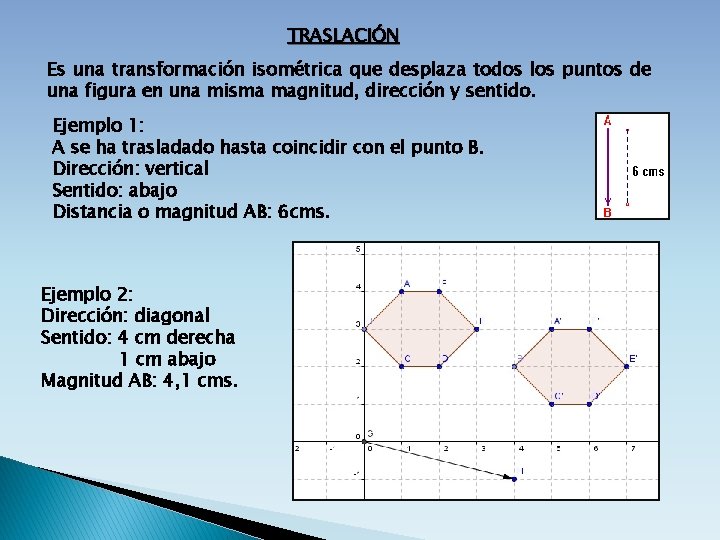
TRASLACIÓN Es una transformación isométrica que desplaza todos los puntos de una figura en una misma magnitud, dirección y sentido. Ejemplo 1: A se ha trasladado hasta coincidir con el punto B. Dirección: vertical Sentido: abajo Distancia o magnitud AB: 6 cms. Ejemplo 2: Dirección: diagonal Sentido: 4 cm derecha 1 cm abajo Magnitud AB: 4, 1 cms.

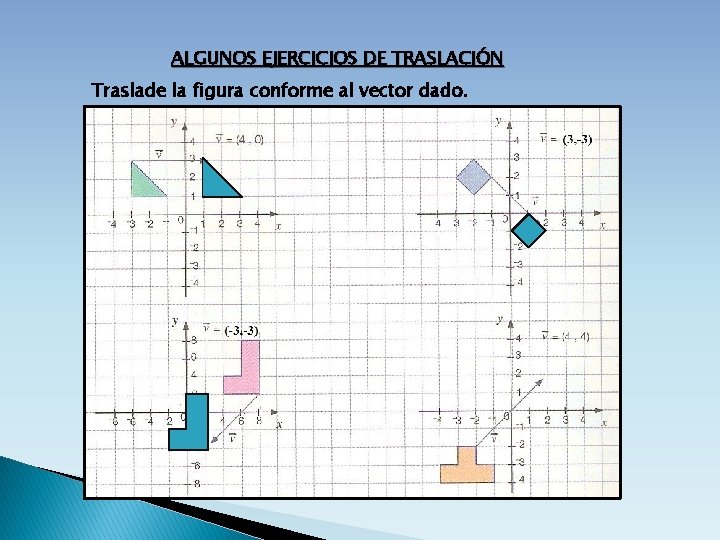
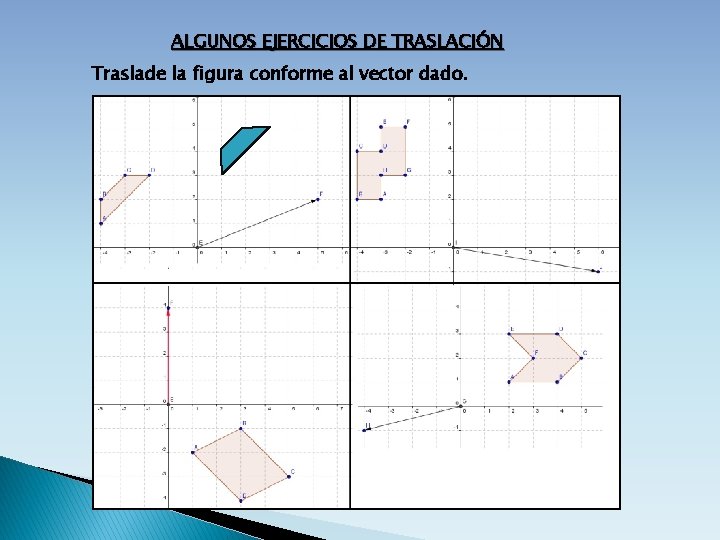
ALGUNOS EJERCICIOS DE TRASLACIÓN Traslade la figura conforme al vector dado.

ALGUNOS EJERCICIOS DE TRASLACIÓN Traslade la figura conforme al vector dado.

RESUMEN CLASE ANTERIOR Verifiquemos lo aprendido, indicando una definición para uno de los siguientes conceptos. v Transformación Isométrica v Tipos de transformaciones Isométricas v Vector v Suma de vectores v Multiplicación de un vector por un escalar v Módulo de un vector v Traslación

Transformaciones Isométricas Traslaciones Rotaciones Simetría Rotacional Simetría Central Reflexiones Simetría axial Simetría Central

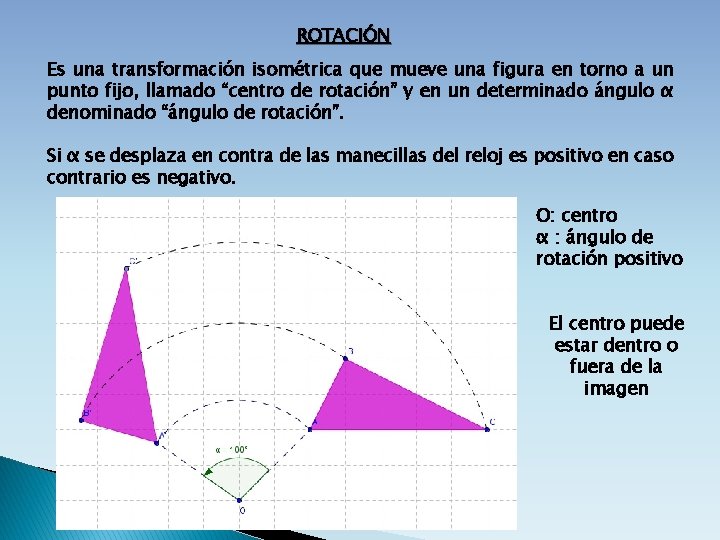
ROTACIÓN Es una transformación isométrica que mueve una figura en torno a un punto fijo, llamado “centro de rotación” y en un determinado ángulo α denominado “ángulo de rotación”. Si α se desplaza en contra de las manecillas del reloj es positivo en caso contrario es negativo. O: centro α : ángulo de rotación positivo El centro puede estar dentro o fuera de la imagen

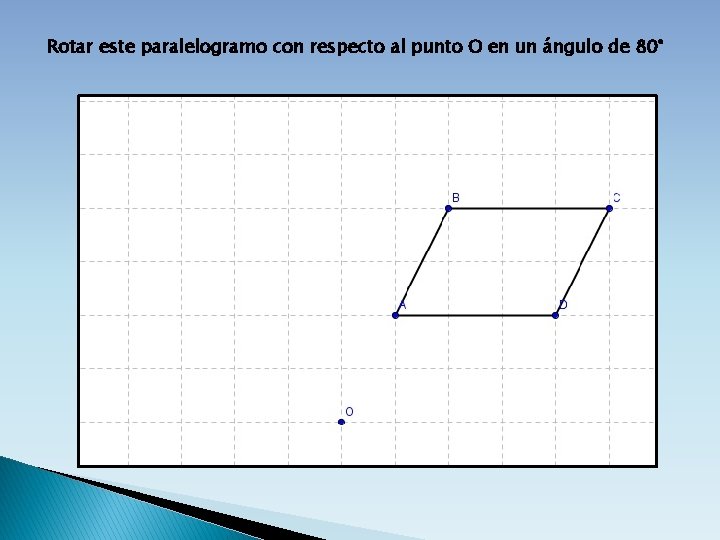
Rotar este paralelogramo con respecto al punto O en un ángulo de 80°

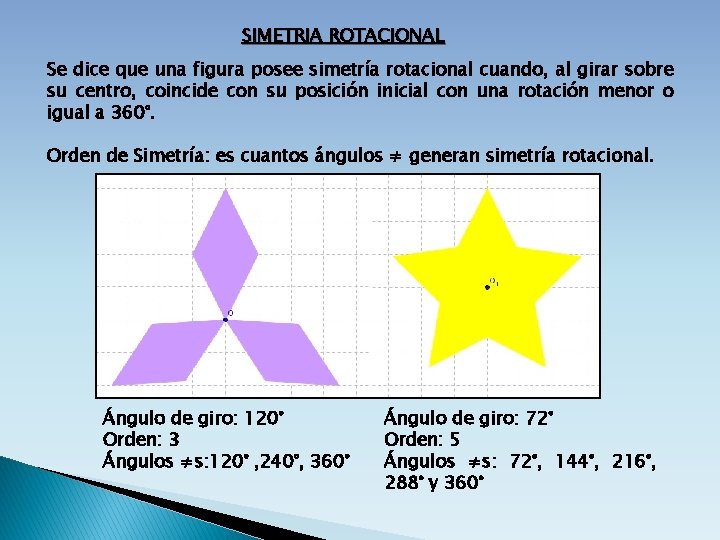
SIMETRIA ROTACIONAL Se dice que una figura posee simetría rotacional cuando, al girar sobre su centro, coincide con su posición inicial con una rotación menor o igual a 360°. Orden de Simetría: es cuantos ángulos ≠ generan simetría rotacional. Ángulo de giro: 120° Orden: 3 Ángulos ≠s: 120° , 240°, 360° Ángulo de giro: 72° Orden: 5 Ángulos ≠s: 72°, 144°, 216°, 288° y 360°

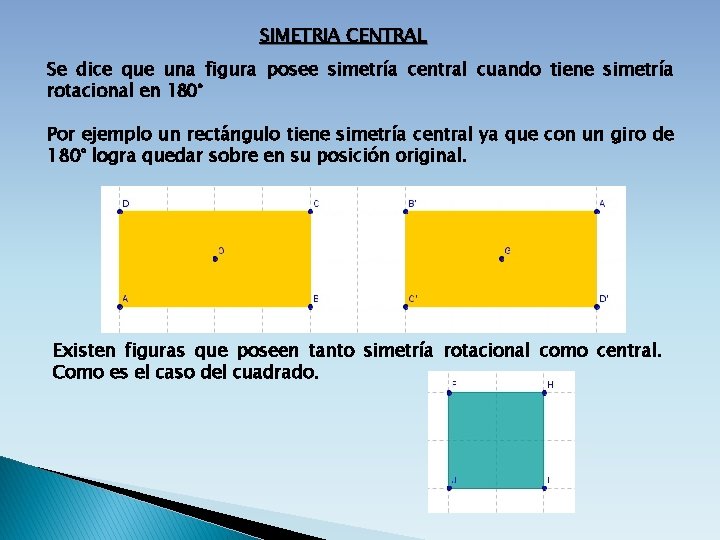
SIMETRIA CENTRAL Se dice que una figura posee simetría central cuando tiene simetría rotacional en 180° Por ejemplo un rectángulo tiene simetría central ya que con un giro de 180° logra quedar sobre en su posición original. Existen figuras que poseen tanto simetría rotacional como central. Como es el caso del cuadrado.

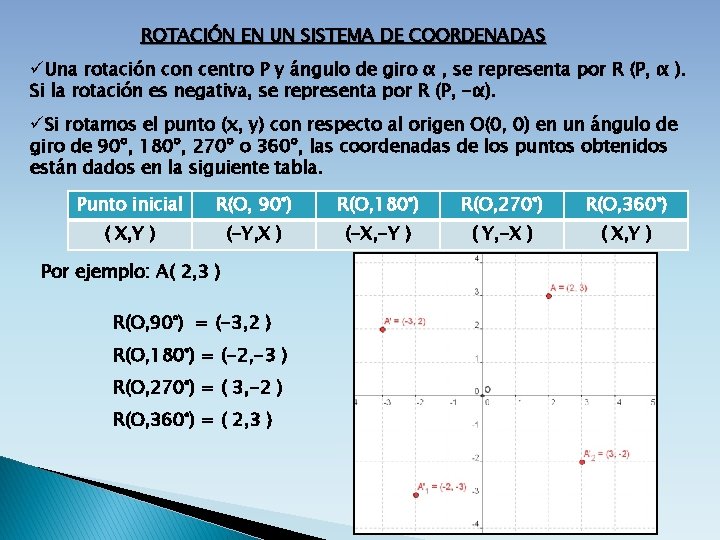
ROTACIÓN EN UN SISTEMA DE COORDENADAS üUna rotación con centro P y ángulo de giro α , se representa por R (P, α ). Si la rotación es negativa, se representa por R (P, -α). üSi rotamos el punto (x, y) con respecto al origen O(0, 0) en un ángulo de giro de 90º, 180º, 270º o 360º, las coordenadas de los puntos obtenidos están dados en la siguiente tabla. Punto inicial R(O, 90°) R(O, 180°) R(O, 270°) R(O, 360°) ( X, Y ) (-Y, X ) (-X, -Y ) ( Y, -X ) ( X, Y ) Por ejemplo: A( 2, 3 ) R(O, 90°) = (-3, 2 ) R(O, 180°) = (-2, -3 ) R(O, 270°) = ( 3, -2 ) R(O, 360°) = ( 2, 3 )

RESUMEN CLASE ANTERIOR Verifiquemos lo aprendido, indicando una definición para uno de los siguientes conceptos. v Rotación v Simetría rotacional v Simetría central v Rotación en un sistema de coordenadas v Ángulo y centro de rotación

Transformaciones Isométricas Traslaciones Rotaciones Simetría Rotacional Simetría Central Reflexiones Simetría axial Simetría Central

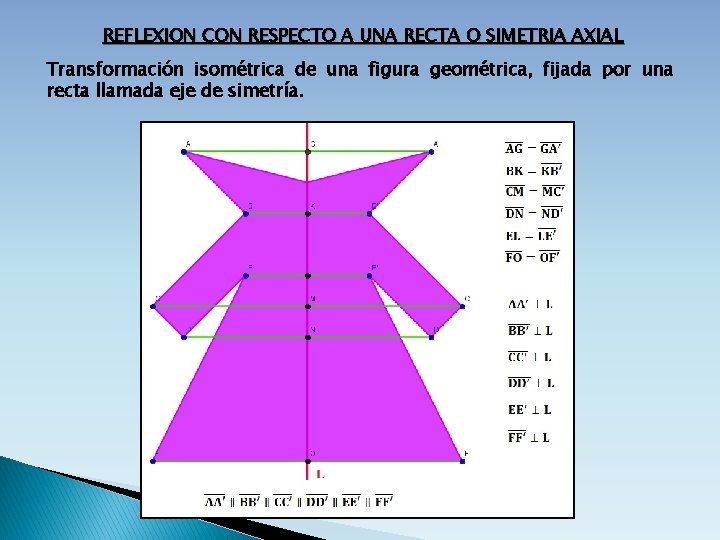
REFLEXION CON RESPECTO A UNA RECTA O SIMETRIA AXIAL Transformación isométrica de una figura geométrica, fijada por una recta llamada eje de simetría.

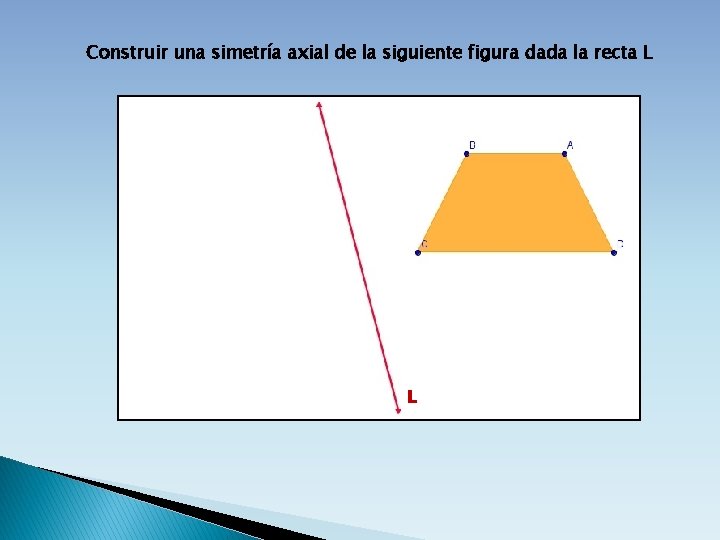
Construir una simetría axial de la siguiente figura dada la recta L L

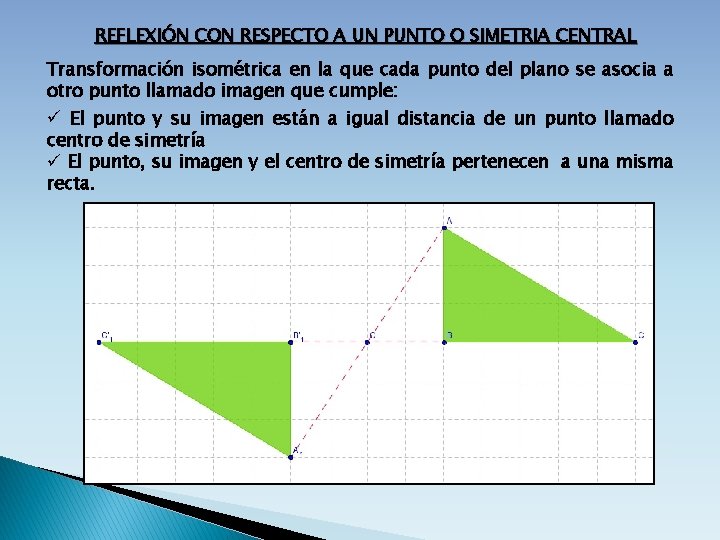
REFLEXIÓN CON RESPECTO A UN PUNTO O SIMETRIA CENTRAL Transformación isométrica en la que cada punto del plano se asocia a otro punto llamado imagen que cumple: ü El punto y su imagen están a igual distancia de un punto llamado centro de simetría ü El punto, su imagen y el centro de simetría pertenecen a una misma recta.

Construir una simetría central de la siguiente figura dado el punto O

SIMETRIA AXIAL EN UN SISTEMA DE COORDENADAS La simetría axial se puede representar en un sistema de coordenadas, dado un punto ( X , Y ) se puede encontrar su simétrico (X’, Y’). Punto Inicial Simétrico eje X Simétrico eje Y A( X, Y) A’( X, -Y ) A’’(-X, Y ) Por ejemplo: A(1, 1) A’(1, -1) A’’(-1, 1) B(1, 3) B’(1, -3) B’’(-1, 3) C(2, 4) C’(2, -4) C’’(-2, 4) D(4, 4) D’(4, -4) D’’(-4, 4)

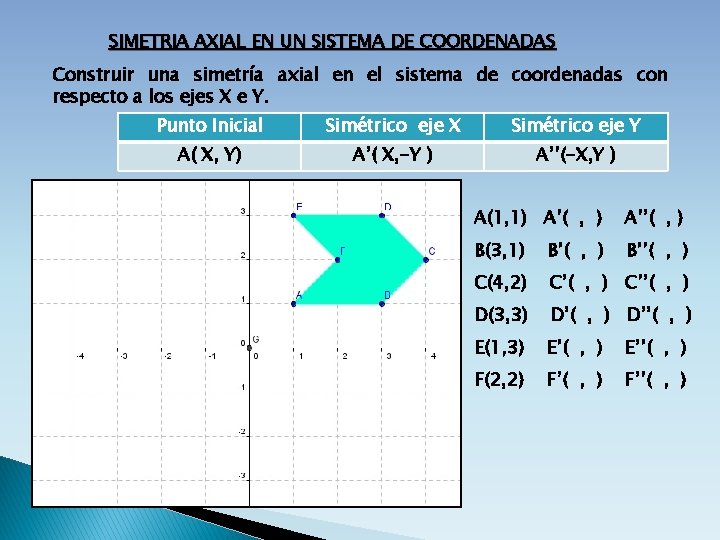
SIMETRIA AXIAL EN UN SISTEMA DE COORDENADAS Construir una simetría axial en el sistema de coordenadas con respecto a los ejes X e Y. Punto Inicial Simétrico eje X Simétrico eje Y A( X, Y) A’( X, -Y ) A’’(-X, Y ) A(1, 1) A’( , ) A’’( , ) B(3, 1) B’( , ) B’’( , ) C(4, 2) C’( , ) C’’( , ) D(3, 3) D’( , ) D’’( , ) E(1, 3) E’( , ) E’’( , ) F(2, 2) F’( , ) F’’( , )

SIMETRIA CENTRAL EN UN SISTEMA DE COORDENADAS La simetría central se puede representar en un sistema de coordenadas, dado un punto ( X , Y ) se puede encontrar su simétrico con respecto al origen (X’, Y’). Punto Inicial Simétrico punto O A( X, Y) Por ejemplo: Simetría axial con respecto a los ejes origen O. A(2, 1) B(1, 1) C(1, 3) D(2, 3) E(2, 4) F(3, 4) G(3, 2) A’(-2, -1) B’ (-1, -1) C’(-1, -3) D’(-2, -3) E’(-2, -4) F’(-3, -4) G’(-3, -2) A’( -X, -Y )

Construir una simetría central en el sistema de coordenadas con respecto al origen. Punto Inicial Simétrico punto O A( X, Y) A(1, 3) A’( , ) B(3, 4) B’( , ) C(5, 2) C’( , ) D(3, 1) D’( , ) A’( -X, -Y )

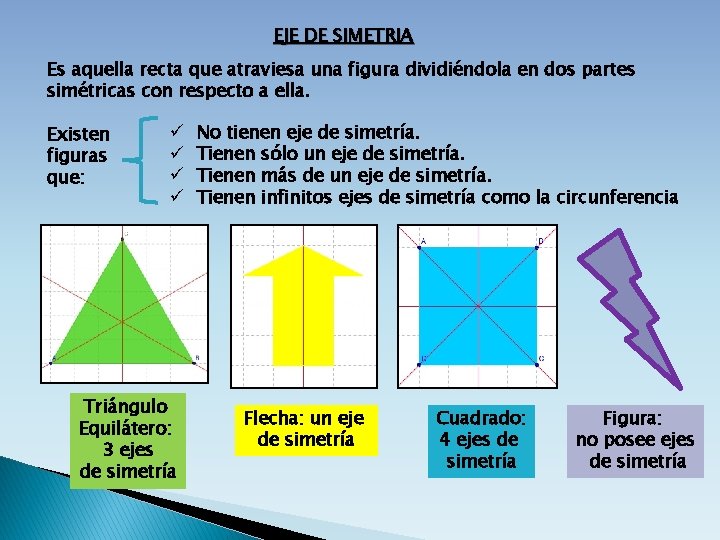
EJE DE SIMETRIA Es aquella recta que atraviesa una figura dividiéndola en dos partes simétricas con respecto a ella. Existen figuras que: ü ü Triángulo Equilátero: 3 ejes de simetría No tienen eje de simetría. Tienen sólo un eje de simetría. Tienen más de un eje de simetría. Tienen infinitos ejes de simetría como la circunferencia Flecha: un eje de simetría Cuadrado: 4 ejes de simetría Figura: no posee ejes de simetría
 Formas sustractivas
Formas sustractivas Hallar
Hallar Adifusional
Adifusional Transformaciones rigidas
Transformaciones rigidas Edades en que se divide la historia
Edades en que se divide la historia Cuales son las fuentes de las obligaciones mercantiles
Cuales son las fuentes de las obligaciones mercantiles Division de la prehistoria
Division de la prehistoria Tabla de compuertas logicas
Tabla de compuertas logicas Parte de un entero
Parte de un entero Recomendaciones de la tic
Recomendaciones de la tic Las once y cuarto
Las once y cuarto Propiedades constitutivas
Propiedades constitutivas Nueva cultura para todos
Nueva cultura para todos Diezmilesima
Diezmilesima Cuál es el objetivo de una leyenda
Cuál es el objetivo de una leyenda Que es una copla y sus características
Que es una copla y sus características Cuáles son las características de las emociones
Cuáles son las características de las emociones La parte de la semilla
La parte de la semilla Características de copla
Características de copla Mitos y leyendas diferencias
Mitos y leyendas diferencias Caracteristicas de una copla
Caracteristicas de una copla Pancreas histologia
Pancreas histologia Relieve islas baleares
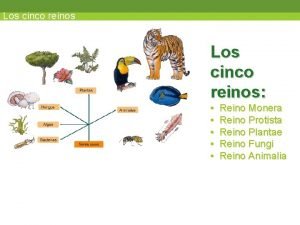
Relieve islas baleares Animalia plantae fungi protista y monera
Animalia plantae fungi protista y monera Las frutas son ________ (better) que las patatas fritas.
Las frutas son ________ (better) que las patatas fritas. Nosotros estudiantes de español
Nosotros estudiantes de español Versos de poemas ejemplos
Versos de poemas ejemplos 5 emociones negativas
5 emociones negativas Recursos literarios
Recursos literarios