Unidad IV Geometra TRANSFORMACIONES ISOMTRICAS LOS EJE DE

























- Slides: 40

Unidad IV : Geometría TRANSFORMACIONES ISOMÉTRICAS.

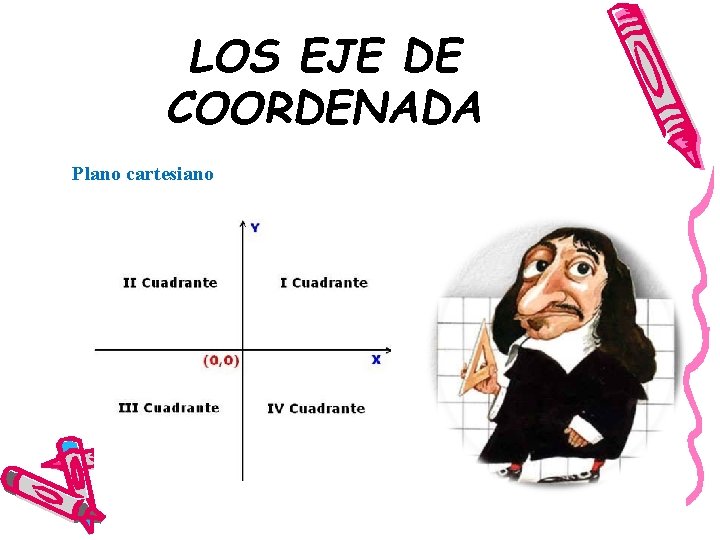
LOS EJE DE COORDENADA Plano cartesiano

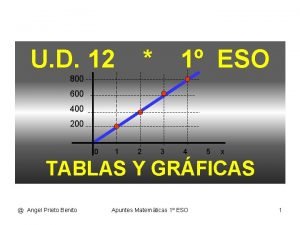
• El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.

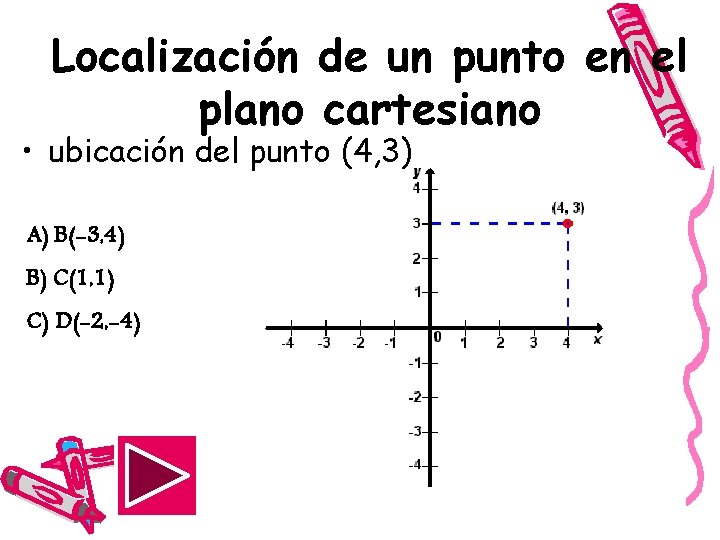
Localización de un punto en el plano cartesiano • ubicación del punto (4, 3) A) B(-3, 4) B) C(1, 1) C) D(-2, -4)

IGUAL MEDIDA

TRANSFORMACIONES ISOMÉTRICAS En una transformación isométrica: 1) No se altera la forma ni el tamaño de la figura. 2) Sólo cambia la posición (orientación o sentido de ésta).

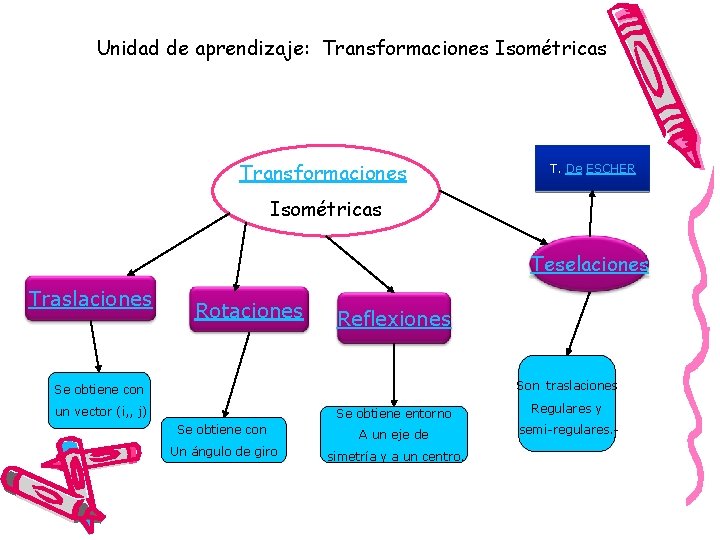
Unidad de aprendizaje: Transformaciones Isométricas Transformaciones T. De ESCHER Isométricas Teselaciones Traslaciones Rotaciones Reflexiones Son traslaciones Se obtiene con Se obtiene entorno Regulares y Se obtiene con A un eje de semi-regulares. - Un ángulo de giro simetría y a un centro. un vector (i, , j)

Tipos de transformaciones isométricas


Ejemplos de transformaciones isométricas en la naturaleza. -

SIMETRÍAS O REFLEXIONES Se puede considerar una simetría como aquel movimiento que aplicado a una figura geométrica, produce el efecto de un espejo.

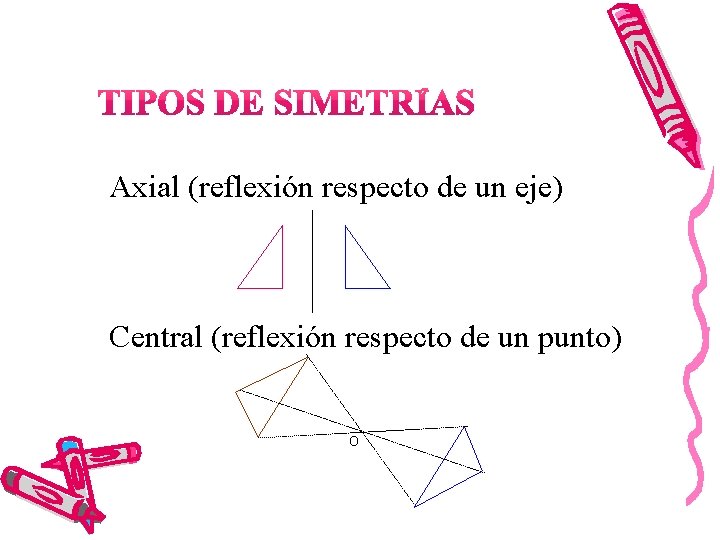
Axial (reflexión respecto de un eje) Central (reflexión respecto de un punto) O

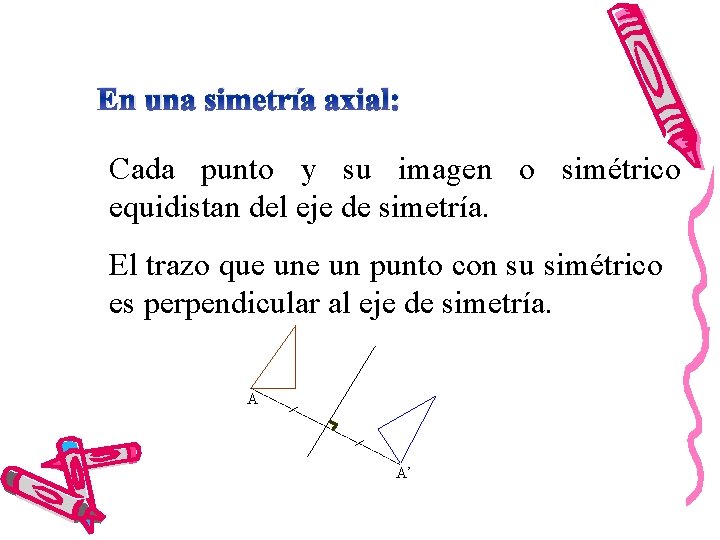
En una simetría axial: Cada punto y su imagen o simétrico equidistan del eje de simetría. El trazo que un punto con su simétrico es perpendicular al eje de simetría. A A’

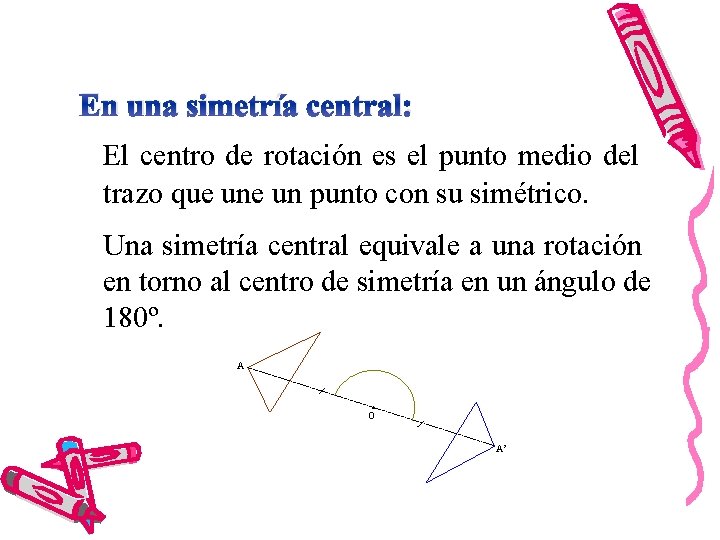
En una simetría central: El centro de rotación es el punto medio del trazo que un punto con su simétrico. Una simetría central equivale a una rotación en torno al centro de simetría en un ángulo de 180º. A O A’

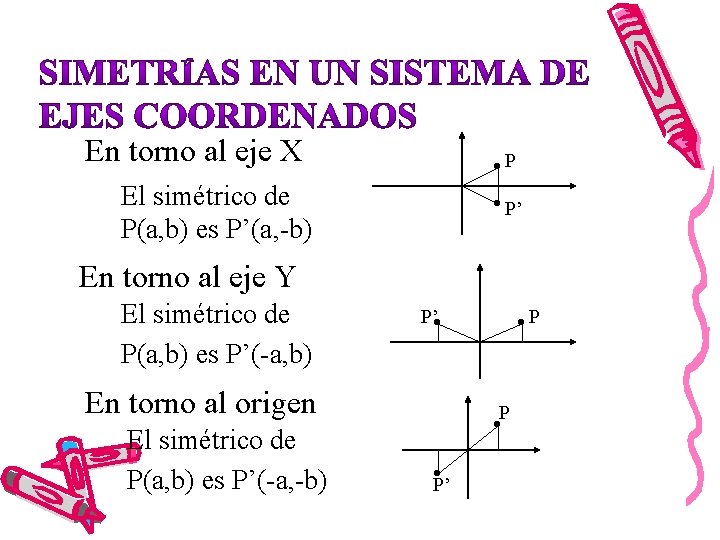
En torno al eje X P El simétrico de P(a, b) es P’(a, -b) P’ En torno al eje Y El simétrico de P(a, b) es P’(-a, b) P’ En torno al origen El simétrico de P(a, b) es P’(-a, -b) P P P’

Se puede considerar una traslación como el movimiento que se hace al deslizar una figura, en línea recta, manteniendo su forma y tamaño.

En una traslación: Al deslizar la figura todos los puntos describen líneas rectas paralelas entre sí.

En una traslación se distinguen tres elementos: Dirección (horizontal, vertical u oblicua). Sentido (derecha, izquierda, arriba, abajo). Magnitud del desplazamiento (distancia entre la posición inicial y final de cualquier punto)

En este caso se debe señalar las coordenadas del vector de traslación. Estas son un par ordenado de números (x, y), donde x representa el desplazamiento horizontal e y representa el desplazamiento vertical.

En el par ordenado la primera componente recibe el nombre de abscisa y la segunda componente el nombre de ordenada.

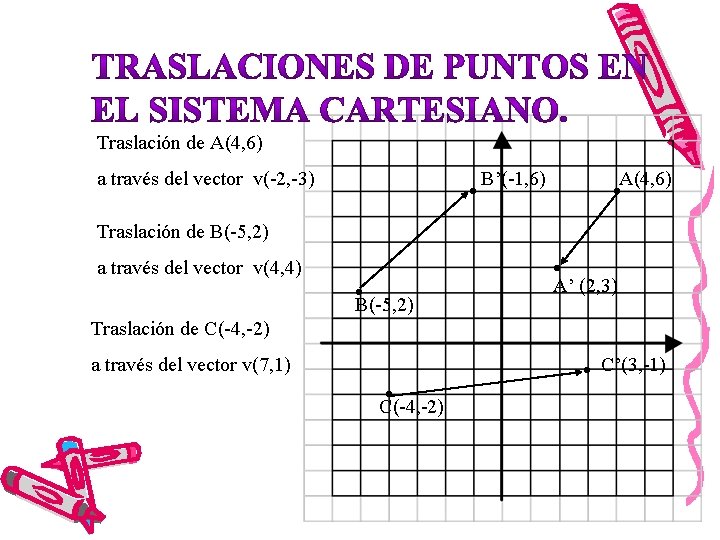
Traslación de A(4, 6) a través del vector v(-2, -3) B’(-1, 6) A(4, 6) Traslación de B(-5, 2) a través del vector v(4, 4) B(-5, 2) A’ (2, 3) Traslación de C(-4, -2) a través del vector v(7, 1) C’(3, -1) C(-4, -2)

En la abscisa: Signo positivo: desplazamiento hacia la derecha. Signo negativo: desplazamiento hacia la izquierda. En la ordenada: Signo positivo: desplazamiento hacia arriba. Signo negativo: desplazamiento hacia abajo.

Una rotación es el movimiento que se efectúa al girar una figura en torno a un punto. Este movimiento mantiene la forma y el tamaño de la figura.

En una rotación se identifican tres elementos: El punto de rotación (centro de rotación), punto en torno al cual se efectúa la rotación. La magnitud de rotación, que corresponde al ángulo, éste está determinado por un punto cualquiera de la figura, el centro de rotación (vértice del ángulo) y el punto correspondiente de la figura obtenida después de la rotación. El sentido de giro, positivo (antihorario), negativo (horario) N M M’ . O N’

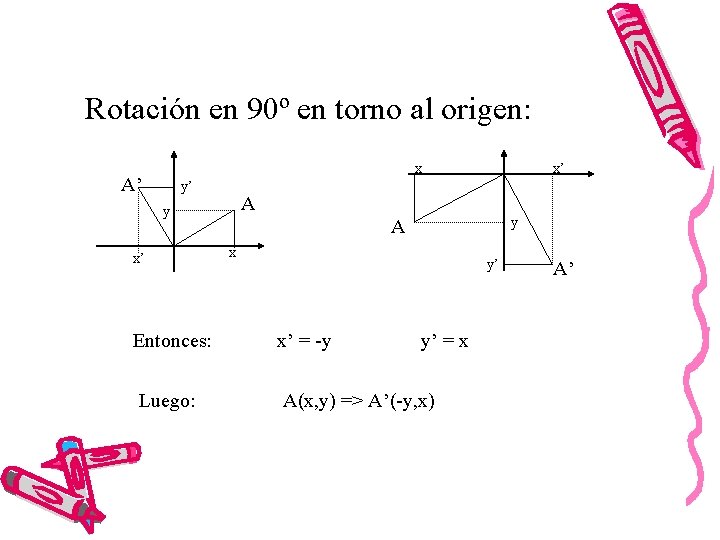
Rotación en 90º en torno al origen: x A’ y’ A y x’ x’ y A x y’ Entonces: x’ = -y y’ = x Luego: A(x, y) => A’(-y, x) A’

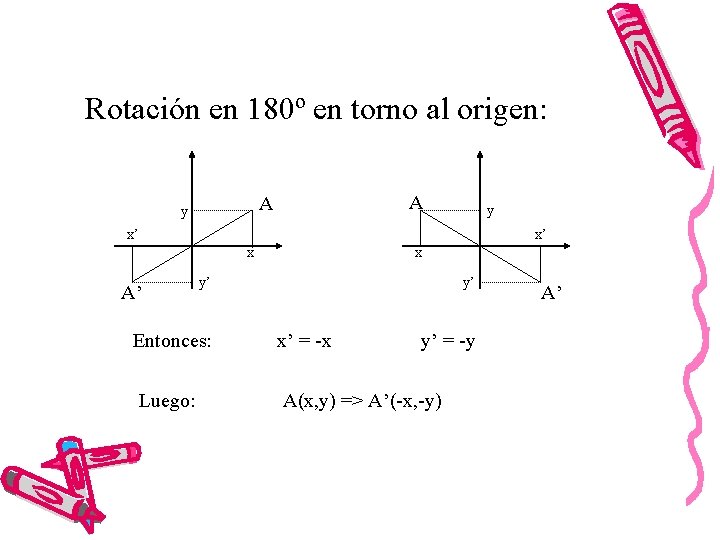
Rotación en 180º en torno al origen: A A y y x’ x’ x A’ x y’ y’ Entonces: x’ = -x y’ = -y Luego: A(x, y) => A’(-x, -y) A’

Importante Toda transformación isométrica, mantiene la forma y tamaño de una figura geométrica, por lo tanto el perímetro y el área no sufren variación.

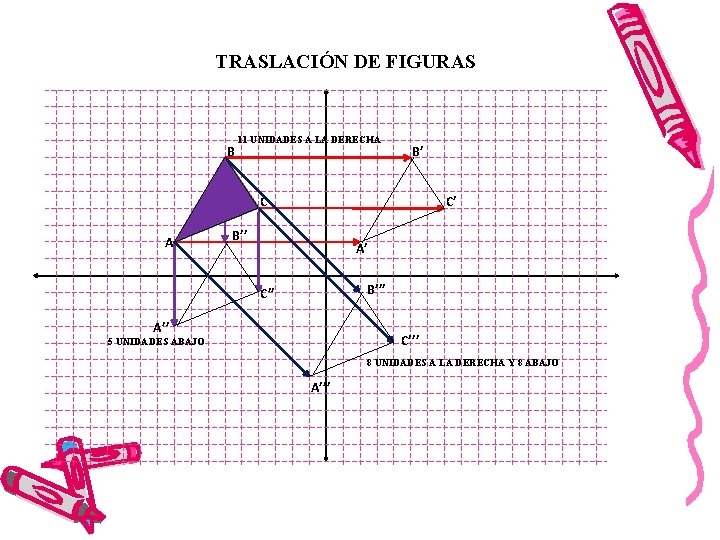
TRASLACIÓN DE FIGURAS B 11 UNIDADES A LA DERECHA B’ C A C’ B’’ A’ B’’’ C’’ A’’ C’’’ 5 UNIDADES ABAJO 8 UNIDADES A LA DERECHA Y 8 ABAJO A’’’

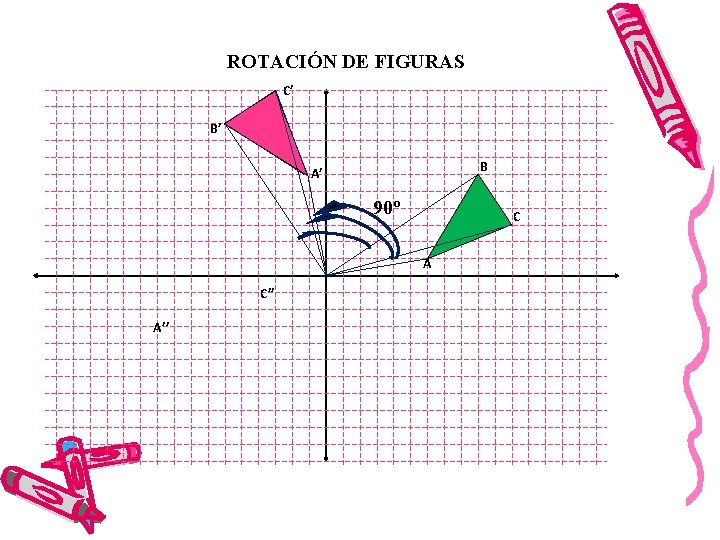
ROTACIÓN DE FIGURAS C’ B’ B A’ 90º C A C’’ A’’

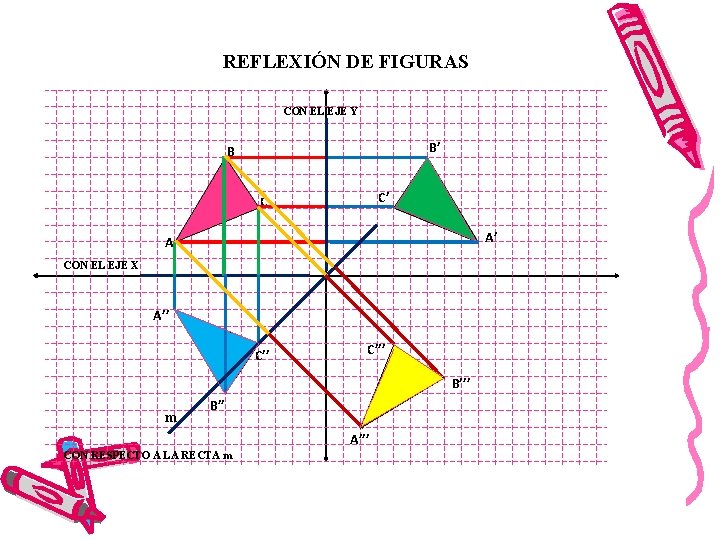
REFLEXIÓN DE FIGURAS CON EL EJE Y B’ B C’ C A’ A CON EL EJE X A’’ C’’’ B’’’ m B’’ A’’’ CON RESPECTO A LA RECTA m

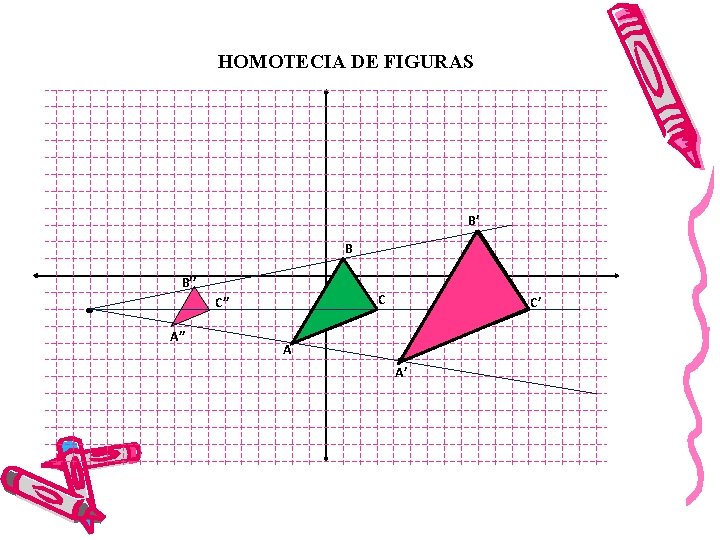
HOMOTECIA DE FIGURAS B’ B B’’ C C’’ A’’ C’ A A’


Teselaciones de • • Martin Cornelis ESCHER Hablar de Martin Cornelis Escher el cual fue un hombre dedicado al arte y que tenía el deseo de romper las limitaciones que impone el plano, para poder mostrar que un plano es capaz de ilusiones ópticas de gran profundidad. En la mezquita de Córdoba están sus obras para hacer aparecer en ellas dibujos matemáticos y por ello tuvo muchas críticas y comprendió que su audiencia no podía ser convencional, por lo que dijo: “A pesar de que no tengo ningun conocimiento ni enseñanza - de matemáticas -, habitualmente me parece que tengo más cosas en común con los matemáticos que con mis compañeros artistas”. Si observamos detalladamente alguna de sus obras podemos descubrir su dominio de la geometría. A Escher le maravillaba todo tipo de teselados, regulares o irregulares, y especialmente lo que él llamó “metamorfosis”, donde las figuras cambian e interactúan entre sí, y hasta a veces salen del plano.

Teselaciones de Escher • Realmente el trabajo, y las imágenes son extraordinarios! Que operan en el venerable principio de la stereopticon, estas cartas tienen un objetivo para cada ojo, una imagen casi idéntica para cada lente, y un agujero en el medio para dar cabida a la nariz. Usted ajustar el enfoque de apretar el plegado de las tarjetas.

Teselaciones de Escher


TESELACIONES DE ESCHER 37

38

Teselaciones de Escher y Aplicaciones • Transformador de Escher "se deriva de MC Escher del diseño de un pilar de hormigón pintada en el edificio de la Oficina de Gestión de los Recursos Hídricos en Haarlem, Países Bajos (1962). El diseño incorpora tres relacionados con el agua motivos (Simetría Nos 111, 112, 113) que flujo entre sí para crear una vertical de la metamorfosis "de vuelo de aves y peces" en "barco de vuelo y los peces" y, por último, en "barco y los peces".

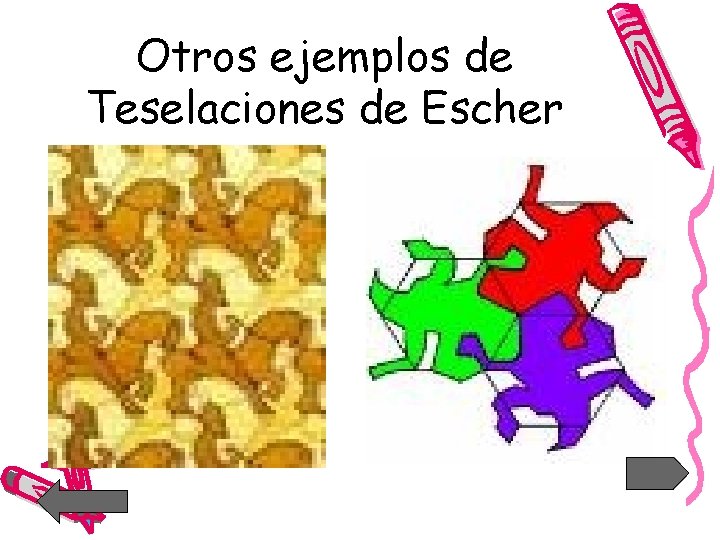
Otros ejemplos de Teselaciones de Escher
 Geometra significado
Geometra significado Que es geometra
Que es geometra Geometra significado
Geometra significado Angulo obtuso
Angulo obtuso La geometra
La geometra Geometra concept
Geometra concept Transformaciones sustractivas
Transformaciones sustractivas Hallar
Hallar Transformaciones adifusionales
Transformaciones adifusionales Transformaciones rigidas
Transformaciones rigidas Centenas decenas y unidades
Centenas decenas y unidades Los poligonos unidad 11
Los poligonos unidad 11 Eje de abscisas
Eje de abscisas Vector de traslacion formula
Vector de traslacion formula Planos corporales
Planos corporales Preguntas especificas
Preguntas especificas Pantalasso
Pantalasso Ejes centralizadores
Ejes centralizadores Que letra del abecedario no tiene eje de simetria
Que letra del abecedario no tiene eje de simetria Media luna fértil civilizaciones
Media luna fértil civilizaciones Eje focal vertical
Eje focal vertical Gurbansoltan eje etraby
Gurbansoltan eje etraby Teroja techaukarã
Teroja techaukarã Tiroides eje
Tiroides eje Estamento
Estamento Energia elica
Energia elica Relación entre la distancia focal y los semiejes
Relación entre la distancia focal y los semiejes Eje 2
Eje 2 La velocidad magnitud vectorial
La velocidad magnitud vectorial Punto coplanar
Punto coplanar Que son ajustes y tolerancias
Que son ajustes y tolerancias Diagnostico empresarial eje 4
Diagnostico empresarial eje 4 Ecuacion del eje focal
Ecuacion del eje focal Los polos en los imanes
Los polos en los imanes Recta paralela al eje y
Recta paralela al eje y Urlogo
Urlogo Aparsto reproductor masculino
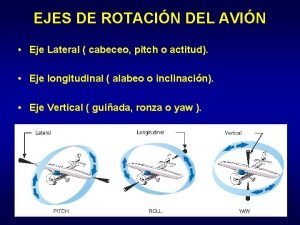
Aparsto reproductor masculino Eje de cabeceo
Eje de cabeceo Eje transversal del cuerpo humano
Eje transversal del cuerpo humano Figura formada por
Figura formada por Gurbansoltan eje etraby
Gurbansoltan eje etraby