1 CURVAS CNICAS Una Cnica es el conjunto



- Slides: 16

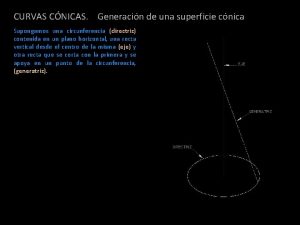
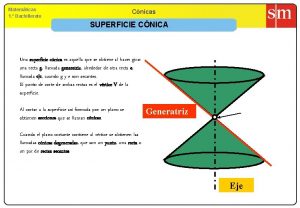
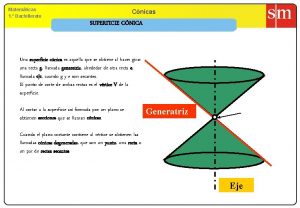
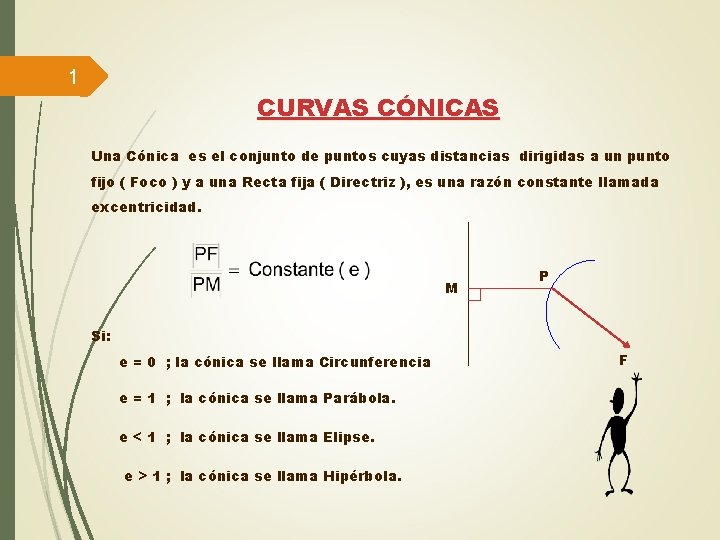
1 CURVAS CÓNICAS Una Cónica es el conjunto de puntos cuyas distancias dirigidas a un punto fijo ( Foco ) y a una Recta fija ( Directriz ), es una razón constante llamada excentricidad. M P Si: e = 0 ; la cónica se llama Circunferencia e = 1 ; la cónica se llama Parábola. e < 1 ; la cónica se llama Elipse. e > 1 ; la cónica se llama Hipérbola. F

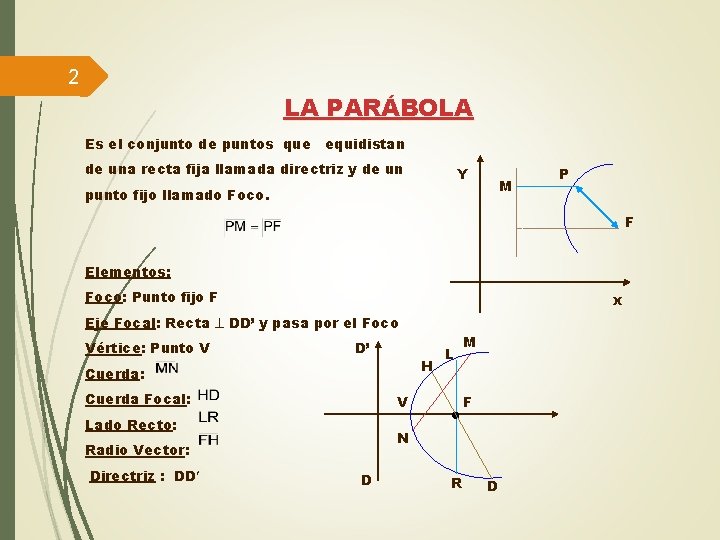
2 LA PARÁBOLA Es el conjunto de puntos que equidistan de una recta fija llamada directriz y de un Y M punto fijo llamado Foco. P F Elementos: Foco: Punto fijo F x Eje Focal: Recta DD’ y pasa por el Foco Vértice: Punto V D’ H Cuerda: Cuerda Focal: V Lado Recto: M F N Radio Vector: Directriz : DD L D R D

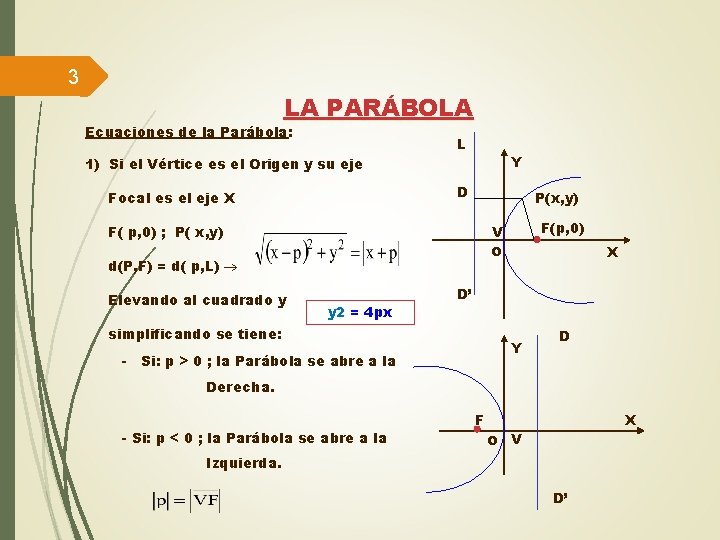
3 LA PARÁBOLA Ecuaciones de la Parábola: L Y 1) Si el Vértice es el Origen y su eje D Focal es el eje X P(x, y) F( p, 0) ; P( x, y) o d(P, F) = d( p, L) Elevando al cuadrado y F(p, 0) V y 2 = 4 px X D’ simplificando se tiene: Y - Si: p > 0 ; la Parábola se abre a la D Derecha. - Si: p < 0 ; la Parábola se abre a la F X o V Izquierda. D’

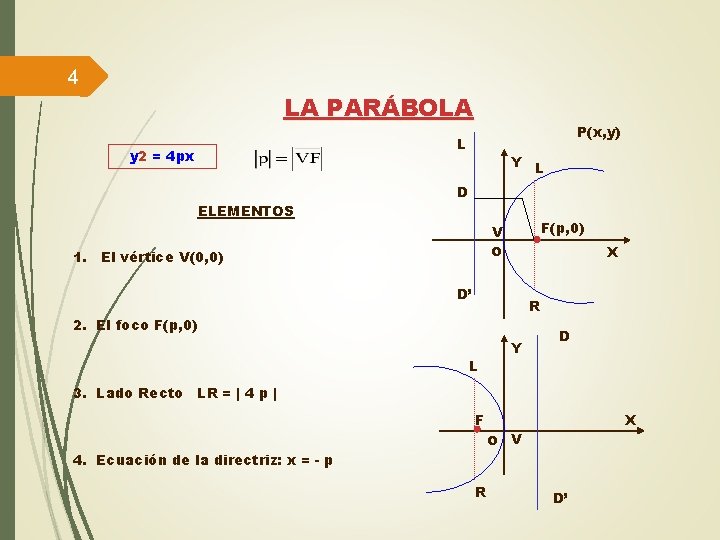
4 LA PARÁBOLA P(x, y) L y 2 = 4 px ELEMENTOS Y L D F(p, 0) V o 1. El vértice V(0, 0) X D’ R 2. El foco F(p, 0) L Y D 3. Lado Recto LR = | 4 p | F X o V 4. Ecuación de la directriz: x = - p R D’

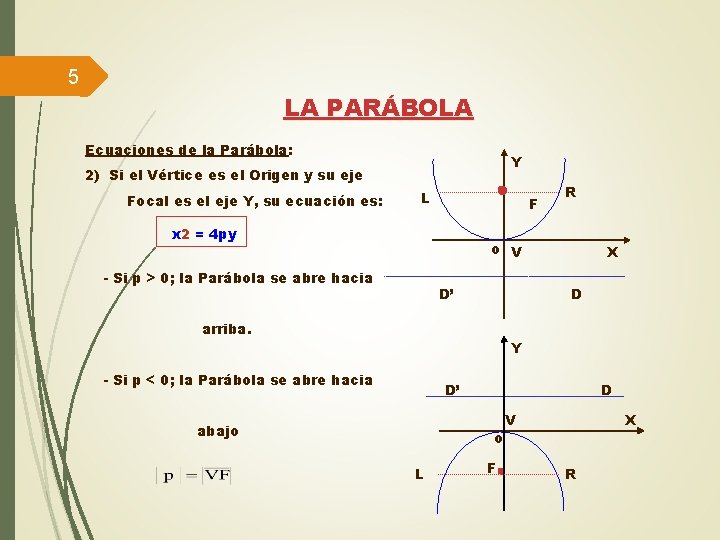
5 LA PARÁBOLA Ecuaciones de la Parábola: Y 2) Si el Vértice es el Origen y su eje Focal es el eje Y, su ecuación es: L F x 2 = 4 py R o V - Si p > 0; la Parábola se abre hacia D’ X D arriba. Y - Si p < 0; la Parábola se abre hacia D’ abajo D o L F V X R

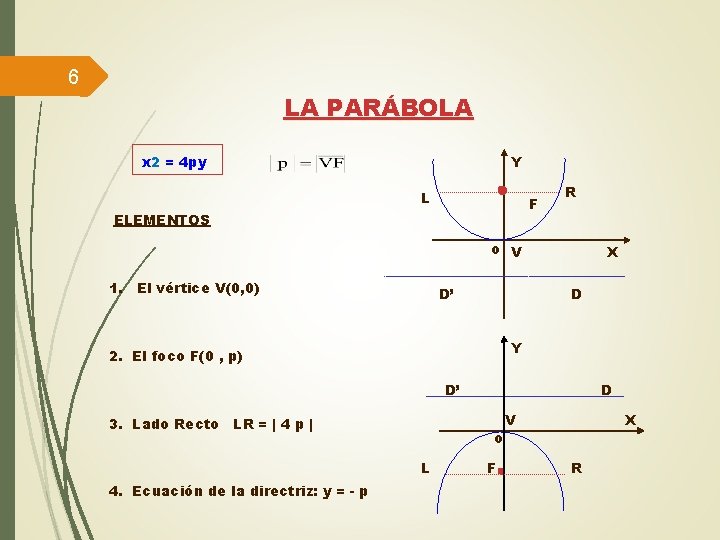
6 LA PARÁBOLA x 2 = 4 py Y L F ELEMENTOS R o V 1. El vértice V(0, 0) D’ X D Y 2. El foco F(0 , p) D’ 3. Lado Recto LR = | 4 p | o L 4. Ecuación de la directriz: y = - p D F V X R

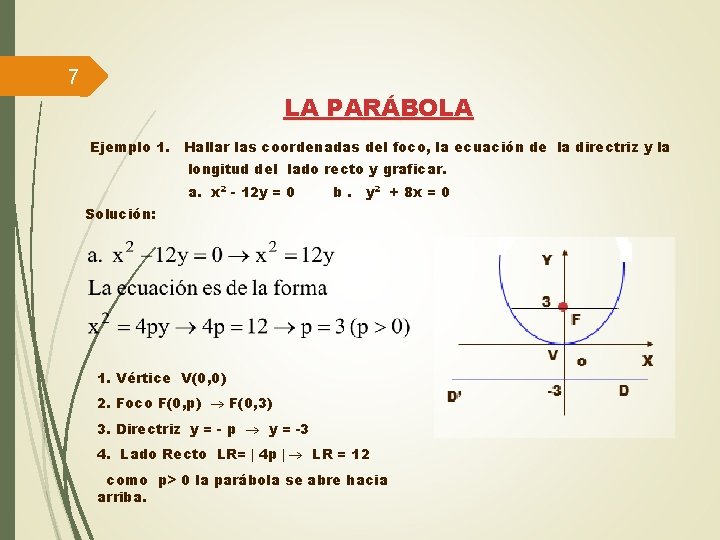
7 LA PARÁBOLA Ejemplo 1. Hallar las coordenadas del foco, la ecuación de la directriz y la longitud del lado recto y graficar. a. x 2 - 12 y = 0 b. y 2 + 8 x = 0 Solución: 1. Vértice V(0, 0) 2. Foco F(0, p) F(0, 3) 3. Directriz y = - p y = -3 4. Lado Recto LR= 4 p LR = 12 como p> 0 la parábola se abre hacia arriba.

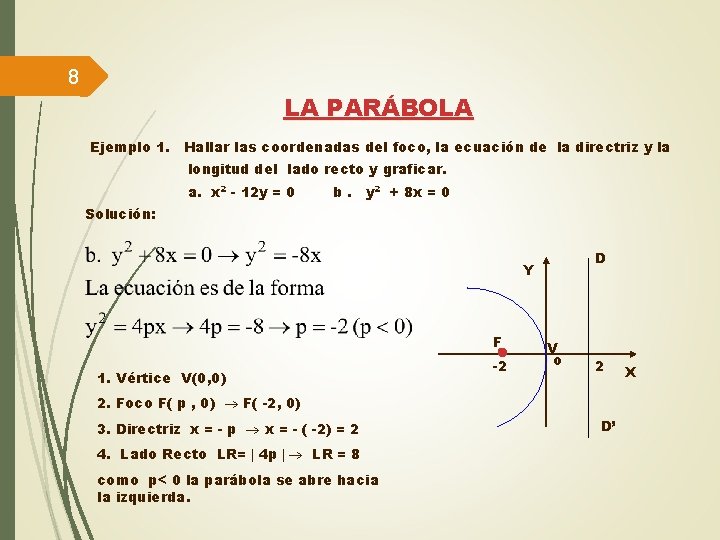
8 LA PARÁBOLA Ejemplo 1. Hallar las coordenadas del foco, la ecuación de la directriz y la longitud del lado recto y graficar. a. x 2 - 12 y = 0 b. y 2 + 8 x = 0 Solución: D Y F 1. Vértice V(0, 0) -2 V o 2 2. Foco F( p , 0) F( -2, 0) 3. Directriz x = - p x = - ( -2) = 2 4. Lado Recto LR= 4 p LR = 8 como p< 0 la parábola se abre hacia la izquierda. D’ X

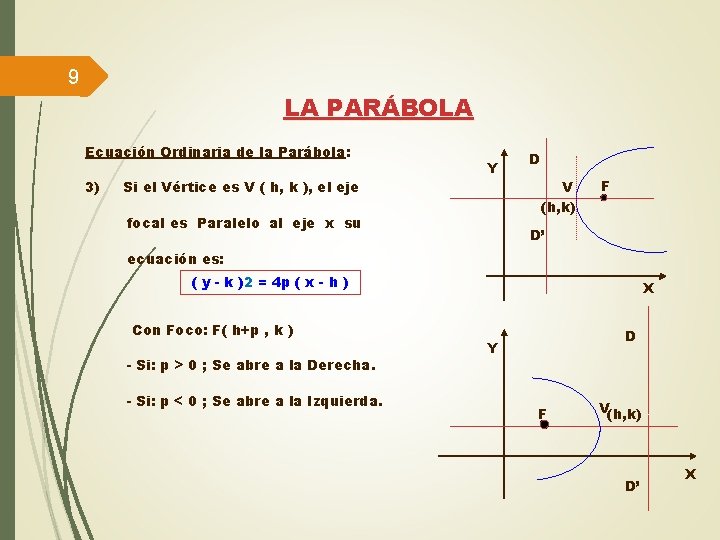
9 LA PARÁBOLA Ecuación Ordinaria de la Parábola: 3) Si el Vértice es V ( h, k ), el eje Y focal es Paralelo al eje x su D V (h, k) F D’ ecuación es: ( y - k )2 = 4 p ( x - h ) Con Foco: F( h+p , k ) - Si: p > 0 ; Se abre a la Derecha. - Si: p < 0 ; Se abre a la Izquierda. X D Y F V(h, k) D’ X

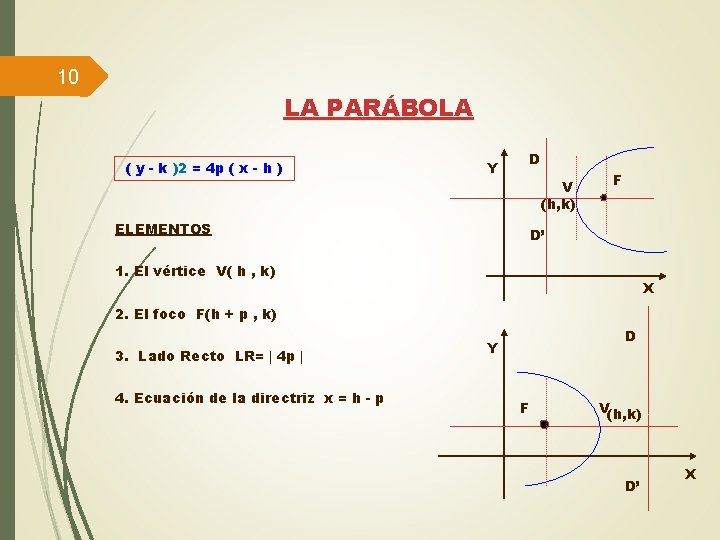
10 LA PARÁBOLA ( y - k )2 = 4 p ( x - h ) Y D V (h, k) ELEMENTOS F D’ 1. El vértice V( h , k) X 2. El foco F(h + p , k) 3. Lado Recto LR= 4 p 4. Ecuación de la directriz x = h - p D Y F V(h, k) D’ X

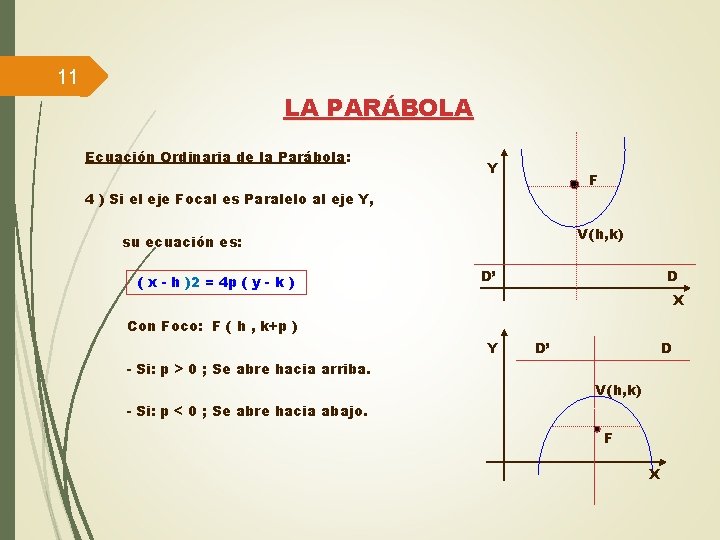
11 LA PARÁBOLA Ecuación Ordinaria de la Parábola: Y F 4 ) Si el eje Focal es Paralelo al eje Y, V (h, k) su ecuación es: ( x - h )2 = 4 p ( y - k ) D’ D X Con Foco: F ( h , k+p ) Y D’ D - Si: p > 0 ; Se abre hacia arriba. V (h, k) - Si: p < 0 ; Se abre hacia abajo. F X

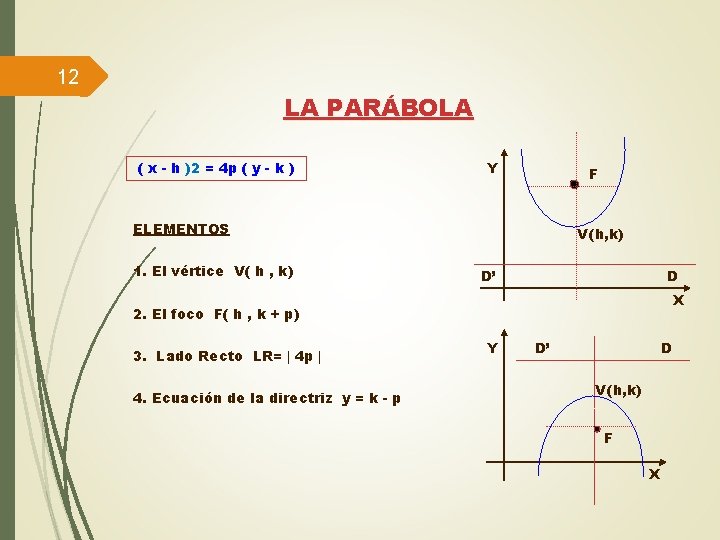
12 LA PARÁBOLA ( x - h )2 = 4 p ( y - k ) Y F ELEMENTOS 1. El vértice V( h , k) V (h, k) D’ D X 2. El foco F( h , k + p) 3. Lado Recto LR= 4 p 4. Ecuación de la directriz y = k - p Y D’ D V (h, k) F X

13 LA PARÁBOLA 5. La Ecuación General de la Parábola esta dado por: x 2 + Dx + Ey + F = 0 ; Si tiene eje focal paralelo al eje Y. y 2 + Dx + Ey + F = 0 ; Si tiene eje focal paralelo al eje X. Ejemplo 1. Hallar la ecuación de la parábola cuyos vértices y focos son los puntos (-4, 3) y (-1 , 3) respectivamente. Hallar también las ecuaciones de su directriz , eje focal y LR. Solución: La parábola es de la forma: V F 3 (y - k)2 = 4 p(x - h) -4 Directriz: x = h - p =-4 -3 =-7 x+7=0 Eje de la parábola y=k y = 3 , LR = 12 -1

14 LA PARÁBOLA Ejemplo 2. Hallar la ecuación de la parábola cuyo vértice y foco son los puntos V (3 , 3 ) y F(3 , 1 ) respectivamente. Hallar también las ecuaciones de su directriz , eje focal y LR. Solución: La parábola es de la forma: (x - h)2 = 4 p(y –k ) V L R o Directriz: y = k - p = 3 – (-2) = 5 y – 5 = 0 Eje de la parábola x = 3 x – 3 = 0 LR = 8 F

15 LA PARÁBOLA Ejemplo 3. Hallar las coordenadas del vértice y del foco. Las ecuaciones de la directriz y eje, y la longitud del lado recto. 4 x 2 + 48 y + 12 x – 159 =0 Solución: Completando cuadrados para la variable x, se tiene: De donde h = -3/2 , k = 7/2 , 4 p = -12 , p= -3 Vértice V( h , k) V( - 3/2 , 7/2 ) Foco F( h , k + p ) F( -3/2 , 7/2 – 3 ) F( -3/2 , 1/2 ) Ec. De la directriz: y = k - p y = 7/2 + 3 y = 1 3 / 2 2 y – 13 = 02 Ec del eje : x = h x = -3/2 2 x + 3 = 0 ; LR = 12

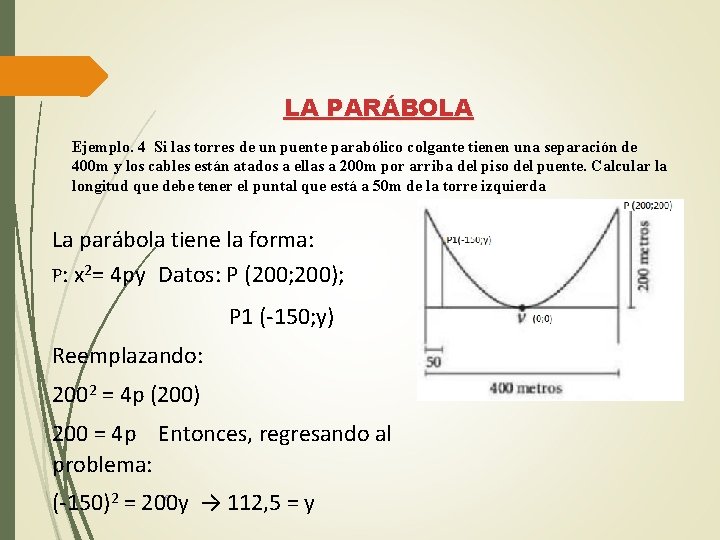
LA PARÁBOLA Ejemplo. 4 Si las torres de un puente parabólico colgante tienen una separación de 400 m y los cables están atados a ellas a 200 m por arriba del piso del puente. Calcular la longitud que debe tener el puntal que está a 50 m de la torre izquierda La parábola tiene la forma: P: x 2= 4 py Datos: P (200; 200); P 1 (-150; y) Reemplazando: 2002 = 4 p (200) 200 = 4 p Entonces, regresando al problema: (-150)2 = 200 y → 112, 5 = y 16
 Curvas y mapas de indiferencia
Curvas y mapas de indiferencia Curvas de schade
Curvas de schade Cerchas combinadas
Cerchas combinadas Curvas de indiferencia atipicas
Curvas de indiferencia atipicas Restricción presupuestaria fórmula
Restricción presupuestaria fórmula Curvas cot adn
Curvas cot adn Curvas en el espacio
Curvas en el espacio Area entre dos curvas
Area entre dos curvas Um recipiente termicamente isolado contém 500g de água
Um recipiente termicamente isolado contém 500g de água Curvas características
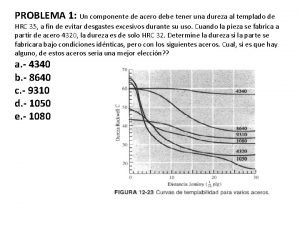
Curvas características Curvas de templabilidad
Curvas de templabilidad Insulinas curvas
Insulinas curvas Curvas cor
Curvas cor Conicas en la vida real
Conicas en la vida real Curvas de flujo
Curvas de flujo Qumica
Qumica Solubilidad
Solubilidad