Curvas en el espacio y funciones vectoriales En

Curvas en el espacio y funciones vectoriales En la sección de curvas paramétricas definimos una curva C en el plano como un conjunto de pares ordenados (f (t), g (t)) junto con unas ecuaciones paramétricas x = f (t) e y = g (t); donde f y g son funciones continuas de t en un intervalo I. esta definición admite una extensión natural al espacio tridimensional, como sigue. Una curva C en el espacio es un conjunto de tripletas ordenadas (f (t), g (t), h (t)) junto con unas ecuaciones paramétricas x = f (t) , y = g (t) y z = h (t) Donde f , g y h denotan funciones continuas de t en un intervalo I. Antes de ver algunos ejemplos de curvas en el espacio, introduciremos un nuevo tipo de funciones, las funciones vectoriales. Aplican los números reales en vectores, es decir, son funciones con valores vectoriales.

DEFINICIÓN DE FUNCIONES VECTORIALES Se llama función vectorial a cualquier función de la forma r(t) = f(t)i + g(t)j + h(t)k Plano Espacio donde las funciones componentes f, g y h son funciones del parámetro t con valores reales. Las funciones vectoriales se denotan con frecuencia por: r(t) = <f(t) , g(t)> r(t) = <f(t) , g(t) , h(t)>

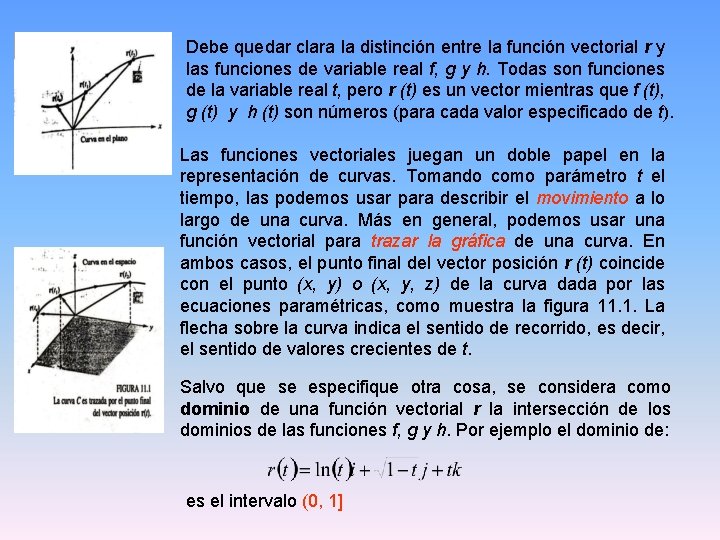
Debe quedar clara la distinción entre la función vectorial r y las funciones de variable real f, g y h. Todas son funciones de la variable real t, pero r (t) es un vector mientras que f (t), g (t) y h (t) son números (para cada valor especificado de t). Las funciones vectoriales juegan un doble papel en la representación de curvas. Tomando como parámetro t el tiempo, las podemos usar para describir el movimiento a lo largo de una curva. Más en general, podemos usar una función vectorial para trazar la gráfica de una curva. En ambos casos, el punto final del vector posición r (t) coincide con el punto (x, y) o (x, y, z) de la curva dada por las ecuaciones paramétricas, como muestra la figura 11. 1. La flecha sobre la curva indica el sentido de recorrido, es decir, el sentido de valores crecientes de t. Salvo que se especifique otra cosa, se considera como dominio de una función vectorial r la intersección de los dominios de las funciones f, g y h. Por ejemplo el dominio de: es el intervalo (0, 1]

(Trazado de una curva en el plano) EJEMPLO 1: Dibujar la curva representada por la función vectorial Solución:

(Tazado de una curva en el espacio) EJEMPLO 2: Dibujar la curva representada por la función vectorial Solución: Esto significa que la curva está en un cilindro circular recto de radio 4, centrado en el eje z. Para localizar la curva en ese cilindro podemos usar la tercera ecuación paramétrica z = t. Obsérvese, en la figura de la pizarra, que cuando t crece de 0 a 4π el punto (x, y, z) se mueve en espiral hacia arriba, describiendo una hélice

EJEMPLO 3: Hallar una función vectorial que represente una gráfica dada por: x = 2 + t, y = 3 t y z=4 -t Claro está que si la gráfica se da en forma paramétrica, la respuesta es inmediata. Así, para representar la recta dada en el espacio basta utilizar la función vectorial r (t) = (2 + t)i + 3 tj + (4 – t)k Si no se da un conjunto de ecuaciones paramétricas para la gráfica en cuestión, el problema de representarla mediante una función vectorial se reduce al de hallar un conjunto de ecuaciones paramétricas