INTEGRALES de FUNCIONES VECTORIALES INTRODUCCIN Sea C una

INTEGRALES de FUNCIONES VECTORIALES INTRODUCCIÓN: Sea C una curva suave definida por la función vectorial : [a ; b]→ 2 , con f e g funciones continuas t [a; b], las primitivas (o antiderivadas) de son funciones vectoriales y la integral indefinida es una familia de funciones vectoriales. Dado que las funciones componentes de son funciones escalares, la integral indefinida de puede obtenerse a partir de las integrales indefinidas de sus funciones componentes. Luego:

La integral definida de la función vectorial en [a; b] es un vector y puede obtenerse integrando cada una de sus funciones componentes y luego evaluando en los extremos. Haciendo extensivos los Teoremas Fundamentales del Cálculo Integral para funciones vectoriales y aplicando a continuación la Regla de Barrow: Donde es una primitiva de , es decir t [a; b] Reemplazando llegamos a: Es decir que el resultado de integrar la razón de cambio instantánea de cuando t varía desde a hasta b es el cambio total de para ese mismo intervalo.

INTEGRAL de FUNCIONES VECTORIALES – CAMBIO TOTAL * Si , es la función de posición de un objeto que se mueve en el plano con t t 1 ; t 2 , entonces su velocidad es Por lo tanto, es el “cambio total de posición” ó “desplazamiento total” ( ∆x; ∆y ) entre t 1 y t 2 Conocida la función velocidad, ¿Cuál es la posición del móvil en cada instante? NO

¿Condición inicial? Una partícula comienza su movimiento siendo su posición inicial con una velocidad. Determina la velocidad inicial, posición y aceleración en cada instante. A=1; B=1

Recuerdo: DEFINICIÓN

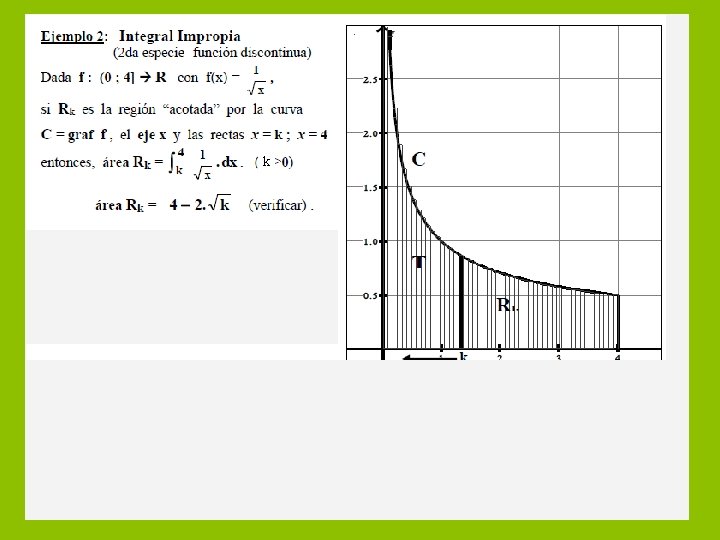
T R Integrales impropias

Teorema 1: Sea f continua en [a; b] entonces f es integrable en [a; b] T 2: Sea f seccionalm. continua en [a; b] entonces f es integrable en [a; b] 1. - El intervalo de integración no es acotado; tiene la forma: [a ; + ) ó (- ; b] ó (- ; + ) 2. - El integrando tiene una discontinuidad infinita en algún punto c : INTEGRALES IMPROPIAS

k