Graficacin IA 7200 T Algoritmos Clsicos Una Lnea

Graficación IA 7200 -T Algoritmos Clásicos

Una Línea Ideal • Solo podemos lograr una aproximación • Iluminar pixeles tan cerca a la línea ideal como sea posible – Pixel e {0, 1} Graficación 2

Linea Ideal • Recta y continua – Solo es posible a 0 y 45 o • Se debe interpolar • Debe ser eficiente – Se requiere dibujar muchas!!! Graficación 3

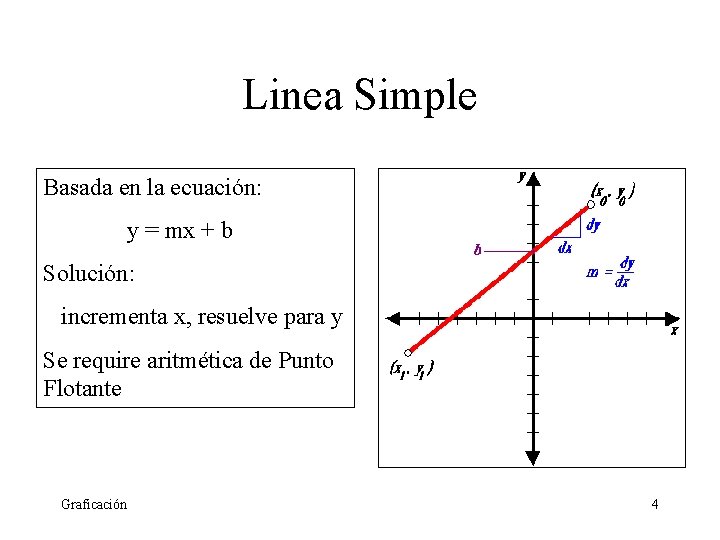
Linea Simple Basada en la ecuación: y = mx + b Solución: incrementa x, resuelve para y Se require aritmética de Punto Flotante Graficación 4

Funciona? Sí, para líneas con m<=1. Si m>1, la línea se hace muy discontinua. Se requiere mas de 1 pixel por columna Solución? - simetría. Graficación 5

Modificar algoritmo por octante o incrementar en x si dy<dx, si no, incrementar en y Graficación 6

Algoritmo DDA • DDA = Digital Differential Analyser – Differencias finitas • Tratar la linea como una ecuación paramétrica en t : Inicio Fin - Graficación 7

Algoritmo DDA • • Empezar en t = 0 En cada paso, incrementar t en dt Elegir un valor para dt Asegurar que se nos pasan pixeles: – Implica y • dt = maximum(dx, dy) Graficación 8

Algoritmo DDA line(int x 1, int y 1, int x 2, int y 2) { float x, y; int dx = x 2 -x 1, dy = y 2 -y 1; int n = max(abs(dx), abs(dy)); float dt = n, dxdt = dx/dt, dydt = dy/dt; x = x 1; y = y 1; while( n-- ) { point(round(x), round(y)); x += dxdt; y += dydt; } } Graficación n – rango de t. 9

Algoritmo DDA • Aun se necesitan muchas operaciones de PF. – 2 ‘round’s y 2 adds por pixel. • Hay una manera más simple? • Podemos usar solo aritmética entera? – Mas fácil de implementar en hardware Graficación 10

Observación en Líneas while( n-- ) { draw(x, y); move right; if( below line ) move up; } Graficación 11

Arriba o Debajo de la Línea? • Test para pixel • Escribir la línea en forma implícita: • F<0 para puntos arriba de la línea, F>0 para puntos debajo. Graficación 12

Testing for the side of a line. • Need to find coefficients a, b, c. • Recall explicit, slope-intercept form : • So: Graficación 13

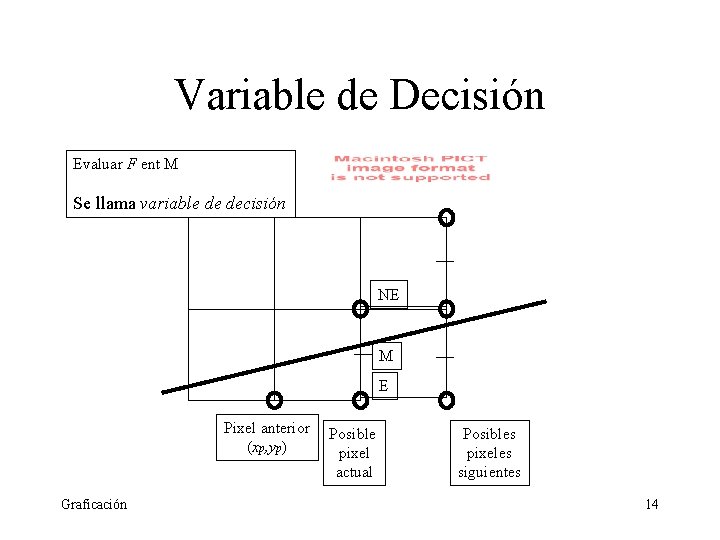
Variable de Decisión Evaluar F ent M Se llama variable de decisión NE M E Pixel anterior (xp, yp) Graficación Posible pixel actual Posibles pixeles siguientes 14

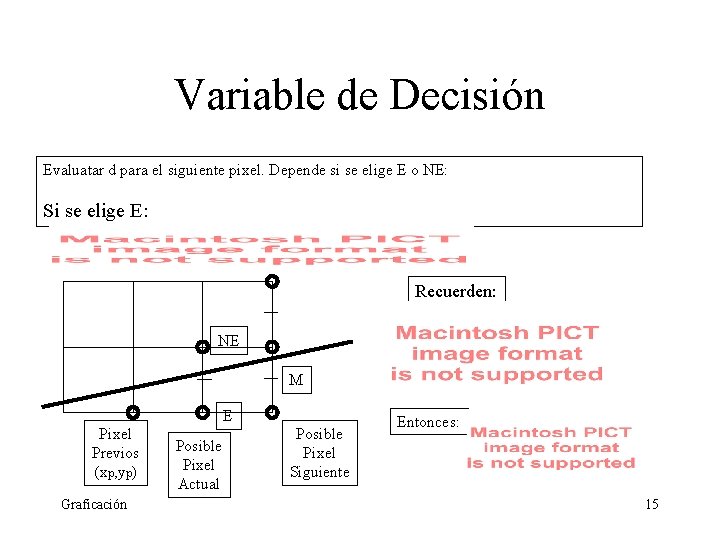
Variable de Decisión Evaluatar d para el siguiente pixel. Depende si se elige E o NE: Si se elige E: Recuerden: NE M E Pixel Previos (xp, yp) Graficación Posible Pixel Actual Posible Pixel Siguiente Entonces: 15

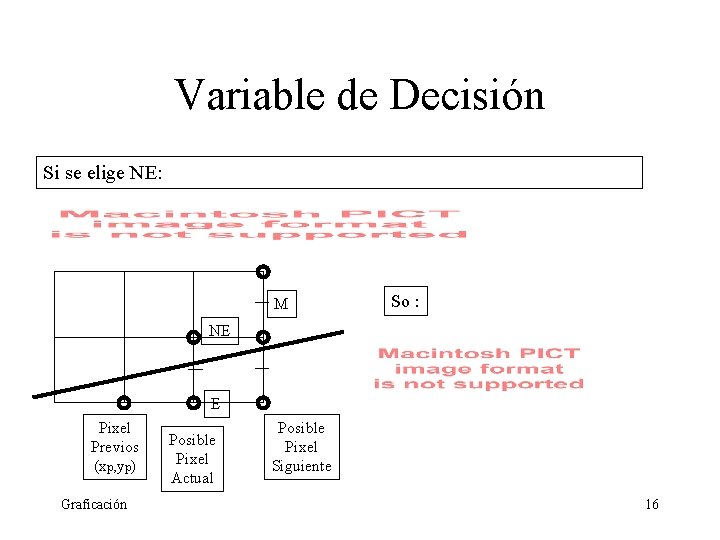
Variable de Decisión Si se elige NE: M So : NE E Pixel Previos (xp, yp) Graficación Posible Pixel Actual Posible Pixel Siguiente 16

Resumen del Algoritmo de Punto Medio • Elegir entre 2 pixelse en cada iteración, dependiendo del signo de la var. de decisión • Atualizar la variable de decisión dependiendo de que pixel es elegido • Comenzar en (x 1, y 1) • Calcular en valor inicial de d Graficación 17

Valor Inicial de d Inicioo: (x 1, y 1) Pero (x 1, y 1) es un punto en la línea, F(x 1, y 1) =0 Multiplicar por 2 para remover la fracción no afecta el signo Graficación 18

Algoritmo de Bresenham void Midpoint. Line(int x 1, y 1, x 2, y 2) { int dx=x 2 -x 1; int dy=y 2 -y 1; int d=2*dy-dx; int incre. E=2*dy; int incr. NE=2*(dy-dx); x=x 1; y=y 1; Write. Pixel(x, y); Graficación while (x < x 2) { if (d<= 0) { d+=incr. E; x++ } else { d+=incr. NE; x++; y++; } Write. Pixel(x, y); } } 19

Bresenham no fue el final! Algoritmo doble de Xiaolin Wu: El programa de dibujado es un autómata (máquina de estados finitos). i. e. Checar los siguientes dos pixeles de la línea. Solo existen un número finito (pequeño) de posibilidades. El algoritmo doble explota simetría dibujando simultáneamente de ambos extremos hacia el centro. Graficación 20

Algoritmo Doble Las posiciones posibles de los dos pixeles siguientes dependen de la pendiente – pixel actual en azul: 0<=m<=½ ½<=m<=1 1<=m<=2 m>2 Graficación 21

Círculos • Podemos usar Bresenham para círculos • Usar simetría 8 -tuple E M SE Pixel Previos Graficación Posible Pixel Actual Posible Pixel Siguiente 22

Círculos • La forma Implícita de un círculo es: Las Funciones son ecuaciones lineales en términos de (xp, yp) –Llamado punto de evaluación Graficación 23