La Transformada z Definicin de la transformada z
![La Transformada z Por conveniencia, la transformada z de x[n] se denota algunas veces](https://slidetodoc.com/presentation_image/1f9eea625e8570fbdf9b6034bc8aa9cf/image-3.jpg "La Transformada z Por conveniencia, la transformada z de x[n] se denota algunas veces")
- Slides: 56
La Transformada z Definición de la transformada z Propiedades y transformadas comunes Representación de sistemas LTI de tiempo discrete mediante la transformada z Función de transferencia de sistemas de tiempo discreto
La Transformada z •
La Transformada z Por conveniencia, la transformada z de x[n] se denota algunas veces como Z{x[n]} y la relación entre x[n] y su transformada z se indica como Anteriormente examinamos varias relaciones importantes entre la transformada de Laplace y la transformada de Fourier para señales continuas. En forma similar, pero no idéntica, hay un gran número de relaciones importantes entre la transformada z y la transformada de Fourier de tiempo discreto. Para explorar estas relaciones, expresemos la variable compleja z en forma polar como Siendo r la magnitud de z y ω su ángulo. En términos de r y ω, la ecuación (10. 3) pasa a ser o, de manera equivalente,
La Transformada z •
La Transformada z •
La Transformada z .
La Transformada z .
La Transformada z .
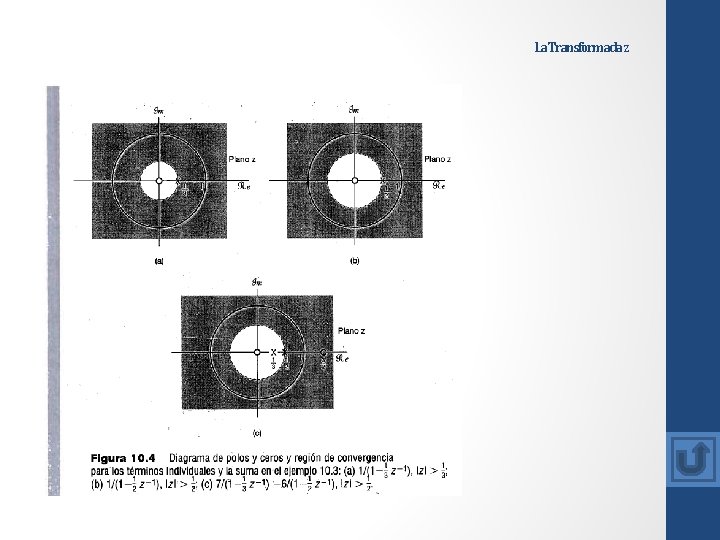
La Transformada z Comparando las ecuaciones (10. 9) y (10. 11), así como las figuras 10. 2 y 10. 3, vemos que la expresión algebraica de X(z) y el diagrama de polos y ceros correspondiente son idénticos en los ejemplos 10. 1 y 10. 2, y la transformada Z difiere sólo en sus regiones de convergencia. Por lo tanto, al igual que con la transformada de Laplace, la especificación de la transformada z requiere tanto de la expresión algebraica como de la región de convergencia. Asimismo, en ambos ejemplos las secuencias fueron exponenciales y las transformadas z resultantes fueron racionales. De hecho, como sugiere el próximo ejemplo, X(z) será racional siempre que x[n] sea una combinación lineal de exponenciales reales o complejas:
La Transformada z .
La Transformada z .
La Transformada z .
La Transformada z •
La Transformada z •
La Transformada z
La Transformada z
La Transformada z
La Transformada z
La Transformada z
La Transformada z
La Transformada z
La Transformada z
La Transformada z
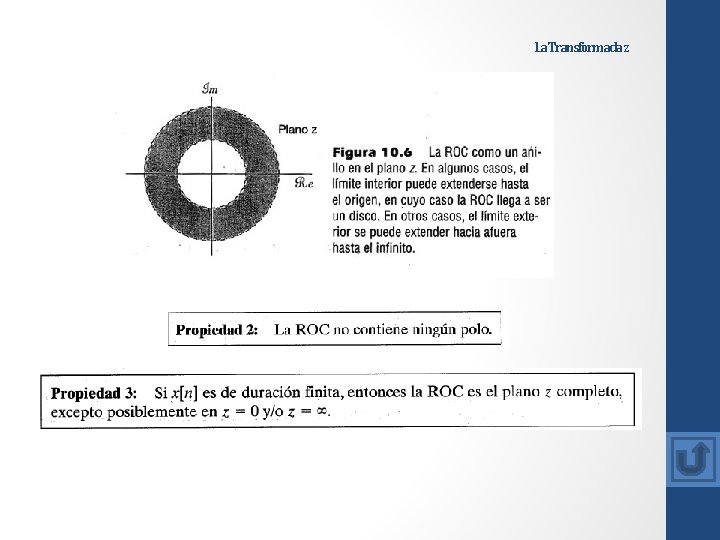
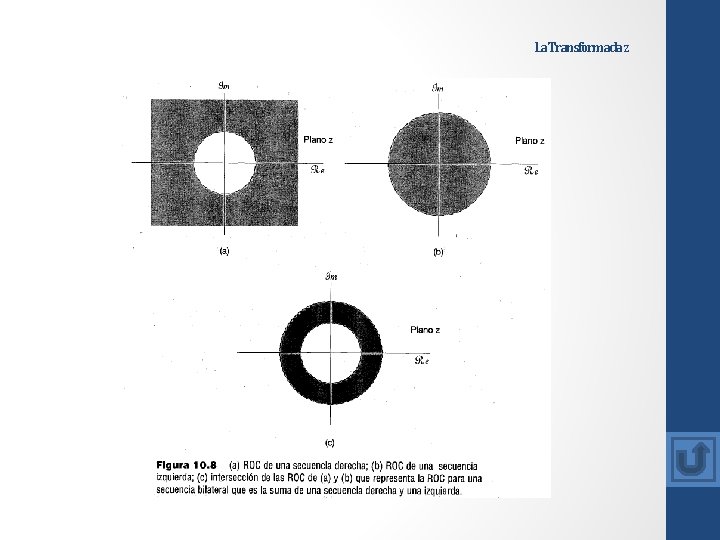
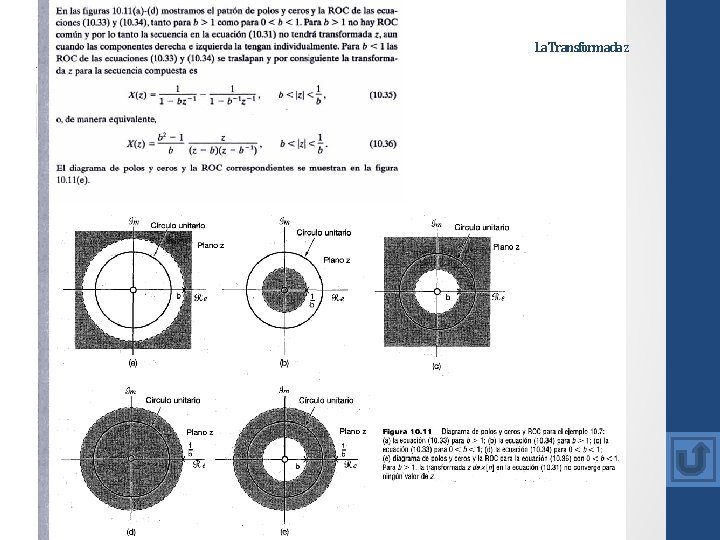
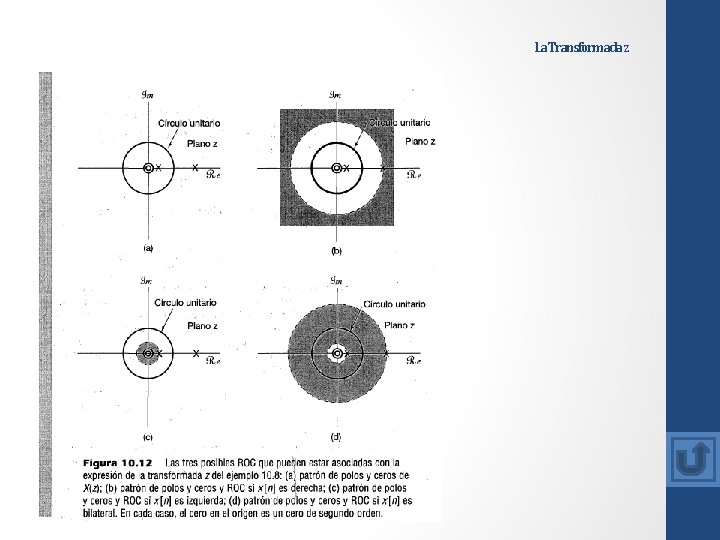
La Transformada z De este modo, para secuencias izquierdas, los polos de X(z) diferentes de cualquiera que esté en z = 0 están mas alejados del origen que lo esta algún punto en la ROC. Para un determinado patrón de polos y ceros o, de forma equivalente, una determinada expresión algebraica racional X(z), hay un numero limitado de ROC diferentes que son congruentes con las propiedades anteriores. Para ilustrar como las diferentes ROC pueden asociarse con el mismo patrón de polos y ceros, presentamos el siguiente ejemplo.
La Transformada z
La Transformada z •
La Transformada z •
La Transformada z Al igual que con la transformada de Laplace inversa, la evaluación formal de la ecuación (10. 41) de la transformada inversa requiere que se utilice la integración de contorno en el plano complejo. Sin embargo, existen diversos procedimientos alternativos para obtener una secuencia a partir de su transformada z. Al igual que con las transformadas de Laplace, un procedimiento particularmente útil para transformadas z racionales consiste en expandir la expresión algebraica en una expansión por fracciones parciales y reconocer las secuencias asociadas con cada uno de los términos individuales. En los siguientes ejemplos ilustraremos dicho procedimiento.
La Transformada z
La Transformada z
La Transformada z Los ejemplos anteriores ilustran el procedimiento básico involucrado en la utilización de la expansión por fracciones parciales para determinar la transformada z inversa. Como sucede con el método correspondiente para la transformada de Laplace, el procedimiento se basa en expresar la transformada z como una combinación lineal de términos más simples. La transformada inversa de cada término se obtiene por inspección. En particular, suponga que la expansión en fracciones parciales de X(z) tiene la forma
La Transformada z •
La Transformada z
La Transformada z
La Transformada z El método de expansión en serie de potencias para obtener la transformada z inversa es en particular útil para transformadas z no racionales, lo cual demostraremos con un ejemplo adicional.
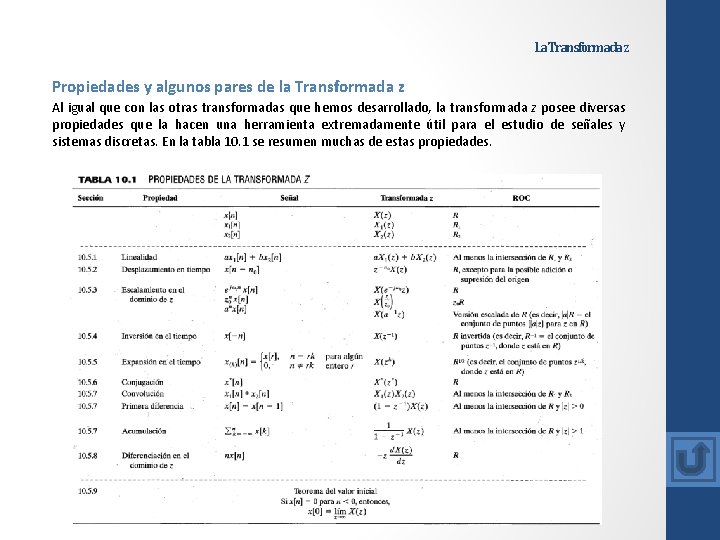
La Transformada z Propiedades y algunos pares de la Transformada z Al igual que con las otras transformadas que hemos desarrollado, la transformada z posee diversas propiedades que la hacen una herramienta extremadamente útil para el estudio de señales y sistemas discretas. En la tabla 10. 1 se resumen muchas de estas propiedades.
La Transformada z Las deducciones son análogas a las deducciones que se hicieron para las propiedades de las otras transformadas, por lo que su estudio y análisis se dejan al estudiante. Estas deducciones se pueden encontrar en el libro de texto. En la tabla 10. 2 se muestran algunos pares relevantes de la transformada a.
La Transformada z
La Transformada z
La Transformada z
La Transformada z
La Transformada z
La Transformada z •
La Transformada z • Causalidad
La Transformada z
La Transformada z • Estabilidad
La Transformada z
La Transformada z
La Transformada z Sistemas LTI caracterizados por ecuaciones de diferencias lineales con coeficientes constantes Para los sistemas caracterizados por ecuaciones de diferencias lineales con coeficientes constantes, las propiedades de la transformada z proporcionan un procedimiento particularmente conveniente para obtener la función del sistema, la respuesta en frecuencia o la respuesta en el dominio del tiempo del sistema. Ilustraremos esto con un ejemplo.
La Transformada z
La Transformada z Para el caso mas general de una ecuaci 6 n de diferencias de orden N, procedemos de forma similar al ejemplo 10. 25, aplicando la transformada z a ambos miembros de la ecuación y usando las propiedades de linealidad y desplazamiento en tiempo. En particular, considere un sistema LTI para el cual la entrada y la salida satisfacen una ecuación de diferencias lineal con coeficientes constantes de la forma Entonces tomamos las transformadas z en ambos miembros de la ecuación (10. 105) y utilizamos las propiedades de linealidad y desplazamiento en el tiempo para obtener o tal que
La Transformada z
La Transformada z
La Transformada z
La Transformada z
La Transformada z
Definicin de cultura
Definicin de estado
Definicin de amor
Definicin
Teoria semitica
Definici9
Definicin de derecho
Monemas esquema
Aprendida
Imagenes
Suponga que se tiene que medir la longitud de un puente
Sexo definicin
Transformada de hough
Transformada de laplace
Paisagem transformada pela natureza
Transformada de fourier escalon unitario
Fwfef
Ledeburita transformada
Sistema de fourier
Discreta
Transformada de fourier
Atividade sobre ambiente natural e modificado
Matriz transformada
Funcion rampa
Frações parciais laplace
Transformada de fourier discreta
Transformada de laplace exemplos
Transformada z
Imagem
Transformada inversa de laplace
Dtft
Tabla transformada z
Transformada de laplace exemplos
Transformada de laplace exemplos
Tabela de transformada de fourier
Ledeburita transformada
M.i. ricardo garibay jimenez
Transformada de hough
