Anlisis de nodos y mallas Circuitos elctricos 1









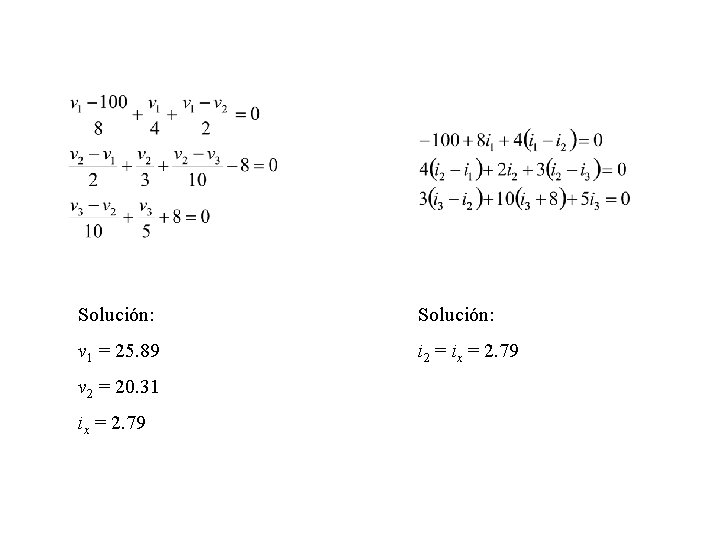
- Slides: 25

Análisis de nodos y mallas Circuitos eléctricos 1

Análisis de nodos En el análisis nodal se aplica la ley de Kirchhoff de corrientes para determinar los voltajes presentes en los nodos. • Es conveniente dibujar la red utilizando valores de conductancias y colapsando los nodos a un solo punto. • Defina un nodo de referencia • Etiquete los nodos restantes de 1 en adelante. • Defina los voltajes de cada nodo (excepto el de referencia) • Escriba LKC para cada nodo • Resuelva el sistema de ecuaciones resultante

Circuitos con fuentes independientes de corriente Consideremos el circuito de la figura a. La figura 1 b es el mismo circuito en donde se hace resaltar la existencia de tres nodos. Dado que los voltajes se definen en pares de nodos, debemos elegir un nodo como referencia para medir dichos voltajes. En la figura c se muestra el mismo circuito con la referencia tomada como el nodo inferior. La figura d muestra la misma red en la que se han eliminado los signos de referencia del voltaje por resultar redundantes.

Aplicando la ley de Kirchhoff de corrientes a cada nodo obtenemos para el nodo 1. 0. 5 v 1 + 0. 2(v 1 - v 2) = 3 o 0. 7 v 1 - 0. 2 v 2 = 3 y para el nodo 2. v 2 + 0. 2(v 2 - v 1) = 2 o - 0. 2 v 1 + 1. 2 v 2 = 2 La solución de este sistema de ecuaciones es: v 1 = 5 V v 2 = 2. 5 V La tensión del nodo 1 respecto al dos será: (v 1 – v 2) = 2. 5 V. con estos valores se puede determinar la potencia disipada por cualquiera de los elementos del circuito. Para circuitos que solo contienen fuentes independientes de corriente se obtiene una matriz de sistema simétrica, llamada matriz de conductancia.

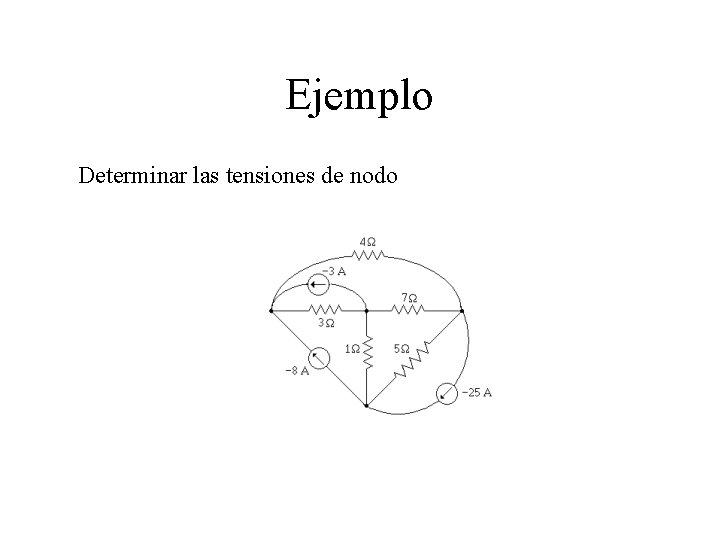
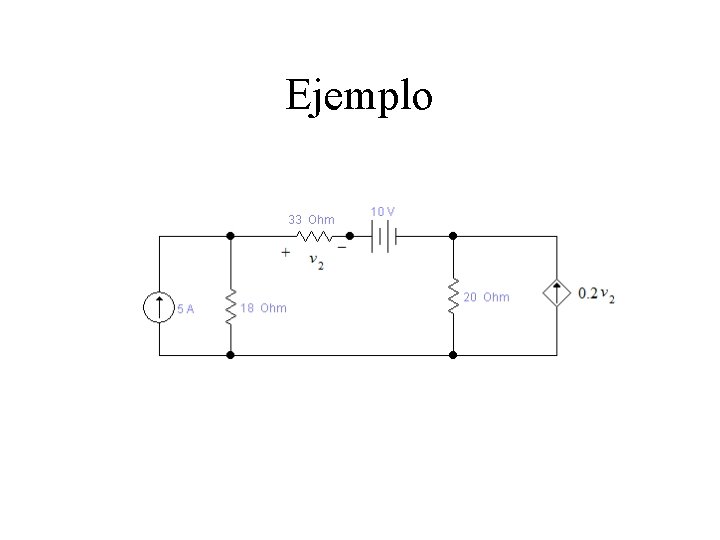
Ejemplo Determinar las tensiones de nodo

Matriz de conductancias La matriz de conductancias es la matriz de coeficientes de del sistema de ecuaciones de nodos. Para redes con solo resistencias y fuentes de corriente independientes la matriz de conductancias es una matriz simétrica. Los elementos de la diagonal, gii, son iguales a la suma de las conductancias del nodo i y los elementos gij , con i <> j, son iguales al negativo de la suma de las conductancias que unen al nodo i y al nodo j. El vector de términos independientes esta formado por la suma de las corrientes que llegan a cada nodo a partir de las fuentes de corriente.

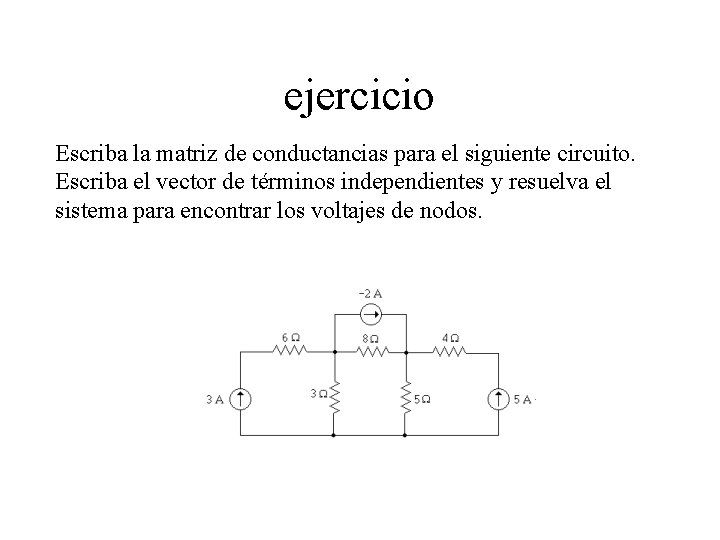
ejercicio Escriba la matriz de conductancias para el siguiente circuito. Escriba el vector de términos independientes y resuelva el sistema para encontrar los voltajes de nodos.

Tarea # 11 Escriba las ecuaciones de nodo utilizando la definición de la matriz de conductancias y resuelva el sistema resultante para calcular los voltajes de nodo de la siguiente red.

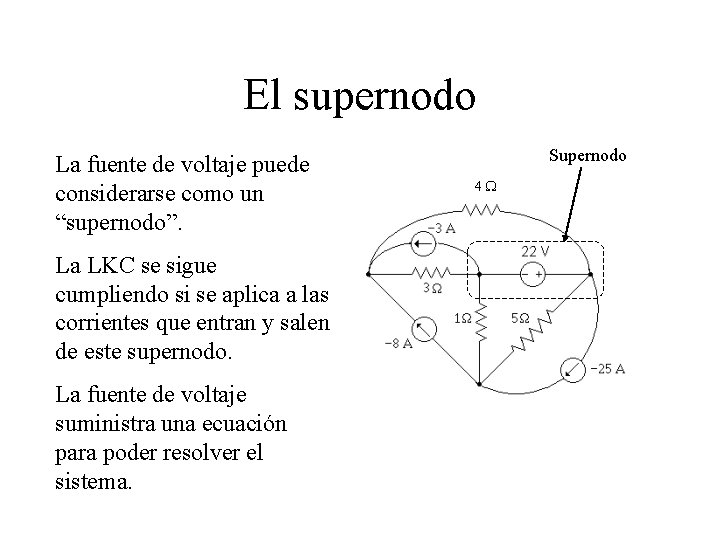
El supernodo La fuente de voltaje puede considerarse como un “supernodo”. La LKC se sigue cumpliendo si se aplica a las corrientes que entran y salen de este supernodo. La fuente de voltaje suministra una ecuación para poder resolver el sistema. Supernodo 4 W

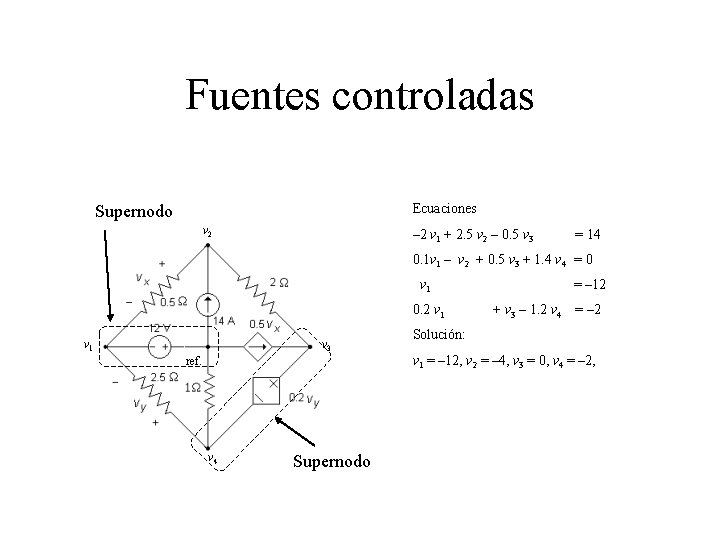
Fuentes controladas Ecuaciones Supernodo v 2 – 2 v 1 + 2. 5 v 2 – 0. 5 v 3 = 14 0. 1 v 1 – v 2 + 0. 5 v 3 + 1. 4 v 4 = 0 v 1 0. 2 v 1 v 3 ref. v 4 Supernodo = – 12 + v 3 – 1. 2 v 4 = – 2 Solución: v 1 = – 12, v 2 = – 4, v 3 = 0, v 4 = – 2,

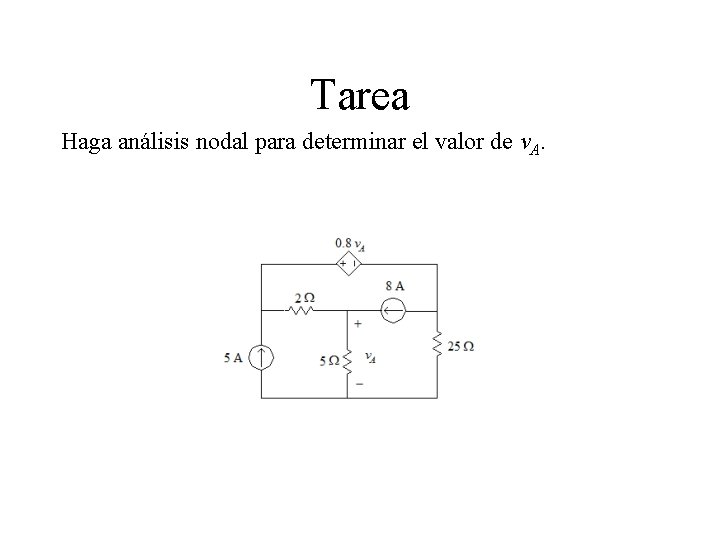
Tarea Haga análisis nodal para determinar el valor de v. A.

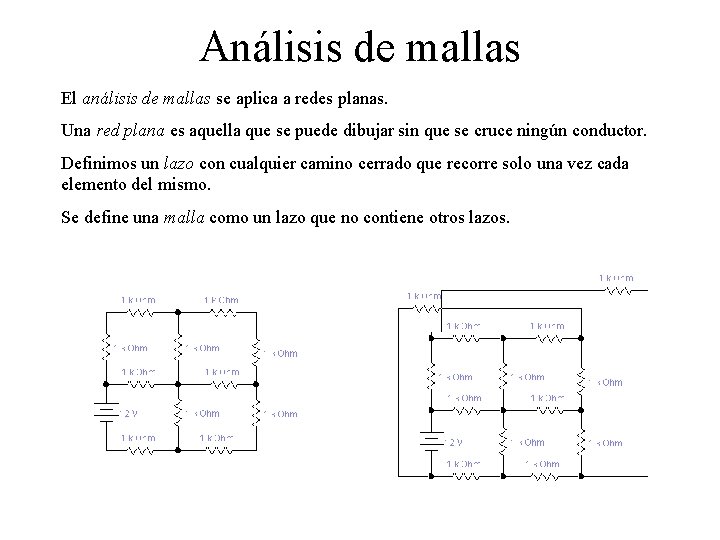
Análisis de mallas El análisis de mallas se aplica a redes planas. Una red plana es aquella que se puede dibujar sin que se cruce ningún conductor. Definimos un lazo con cualquier camino cerrado que recorre solo una vez cada elemento del mismo. Se define una malla como un lazo que no contiene otros lazos.

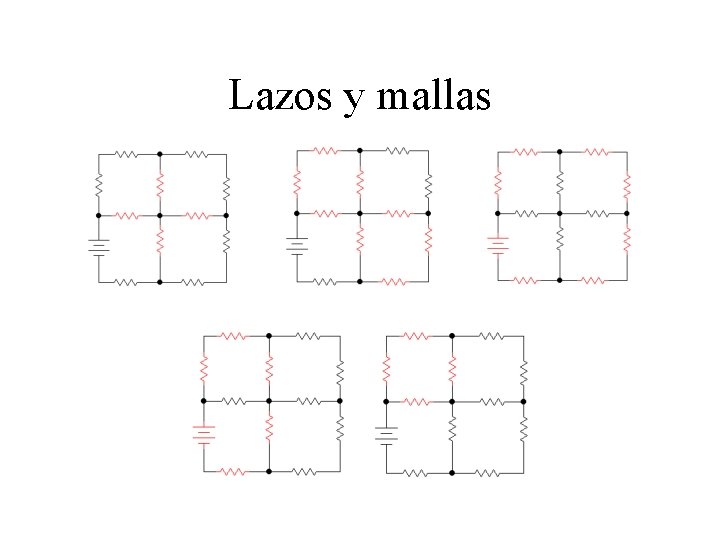
Lazos y mallas

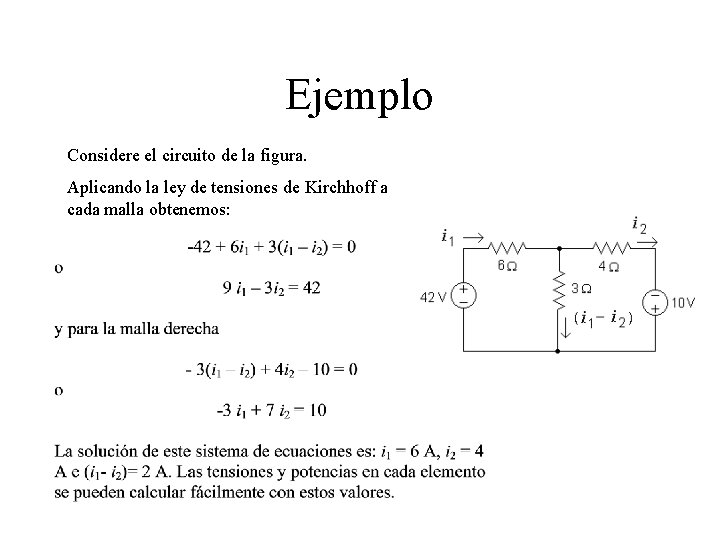
Ejemplo Considere el circuito de la figura. Aplicando la ley de tensiones de Kirchhoff a cada malla obtenemos:

Corriente de malla Definimos corriente de malla como la corriente que circula alrededor del perímetro de una malla. En la figura se muestran las corrientes de malla de la red anterior. La ecuación de malla para la malla 1 es: 6 i 1 + 3(i 1 – i 2) = 42 La ecuación de malla para la malla 2 es: 3(i 2 – i 1) + 4 i 2 = 10 9 i 1 – 3 i 2 = 42 – 3 i 1 + 7 i 2 = 10 La solución es la misma que la anterior.

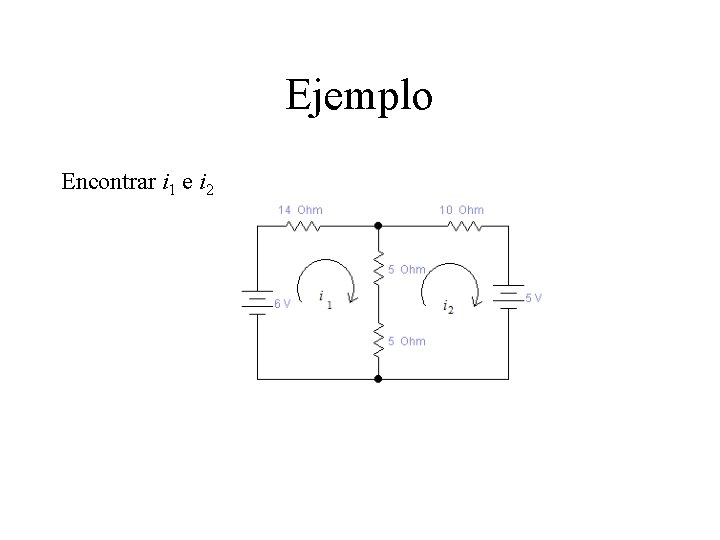
Ejemplo Encontrar i 1 e i 2

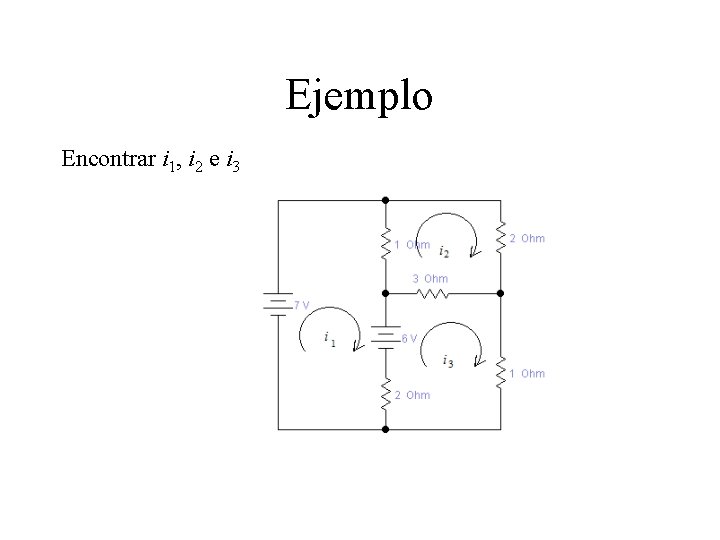
Ejemplo Encontrar i 1, i 2 e i 3

Tarea Encontrar i 1 e i 2

Supermallas La fuente de corriente se puede manejar mediante una supermalla. Las ecuaciones para la red de la derecha son: Para la supermalla: – 7 + 1(i 1 – i 2) + 3(i 3 – i 2) + i 3 = 0 i 1 – 4 i 2 + 3 i 3 = 7 para la malla 2: 1(i 2 – i 1) + 3(i 2 – i 3) + 2 i 2 = 0 – i 1 + 6 i 2 – 3 i 3 = 0 Ecuación de la fuente de corriente: i 1 – i 3 = 7 Solución: i 1 = 9 A, i 2 = 2. 5 A, i 3 = 2 A. i 1 i 2 i 1 i 3

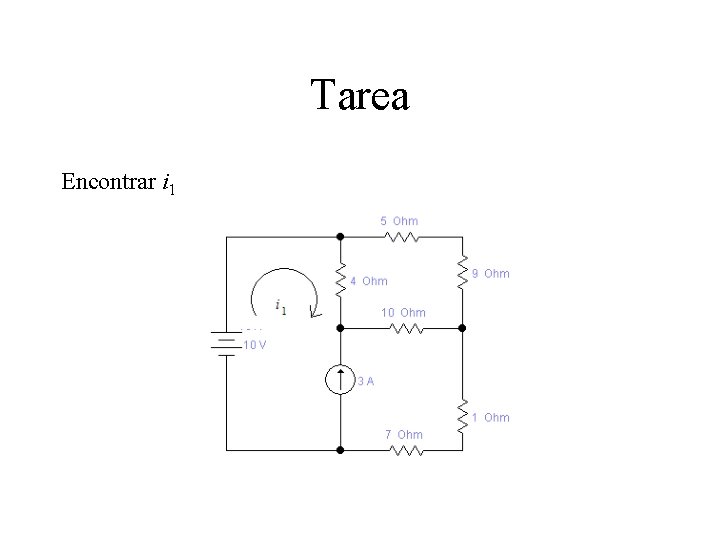
Tarea Encontrar i 1

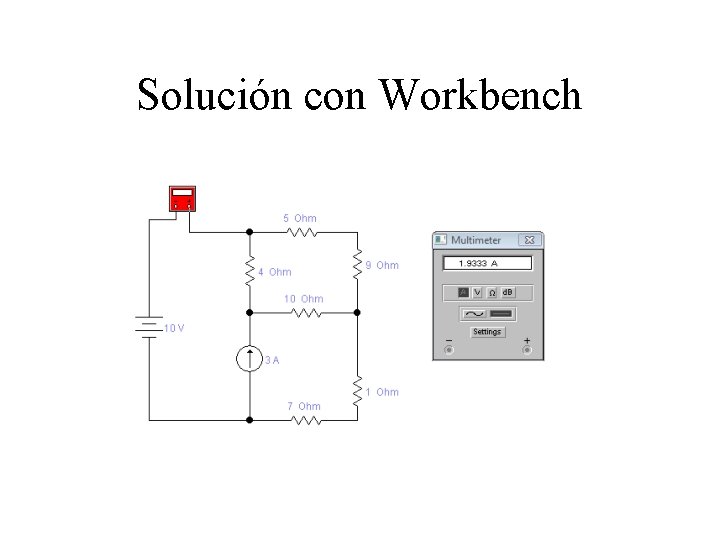
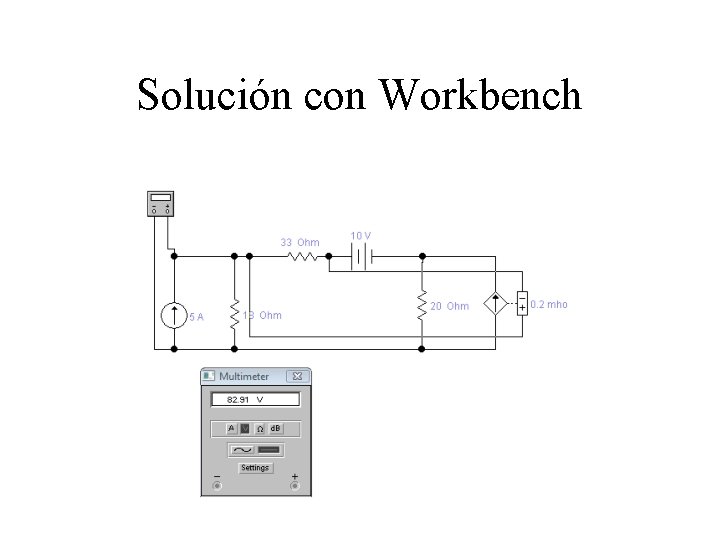
Solución con Workbench

Ejemplo

Solución con Workbench

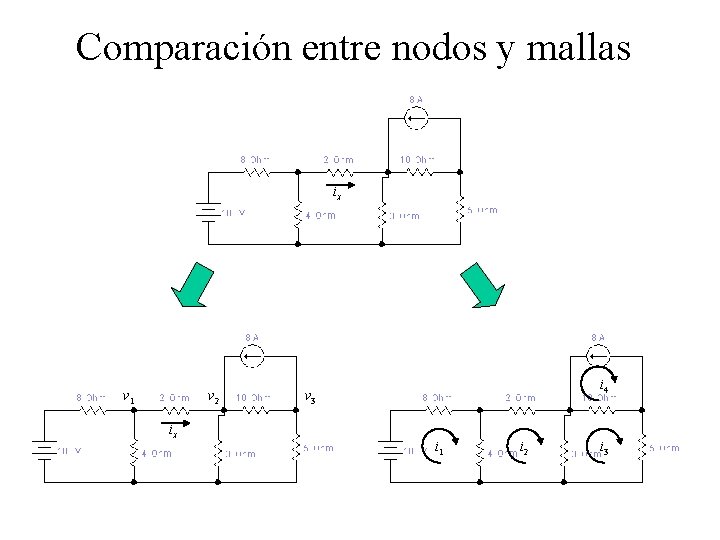
Comparación entre nodos y mallas ix v 1 v 2 ix i 4 v 3 i 1 i 2 i 3
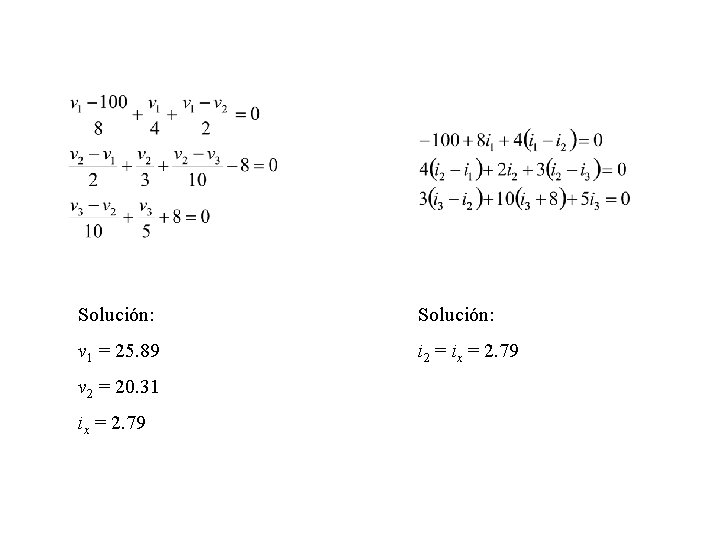
Solución: v 1 = 25. 89 i 2 = ix = 2. 79 v 2 = 20. 31 ix = 2. 79
 Concepto de supernodo
Concepto de supernodo Ramas
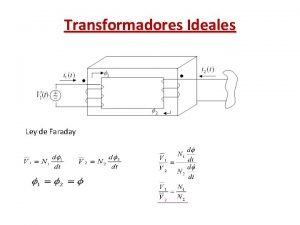
Ramas Transformador de faraday
Transformador de faraday Metodo de mallas circuitos
Metodo de mallas circuitos Calculadora de circuitos por nodos
Calculadora de circuitos por nodos Materiales elctricos
Materiales elctricos Foda del producto
Foda del producto Anlisis foda
Anlisis foda Anlisis financiero
Anlisis financiero Master memfi
Master memfi Estrategia fa (maxi-mini)
Estrategia fa (maxi-mini) Ambientales
Ambientales Metodo mallas
Metodo mallas Mállás
Mállás Molienda y tamizado
Molienda y tamizado Metodo de mallas corriente alterna
Metodo de mallas corriente alterna Invertir un arbol binario
Invertir un arbol binario Que estructura es
Que estructura es Fuerza colineal
Fuerza colineal Nodos regionales de cambio climático
Nodos regionales de cambio climático Reações de apoio
Reações de apoio Telodendrón
Telodendrón Circuitos integrados
Circuitos integrados Circuitos integrados
Circuitos integrados Circuitos acoplados magnéticamente
Circuitos acoplados magnéticamente Circuitos msi
Circuitos msi