FUNCIONES POTENCIALES EXPONENCIALES Y LOGARTMICAS 4 ESO y

FUNCIONES POTENCIALES, EXPONENCIALES Y LOGARÍTMICAS. 4º ESO y 1º Bachillerato

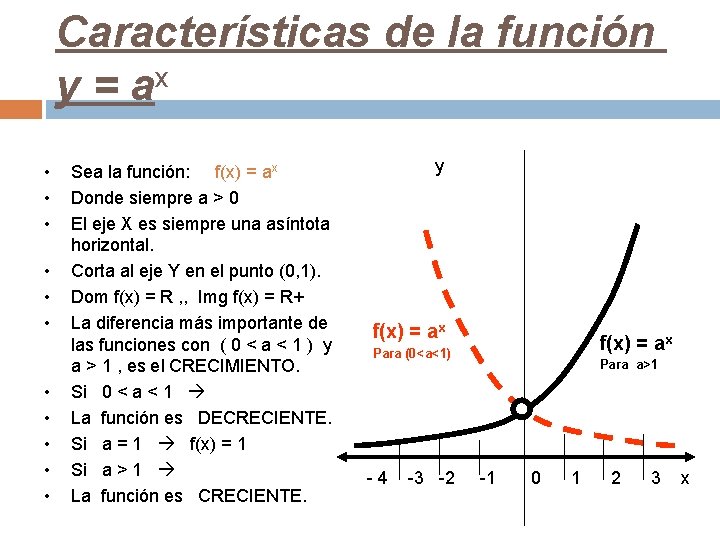
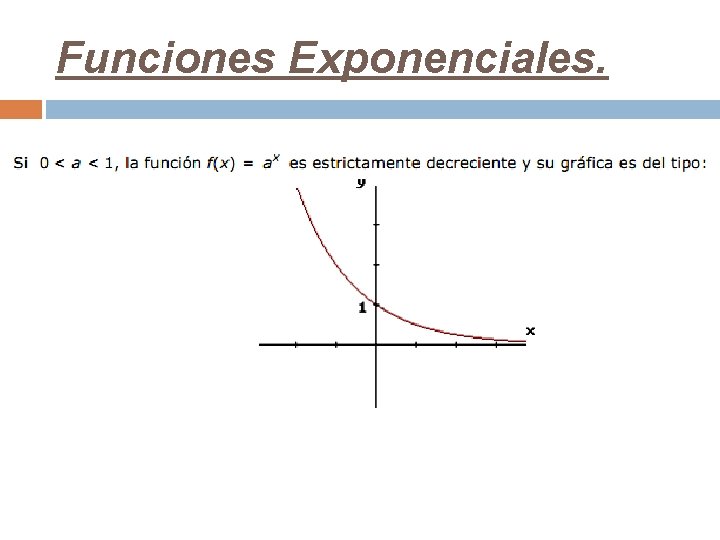
Características de la función y = ax • • • Sea la función: f(x) = ax Donde siempre a > 0 El eje X es siempre una asíntota horizontal. Corta al eje Y en el punto (0, 1). Dom f(x) = R , , Img f(x) = R+ La diferencia más importante de las funciones con ( 0 < a < 1 ) y a > 1 , es el CRECIMIENTO. Si 0 < a < 1 La función es DECRECIENTE. Si a = 1 f(x) = 1 Si a > 1 La función es CRECIENTE. y f(x) = ax Para (0<a<1) f(x) = ax Para a>1 - 4 -3 -2 -1 0 1 2 3 x

La función exponencial y=2 x 2 y la función cuadrática y=x Sea la función exponencial f (x) = 2 x Está representada en color NEGRO La base es un número y el exponente es la variable independiente. Sea la función polinómica f (x) = x 2 Está representada en color ROJO La base es la variable independiente y el exponente es un número. y 9 8 f (x) = x 2 f (x) = 2 x 4 2 1 -3 -2 -1 0 1 2 3

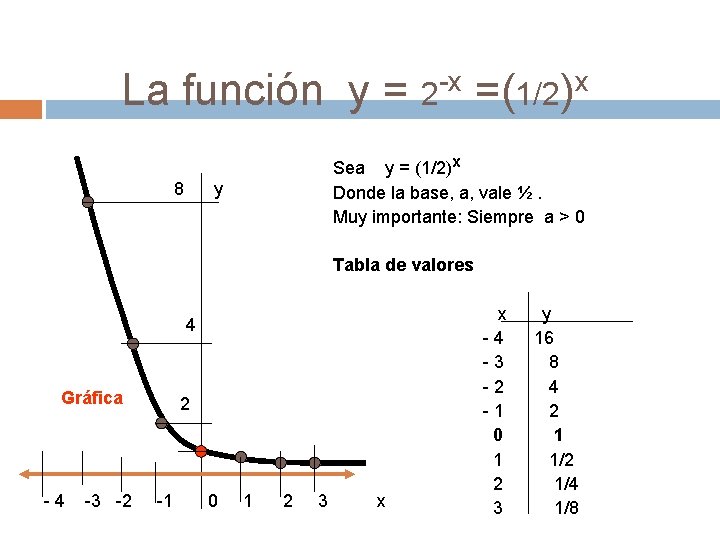
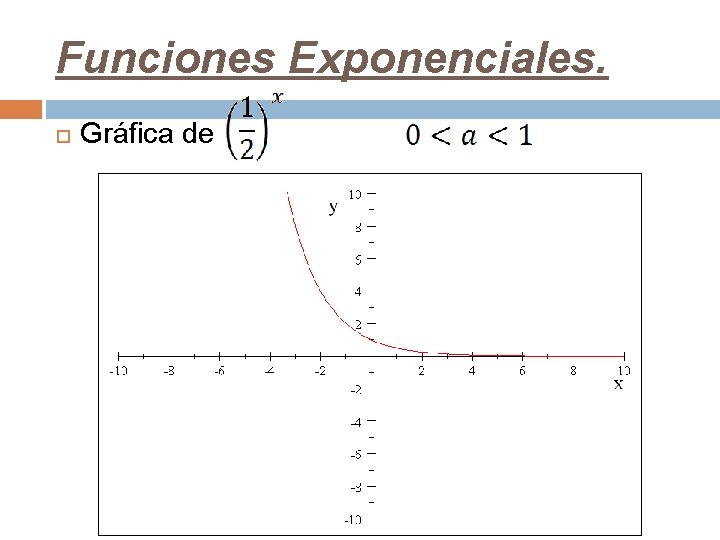
-x x La función y = 2 =(1/2) 8 y Sea y = (1/2)x Donde la base, a, vale ½. Muy importante: Siempre a > 0 Tabla de valores x y - 4 16 - 3 8 - 2 4 Gráfica 2 - 1 2 0 1 1 1/2 2 1/4 - 4 -3 -2 -1 0 1 2 3 x 3 1/8 4

La población mundial Un grupo de expertos en demografía tras estudiar el crecimiento de la población mundial, ha establecido que esta población, y, en función del año correspondiente, x, puede expresarse según la siguiente ecuación: y = 100, 00389 x+2 a) Dibuja la gráfica de esta función. b) ¿En qué año la población alcanzó los millones? . c) ¿Y los 3 millones? d) Del mismo modo calcula en que año alcanzará los 6 millones de habitantes.

Declive de un valor Digamos que comenzaste un pequeño negocio y compraste una camioneta nueva para hacer entregas. La camioneta tuvo un costo de 25. 000 € y de acuerdo a la ley de impuestos, te es permitido depreciar su valor por 15% por año. Esto significa que después de la depreciación del primer año, el valor de la camioneta será de solamente 85% de su costo original, o 21. 250 €. La fórmula: y = 25000. (1 – 0, 15)x y = 25000. (0, 85)x predecirá el valor de la camioneta después de x años de depreciación a 15% por año.

Tenemos 1. ¿Disminuye el valor de la camioneta la misma cantidad cada año? El primer año, por ser mayor el valor inicial. 3. ¿Cuándo es menor la caída en valor? No, pues aunque disminuye siempre el 15%, lo hace sobre cantidades diferentes. 2. ¿Cuándo es mayor la caída en valor? Nunca, pues por muchos años que pasen siempre quedará algún valor. 4. ¿No tendrá ningún valor la camioneta en algún momento, de acuerdo a este modelo? . El resultado nunca puede ser negativo. 6. ¿Cuánto tiempo deberá transcurrir para que su valor fiscal sea de 5. 000 €, de acuerdo a este modelo? El resultado nunca puede ser 0. 5. ¿Tendrá la camioneta en algún momento un valor negativo, de acuerdo a este modelo? y = 25000. (0, 85)x 5000 = 25000. (0, 85)x 5000/25000 = 0, 85 x 0, 2 = 0, 85 x ln 0, 2 = x. ln 0, 85 ln 0, 2 - 1, 609437 x = ---------------- = 10 años aproximadamente ln 0, 85 - 0, 162519

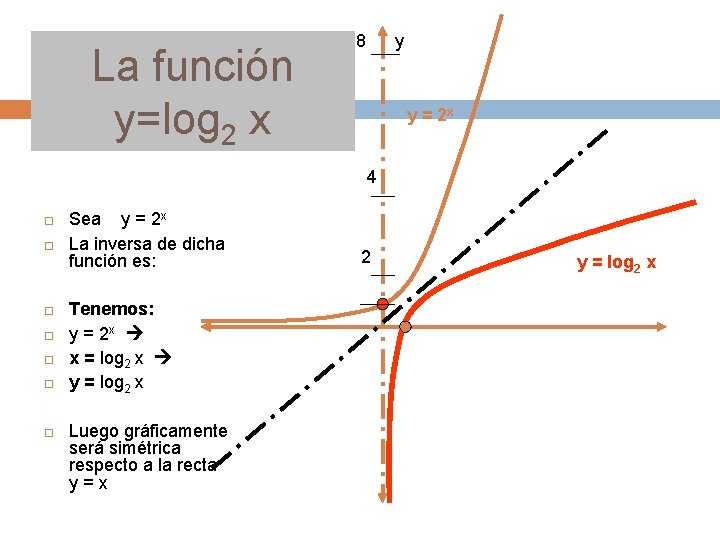
La función y=log 2 x 8 y y = 2 x 4 Sea y = 2 x La inversa de dicha función es: Tenemos: y = 2 x x = log 2 x y = log 2 x Luego gráficamente será simétrica respecto a la recta y = x 2 y = log 2 x

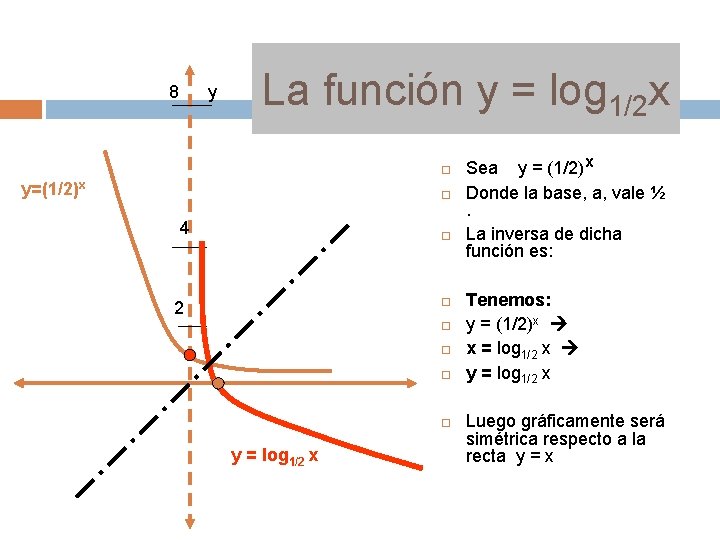
8 y La función y = log 1/2 x y=(1/2)x 4 2 y = log 1/2 x Sea y = (1/2)x Donde la base, a, vale ½ . La inversa de dicha función es: Tenemos: y = (1/2)x x = log 1/2 x y = log 1/2 x Luego gráficamente será simétrica respecto a la recta y = x

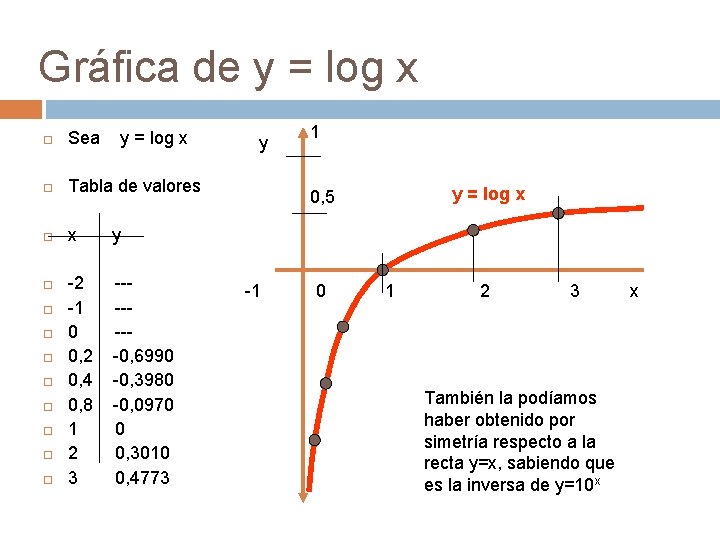
Gráfica de y = log x Sea y = log x Tabla de valores x y y 1 0, 5 y = log x -2 -- -1 0 1 2 3 x -1 --0, 2 -0, 6990 0, 4 -0, 3980 También la podíamos 0, 8 -0, 0970 haber obtenido por 1 0 simetría respecto a la 2 0, 3010 recta y=x, sabiendo que 3 0, 4773 es la inversa de y=10 x

Gráfica de y = ln x Sea y = ln x Tabla de valores x y y 1 y = ln x 0, 5 -2 -- -1 0 1 2 3 x -1 --0, 2 -1, 6094 0, 4 -0, 9163 0, 8 -0, 2231 1 0 2 0, 6931 3 0, 9861

Comparativa y propiedades Sea y = log x e y = ln x En general, si y = loga x , a > 1 , se cumple: El domino es Dom f(x) = R+ El recorrido es Img f(x) = R Es siempre creciente en R+ Sea cual sea la base, “a” corta al eje de abscisas en el punto P(1, 0) El eje de ordenadas es una ASÍNTOTA de la función, pues ésta tiende a converger con el eje. y y = ln x y = log x 0 1 2 3 x Aunque para valores grandes de x, el valor de y casi es cte. , éste sigue creciendo hasta el infinito, por ello la Img f(x) es R.

Repaso. Algunas funciones Potenciales Se llama función potencia a cualquier expresión que se pueda escribir de la forma: Con a cualquier número real. Son funciones potencias: x 2, x-1 (1/x), x 1/2 (Raiz de x)

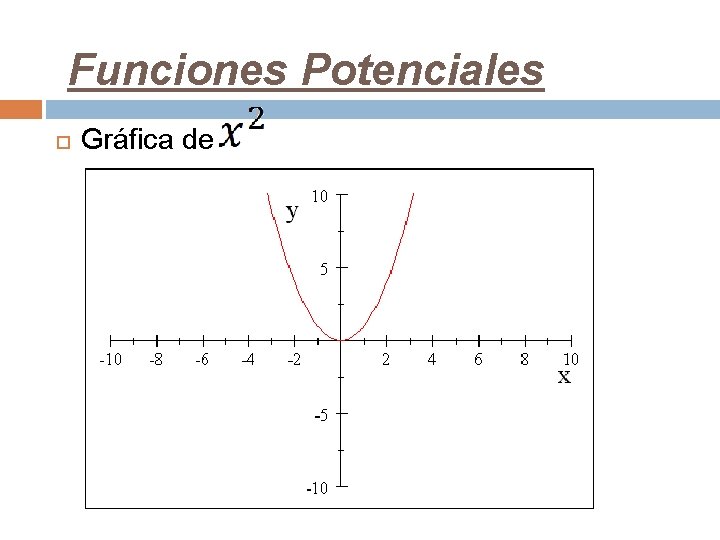
Funciones Potenciales Gráfica de

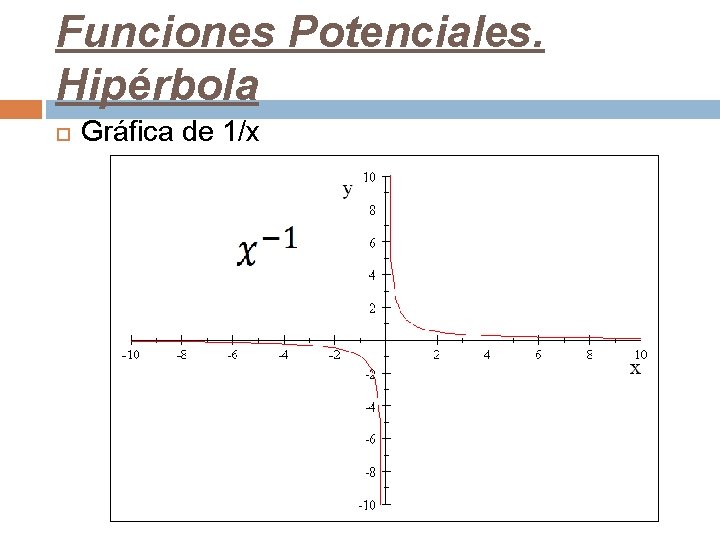
Funciones Potenciales. Hipérbola Gráfica de 1/x

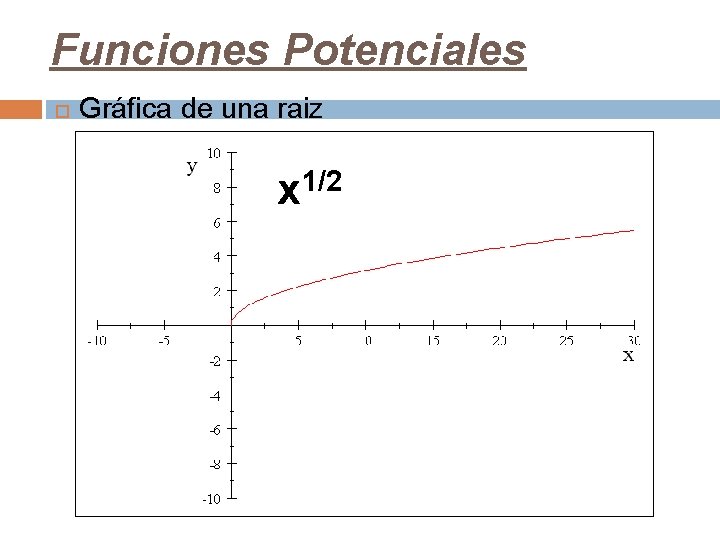
Funciones Potenciales Gráfica de una raiz x 1/2

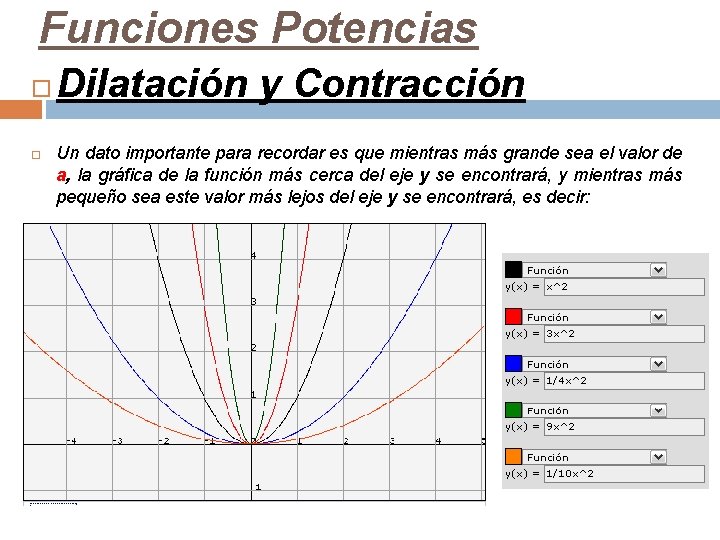
Funciones Potencias Dilatación y Contracción Un dato importante para recordar es que mientras más grande sea el valor de a, la gráfica de la función más cerca del eje y se encontrará, y mientras más pequeño sea este valor más lejos del eje y se encontrará, es decir:

Funciones Exponenciales. Se llama función exponencial de base a, a>0, a la función de la forma: Ejemplos:

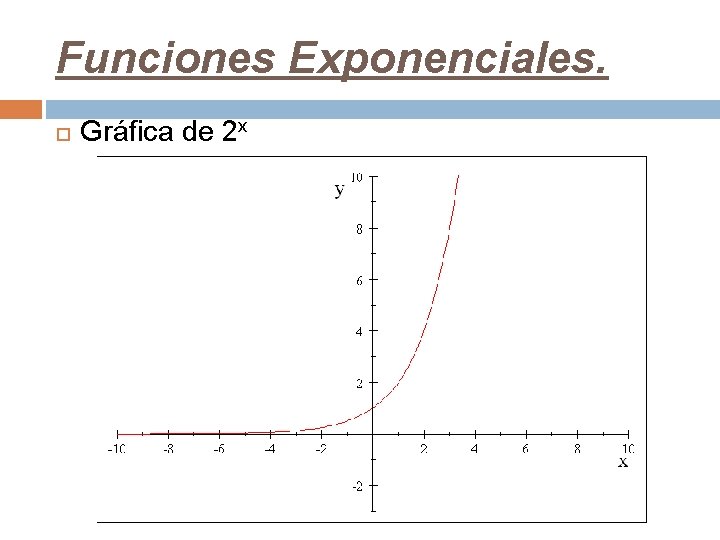
Funciones Exponenciales. Gráfica de 2 x

Funciones Exponenciales.

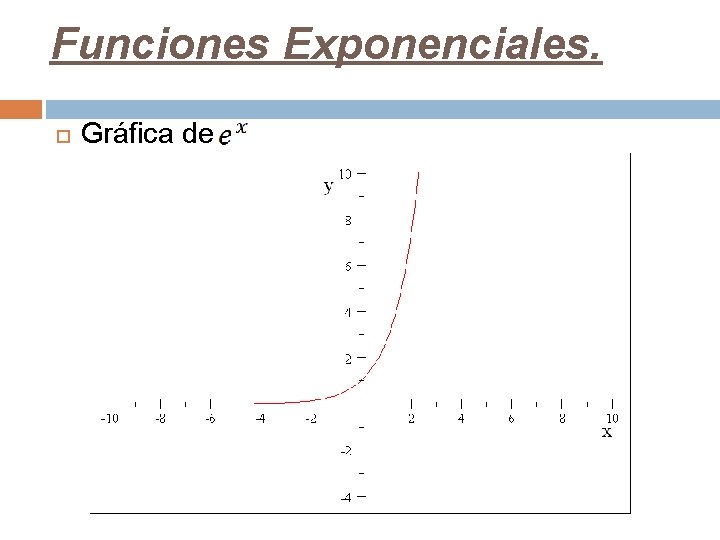
Funciones Exponenciales. Gráfica de

Funciones Exponenciales.

Funciones Exponenciales. Gráfica de

Funciones Exponenciales. Gráfica de 8 x

Ecuaciones Exponenciales. Una ecuación exponencial es aquella ecuación en la que la incógnita aparece en el exponente. Para resolver una ecuación exponencial vamos a tener en cuenta:

Ecuaciones Exponenciales. Propiedades a considerar.

Ecuaciones Exponenciales. Resuelva.

LOGARITMOS Definición: Logaritmo de un número positivo N en una base b, positiva y diferente de 1, es el exponente x al cual debe elevarse la base para obtener el número N. Los logaritmos se pueden presentar de dos formas: Exponencial y Logarítmica,

Propiedades de los Logaritmos. El logaritmo de la misma base siempre es 1.

Propiedades de los Logaritmos. El logaritmo de 1, en cualquier base , es igual a cero.

Propiedades de los Logaritmos. El logaritmo de un producto es igual a la suma de los logaritmos de los factores.

Propiedades de los Logaritmos. El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor.

Propiedades de los Logaritmos. El logaritmo de una potencia es igual al exponente por el logaritmo de la base.

Propiedades de los Logaritmos. El logaritmo de una raíz es igual al logaritmo del radicando dividido entre el índice (exponente fraccionario).