UNIDAD 9 Movimiento oscilatorio 9 1 Oscilaciones oscilaciones















- Slides: 26

UNIDAD 9: Movimiento oscilatorio 9 -1 Oscilaciones, oscilaciones de un resorte 9 -2 Movimiento armónico simple (MAS) 9 -3 Posición, velocidad y aceleración del MAS 9 -4 Energía del MAS 9 -5 Movimiento circular y ecuaciones del MAS 9 -6 Péndulo simple. Péndulo físico 9 -7 Oscilaciones amortiguadas

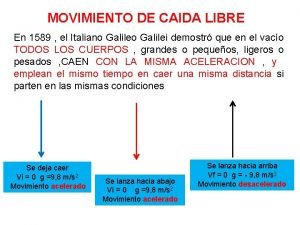
9 -1 Oscilaciones, oscilaciones de un resorte Muchos tipos de movimientos se repiten una y otra vez con el transcurso del tiempo A esta clase de movimiento se lo llama Movimiento Periódico u Oscilatorio y comprenderlo, resulta fundamental para el estudio de ondas, sonido, luz, etc.

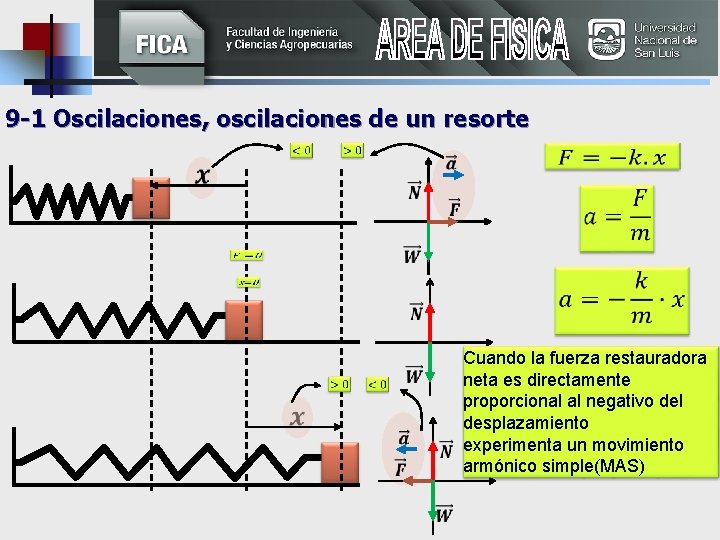
9 -1 Oscilaciones, oscilaciones de un resorte Cuando la fuerza restauradora neta es directamente proporcional al negativo del desplazamiento experimenta un movimiento armónico simple(MAS)

9 -1 Oscilaciones, oscilaciones de un resorte Algunas definiciones importantes 1)Amplitud A: Es el desplazamiento máximo, o distancia más grande desde el punto de equilibrio. 2)Un ciclo: Movimiento completo de ida y vuelta desde algún punto inicial y de regreso a ese mismo punto. 3)Periodo T: Tiempo requerido para efectuar un ciclo completo 4)Frecuencia f: Número de ciclos completos por segundo.

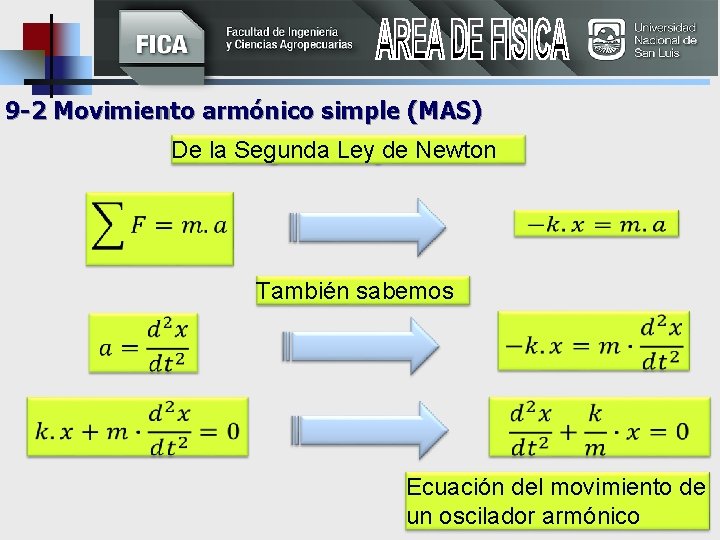
9 -2 Movimiento armónico simple (MAS) De la Segunda Ley de Newton También sabemos Ecuación del movimiento de un oscilador armónico

9 -2 Movimiento armónico simple (MAS)

9 -2 Movimiento armónico simple (MAS) Matemáticamente es una Ecuación diferencial Resolver esto, es encontrar una x(t) que reemplazada en la ecuación la satisfaga Observando, parece una función seno o coseno en función del tiempo con una amplitud A Propongamos como solución de la ecuación: Donde: y es para hacerla mas general

9 -3 Posición, velocidad y aceleración del MAS Para comprobar si es la solución, tenemos que derivar dos veces. Reemplazamos en:

9 -3 Posición, velocidad y aceleración del MAS Sacando factor común, podemos escribir: La solución satisface la ecuación solo cuando: La amplitud A y el ángulo (constante de fase o ángulo de fase inicial) en situaciones físicas reales quedan definidas con las condiciones iniciales para t =0

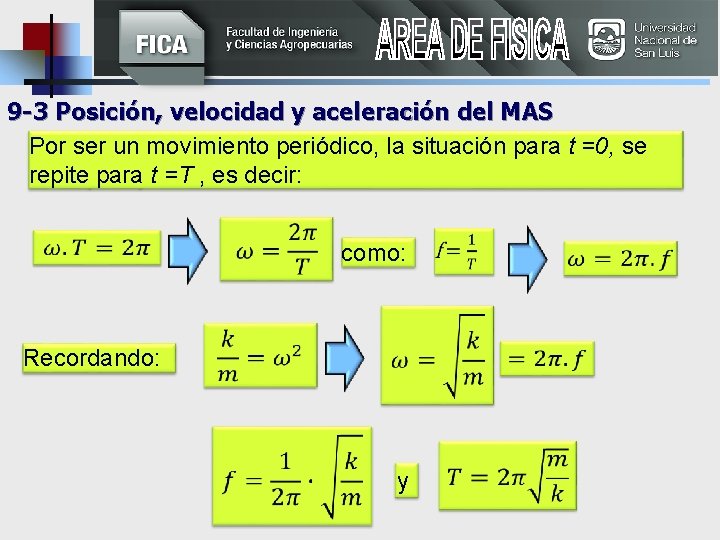
9 -3 Posición, velocidad y aceleración del MAS Por ser un movimiento periódico, la situación para t =0, se repite para t =T , es decir: Recordando: como: y

9 -3 Posición, velocidad y aceleración del MAS la frecuencia y el periodo no dependen de la amplitud cuanto mayor sea la masa, menor será la frecuencia cuanto más rígido sea el resorte, mayor será la frecuencia

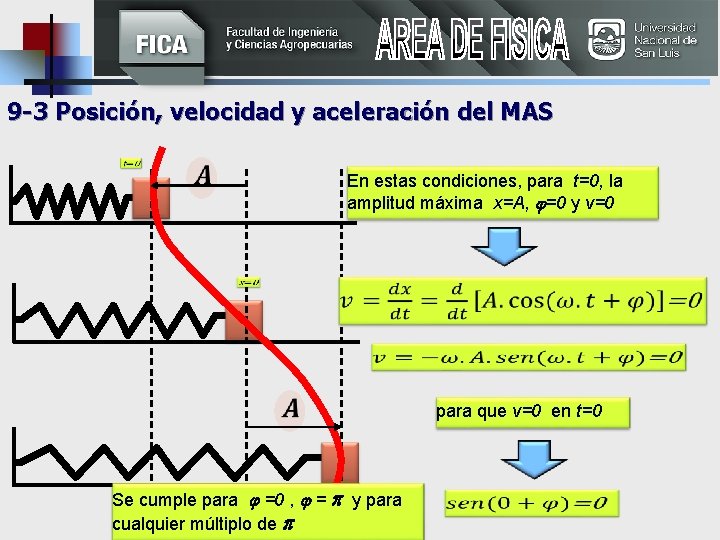
9 -3 Posición, velocidad y aceleración del MAS En estas condiciones, para t=0, la amplitud máxima x=A, =0 y v=0 Se cumple para =0 , = y para cualquier múltiplo de para que v=0 en t=0

9 -3 Posición, velocidad y aceleración del MAS De igual manera, para t=0 =0 , = y para cualquier múltiplo de

9 -3 Posición, velocidad y aceleración del MAS Ejemplo. Un resorte se estira 0. 150 m cuando se cuelga suavemente de él una masa de 0. 300 kg, como en la figura. Luego el resorte se coloca horizontalmente con la masa de 0. 300 kg descansando sobre una mesa sin fricción, como en la figura. La masa se empuja de manera que el resorte se comprime 0. 100 m del punto de equilibrio, y se libera a partir del reposo. Determine: a)la constante de rigidez del resorte k y la frecuencia angular ; b)la amplitud de la oscilación horizontal A; c)la magnitud de la velocidad máxima, vmáx; d)la magnitud de la aceleración máxima de la masa, amáx; e)el periodo T y la frecuencia f; f)el desplazamiento x en función del tiempo; y g)la velocidad en t =0. 150 s. 1 x = -A 2 x=0 x = +A x

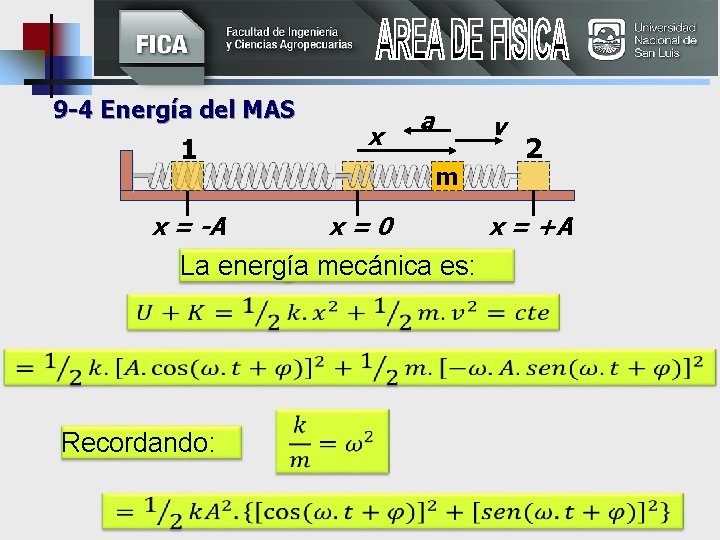
9 -4 Energía del MAS 1 x a v m x = -A x=0 La energía mecánica es: Recordando: 2 x = +A

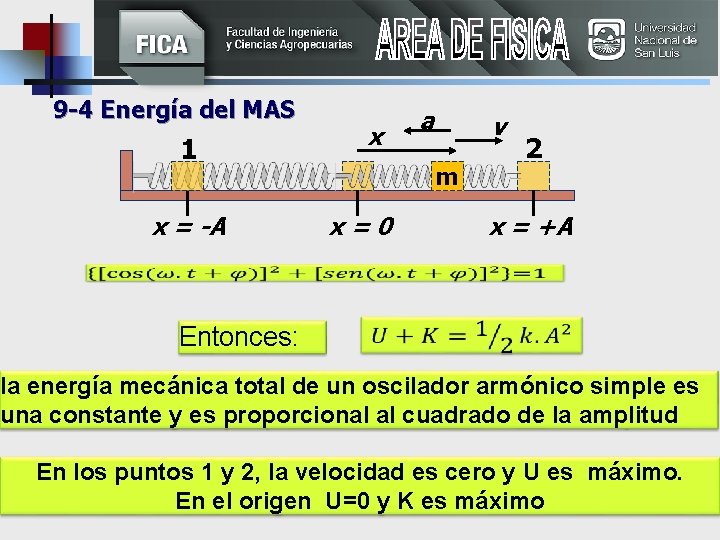
9 -4 Energía del MAS 1 x = -A x a v m x=0 2 x = +A Entonces: la energía mecánica total de un oscilador armónico simple es una constante y es proporcional al cuadrado de la amplitud En los puntos 1 y 2, la velocidad es cero y U es máximo. En el origen U=0 y K es máximo

9 -4 Energía del MAS 1 v x m x = -A x=0 2 x = +A La ecuación de la energía entre el puntos 1 o 2 y cualquier punto intermedio es: Despejando v: Para x=0 ⇾ v=max Velocidad como función de la posición

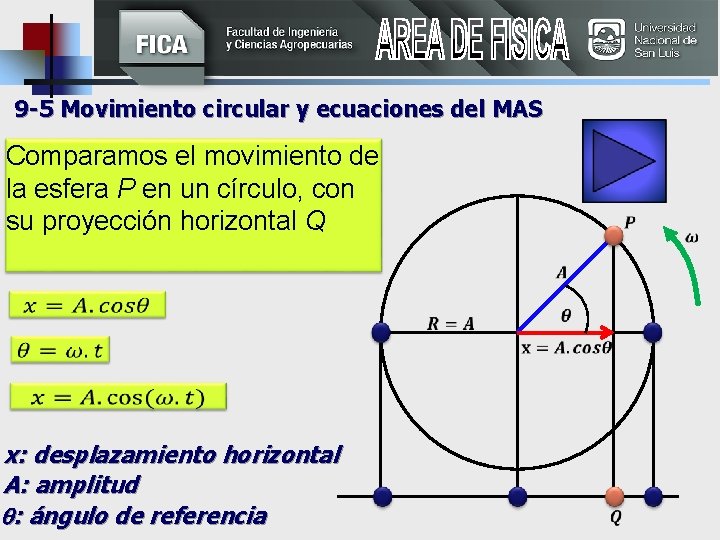
9 -5 Movimiento circular y ecuaciones del MAS Comparamos el movimiento de la esfera P en un círculo, con su proyección horizontal Q x: desplazamiento horizontal A: amplitud : ángulo de referencia

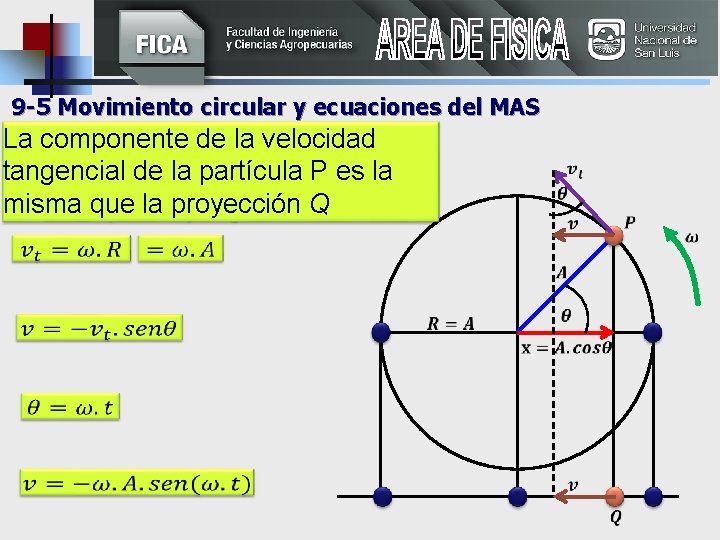
9 -5 Movimiento circular y ecuaciones del MAS La componente de la velocidad tangencial de la partícula P es la misma que la proyección Q

9 -5 Movimiento circular y ecuaciones del MAS La componente de la aceleración centrípeta de la partícula P es la misma que la proyección Q Recordando

9 -5 Movimiento circular y ecuaciones del MAS Recordando las características de la aceleración para un movimiento armónico simple(MAS) La aceleración es directamente proporcional al negativo del desplazamiento, características que tiene un movimiento armónico simple(MAS) Estas ecuaciones son iguales siempre que la velocidad angular se relacione con la masa y la constante de la fuerza del elemento oscilante

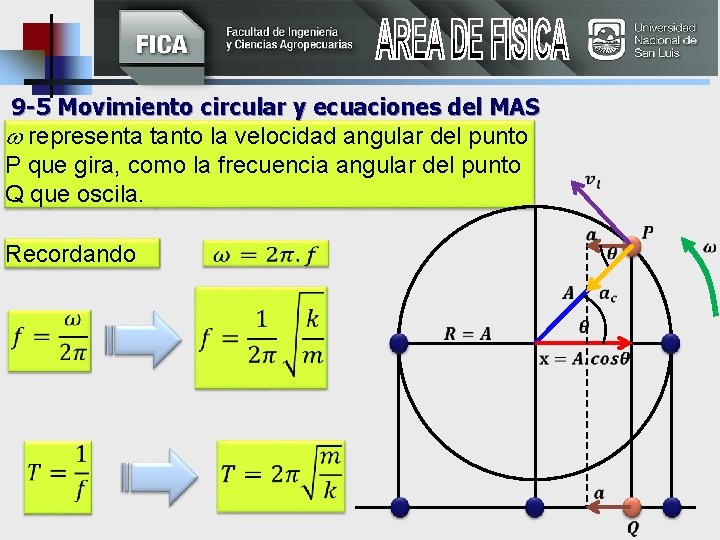
9 -5 Movimiento circular y ecuaciones del MAS representa tanto la velocidad angular del punto P que gira, como la frecuencia angular del punto Q que oscila. Recordando

9 -6 Péndulo simple Para ángulos menores a 15° medidos en radianes Recordando

9 -6 Péndulo simple Ecuación del movimiento de un oscilador armónico

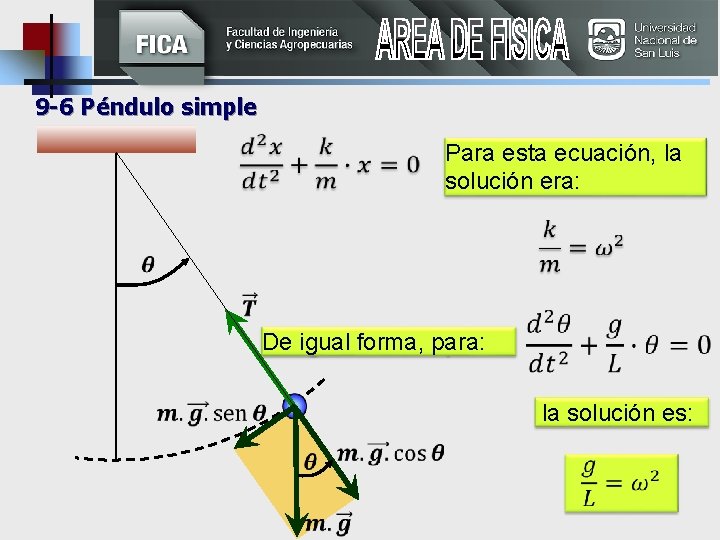
9 -6 Péndulo simple Para esta ecuación, la solución era: De igual forma, para: la solución es:

9 -6 Péndulo simple De manera análoga, la frecuencia y el período serán: la frecuencia y el periodo, igual que en caída libre, no dependen de la masa cuanto mayor sea la longitud del péndulo, menor será la frecuencia cuanto mayor sea g, mayor fuerza de restitución y mayor será la frecuencia
 Clases de movimiento oscilatorio
Clases de movimiento oscilatorio Centena
Centena Ecuacion de la segunda ley de newton
Ecuacion de la segunda ley de newton Potencia electrica
Potencia electrica Oscilaciones
Oscilaciones Jose aguera soriano
Jose aguera soriano Oscilaciones y ondas
Oscilaciones y ondas Dcl
Dcl Movimiento circular uniforme ejemplos
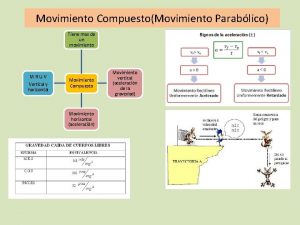
Movimiento circular uniforme ejemplos Movimiento parabolico ppt
Movimiento parabolico ppt Generacin del 27
Generacin del 27 Conclusion de movimiento circular uniforme
Conclusion de movimiento circular uniforme Tipos de comportamiento colectivo
Tipos de comportamiento colectivo Contexto historico social y cultural del realismo
Contexto historico social y cultural del realismo Los 5 pilares del movimiento familiar cristiano
Los 5 pilares del movimiento familiar cristiano Cartucho es verbal o no verbal
Cartucho es verbal o no verbal Boom latinoamericano características
Boom latinoamericano características El ritmo por radiación
El ritmo por radiación Machine
Machine Objetos que se pueden jalar
Objetos que se pueden jalar Movimiento ondulatorio ejemplos
Movimiento ondulatorio ejemplos Tipos de movimiento
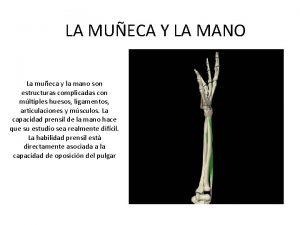
Tipos de movimiento Musculos de la mano
Musculos de la mano Historia del movimiento scout
Historia del movimiento scout Teorema del valor medio
Teorema del valor medio Movimiento medico 1964
Movimiento medico 1964 Xix movimiento literario
Xix movimiento literario