Anlisis Matemtico Integral Definida Ing Antonio Crivillero Arqumedes

Análisis Matemático - Integral Definida - Ing. Antonio Crivillero

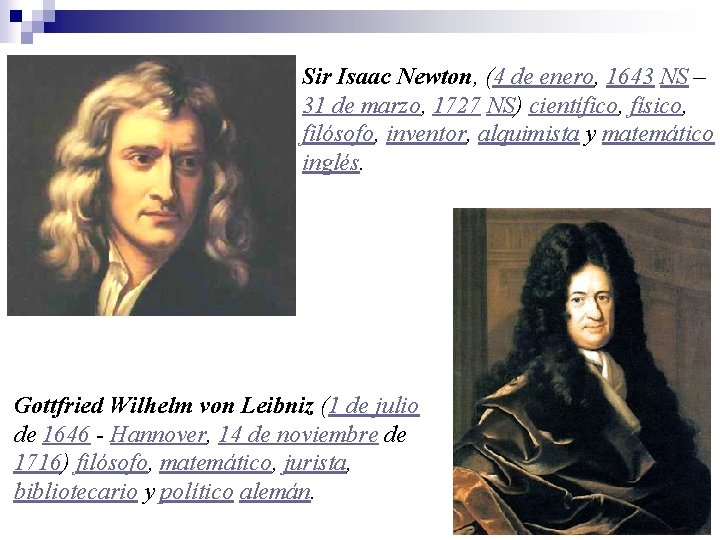
Arquímedes de Siracusa (c. 287 a. C. – c. 212 a. C. ) matemático griego, físico, ingeniero, inventor y astrónomo.

Sir Isaac Newton, (4 de enero, 1643 NS – 31 de marzo, 1727 NS) científico, físico, filósofo, inventor, alquimista y matemático inglés. Gottfried Wilhelm von Leibniz (1 de julio de 1646 - Hannover, 14 de noviembre de 1716) filósofo, matemático, jurista, bibliotecario y político alemán.

Georg Friedrich Bernhard Riemann (17 de septiembre de 1826 - 20 de junio de 1866) matemático alemán que realizó contribuciones muy importantes en análisis y geometría diferencial.

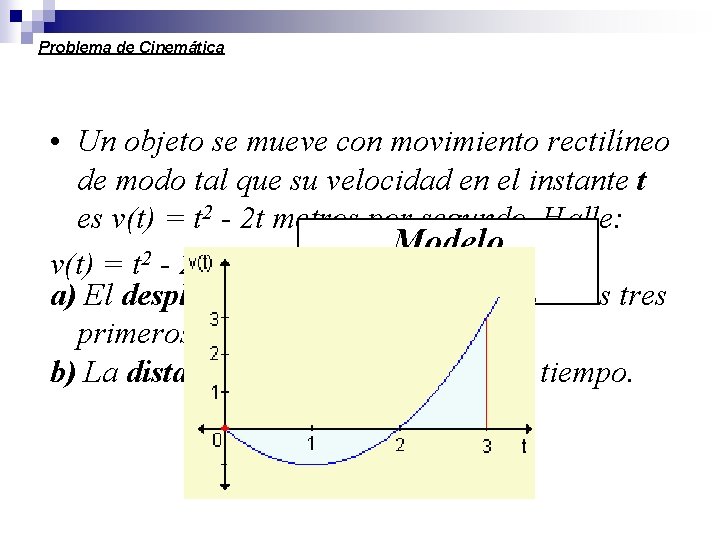
Problema de Cinemática • Un objeto se mueve con movimiento rectilíneo de modo tal que su velocidad en el instante t es v(t) = t 2 - 2 t metros por segundo. Halle: Modelo 2 v(t) = t - 2 t Matemático a) El desplazamiento del objeto durante los tres primeros segundos. b) La distancia recorrida durante ese tiempo.

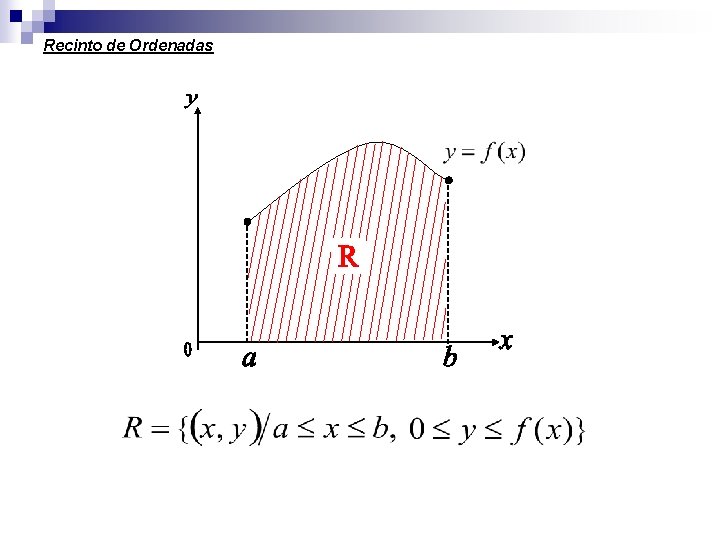
Recinto de Ordenadas

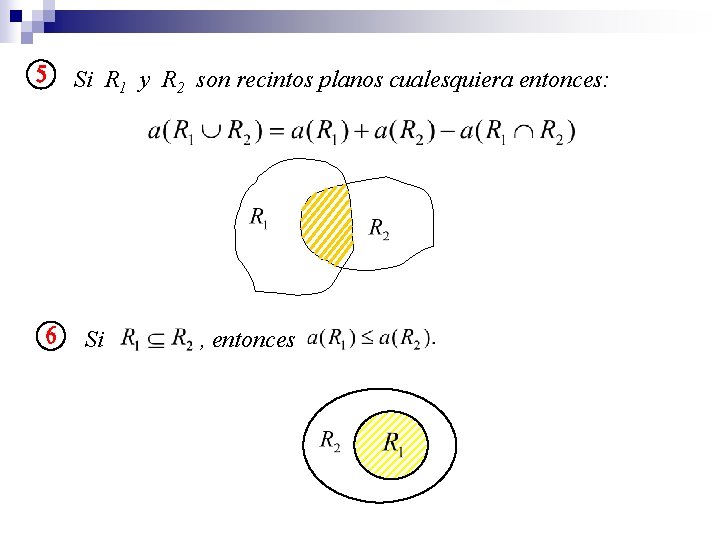
n Propiedades del área Si R es un punto o una curva, entonces a(R) = 0 Si R 1 y R 2 son recintos planos congruentes, entonces a(R 1) = a(R 2). Si R 1 y R 2 son recintos planos cuya intersección tiene área nula, entonces

Si R 1 y R 2 son recintos planos cualesquiera entonces: Si , entonces

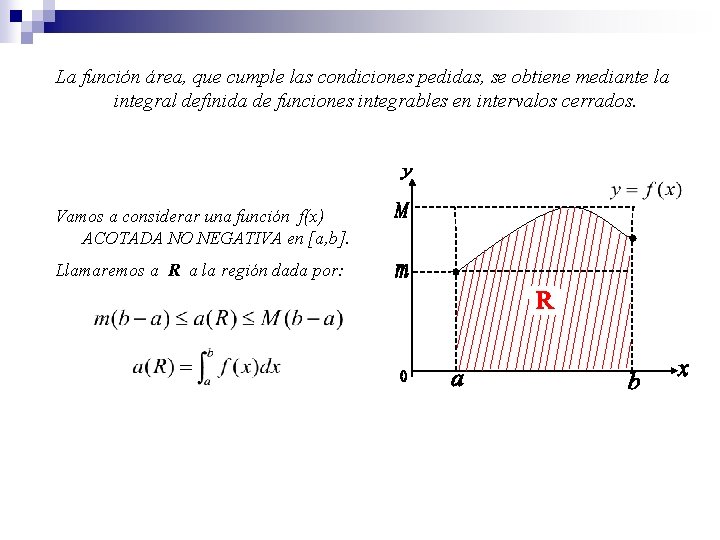
La función área, que cumple las condiciones pedidas, se obtiene mediante la integral definida de funciones integrables en intervalos cerrados. Vamos a considerar una función f(x) ACOTADA NO NEGATIVA en [a, b]. Llamaremos a R a la región dada por:

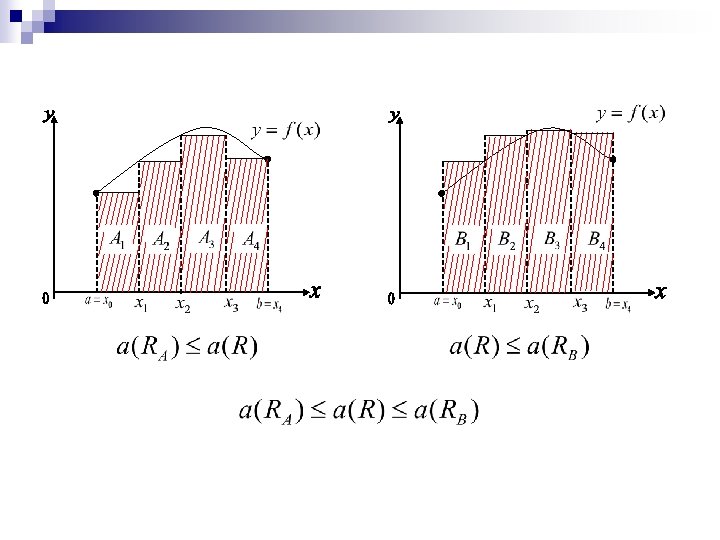
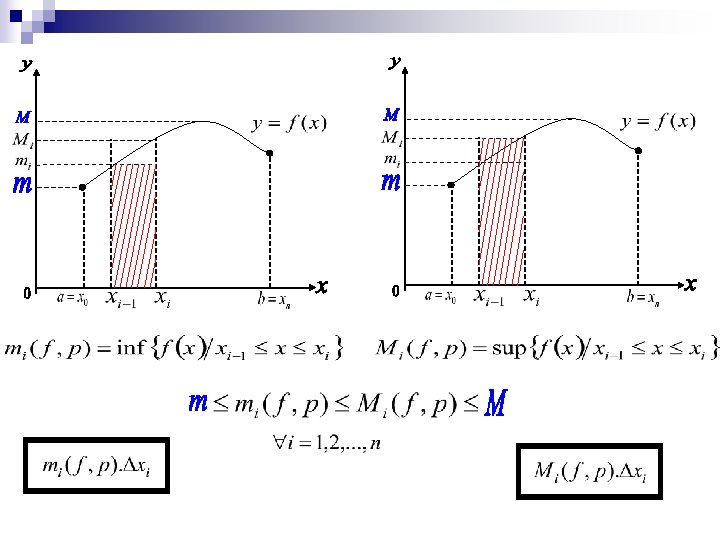
n Sumas Inferiores y Sumas Superiores El intervalo [a, b] queda dividido en n subintervalos , Con i=1, 2, 3, …, n. Donde es la longitud del intervalo i-ésimo. (Nº Real Positivo)

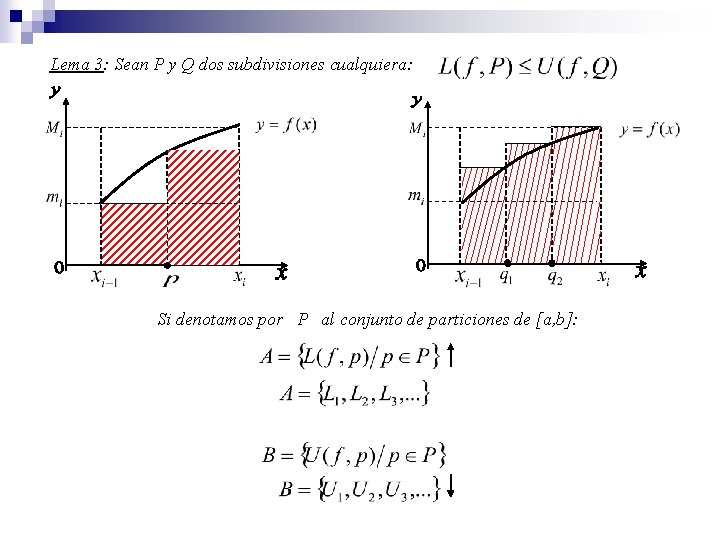
Llamaremos SUMA INFERIOR correspondiente a la partición P. Llamaremos SUMA SUPERIOR correspondiente a la partición P.

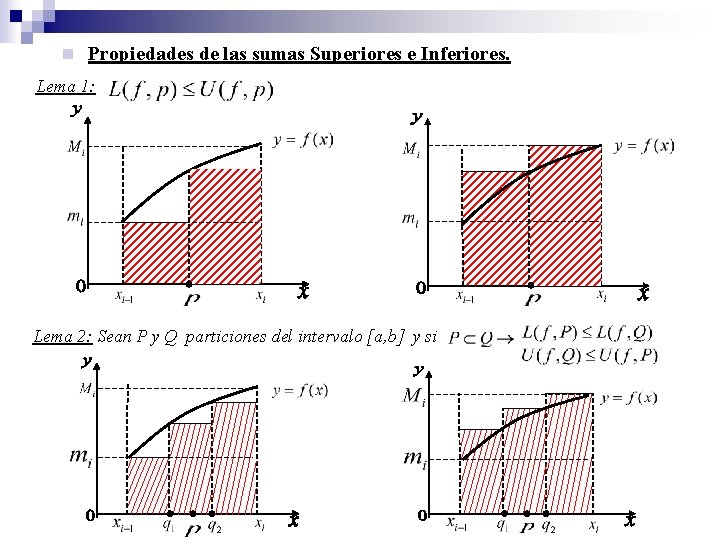
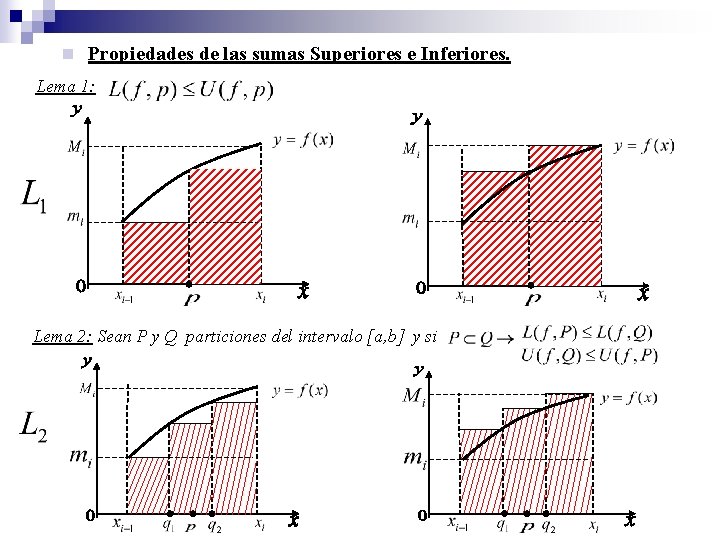
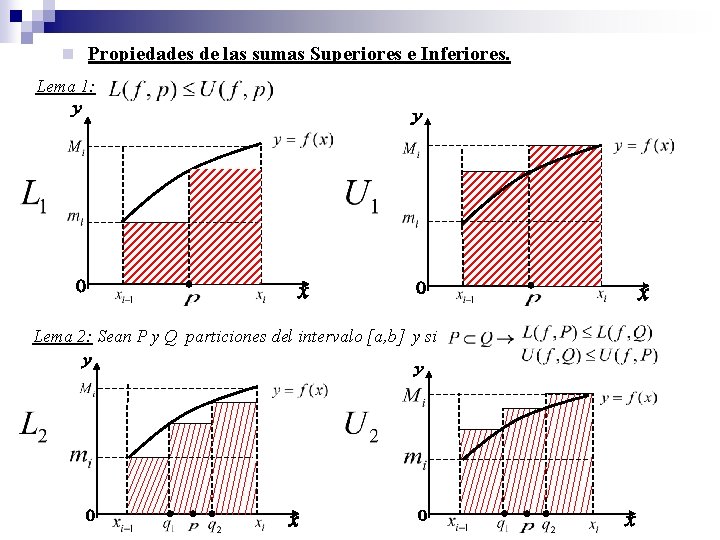
n Propiedades de las sumas Superiores e Inferiores. Lema 1: Lema 2: Sean P y Q particiones del intervalo [a, b] y si

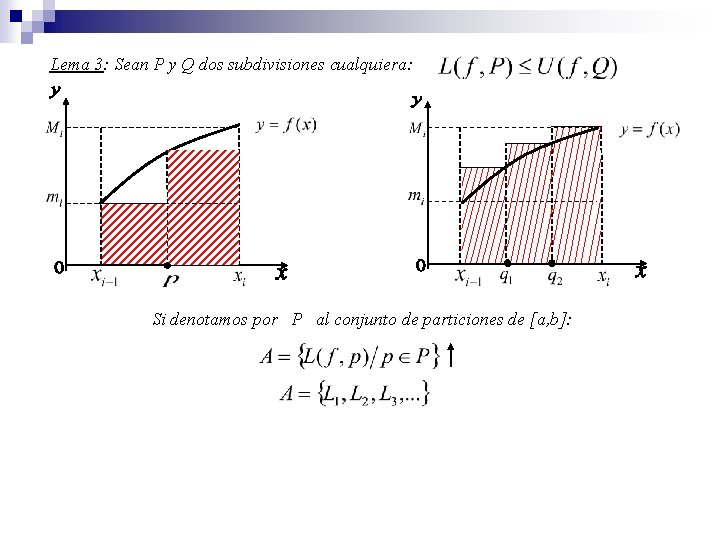
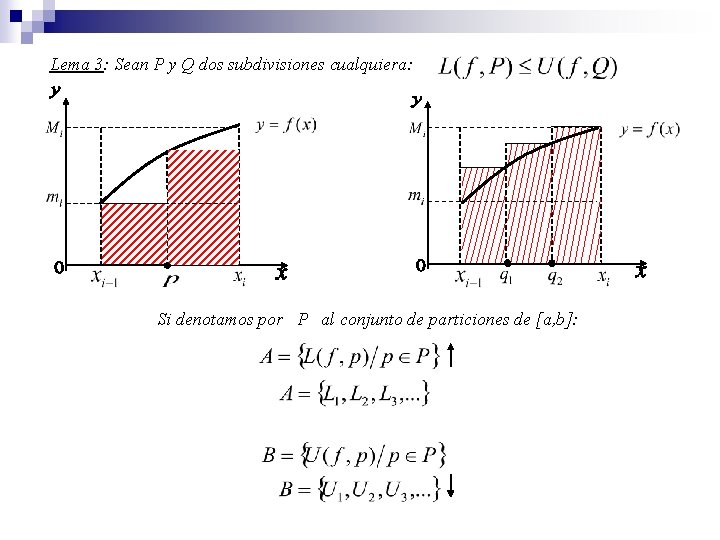
Lema 3: Sean P y Q dos subdivisiones cualquiera: Si denotamos por P al conjunto de particiones de [a, b]:

n Propiedades de las sumas Superiores e Inferiores. Lema 1: Lema 2: Sean P y Q particiones del intervalo [a, b] y si

Lema 3: Sean P y Q dos subdivisiones cualquiera: Si denotamos por P al conjunto de particiones de [a, b]:

n Propiedades de las sumas Superiores e Inferiores. Lema 1: Lema 2: Sean P y Q particiones del intervalo [a, b] y si

Lema 3: Sean P y Q dos subdivisiones cualquiera: Si denotamos por P al conjunto de particiones de [a, b]:

Integral Inferior de f en [a, b] Integral Superior de f en [a, b] Si: = Entonces: El área de la región a(R)= =

Definición: Sea f: [a, b]→R ACOTADA, diremos que f es INTEGRABLE sobre [a, b] si y sólo si En este caso se denota: Se dice que este NUMERO es la INTEGRAL DEFINIDA de f sobre [a, b] según Riemann.

n Teorema: Condición Necesaria y Suficiente para la existencia de: Si la función f esta ACOTADA y DEFINIDA sobre [a, b], → f es INTEGRABLE sobre ese intervalo si y sólo y si P de [a, b] tal que: n Teorema: Condición Suficiente para la existencia de: Si f : [a, b]→ R es continua, entonces f es INTEGRABLE sobre [a, b]

Propiedades Básicas de la Integral Definida Si y f es integrable en [a, b] entonces f es integrable en [a, c] y en [c, b] y Si f es integrable en [a, b] y c es una constante, entonces cf es integrable en [a, b] y Si f y g son integrables en [a, b] entonces f+g es integrable en [a, b] y Si f y g son integrables en [a, b] y para todo , entonces Si f es integrable en [a, b], entonces | f | es integrable en [a, b] y

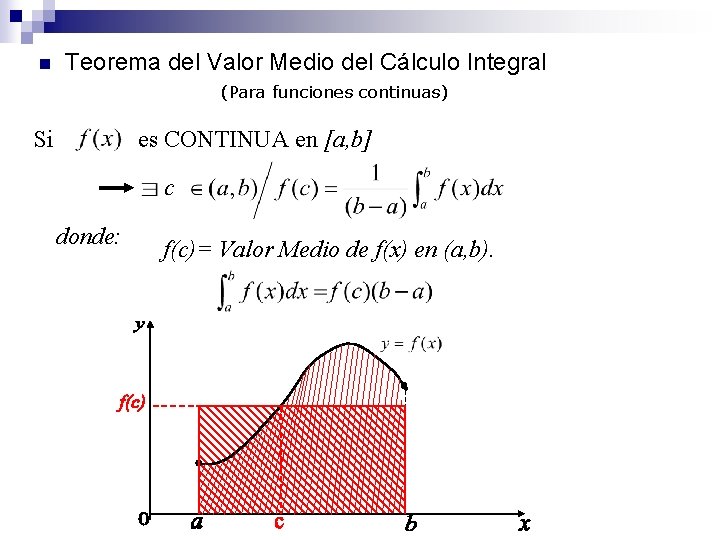
n Teorema del Valor Medio del Cálculo Integral (Para funciones continuas) Si es CONTINUA en [a, b] c donde: f(c)= Valor Medio de f(x) en (a, b).

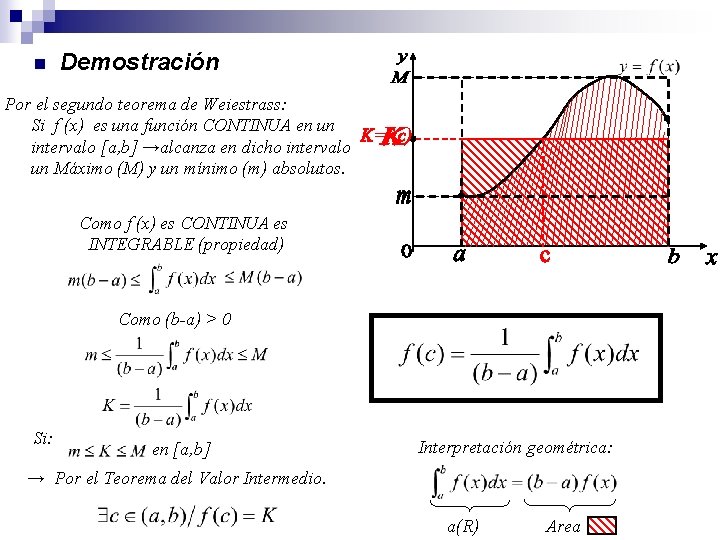
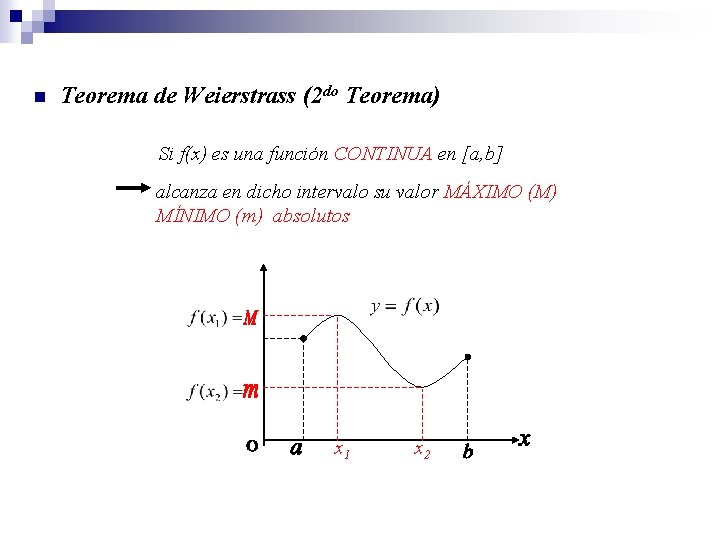
n Demostración Por el segundo teorema de Weiestrass: Si f (x) es una función CONTINUA en un intervalo [a, b] →alcanza en dicho intervalo un Máximo (M) y un mínimo (m) absolutos. Como f (x) es CONTINUA es INTEGRABLE (propiedad) Como (b-a) > 0 Si: en [a, b] Interpretación geométrica: → Por el Teorema del Valor Intermedio. a(R) Area

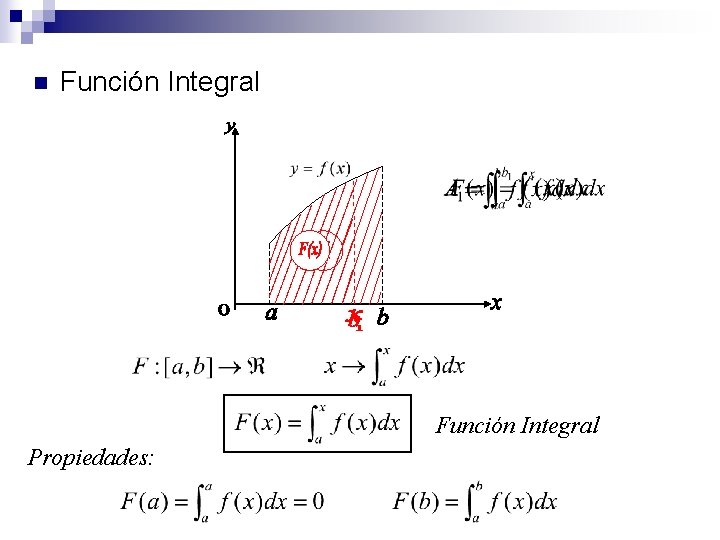
n Función Integral Propiedades:

n Teorema Fundamental del Cálculo Integral Si continua en [a, b], La función integral es DERIVABLE.

n Demostración: Reemplazando en (1) Por el Teorema del Valor Medio del Cálculo Integral:

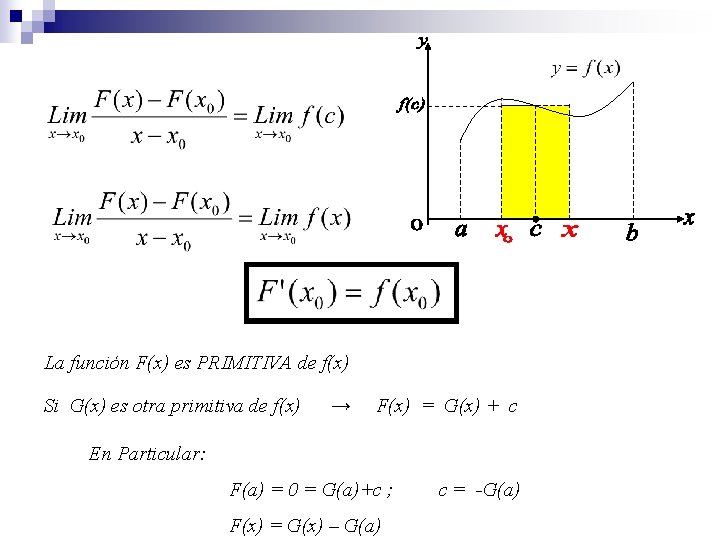
La función F(x) es PRIMITIVA de f(x) Si G(x) es otra primitiva de f(x) → F(x) = G(x) + c En Particular: F(a) = 0 = G(a)+c ; c = -G(a) F(x) = G(x) – G(a)

n Regla de Barrow Sea f(x) CONTINUA en [a, b], G(x) una PRIMITIVA de f(x) Demostración:

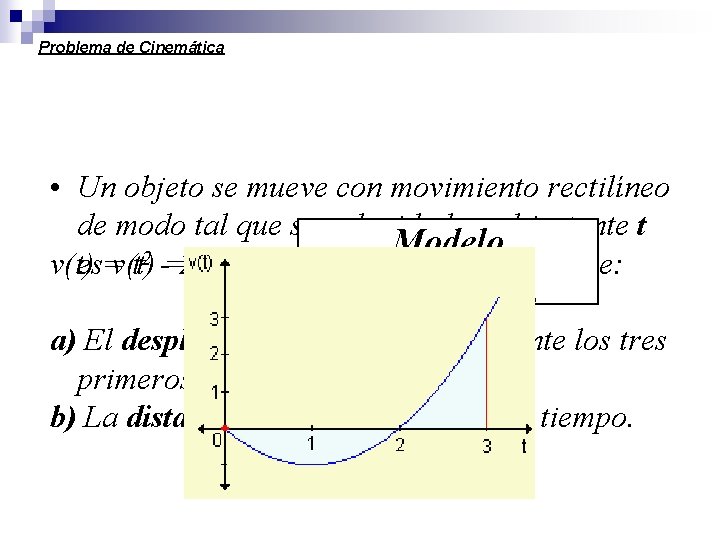
Problema de Cinemática • Un objeto se mueve con movimiento rectilíneo de modo tal que su velocidad en el instante t Modelo 2 2 es v(t) = t - 2 t metros por segundo. Halle: Matemático a) El desplazamiento del objeto durante los tres primeros segundos. b) La distancia recorrida durante ese tiempo.

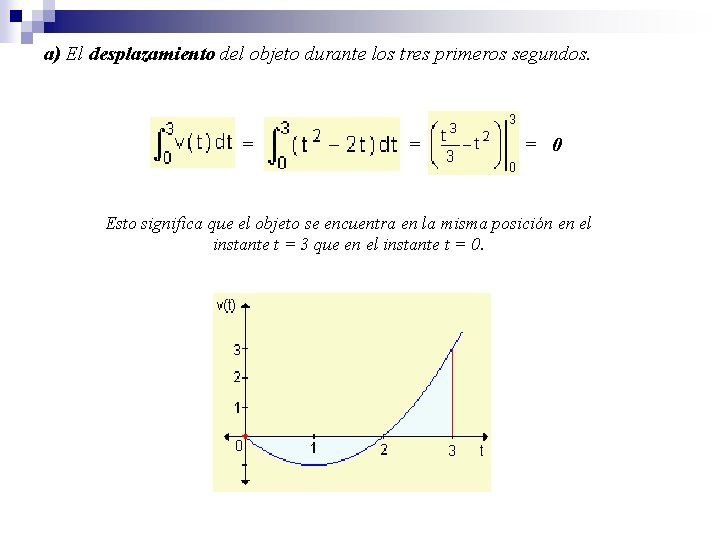
a) El desplazamiento del objeto durante los tres primeros segundos. = = = 0 Esto significa que el objeto se encuentra en la misma posición en el instante t = 3 que en el instante t = 0.

b) La distancia recorrida durante ese tiempo. La velocidad puede escribirse como v(t) = t ( t - 2) de modo que si y la velocidad es negativa si . La distancia recorrida es: = = = Distancia recorrida= = 8/3 Podemos asegurar que la distancia recorrida es de 8/3 metros.

Bibliografía: • RABUFFETTI, H. – Introducción al Análisis Matemático (Cálculo 1) – 10º Edición – Editorial “El Ateneo” – Buenos Aires – Argentina – 1987. • STEWART, J. – Cálculo – Trascendentes Tempranas – 4º Edición – Editorial “Thomson” – Mexico – 2002. • PURCELL, E. , VARBERG, D. – Cálculo con Geometría Analítica – 6º Edición – Editorial “Prentice Hall Hispanoamericana, S. A. ” – Mexico – 1992. • VERA DE PAYER, E. y Otros – Matemática I para Ciencias Naturales – 3º Edición – Editorial “Universitas” – Córdoba – Argentina – 2005.

n Teorema del Valor Intermedio Sea f(x) continua en [a, b] con Si K es un número estrictamente comprendido entre f(a) y f(b) f(a) < K < f(b) c

n Teorema de Weierstrass (2 do Teorema) Si f(x) es una función CONTINUA en [a, b] alcanza en dicho intervalo su valor MÁXIMO (M) MÍNIMO (m) absolutos x 1 x 2