MOVIVMIENTO CIRCULAR Y GRAVITACION Trabajo escrito para la

MOVIVMIENTO CIRCULAR Y GRAVITACION Trabajo escrito para la Asignatura de Física. Docente MIGUEL JARAMILLO VILLA SANTIAGO DE CALI, 2014

Trabajo escrito para la Asignatura de Física. Presentado por : 11 -14 Docente MIGUEL JARAMILLO VILLA SANTIAGO DE CALI, 2014

INTRODUCCION El trabajo presentado a continuación nos muestra el estudio de dos diferentes partes fundamentales del movimiento de nuestro cuerpo, las cuales, de cierto modo tienen una marcada asociación; además, cada una de estas dos componentes tienen un ejemplo de aplicación para un mayor cubrimiento de nuestro tema y de esta forma una mayor comprensión.

OBJETIVOS • Demostrar la importancia de la fisica en el movimiento corporal humano. • Observar los temas resueltos: movimiento circular y gravitacion enfocados en el cuerpo humano. • Comprender la influencia de la fuerza de gravedad en el cuerpo, su accion consecuencias. • Identificar en un movimiento de alguna parte de nuestro cuerpo y sus componentes.

MOVIMIENTO CIRCULAR Se llama movimiento circular Al que describe una partícula material al girar alrededor de un punto, variando constantemente su dirección y su sentido, pero recorriendo arcos iguales en tiempos iguales. En todo cuerpo sujeto a un movimiento circular se dan dos tipos de velocidades: velocidad tangencial y velocidad angular.

PERIODO Tiempo que invierte un cuerpo animado de movimiento circular uniforme en describir una circunferencia completa. T = t/n Conociendo el periodo se puede calcular la velocidad angular w = 2π/T

FRECUENCIA Numero de circunferencias descritas en su trayectoria por cada segundo. Se expresa en revoluciones por segundo. F = n/t = 1/T Conociendo la frecuencia la velocidad angular es: n = numero de giros o vueltas. T = tiempo

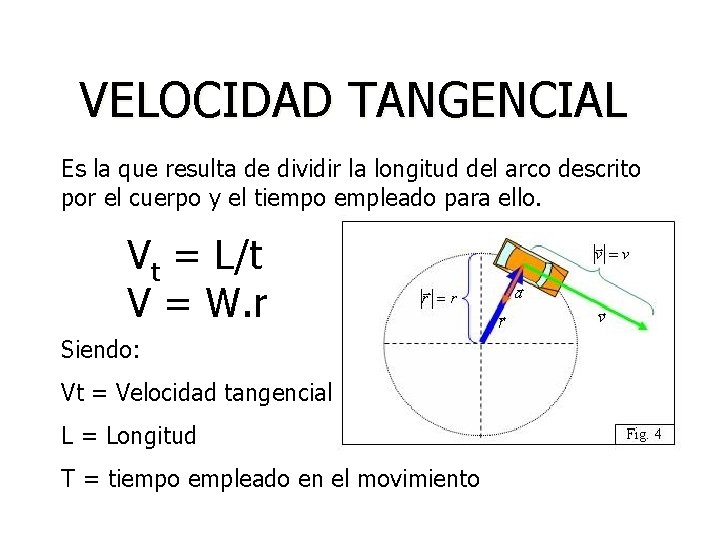
VELOCIDAD TANGENCIAL Es la que resulta de dividir la longitud del arco descrito por el cuerpo y el tiempo empleado para ello. Vt = L/t V = W. r Siendo: Vt = Velocidad tangencial L = Longitud T = tiempo empleado en el movimiento

VELOCIDAD ANGULAR La velocidad angular de un cuerpo es igual al cociente del ángulo a, que describe en su movimiento, dividido por el tiempo que tarda en recorrerlo. En el caso angular, una partícula se mueve en un sentido o en otro a lo largo de su trayectoria circular.

FUERZA CENTRIPETA Fuerza que hace que un cuerpo siga un movimiento circular y significa “hacia el centro”. La intensidad de esta fuerza se obtiene multiplicando la masa del cuerpo por la aceleración que produce. Cuando se hace girar un objeto atado al extremo de una cuerda, esta transmite la fuerza centrípeta que se identifica con la tensión a que está sometida.

La fórmula de la aceleración centrípeta, en función de la velocidad tangencial es: a = V 2/r CUANDO SE EJECUTAN MOVIMIENTOS EN LA DANZA, EL MOVIMIENTO DEL CUERPO ALREDEDOR DE UN EJE SE PRODUCE POR LA EXISTENCIA DE LA ACELERACIÓN CENTRÍPETA, PROVOCADA POR EL CUERPO QUE SE MUEVE.

Un brazo realiza un desplazamiento angular de 0. 75 radianes, si este desplazamiento tardó 0. 3 s. ¿cuál es la velocidad angular promedio del brazo?

R- Para contestar esta pregunta usamos la ecuacion: w = φ/t Y sustituyendo los valores conocidos : w = 0. 75 Radianes = 2. 5 Rad/s 0. 3 s

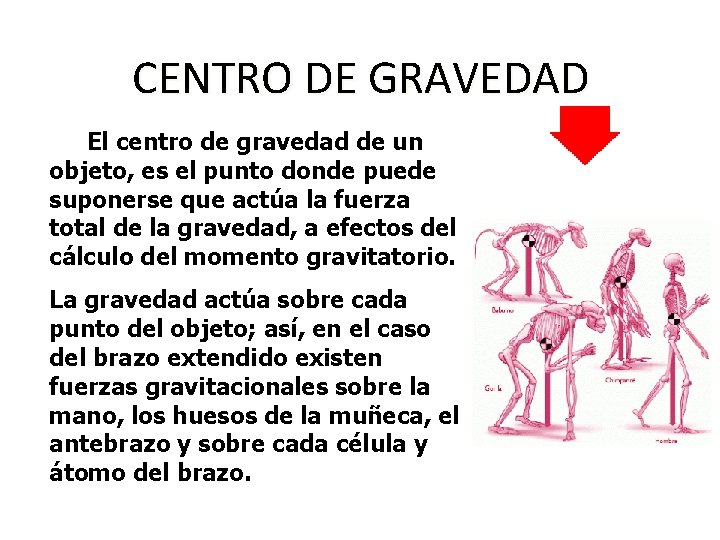
CENTRO DE GRAVEDAD El centro de gravedad de un objeto, es el punto donde puede suponerse que actúa la fuerza total de la gravedad, a efectos del cálculo del momento gravitatorio. La gravedad actúa sobre cada punto del objeto; así, en el caso del brazo extendido existen fuerzas gravitacionales sobre la mano, los huesos de la muñeca, el antebrazo y sobre cada célula y átomo del brazo.

La suma de todas estas fuerzas es la fuerza total de la gravedad sobre el brazo, y la suma de estos momentos es el momento total debido a la gravedad. Un cierto número de rasgos característicos del centro de gravedad: 1 – La fuerza de gravedad sobre un objeto produce un momento nulo alrededor de su centro de gravedad, por que la linea de accion de la fuerza de la gravedad pasa por el centro de gravedad y así, la distancia del centro de gravedad a esta linea es cero:

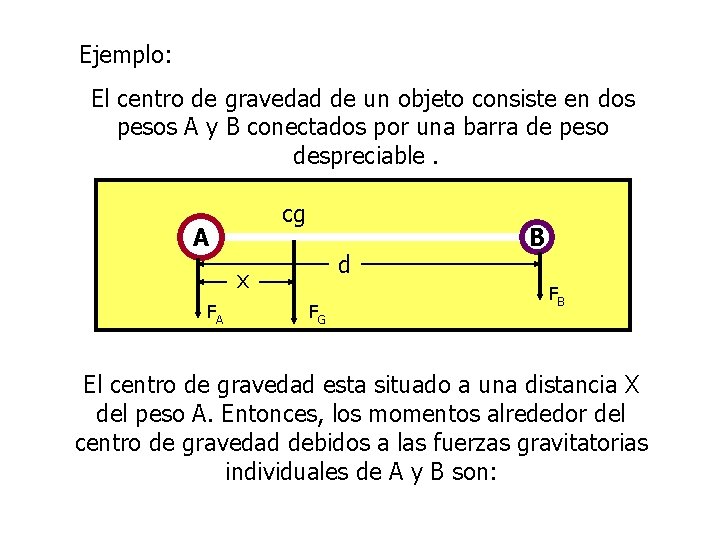
Ejemplo: El centro de gravedad de un objeto consiste en dos pesos A y B conectados por una barra de peso despreciable. cg A d x FA FG B FB El centro de gravedad esta situado a una distancia X del peso A. Entonces, los momentos alrededor del centro de gravedad debidos a las fuerzas gravitatorias individuales de A y B son:

TA = F A x y TB = - FB (d – x) Como el momento total alrededor del centro de gravedad debido a las fuerzas gravitatorias es nulo, se obtiene: FAx – FB(d – x) = 0 FB d X = F A + FB

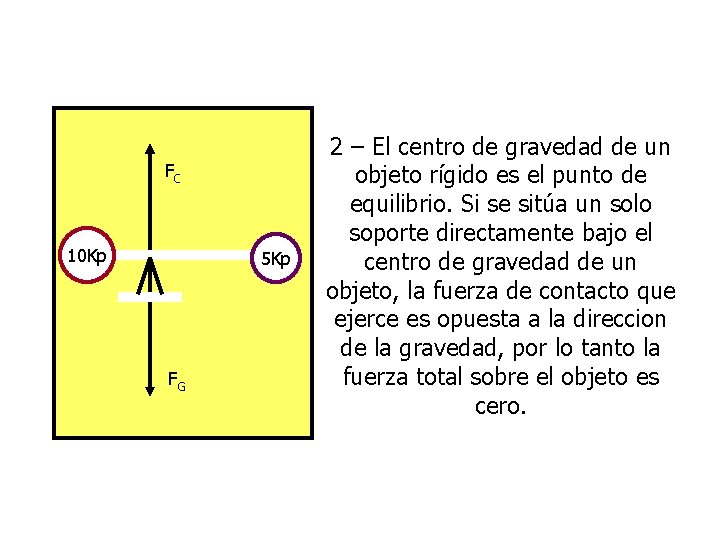
FC 10 Kp 5 Kp FG 2 – El centro de gravedad de un objeto rígido es el punto de equilibrio. Si se sitúa un solo soporte directamente bajo el centro de gravedad de un objeto, la fuerza de contacto que ejerce es opuesta a la direccion de la gravedad, por lo tanto la fuerza total sobre el objeto es cero.

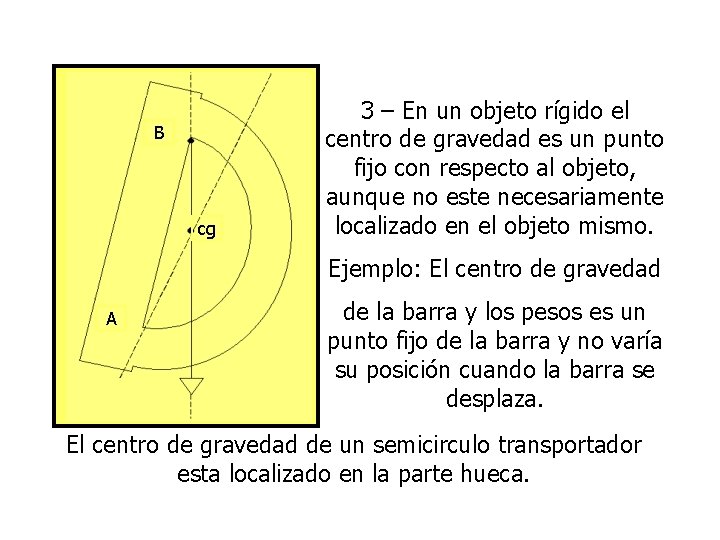
B cg 3 – En un objeto rígido el centro de gravedad es un punto fijo con respecto al objeto, aunque no este necesariamente localizado en el objeto mismo. Ejemplo: El centro de gravedad A de la barra y los pesos es un punto fijo de la barra y no varía su posición cuando la barra se desplaza. El centro de gravedad de un semicirculo transportador esta localizado en la parte hueca.

4 – En un objeto flexible, como el cuerpo humano, la posición del centro de gravedad varía cuando el objeto cambia de forma. El centro de gravedad de un hombre, que permanece de pie y derecho, esta localizado al nivel de la segunda vértebra sacra sobre una línea vertical que toca el suelo a unos 3 cm por delante de la articulación del tobillo. cg Si el hombre levanta los brazos sobre su cabeza, el centro de gravedad subirá varios cms.

Ejemplo: Durante un salto de altura el centro de gravedad queda totalmente fuera del cuerpo. La capacidad para variar la posición del centro de gravedad del cuerpo es de importancia crítica para mantener el equilibrio mientras caminamos y en la ejecución, con éxito de muchas acciones atléticas.

EQUILIBRIO: El principio del equilibrio requiere que el centro de gravedad del cuerpo en posición firme esté en la línea vertical que pasa por algún punto dentro del área de apoyo definida por la posición de los pies.

Ejemplo: Cuando una persona se inclina para tocar la punta de los pies sin doblar las rodillas, su centro de gravedad tiende a moverse hacia delante, mas alla del area de contacto. Para evitar esto, sus piernas y nalgas se mueven hacia atrás, con lo cual el cuerpo permanece en equilibrio sobre los pies.

Se puede demostrar esto, intentando tacar las puntas de los pies con los talones y la espalda pegados a la pared. La pared impide que el cuerpo mantenga el centro de gravedad por encima del area de contacto y, por lo tanto, no se puede mantener el equilibrio. Al levantar un pie del suelo, el centro de gravedad del cuerpo tiene que desplazarse por encima del pie apoyado, esto exige que todo el cuerpo se mueva lateralmente. Al andar, el cuerpo se bambolea de un lado a otro para mantener el centro de gravedad sobre un área de apoyo en contínuo movimiento.

Una buena estabilidad se obtiene teniendo el centro de gravedad de un objeto en una posicion baja por encima de un área de sustentacion grande. Para un cuadrupedo, el área de apoyo es el área que hay entre las cuatro patas, lo cual hace que el animal tenga una gran estabilidad GUSANO ANFIBIO REPTIL MAMIFERO HOMBRE Representación esquemática del incremento filogénico de la altura del centro de gravedad de los animales por encima de su superficie de sustentación

La inestabilidad resultante permite a los animales moverse mas rapidamente, pero requiere un control neuromuscular complejo para mantener el equilibrio. Mientras una persona esta en pie, unos receptores cinestésicos detectan los pequeños cambios de posición del centro de gravedad y se hacen los necesarios ajustes en los músculos del cuerpo para que el centro de gravedad vuelva al centro del area de sustentación. La posición humana es mecánicamente tan inestable que a un niño le cuesta un año desarrollar el control neuromuscular suficiente para permanecer en pie sin ayuda.

¿Dónde se halla el centro de gravedad de un hombre de 82 Kp cuando está en pie de modo que la fuerza sobre su pie izquierdo herido, no sobrepase los 20 Kp?

R- Se dtermino que los pies están a 30 cm uno del otro, para encontrar el centro de gravedad, conocemos que FL (fuerza del pie izquierdo) = 20 Kp; la distancia d del centro de gravedad al pie izquierdo es desconocida. Obtenemos de nuevo que FR (fuerza del pie derecho) = 62 Kp; por lo tanto los momentos alrededor de O (punto donde actúa FL sobre el pie izquierdo) son : TL = 20 kp X 0 = 0 TR = -62 Kp X 0. 30 m = -18, 6 Kp-m TG = 82 Kp X d

la suma es: -18, 6 Kp-m + 82 Kp x d =0 Así, la posición del centro de gravedad es: d= + 18, 6 Kp-m 82 Kp = 0. 225 m Compárese este ejemplo con el de un columpio, mientras que las circunstancias son distintas, la física básica es la misma: en los dos problemas las tres fuerzas paralelas son las mismas con tres lineas de accion, áctuan sobre un objeto en equilibrio.

CONCLUSIONES • El movimiento circular uniforme tiene como elementos fundamentales el periodo, la frecuencia, la velocidad angular, velocidad lineal o tangencial y la aceleración centrípeta. . • Definimos el centro de gravedad como punto de apoyo para el equilibrio dinámico del cuerpo humano. • El centro de gravedad se reacomoda de acuerdo a la posición del cuerpo con respecto a la vertical.

BIBLIOGRAFIA • Lea, susan M. /Fisica : La naturaleza de las cosas/2 v. /Mexico. Thompson, 1999. • Cromer, Alan H. 1935/Fisica para las ciencias de la vida/ 2 a. edicion/Mexico. Thompson, 1998. • Kane, Joseph W. /Fisica. /XXI edicion/Barcelona. Reverte, 1998. • Feynman, Richard Philips, 1918 – 1998/ Seis piezas faciles: La fisica explicada por un genio/Barcelona. Critica, 1998. • Hacyan, Shahen/ Relatividad para principiantes/2 a. Edicion/ Mexico. Fondo de cultura economica, 2000 • Le Veau, Barney/ Biomecanica del cuerpo humano : Williams y Lissner/ Mexico. Trillas, 1991.