TEMA VII ESQUEMA GENERAL Definicin general Clasificacin Diseo

TEMA VII

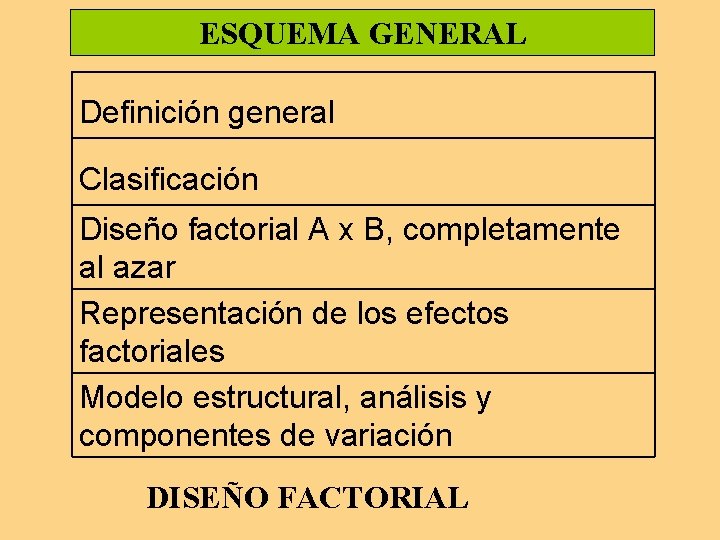
ESQUEMA GENERAL Definición general Clasificación Diseño factorial A x B, completamente al azar Representación de los efectos factoriales Modelo estructural, análisis y componentes de variación DISEÑO FACTORIAL

Concepto El diseño factorial, como estructura de investigación, es la combinación de dos o más diseños simples (o unifactoriales); es decir, el diseño factorial requiere la manipulación simultánea de dos o más variables independientes (llamados factores), en un mismo experimento. . . //. .

En función de la cantidad de factores o variables de tratamiento, los formatos factoriales se denominan, también, diseños de tratamientos x tratamientos, etc, y se simbolizan por Ax. B, Ax. Bx. C, etc.

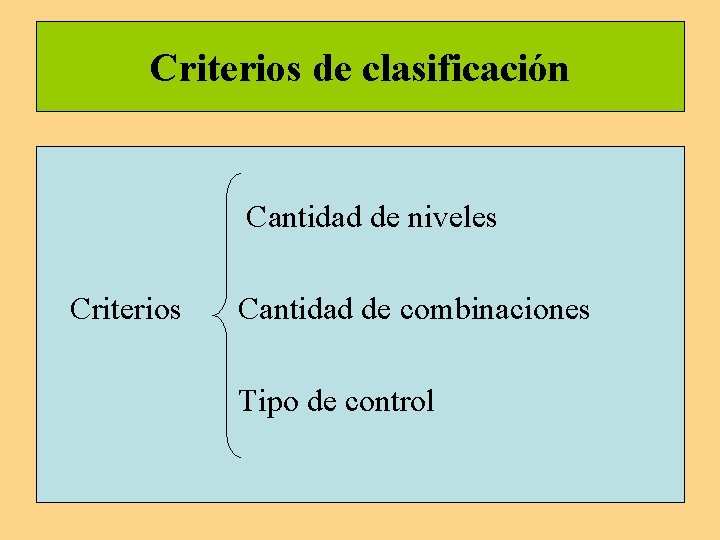
Criterios de clasificación Cantidad de niveles Criterios Cantidad de combinaciones Tipo de control

Clasificación del diseño factorial por criterio A) Según la cantidad de niveles o valores por factor, el diseño factorial se clasifica en: Cantidad constante Cantidad de valores Cantidad variable

La notación del diseño es más sencilla cuando la cantidad de niveles por factor es igual (es decir, constante). Así, el diseño factorial de dos factores a dos niveles se representa por 2², el de tres factores por 23, etc. En términos generales, los diseños a dos niveles y con k factores se representan por 2 k; a tres niveles, por 3 k; a cuatro niveles por 4 k, etc. . . //. .

Cuando los factores actúan a más de dos niveles (es decir, cuando la cantidad de valores por factor es variable), el diseño se representa por 2 x 3, 2 x 3 x 4, etc. A su vez, cabe considerar la posibilidad de que, tanto en un caso como en otro, el diseño sea balanceado (proporcionado) o no balanceado (no proporcionado); es decir, diseños con igual cantidad de sujetos por casilla y diseños con desigual cantidad de sujetos por casilla.

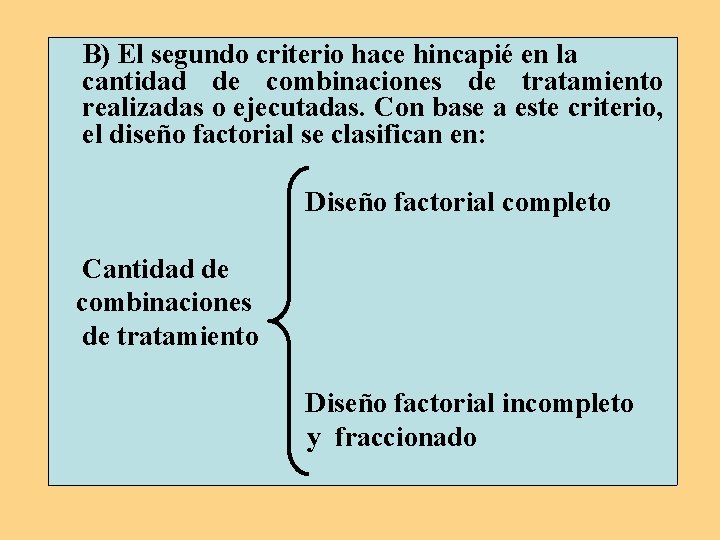
B) El segundo criterio hace hincapié en la cantidad de combinaciones de tratamiento realizadas o ejecutadas. Con base a este criterio, el diseño factorial se clasifican en: Diseño factorial completo Cantidad de combinaciones de tratamiento Diseño factorial incompleto y fraccionado

Si el diseño factorial es completo, se realizan todas las posibles combinaciones entre los valores de las variables. Así, cada combinación de tratamientos determina un grupo experimental (grupo de tratamiento o casilla). Por ejemplo, el diseño factorial completo 2 x 2 determina cuatro grupos de tratamiento; un diseño 3 x 3 nueve grupos, etc. . . //. .

Asumiendo que sólo se ejecute una parte del total de las combinaciones, el diseño factorial es incompleto o fraccionado, según el procedimiento seguido.

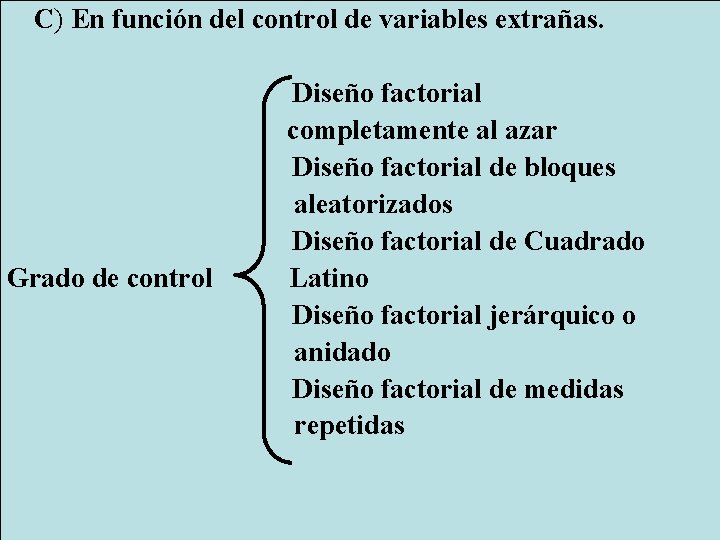
C) En función del control de variables extrañas. Grado de control Diseño factorial completamente al azar Diseño factorial de bloques aleatorizados Diseño factorial de Cuadrado Latino Diseño factorial jerárquico o anidado Diseño factorial de medidas repetidas

Según el control de los factores extraños y la reducción de la variancia del error, el diseño factorial puede ser, en primer lugar, completamente al azar; es decir, aquel formato donde sólo se aplica el azar como técnica de control y donde los grupos se forman mediantelaasignaciónaleatoriadelossujetos. . . //. .

En segundo lugar, el diseño factorial de bloques aleatorizados permite el control de una variable extraña. Según esa estrategia, cada bloque es un réplica completa del experimento, y los grupos intra bloque (dentro de cada bloque) se forman al azar. . . //. .

Siguiendo con el criterio de bloques, el diseño factorial de Cuadrado Latino o de doble sistema de bloques controla dos fuentes de variación extrañas, aunque sólo se realiza una parte del total de combinaciones. . . //. .

El diseño factorial jerárquico o anidado requiere la manipulación experimental de la variable y, al mismo tiempo, la anidación (o inclusión) de una variable dentro de las combinacionesdetratamientosdelosfactores. . . //. .

Por último, el diseño factorial de medidas repetidas incorpora la técnica intra-sujeto; es decir, el sujeto actúa de control propio y recibe todas las combinaciones de tratamiento generados por la estructura factorial.

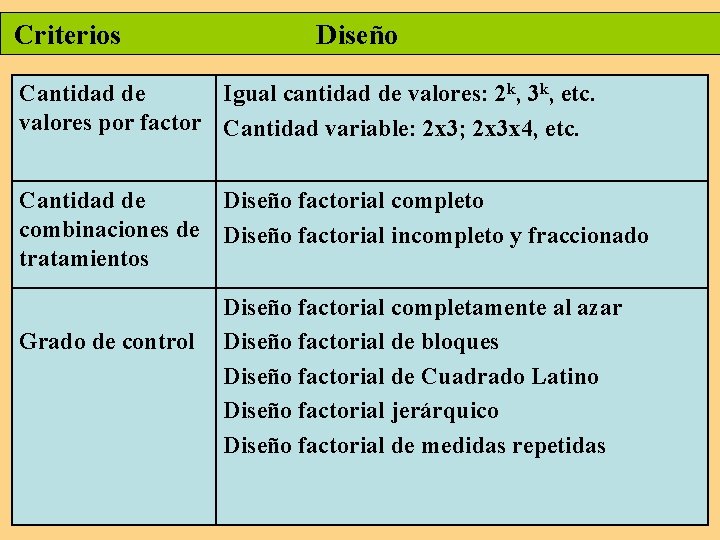
Criterios Diseño Cantidad de Igual cantidad de valores: 2 k, 3 k, etc. valores por factor Cantidad variable: 2 x 3; 2 x 3 x 4, etc. Cantidad de Diseño factorial completo combinaciones de Diseño factorial incompleto y fraccionado tratamientos Grado de control Diseño factorial completamente al azar Diseño factorial de bloques Diseño factorial de Cuadrado Latino Diseño factorial jerárquico Diseño factorial de medidas repetidas

Efectos factoriales estimables 1. Efectos simples 2. Efectos principales 3. Efectos secundarios

Efectos factoriales simples Es posible definir el efecto factorial simple como el efecto puntual de una variable independiente o factor para cada valor de la otra.

Efectos factoriales principales Los efectos factoriales principales, a diferencia de los simples, son el impacto global de cada factor considerado de forma independiente, es decir, el efecto global de un factor se deriva del promedio de los dos efectos simples.

Efectos factoriales secundarios El efecto secundario o de interacción se define por la relación entre los factores o variables independientes, es decir, el efecto cruzado.

Diseño factorial al azar 2 x 2

Estructura del diseño

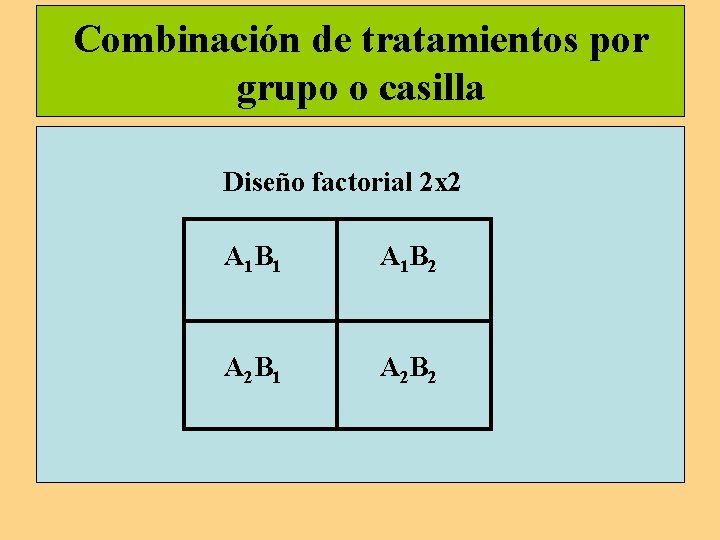
Combinación de tratamientos por grupo o casilla Diseño factorial 2 x 2 A 1 B 1 A 1 B 2 A 2 B 1 A 2 B 2

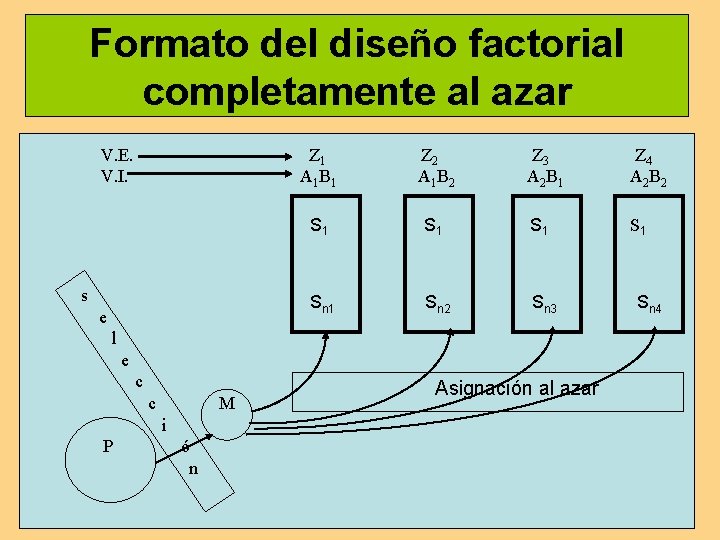
Formato del diseño factorial completamente al azar V. E. V. I. s e Z 1 A 1 B 1 Z 2 A 1 B 2 Z 3 A 2 B 1 Z 4 A 2 B 2 S 1 S 1 Sn 2 Sn 3 l e c c M i P ó n Asignación al azar Sn 4

Caso paramétrico. Ejemplo 1 Se pretende probar, en una situación de aprendizaje discriminante animal, si la magnitud del incentivo (variable incentivo) actúa según el aprendizaje sea simple o complejo (variable dificultad de aprendizaje o variable tarea). En esta hipótesis se afirma que a mayor incentivo, más acusada es la diferencia entre las dos tareas (simple o compleja). . . //. .

Para ello, se registra la cantidad de discriminaciones correctas (variable dependiente) en función de un criterio general de aprendizaje, que asume como suficientes 15 ensayos. Se toma, como medida de la variable dependiente o de respuesta, la cantidad de respuestas correctas, para un máximo de 15, bajo el supuesto de que cada discriminación correcta tiene la misma dificultad de aprendizaje. . . //. .

Para probar la hipótesis propuesta se asignan 32 sujetos, de una muestra experimental, a las combinaciones de tratamientos o casillas (ocho sujetos por casilla), de forma totalmente aleatoria.

Modelo de prueba de hipótesis Paso 1. Según la estructura del diseño son estimables tres efectos. Por esa razón, se plantean tres hipótesis de nulidad relativas a la variable A, variable B e interacción: H 0: α 1 = α 2 = 0 H 0: ß 1 = ß 2 = 0 H 0: (αß)11 = (αß)12 = (αß)21 = (αß)22 = 0

Paso 2. Por hipótesis experimental, se espera que los efectos principales y el de la interacción sean significativos. Estas hipótesis se representan, al nivel estadístico, por H 1: α 1 α 2, o no todas las α son cero H 1: ß 1 ß 2, o no todas las ß son cero H 1: (αß)11 (αß)12 (αß)21 (αß)22, o no todas las αß son cero.

Paso 3. El estadístico de la prueba es la F de Snedecor, con un α de 0. 05, para las tres hipótesis de nulidad. El tamaño de la muestra experimental es N = 32 y el de las submuestras n = 8. Paso 4. Cálculo del valor empírico de las razones F. Para ello, se toma, de nuevo, la matriz de datos del experimento.

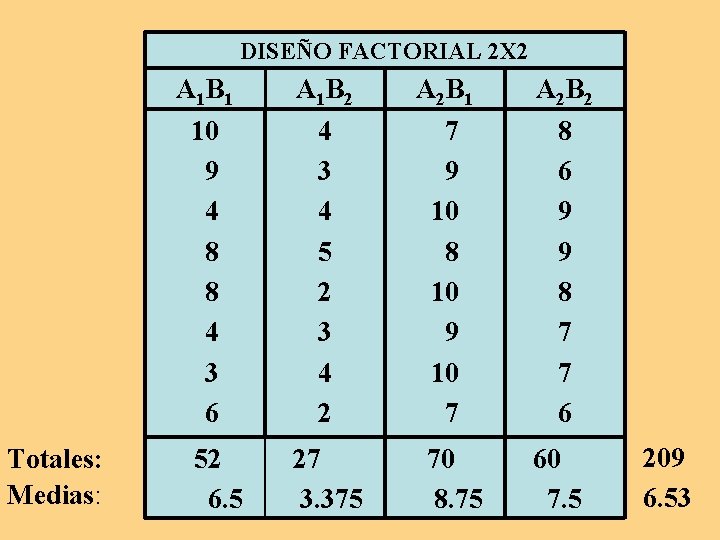
DISEÑO FACTORIAL 2 X 2 A 1 B 1 10 9 4 8 8 4 3 6 Totales: Medias: 52 6. 5 A 1 B 2 4 3 4 5 2 3 4 2 27 3. 375 A 2 B 1 7 9 10 8 10 9 10 7 70 8. 75 A 2 B 2 8 6 9 9 8 7 7 6 60 7. 5 209 6. 53

ANOVA factorial

MODELO ESTRUCTURAL DEL AVAR: DISEÑO FACTORIAL 2 X 2

Especificación del modelo Yijk = la puntuación del i sujeto bajo la combinación del j valor del factor A y el k valor del factor B. μ = la media común a todos los datos del experimento. αj = el efecto o impacto de j nivel de la variable de tratamiento A. ßk = efecto del k valor de la variable de tratamiento B. (αß)jk = efecto de la interacción entre el i valor de A y el k valor de B. εij = error experimental o efecto aleatorio de muestreo.

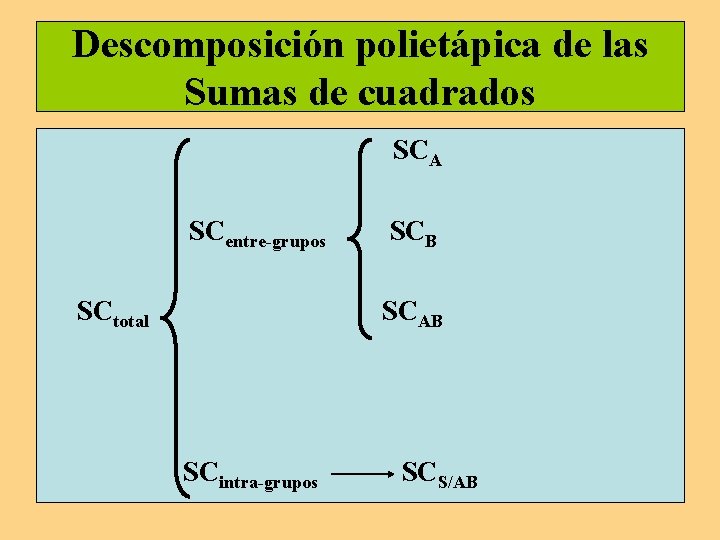
Descomposición polietápica de las Sumas de cuadrados SCA SCentre-grupos SCtotal SCB SCAB SCintra-grupos SCS/AB

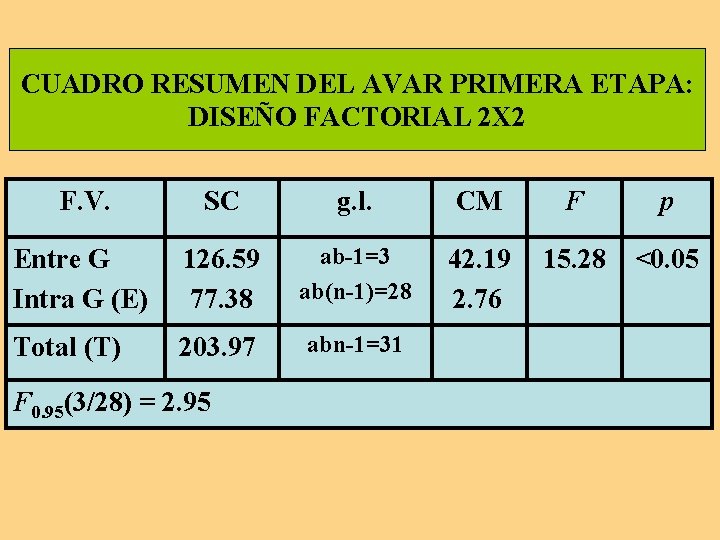
CUADRO RESUMEN DEL AVAR PRIMERA ETAPA: DISEÑO FACTORIAL 2 X 2 F. V. SC g. l. CM F p Entre G Intra G (E) 126. 59 77. 38 ab-1=3 ab(n-1)=28 42. 19 2. 76 15. 28 <0. 05 Total (T) 203. 97 abn-1=31 F 0. 95(3/28) = 2. 95

Inferencia del primer análisis Del primer análisis se concluye que los grupos de tratamiento o experimentales difieren significativamente entre sí; la probabilidad de que un valor F de 15. 28 ocurra al azar es menor que el riesgo asumido (α = 0. 05). . . //. .

En consecuencia, se procede a determinar las causas de esa significación. Nótese que este análisis no obedece a ningún propósito de investigación, ya que sólo sirve para detectar si, en términos globales, hay o no diferencia entre los grupos. De hecho, es como si se hubiera aplicado un modelo uni-factorial de la variancia.

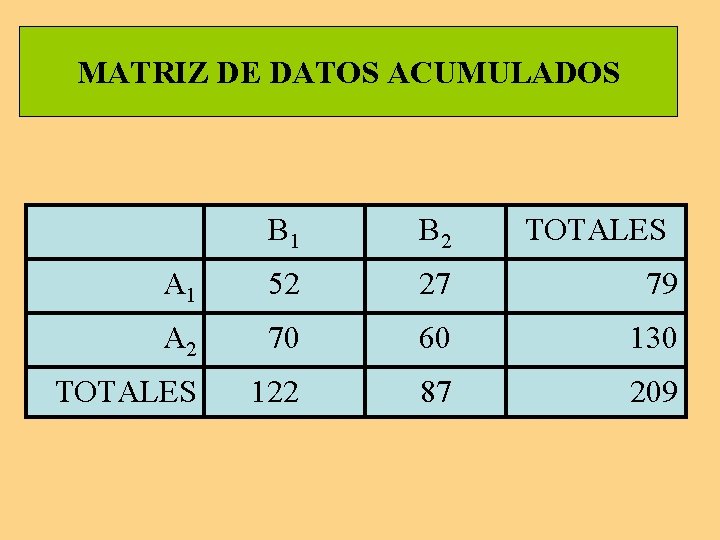
Cálculo de las Sumas de Cuadrados: segunda etapa SCentre-grupos = SCfactor A + SCfactor B + SCinteracción Ax. B El cálculo de estas Sumas de Cuadrados requiere la previa construcción de la tabla de los totales por columnas.

MATRIZ DE DATOS ACUMULADOS B 1 B 2 TOTALES A 1 52 27 79 A 2 70 60 130 TOTALES 122 87 209

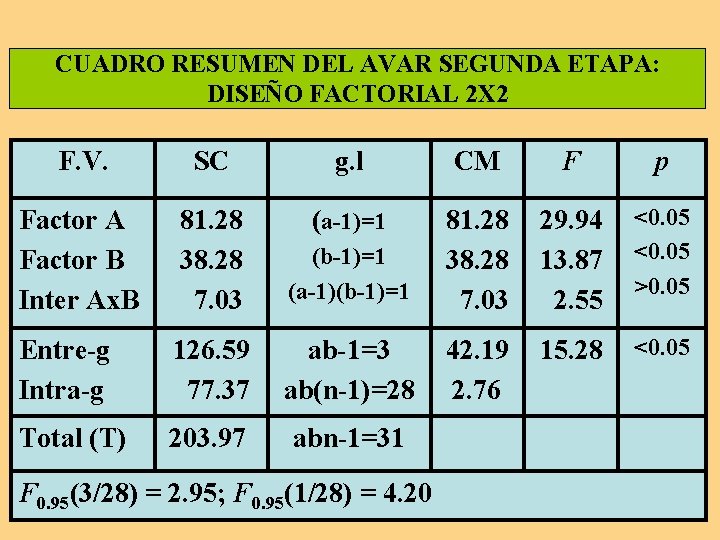
CUADRO RESUMEN DEL AVAR SEGUNDA ETAPA: DISEÑO FACTORIAL 2 X 2 F. V. SC g. l CM F p Factor A Factor B Inter Ax. B 81. 28 38. 28 7. 03 (a-1)=1 (b-1)=1 (a-1)(b-1)=1 81. 28 38. 28 7. 03 29. 94 13. 87 2. 55 <0. 05 >0. 05 Entre-g Intra-g 126. 59 77. 37 ab-1=3 ab(n-1)=28 42. 19 2. 76 15. 28 <0. 05 Total (T) 203. 97 abn-1=31 F 0. 95(3/28) = 2. 95; F 0. 95(1/28) = 4. 20

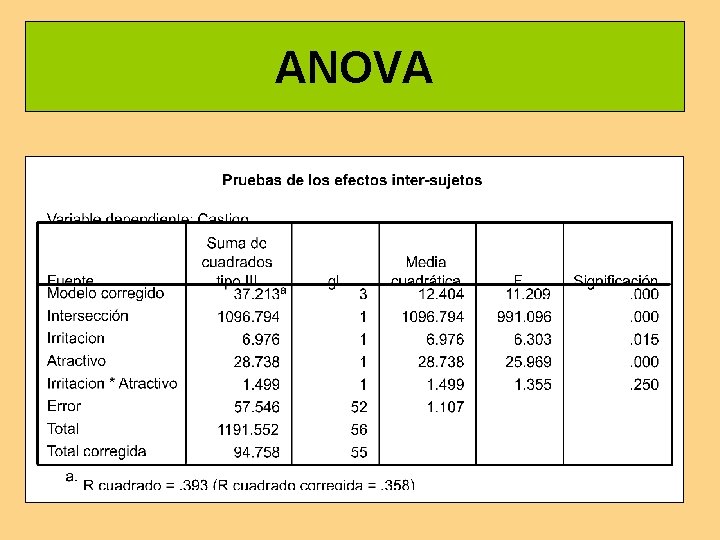
Inferencia del segundo análisis Paso 5. De los resultados del análisis se infiere la no-aceptación de las hipótesis de nulidad para los efectos principales de A y B, con riesgo de error del 5 por ciento. En cambio, se acepta la hipótesis de nulidad para la interacción. En suma, sólo se deriva la significación de los efectos principales.

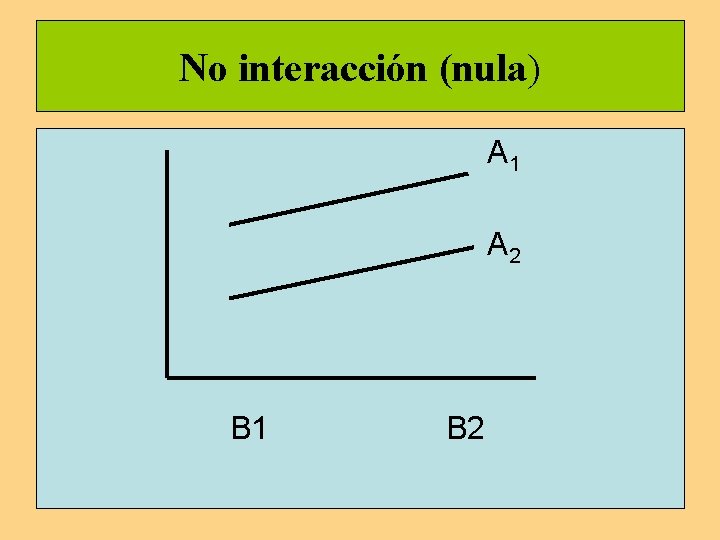
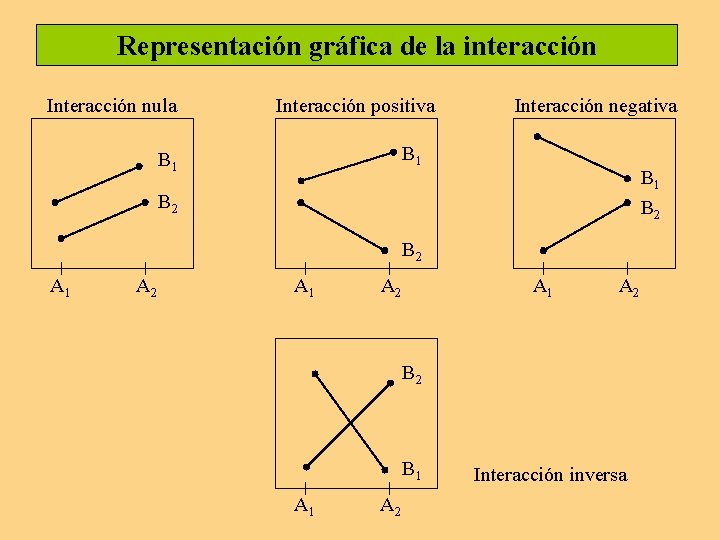
No interacción (nula) A 1 A 2 B 1 B 2

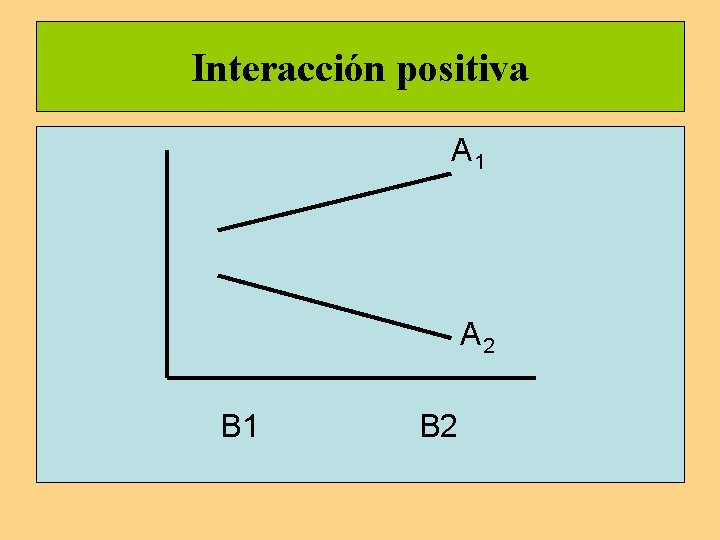
Interacción positiva A 1 A 2 B 1 B 2

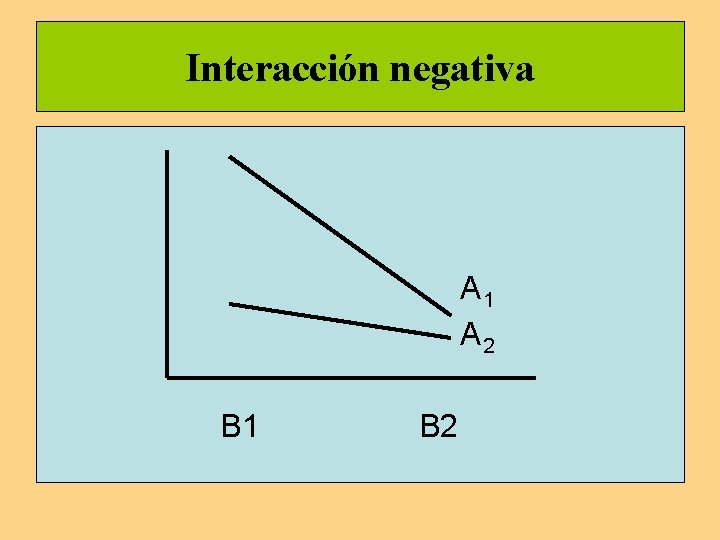
Interacción negativa A 1 A 2 B 1 B 2

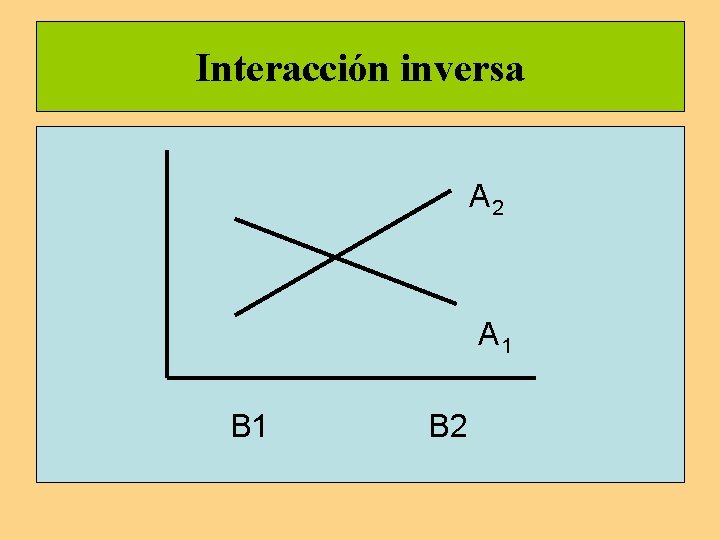
Interacción inversa A 2 A 1 B 2

Representación gráfica de la interacción Interacción nula Interacción positiva Interacción negativa B 1 B 1 B 2 B 2 A 1 A 2 B 1 A 2 Interacción inversa

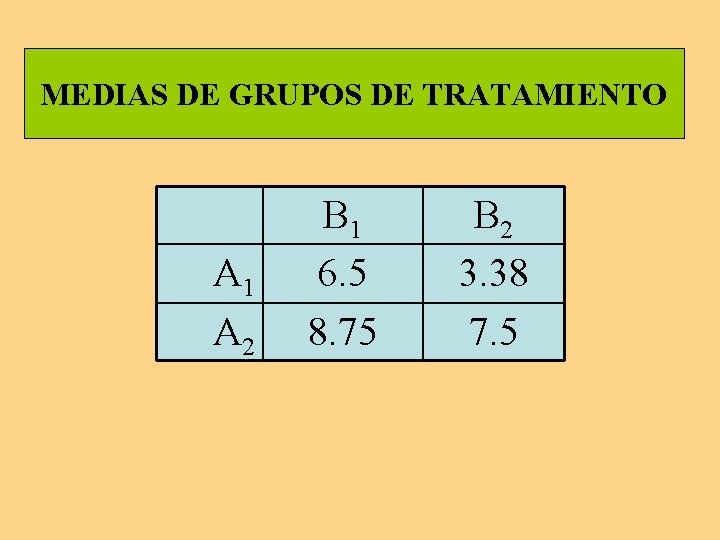
MEDIAS DE GRUPOS DE TRATAMIENTO A 1 A 2 B 1 6. 5 8. 75 B 2 3. 38 7. 5

GRÁFICO INTERACCIÓN

Caso paramétrico. Ejemplo 2 Se ha puesto de manifiesto que cuando las personas se sienten molestas ante la presencia de estímulos ambientales adversos incrementan su comportamiento agresivo. Berkowitz y Frodi (1979) realizaron un experimento para estudiar si el comportamiento agresivo depende no sólo de la presencia de estímulos ambientales adversos sino también del atractivo físico de la persona que supuestamente va a recibir la agresión.

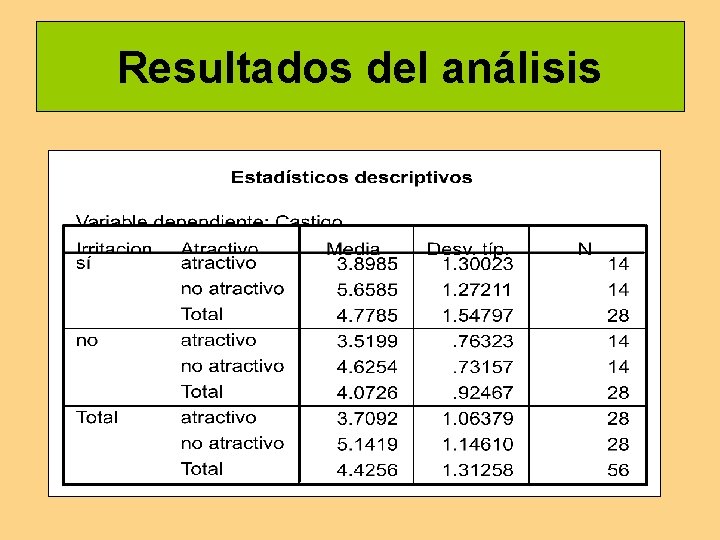
Procedimiento Se seleccionó una muestra de 56 mujeres y se formaron 4 grupos al azar. En el laboratorio, se informó a los sujetos que iban a participar en un estudio sobre la dinámica paterno-filial. Así, en un primer momento, sólo la mitad de las participantes interactuaron con un cómplice del experimentador (que ejercía el rol de padre), entrenado para provocarles irritación. En un segundo momento, a todas se les pasó un vídeo en que una niña (que ejercía el rol filial) realizaba una tarea.

Sigue… En esta segunda parte, para la mitad de las participantes el vídeo mostraba una niña con un aspecto físico atractivo y para la otra mitad la niña tenía un aspecto físico poco atractivo. Durante la presentación del vídeo las participantes debían corregir los errores que la niña cometía en la tarea mediante un estímulo auditivo que podía variar de 1 a 10 en una escala de intensidad.

Resultados del análisis

Prueba de homogeneidad

ANOVA

Ventajas del diseño factorial Se ha descrito, a lo largo de ese tema, los conceptos básicos del diseño factorial o estructura donde se manipulan, dentro de una misma situación experimental, dos o más variables independientes (o factores). En aras a una mejor exposición del modelo se ha descrito, básicamente, el diseño bifactorial a dos niveles, dentro del contexto de grupos completamente al azar. . . //. .

La disposición bifactorial aporta información no sólo de cada factor (efectos principales), sino de su acción combinada (efecto de interacción o efecto secundario). De esta forma, con la misma cantidad de sujetos requerida para experimentos de una sola variable independiente o factor, el investigador puede estudiar simultáneamente la acción de dos o más variables manipuladas. . . //. .

Ello supone un enorme ahorro de tiempo y esfuerzo. Si se tiene en cuenta la posibilidad de analizar la acción conjunto o cruzada de las variables, se concluye que el diseño factorial es una de las mejores herramientas de trabajo del ámbito psicológico, puesto que la conducta es función de muchos factores que actúan simultáneamente sobre el individuo. . . //. .

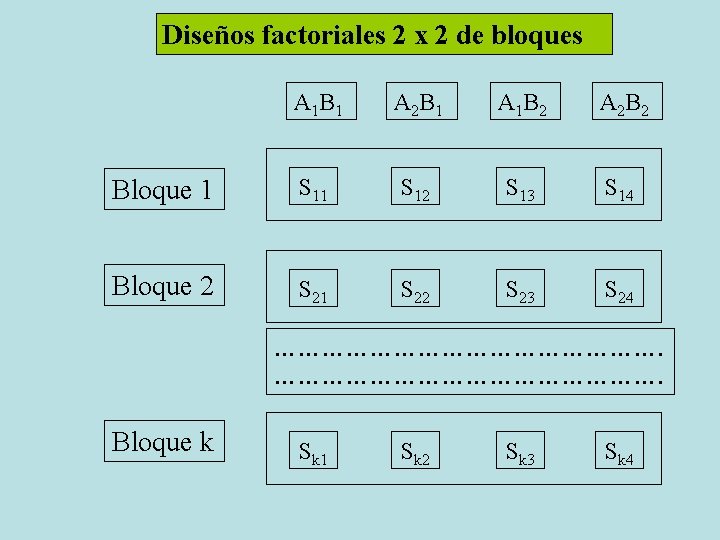
Diseños factoriales 2 x 2 de bloques A 1 B 1 A 2 B 1 A 1 B 2 A 2 B 2 Bloque 1 S 12 S 13 S 14 Bloque 2 S 21 S 22 S 23 S 24 …………………………………………. Bloque k Sk 1 Sk 2 Sk 3 Sk 4

TEMA VIII

ESQUEMA GENERAL Definición general Clasificación Diseño de medidas repetidas simple. Modelo estructural y componentes de variación Diseño de medidas repetidas de Cuadrado Latino. Modelo estructural y componentes de variación Diseño de medidas repetidas factorial. Modelo estructural y componentes de variación DISEÑOS DE MEDIDAS REPETIDAS

Diseño de medidas repetidas El diseño de medidas repetidas es una extensión del diseño de bloques, en que el sujeto sustituye al bloque y actúa de control propio. Con este formato, los sujetos de la muestra reciben todos los tratamientos y repiten medidas o registros de respuesta; asimismo, la comparación de los tratamientos es intra-sujeto. . . //. .

De este modo, el uso del procedimiento de medidas repetidas proporciona un control más efectivo de las fuentes de variación extrañas asociadas, por lo general, a las características individuales; es decir, se consigue una reducción de la variancia del error. . . //. .

Esto es así porque, al actuar el sujeto de bloque, la variabilidad debida a las diferencias individuales es eliminada del error. De este modo, el diseño de medidas repetidas una estructura más potente que los diseños completamente aleatorizados.

Efectos de orden Los efectos de orden (order effects) se derivan de la propia estructura del diseño de medidas repetidas, y deben ser neutralizados para que confundan los efectos de los tratamientos.

Tipos de efectos de orden A) Efecto de período (period effect) B) Efecto residual (carry-over effect)

Efecto de período Los efectos de período ocurren cuando, independientemente del tratamiento aplicado, el sujeto responde al período o posición que, en la secuencia, ocupa el tratamiento (período de administración). Cabe, por lo tanto, la posibilidad de que el sujeto responda mejor al período que al tratamiento en sí mismo. Cuando esto ocurre, el efecto de período confunde la acción del tratamiento.

Efecto residual El efecto residual, conocido por error progresivo, se caracteriza por la persistencia de la acción de un tratamiento más allá del período o tiempo de aplicación. Representa tanto la progresiva acumulación tanto de los efectos facilitadores de la respuesta (efecto de la práctica, aprendizaje, etc. ) como de los efectos obstaculizadores (como la fatiga mental, cansancio físico, etc. ). . . //. .

Cuando, como es frecuente en esos casos, se produce una persistencia del efecto del tratamiento anterior sobre el tratamiento siguiente, se corre el riesgo de que los efectos queden contaminados.

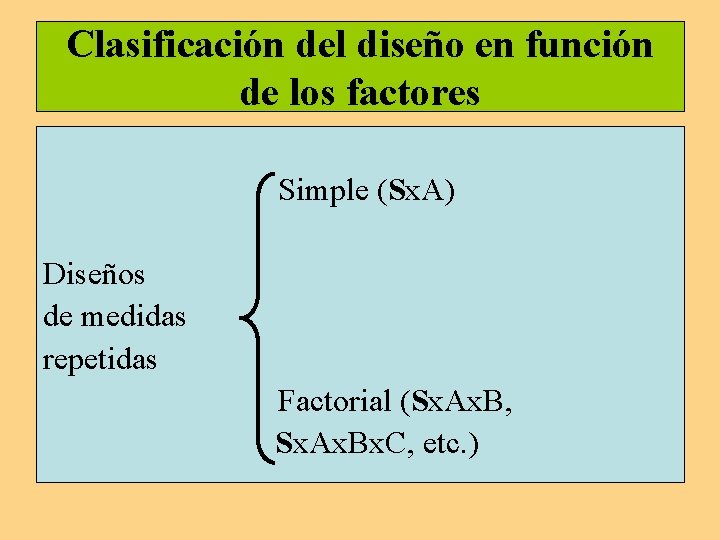
Clasificación del diseño en función de los factores Simple (Sx. A) Diseños de medidas repetidas Factorial (Sx. Ax. B, Sx. Ax. Bx. C, etc. )

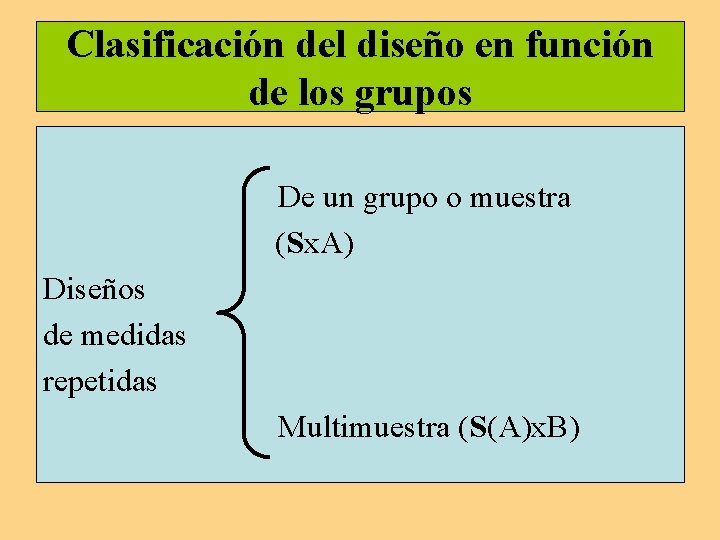
Clasificación del diseño en función de los grupos De un grupo o muestra (Sx. A) Diseños de medidas repetidas Multimuestra (S(A)x. B)

Diseño de medidas repetidas simple de un grupo

Concepto El diseño simple de medidas repetidas es prototípico en esa clase de experimentos, al incorporar la estrategia de comparación intrasujeto. Lindquist (1953) se refiere a estas estructuras como diseños de Tratamientos x Sujetos, ya que los sujetos se cruzan o combinan con los tratamientos. Así mismo, es un diseño simple o unifactorial porque sólo se evalúa la acción de una variable independiente o de tratamientos. . . //. .

La principal ventaja del diseño, dada su especial disposición, es la posibilidad de extraer del error una de sus fuentes de variación más importante: la variación atribuida a las diferencias individuales.

Estructura del diseño La estructura el diseño de medidas repetidas simple es similar al formato factorial de dos variables independientes. A diferencia del diseño factorial, la variable de sujetos no es manipulada ya que se trata de un pseudo-factor. La variable de tratamientos está manipulada por del experimentador y es considerada como un auténtico factor. . . //. .

Supóngase, por ejemplo, que la variable sujetos, simbolizada por S, actúa a n valores, y que el factor A -variable de tratamiento-, a a valores que son aplicados, de forma secuencial, a los sujetos de la muestra. Nótese la similitud entre este diseño y el diseño bifactorial dado que, analíticamente, la variable de sujetos actúa como si fuera un factor. La diferencia estriba sólo en la naturaleza y objetivo de las dos variables. . . //. .

La variable S representa la variabilidad entre sujetos y no es, por lo tanto, un factor manipulado sino de control. La variable A es una dimensión de variación manipulada por el investigador. El propósito del experimento sigue siendo el análisis del posible impacto de la variable de tratamiento sobre la variable de respuesta. . . //. .

Con este formato, no sólo se controlan las diferencias individuales, por el pseudo-factor de sujetos, sino que se minimiza la variancia del error al sustraer una de sus principales fuentes. . . //. .

Así, el diseño de medidas repetidas simple es el procedimiento más eficaz para probar el efecto del tratamiento. Al controlar las diferencias interindividuales, este diseño es, también, un potente procedimiento de análisis, porque al reducir el error se aumenta la precisión y efectividad en probar los efectos de la variable de tratamiento.

Formato del diseño de medidas repetidas. Diseño de medidas repetidas simple, S x A. A 1 Tratamientos A 2 A 3 … Aj Medias Sujetos S 1 Y 12 Y 13 … Y 1 j Y 1. S 2 Y 21 Y 22 Y 23 … Y 2 j Y 2. . Sn ……………………………… . . . Yn 1 Medias Y. 1 Yn 2 Yn 3 … Ynj Y n. Y. 2 Y. j Y. 3 …

Caso paramétrico. Ejemplo 1 Sea, al nivel ilustrativo, la siguiente situación experimental. Se pretende estudiar el efecto de la frecuencia de tres tonos auditivos, o variable A, de igual intensidad (65 db). Para ello, se decide registrar los tiempos de reacción, en milésimas de segundos, a la presentación de los tonos. De la variable independiente frecuencia de tono-, se eligen tres valores: 300 cps. (condición A 1), 600 cps. (condición A 2) y 1200 cps. (condición A 3).

Modelo de prueba de hipótesis Paso 1. Se asume, por hipótesis de nulidad, que los efectos de los tratamientos son nulos. Es decir, H 0: μ 1 = μ 2 = μ 3

Paso 2. Según la hipótesis experimental o hipótesis de efectividad se asume que, uno o más tratamientos o efectos es significativo (distinto de cero). En términos estadísticos se afirma que: H 1: μ 1 μ 2, o μ 1 μ 3, o μ 2 μ 3 H 1: por lo menos una desigualdad

Paso 3. Se asume un modelo ANOVA de aditividad. El estadístico de la prueba es la F normal, a un nivel de significación de α = 0. 05. El tamaño de la muestra experimental es N = n = 3. Paso 4. El cálculo del valor empírico de F se realiza a partir de la correspondiente matriz de datos, una vez ejecutado el experimento.

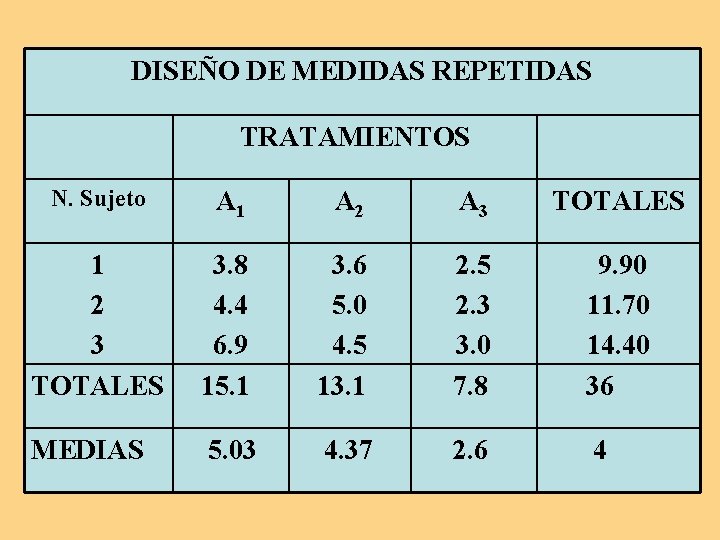
DISEÑO DE MEDIDAS REPETIDAS TRATAMIENTOS N. Sujeto A 1 A 2 A 3 TOTALES 1 2 3 TOTALES 3. 8 4. 4 6. 9 15. 1 3. 6 5. 0 4. 5 13. 1 2. 5 2. 3 3. 0 7. 8 9. 90 11. 70 14. 40 36 MEDIAS 5. 03 4. 37 2. 6 4

ANOVA de medidas repetidas

MODELO ESTRUCTURAL MODELO ADITIVO

Descripción y supuestos Yij = la puntuación del i sujeto bajo la j condición experimental o tratamiento μ = la media global de todos los datos del experimento ηi = μi – μ = el efecto asociado al iésimo sujeto αj = μj – μ = el efecto de jésimo nivel de la variable de tratamiento A ε= i ij el error experimental asociado al sujeto bajo el j tratamiento

Asimismo, para que el modelo sea válido, se asume que: a) ηi NID(0, ση²) b) εij NID(0, σε²) c) Σ = ση² 11' + σε²I

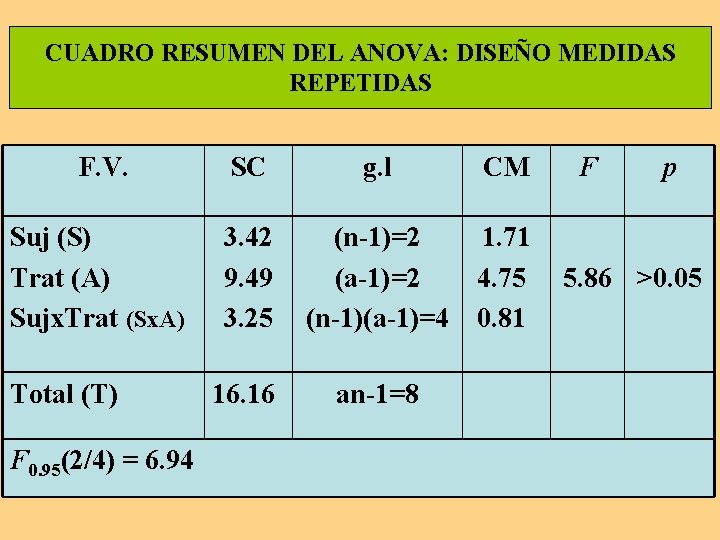
CUADRO RESUMEN DEL ANOVA: DISEÑO MEDIDAS REPETIDAS F. V. SC Suj (S) Trat (A) Sujx. Trat (Sx. A) 3. 42 9. 49 3. 25 Total (T) F 0. 95(2/4) = 6. 94 16. 16 g. l CM (n-1)=2 1. 71 (a-1)=2 4. 75 (n-1)(a-1)=4 0. 81 an-1=8 F p 5. 86 >0. 05

Modelo de prueba de hipótesis Paso 5. Dado que el valor empírico de F es menor que el teórico, se acepta la hipótesis de nulidad relativa a la variable de sujetos y a la de tratamiento, a un nivel del riesgo del cinco por ciento.

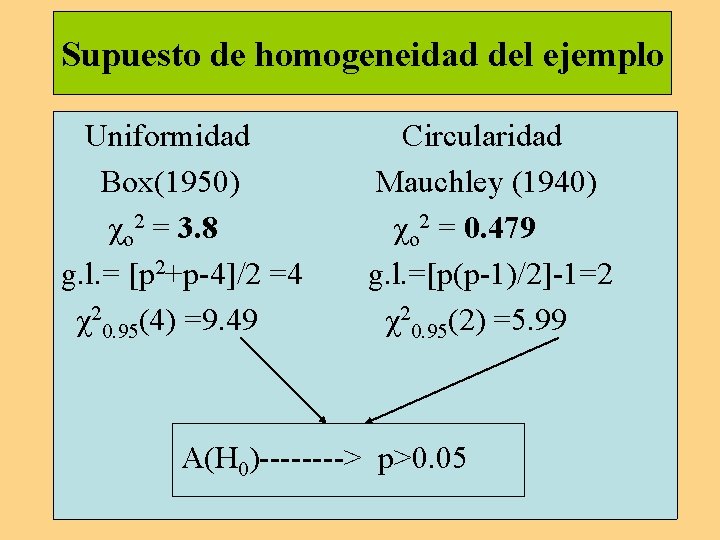
Supuesto de uniformidad o simetría compuesta Según esta restricción, conocida por condición de uniformidad o simetría compuesta, se asume una variancia común para las distintas medidas repetidas y una covariancia común para los diferentes pares de medidas (prueba de Box (1950)).

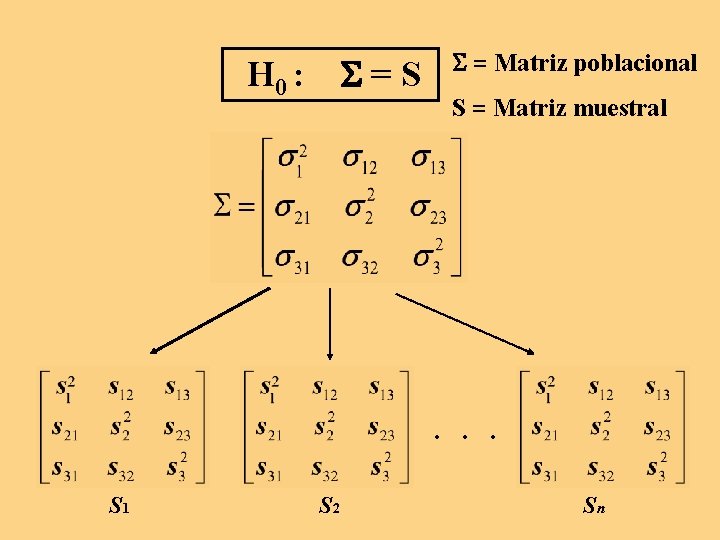
=S H 0 : = Matriz poblacional S = Matriz muestral . . . S 1 S 2 Sn

Prueba de ajuste Prueba de simetría combinada (Box, 1950) H 0: S = Σ

Decisión estadística Se calcula el valor del estadístico B con distribución aproximada a chi-cuadrado y con [a² + a - 4]/2 grados de libertad: B = (1 - C)M = (1 - 075)(15. 2) = 3. 8 y [3² + 3 - 4]/2 = 4 g. l.

El valor teórico de chi-cuadrado es χ0. 95 (4) = 9. 49 Puesto que este valor es mayor que el valor empírico calculado, 3. 8 < 9. 49, se infiere la aceptación de la hipótesis de nulidad y, por tanto, que la matriz de variancia y covariancia muestral se ajusta al patrón específico asumido en la población.

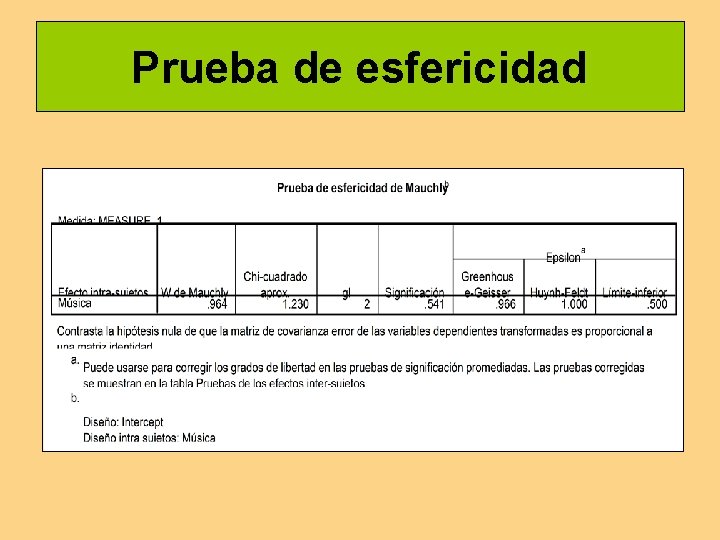
Supuesto de esfericidad Huynh y Feldt (1970) y Rouanet y Lepine (1970) han mostrado que es suficiente el cumplimento de una condición más débil o condición de esfericidad (circularidad). Esta condición sólo requiere que las variancias de las diferencias entre todos los pares de medidas repetidas sean iguales (prueba de esfericidad de Mauchley (1940))

Supuesto de homogeneidad del ejemplo Uniformidad Box(1950) χo 2 = 3. 8 g. l. = [p 2+p-4]/2 =4 χ20. 95(4) =9. 49 Circularidad Mauchley (1940) χo 2 = 0. 479 g. l. =[p(p-1)/2]-1=2 χ20. 95(2) =5. 99 A(H 0)----> p>0. 05

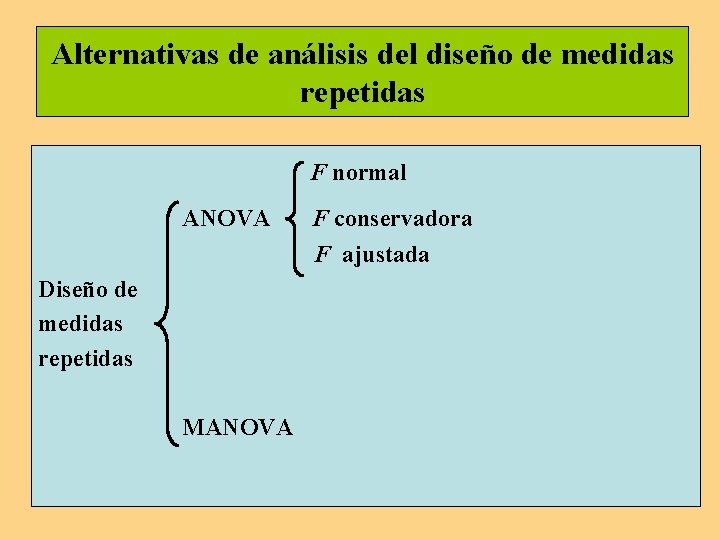
Alternativas de análisis del diseño de medidas repetidas F normal ANOVA F conservadora F ajustada Diseño de medidas repetidas MANOVA

Fórmulas para el cálculo de los grados de libertad de las F's.

Grados de libertad de F F normal F conservadora F ajustada Numerador (a-1) 1 (a-1) Denominador (n-1)(a-1) n-1 (n-1)(a-1)

Factores de ajuste Epsilón de: Greenhouse y Geisser (1959) Huynh y Feldt (1970)

Épsilon de Greeenhouse y Geisser (1959). = 0. 72

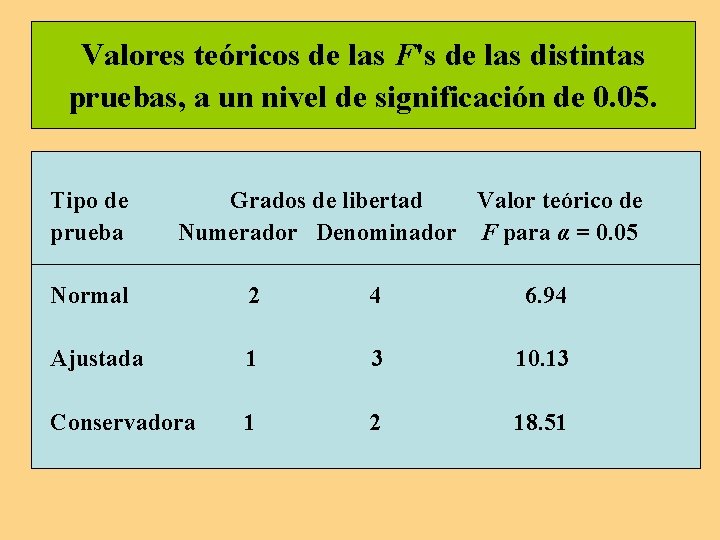
Valores teóricos de las F's de las distintas pruebas, a un nivel de significación de 0. 05. Tipo de prueba Grados de libertad Valor teórico de Numerador Denominador F para α = 0. 05 Normal 2 4 6. 94 Ajustada 1 3 10. 13 Conservadora 1 2 18. 51

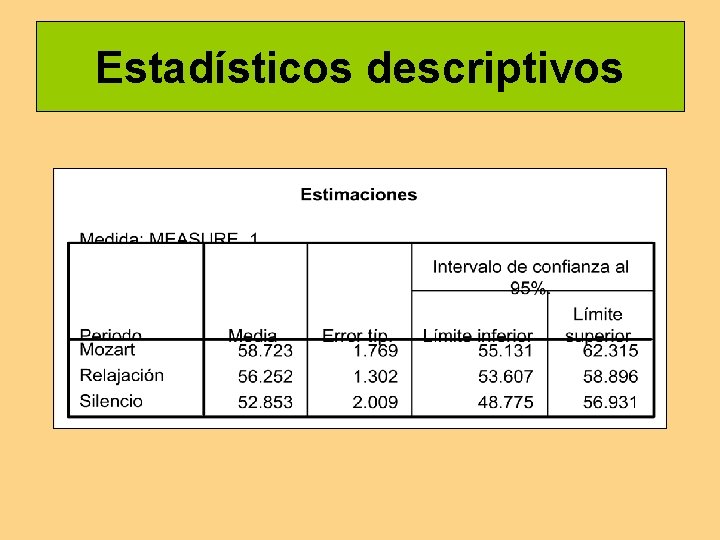
Caso paramétrico. Ejemplo 2 Rauscher, Show y Ky (1993) estudiaron si la audición de la sonata K 488 de Mozart incrementaba el rendimiento en tareas cognitivas. Se pidió a un total de 36 estudiantes que ejecutaran tres tareas de razonamiento espacial. Previo a las tareas los sujetos escuchaban, por un periodo de diez minutos, una de las siguientes piezas: (a) la sonata para dos pianos K 488 de Mozart, (b) música de relajación y (c) silencio. Los efectos de orden se controlaron mediante contrabalanceo entresujetos de las tres audiciones. La variable dependiente fue la puntuación obtenida en la tarea de razonamiento espacial.

Estadísticos descriptivos

Prueba de esfericidad

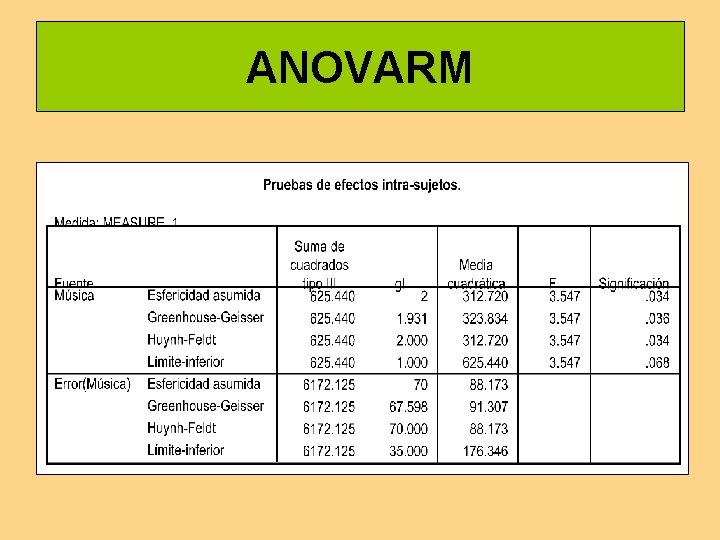
ANOVARM

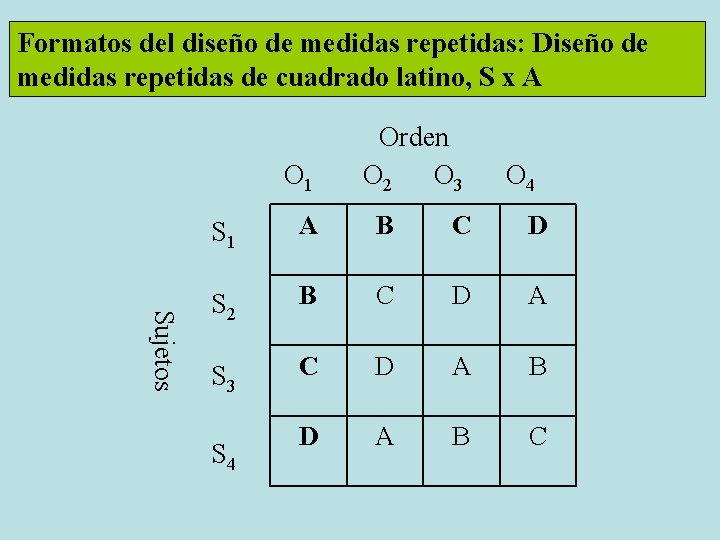
Formatos del diseño de medidas repetidas: Diseño de medidas repetidas de cuadrado latino, S x A O 1 Orden O 2 O 3 O 4 Sujetos S 1 A B C D S 2 B C D A S 3 C D A B C S 4

Formatos del diseño de medidas repetidas: Diseño de medidas repetidas factorial, S x A x B. Tratamientos A 1 … A 2 Aj … B 1 … Bk Medias B 1 … Bk S 1 Y 111. . Y 11 k Y 121. . Y 12 k … Y 1 j 1. . Y 1 jk Y 1. . Sujetos S 2 Y 211. . Y 22 k Y 221. . Y 22 k … Y 2 j 1. . Y 2 jk . …………………………………………… Sn Yn 11. . Yn 1 k Medias Y. 11. . Y. 12 Y 2. . . … Ynj 1. . Ynjk Yn. . Y. 21. . Y. 2 k … Y. j 1. . Y. jk Y… Yn 21. . Yn 2 k

TEMA IX

ESQUEMA GENERAL Definición general Clasificación Diseño factorial mixto con una variable entre y otra intra. Modelo estructural y componentes de variación Diseño split-plot Comparación de las fuentes de variación del Diseño mixto con el de medidas repetidas simple y el completamente al azar DISEÑOS FACTORIALES MIXTOS

Diseño de medidas repetidas multigrupo o factorial mixto

Diseño de medidas repetidas multigrupo El diseño de medidas repetidas multigrupo, conocido también por diseño factorial mixto, incorpora dos estrategias de inferencia de hipótesis: estrategia de comparación entre grupos y estrategia de comparación intra sujetos. La estructura mixta combina, en un mismo experimento, el procedimiento de grupos independientes y el procedimiento con sujetos de control propio. . . //. .

Puesto que el diseño mixto integra, en un mismo estudio, dos enfoques de investigación se aplica a aquellas situaciones donde están presentes, por lo menos, dos variables independientes. Así, los valores o niveles de la primera variable independiente genera grupos separados y su efecto se infiere por la comparación entre grupos o entre sujetos. . . //. .

Esta variable independiente es conocida como variable entre. Los valores de la segunda variable se administran a todos los sujetos, en cuyo caso los sujetos repiten medidas. Dado el carácter de repetición, esa segunda variable recibe el nombre de variable intra. De esto se concluye que el diseño mixto requiere siempre una estructura factorial. O sea, son experimentos donde intervienen como mínimo dos variables.

Clasificación

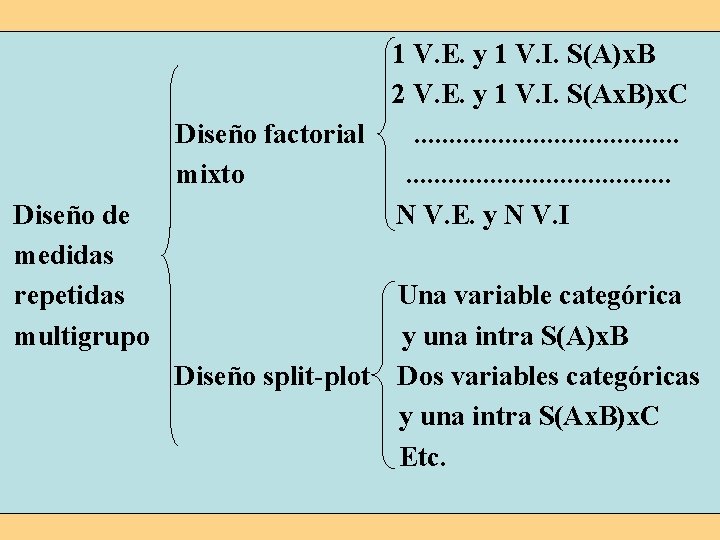
Diseño de medidas repetidas multigrupo 1 V. E. y 1 V. I. S(A)x. B 2 V. E. y 1 V. I. S(Ax. B)x. C Diseño factorial. . . . . mixto. . . . . N V. E. y N V. I Una variable categórica y una intra S(A)x. B Diseño split-plot Dos variables categóricas y una intra S(Ax. B)x. C Etc.

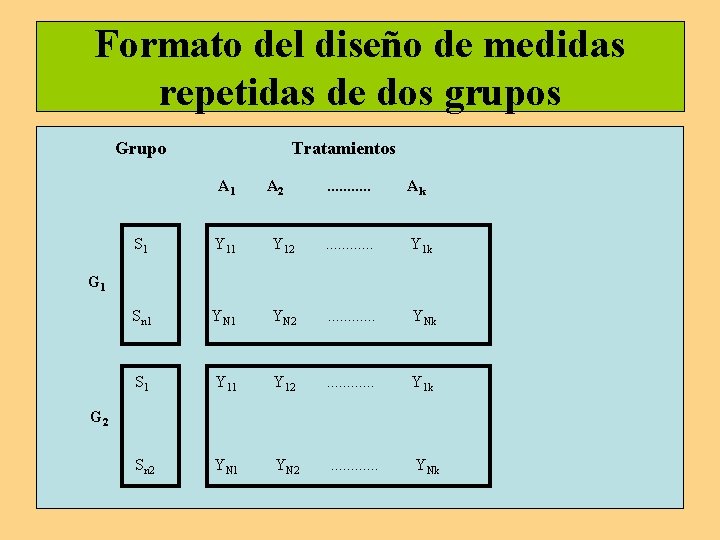
Formato del diseño de medidas repetidas de dos grupos Grupo Tratamientos A 1 A 2 . . . Ak S 1 Y 12 . . . Y 1 k Sn 1 YN 2 . . . YNk S 1 Y 12 . . . Y 1 k Sn 2 YN 1 YN 2 . . . YNk G 1 G 2

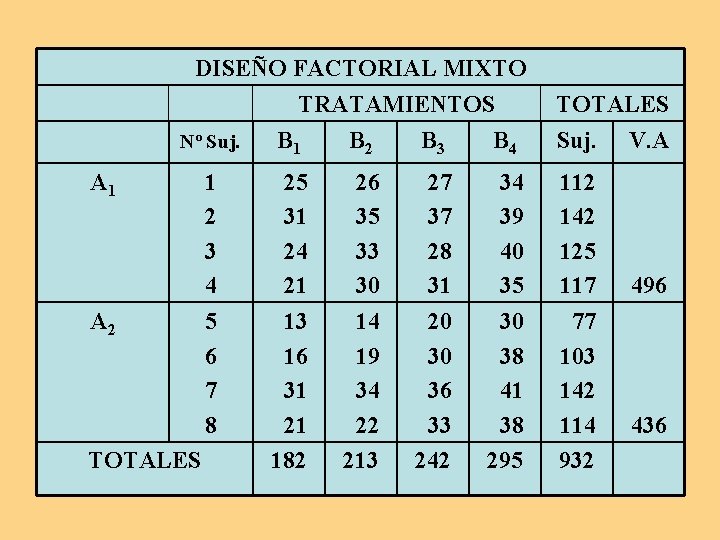
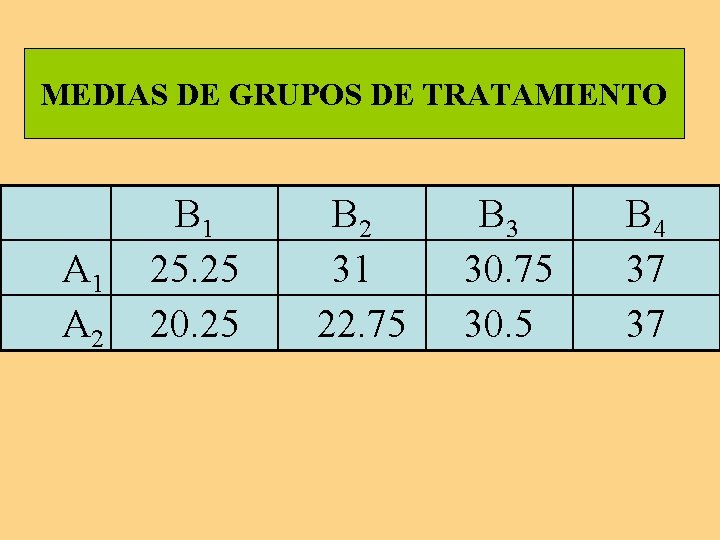
Ejemplo práctico 1 Un experimentador pretende estudiar el efecto que sobre la memoria icónica tienen dos variables: campo pos-exposición y tiempo de presentación. De la primera variable, selecciona dos valores: campo pos-exposición brillante (A 1) y campo pos-exposición oscuro (A 2). De la segunda, elige cuatro valores: B 1 = 45 c/sg, B 2 = 90 c/sg, B 3 = 180 c/sg, y B 4 = 240 c/sg.

Para ejecutar este experimento, confecciona tarjetas donde aparecen letras consonantes, seleccionadas al azar, y las dispone en matrices 3 x 4. La tarea a realizar por los sujetos, va a consistir en identificar, de forma correcta, la máxima cantidad de letras. A su vez, decide que cada sujeto ejecute 40 ensayos (diez tarjetas por tiempo de presentación). La variable dependiente es la cantidad de identificaciones correctas en bloques de 10 ensayos.

Modelo de prueba estadística Paso 1. Formulación de las hipótesis de nulidad: H 0: α 1 = α 2 = 0 H 0: ß 1 = ß 2 = ß 3 = ß 4 = 0 H 0: αß 11 = αß 12 = αß 13 = αß 14 = αß 21 = αß 22 = αß 23 = αß 24 = 0

Paso 2. A cada hipótesis de nulidad está asociada la siguiente hipótesis alternativa: H 1: por lo menos una desigualdad

Paso 3. Se asume el modelo ANOVA lineal. El estadístico de la prueba es la F normal (bajo el supuesto de homogeneidad y simetría), con un nivel de significación de α = 0. 05. El tamaño de la muestra experimental es N = an = 8 y la cantidad de observaciones abn = 32. Paso 4. Se calcula el valor empírico de F a partir de la correspondiente matriz de datos del experimento.

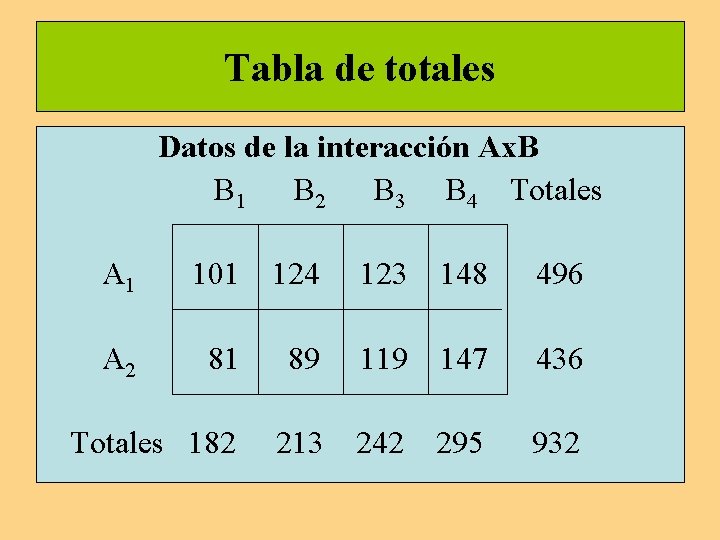
DISEÑO FACTORIAL MIXTO TRATAMIENTOS TOTALES Nº Suj. B 1 B 2 B 3 B 4 Suj. 1 2 3 4 5 6 7 8 25 31 24 21 13 16 31 21 182 26 35 33 30 14 19 34 22 213 27 37 28 31 20 30 36 33 242 34 39 40 35 30 38 41 38 295 112 142 125 117 77 103 142 114 932 A 1 A 2 TOTALES V. A 496 436

Modelo estructural del diseño Yijk = μ + [αj + ηi/j] + [βk + (αβ)jk + (ηβ)ik/j ] + εijk

Supuestos del anova Yij = la puntuación del i sujeto bajo el j valor A y el k valor de B μ = la media común a todos los datos del experimento. αj = es el efecto de j nivel de la variable A. ηi/j = el efecto asociado al i sujeto dentro de j nivel de A. ßk = el efecto del k nivel de B. (αß)jk = el efecto de la interacción de Aj y Bk. (ηß)ik/j = el efecto de la interacción de Si y Bk, intra Aj. εijk = el error de medida.

Dado que sólo hay un dato por casilla –combinación de S, A y B–, no hay variabilidad intra-casilla, Así, Sx. B/A estima la variancia del error. Se asume que: a) ηi NID(0, ση²) b) (ηß)ik/j NID(0, σηß²) b) εijk NID(0, σε²)

Resumen de las fuentes de variación del diseño factorial mixto Entre sujetos Variable A Sujetos intra A Intra sujetos Variable B Interacción A x B Sujetos x B intra A

Tabla de totales Datos de la interacción Ax. B B 1 B 2 B 3 B 4 Totales A 1 101 124 123 148 496 A 2 81 89 119 147 436 Totales 182 213 242 295 932

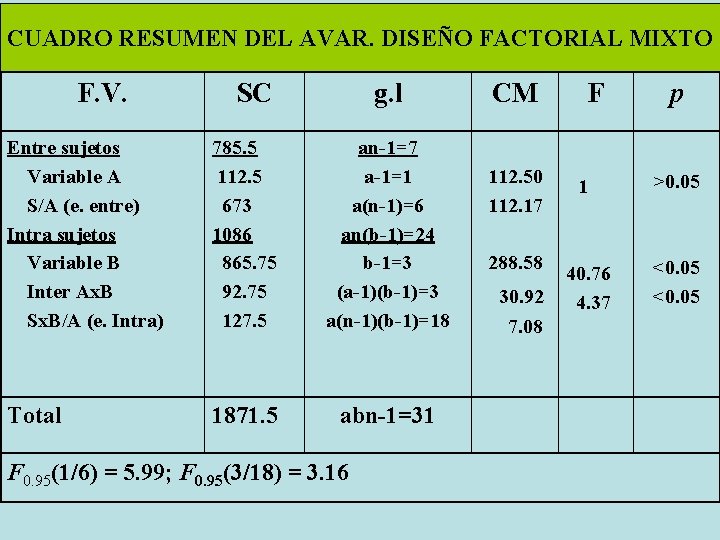
CUADRO RESUMEN DEL AVAR. DISEÑO FACTORIAL MIXTO F. V. SC g. l Entre sujetos Variable A S/A (e. entre) Intra sujetos Variable B Inter Ax. B Sx. B/A (e. Intra) 785. 5 112. 5 673 1086 865. 75 92. 75 127. 5 an-1=7 a-1=1 a(n-1)=6 an(b-1)=24 b-1=3 (a-1)(b-1)=3 a(n-1)(b-1)=18 Total 1871. 5 abn-1=31 F 0. 95(1/6) = 5. 99; F 0. 95(3/18) = 3. 16 CM 112. 50 112. 17 288. 58 30. 92 7. 08 F p 1 >0. 05 40. 76 4. 37 <0. 05

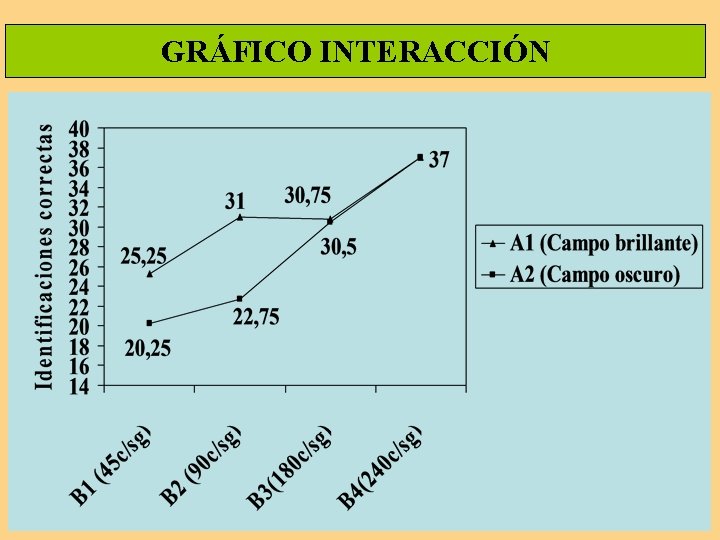
Modelo de prueba estadística Paso 5. De los resultados del análisis, se infiere la aceptación de la hipótesis de nulidad para la variable A y su no-aceptación para la variable B y la interacción Ax. B, con una probabilidad de error del 5 por ciento.

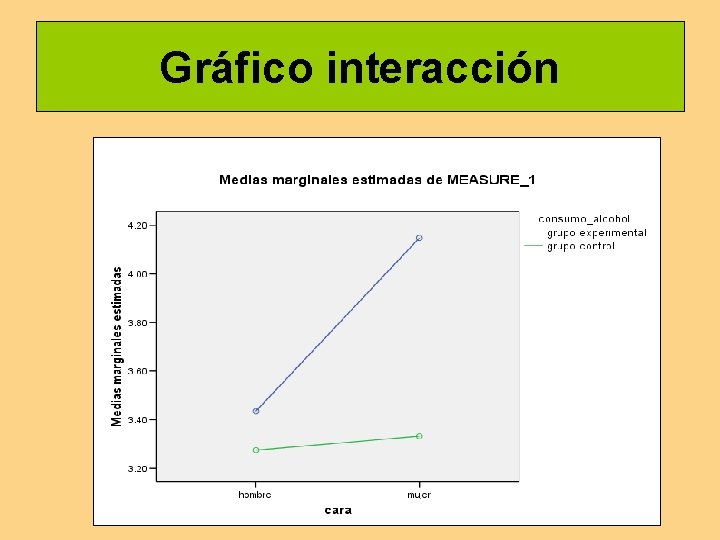
MEDIAS DE GRUPOS DE TRATAMIENTO A 1 A 2 B 1 25. 25 20. 25 B 2 31 22. 75 B 3 30. 75 30. 5 B 4 37 37

GRÁFICO INTERACCIÓN

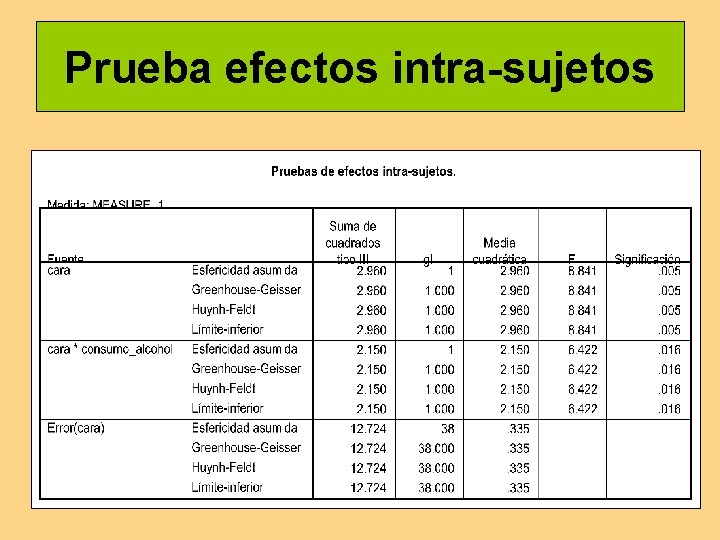
Ejemplo práctico 2 Jones et al. (2003) estudiaron el efecto que tiene el consumo de alcohol sobre la valoración del atractivo de personas no conocidas. En el experimento, participaron 40 varones a los que se les presentaron caras de hombres y de mujeres y tenían que valorar su atractivo físico en una escala del 1 al 7 (de menor a mayor). Antes de la presentación de los estímulos, la mitad de los participantes ingirió una dosis de alcohol, mientras que la otra mitad ingirió una bebida refrescante. Se trata de un diseño factorial mixto 2 x 2 con una variable intrasujeto (el sexo de la persona cuya cara se ha de valorar) y una variable entresujeto (el consumo de alcohol).

Prueba efectos intra-sujetos

Prueba efectos inter-sujetos

Gráfico interacción

Fin de los diseños experimentales clásicos