Superconducting electronics from Josephson effects to quantum computing



![Thin film preparation methods [R. Wördenweber] Thin film preparation methods [R. Wördenweber]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-4.jpg)
![Serial arrays for voltage standard [wikipedia] Serial arrays for voltage standard [wikipedia]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-8.jpg)
![[ J. Niemeier ] 9 [ J. Niemeier ] 9](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-9.jpg)

![[Gallop] [Gallop]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-11.jpg)


![LIC = 1. 25 Φ 0 k = 0 ↔ k =1 [Ruggiero, Rudman] LIC = 1. 25 Φ 0 k = 0 ↔ k =1 [Ruggiero, Rudman]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-15.jpg)



![Parameter [SQUID Handbook] Parameter [SQUID Handbook]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-21.jpg)
![Transition to films [SQUID Handbook] Transition to films [SQUID Handbook]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-23.jpg)

![HTS-RF-SQUID [FZ Jülich] HTS-RF-SQUID [FZ Jülich]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-25.jpg)










![[Drung] [Drung]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-47.jpg)
![Direct electronics with AFP (additional positive feedback) [Drung] Direct electronics with AFP (additional positive feedback) [Drung]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-48.jpg)

![Wire incoupling structures [ J. Clarke ] Wire incoupling structures [ J. Clarke ]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-52.jpg)
![Multi channel gradiometer [ Biomagnetisches Zentrum der FSU Jena ] Multi channel gradiometer [ Biomagnetisches Zentrum der FSU Jena ]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-53.jpg)





![[Chesca] [Chesca]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-68.jpg)
![Serial SQIF [Schultze] Serial SQIF [Schultze]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-74.jpg)
![2 p. T / √ Hz [IPHT Jena]} 2 p. T / √ Hz [IPHT Jena]}](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-75.jpg)
![2 D- SQIF array [R. Fagaly] 2 D- SQIF array [R. Fagaly]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-76.jpg)
![Bi-SQUID [R. Fagaly] Bi-SQUID [R. Fagaly]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-77.jpg)
- Slides: 77

Superconducting electronics -from Josephson effects to quantum computing -by Pascal Febvre and Paul Seidel

Superconducting electronics – Part 2 Josephson junctions, arrays and SQUIDs

Josephson devices � Mainly thin film technology � Different types (SIS, SNS, SINIS, SFS, …) � Josephson � Complex junctions as active devices (e. g. mixers) superconducting circuits (e. g. RSFQ) � Different sensors (SQUIDs, SQUIFs, radiation detectors) 3
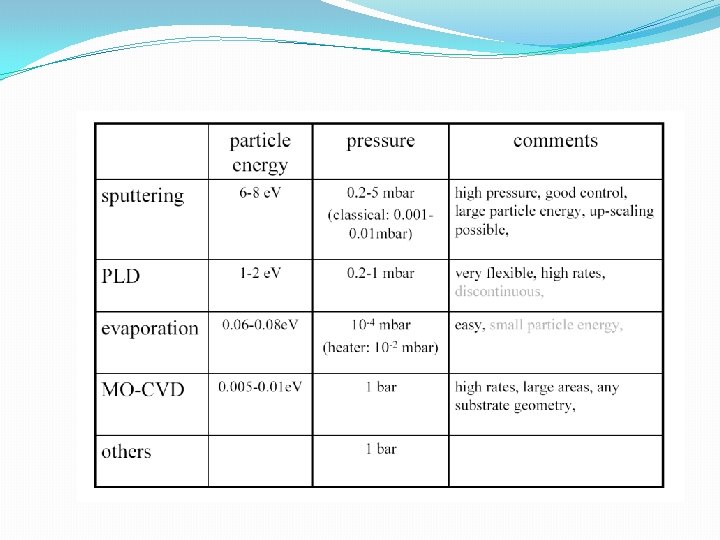
![Thin film preparation methods R Wördenweber Thin film preparation methods [R. Wördenweber]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-4.jpg)
Thin film preparation methods [R. Wördenweber]


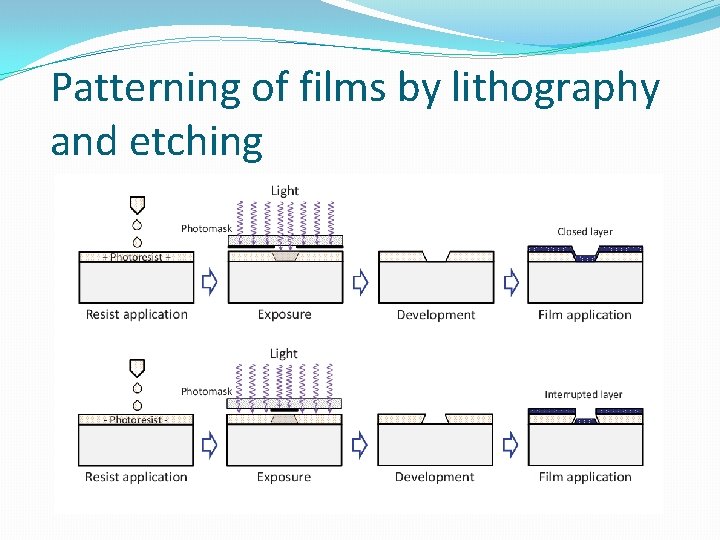
Patterning of films by lithography and etching

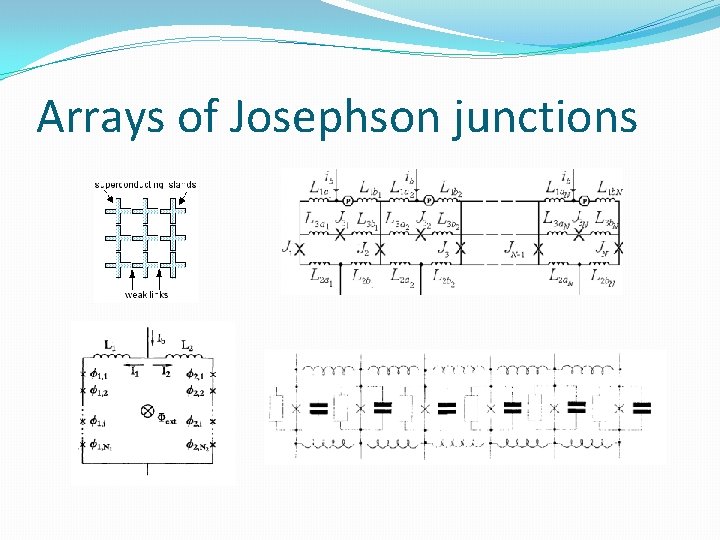
Arrays of Josephson junctions
![Serial arrays for voltage standard wikipedia Serial arrays for voltage standard [wikipedia]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-8.jpg)
Serial arrays for voltage standard [wikipedia]
![J Niemeier 9 [ J. Niemeier ] 9](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-9.jpg)
[ J. Niemeier ] 9

SQUIDs Superconducting quantum interference devices �RF-SQUID �DC-SQUID �(D)ROS-SQUID �Digital SQUIDs �Π-SQUID �Supercond. Quantum interference filter (SQIF)
![Gallop [Gallop]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-11.jpg)
[Gallop]

RF-SQUID �non-linear inductance of Josephson junction gives a periodic modulation of the resonance frequency of the tank circuit �these changes follow the amplitude of the rf current for a given working frequency �response variies with Φ 0 = h/2 e = 2, 07 10 -15 Vs �advantage: no electrical contacts �disadvantage: noise of tank curcuit and amplifier large than intrinsic SQUID noise

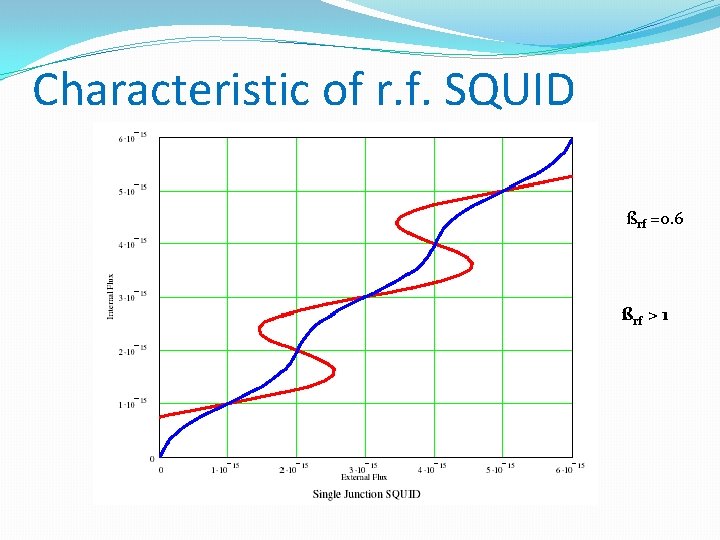
RF-SQUID �Total flux Φ = Φex + LIC sin φ �Phase φ = 2 π Φ / Φ 0 �Φ = Φex + LIC sin (2 π Φ / Φ 0 ) �SQUID-Parameter ßrf = 2 π LIC / Φ 0

Characteristic of r. f. SQUID ßrf =0. 6 ßrf > 1
![LIC 1 25 Φ 0 k 0 k 1 Ruggiero Rudman LIC = 1. 25 Φ 0 k = 0 ↔ k =1 [Ruggiero, Rudman]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-15.jpg)
LIC = 1. 25 Φ 0 k = 0 ↔ k =1 [Ruggiero, Rudman]

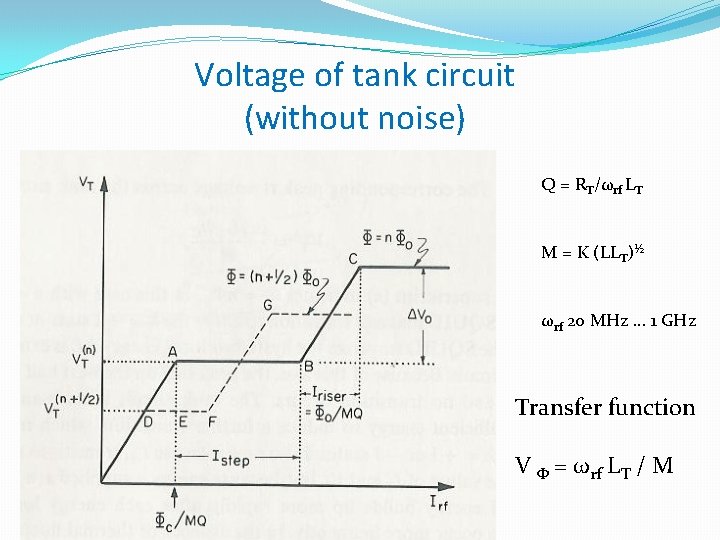
Voltage of tank circuit (without noise) Q = RT/ωrf LT M = K (LLT)½ ωrf 20 MHz … 1 GHz Transfer function V Φ = ωrf LT / M

Transfer function �K can not be choosen too small ! �Irf has to cut the step for all flux values �for LIC ≈ Φ 0 follows K 2 Q ≥ π / 4 (≈ 1) �with K ≈ Q -1/2 results

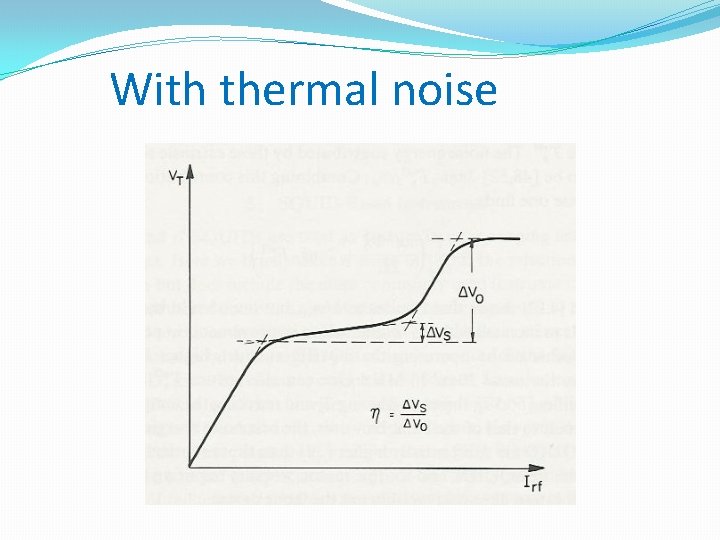
With thermal noise

Noise of RF-SQUIDs �Intrinsic flux noise �Final step slope (thermal noise)

Energy resolution �Amplifier at room temperature and capacitive contributions of current lines result in an effective noise temperature
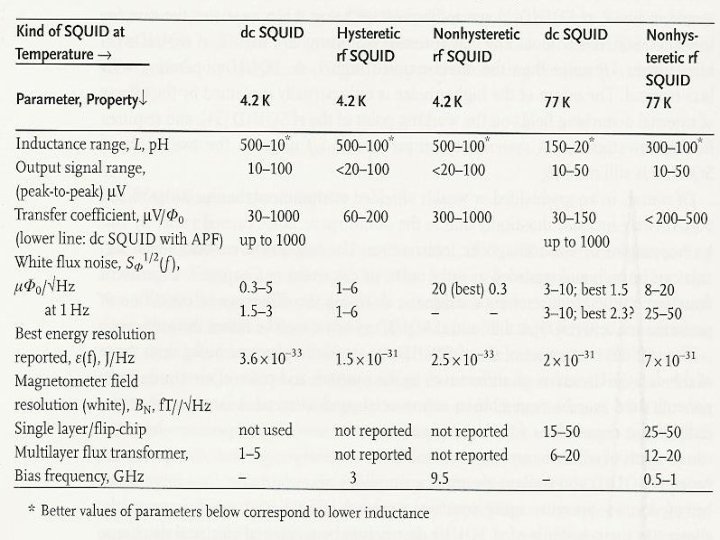
![Parameter SQUID Handbook Parameter [SQUID Handbook]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-21.jpg)
Parameter [SQUID Handbook]

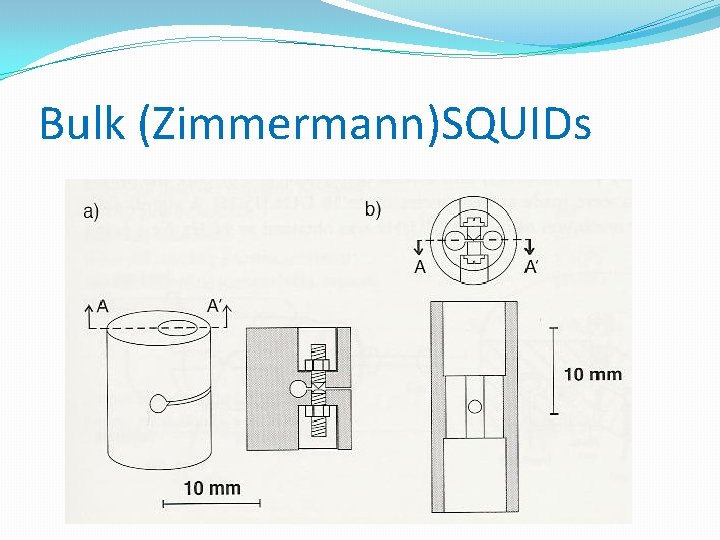
Bulk (Zimmermann)SQUIDs
![Transition to films SQUID Handbook Transition to films [SQUID Handbook]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-23.jpg)
Transition to films [SQUID Handbook]

Zimmermann-SQUID IPTT Tschernogolovka/ FSU Jena about 1970 Niobium bulk Zimmermann-SQUID IPTM Tschernogolovka about 1975 Thin film –bulk hybrid technique [Meyer]
![HTSRFSQUID FZ Jülich HTS-RF-SQUID [FZ Jülich]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-25.jpg)
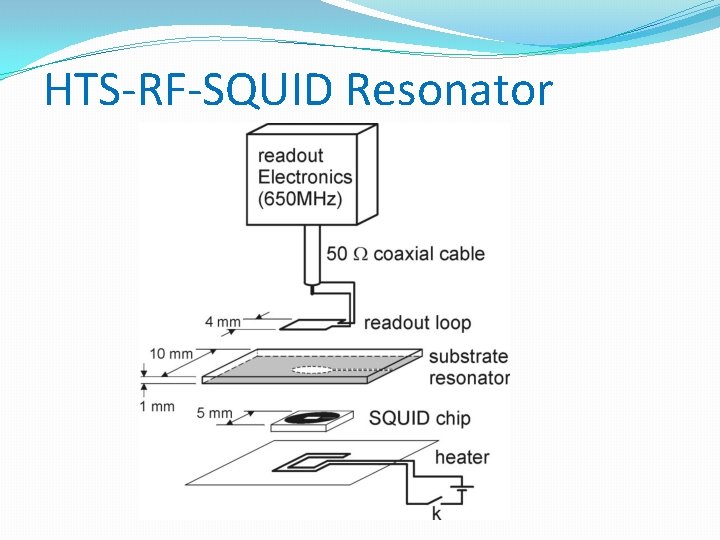
HTS-RF-SQUID [FZ Jülich]

Step-edge junction

HTS-RF-SQUID Resonator

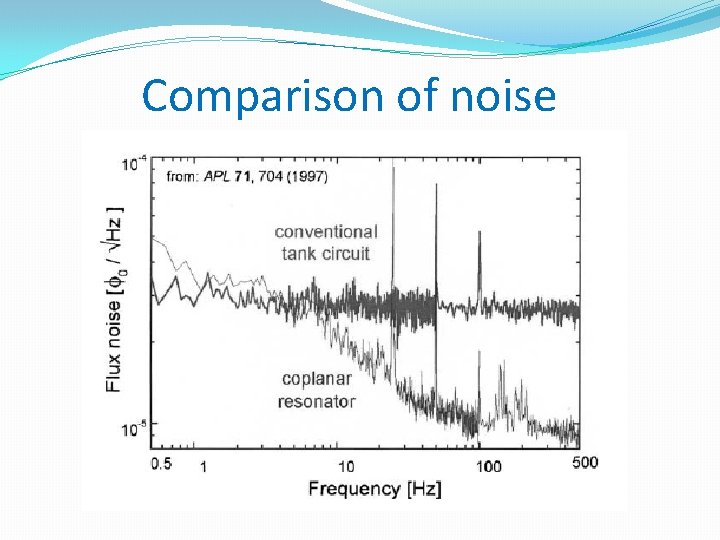
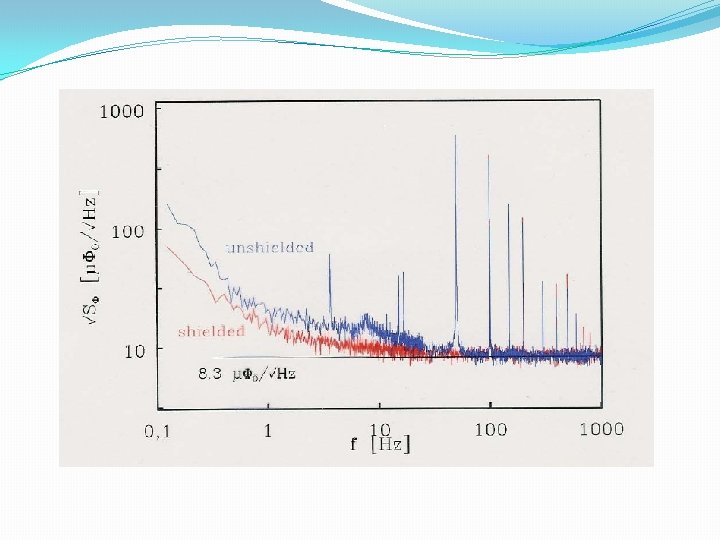
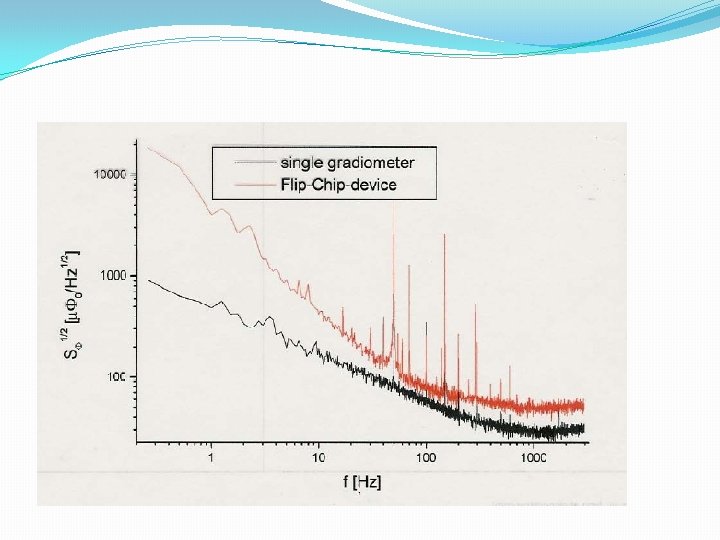
Comparison of noise

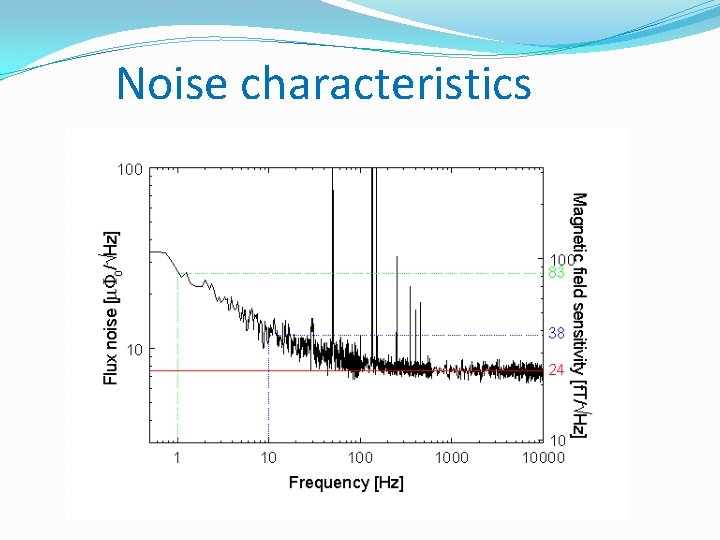
Noise characteristics

Planar microwave SQUID

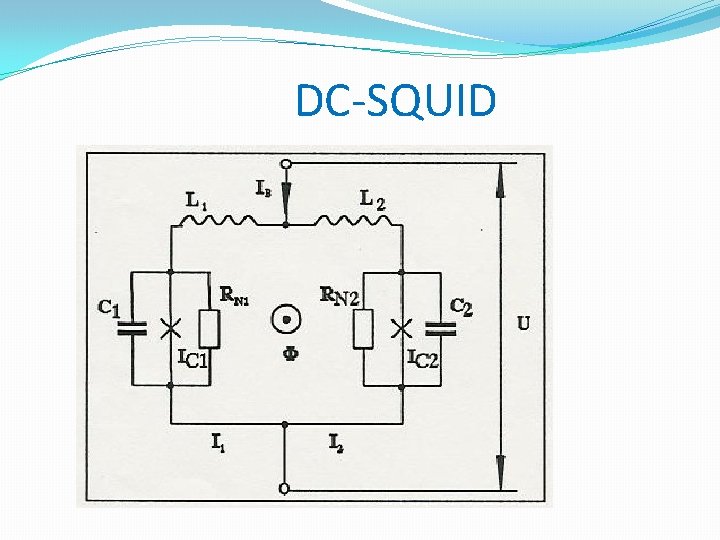
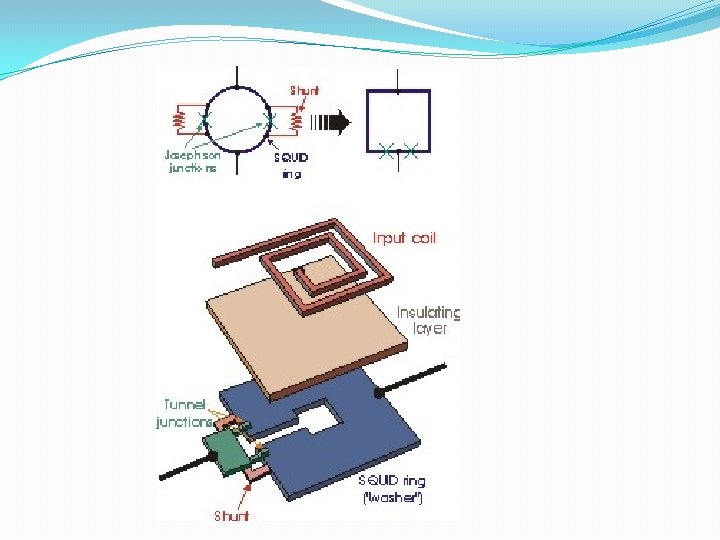
DC-SQUID

Interference of the ring currents �Current splitting �Ring current J → I = I 1 + I 2 I 1 = +J I 2 = � Josephson currents I 1 = Icsinφ1 I 2 = Icsinφ2 -J

1. ) for Ic 1 = Ic 2 = Ic (symmetrical) � Flux is external Flux plus self field by ring current Φ = Φex + LJ � Phase difference is 2π-periodical φ2 – φ1 = 2 π Φ / Φ 0 = 2 π (Φex + LJ) / Φ 0

2. ) Approximation without flux contribution of the ring current ( this current is in general J < Ic thus LJ < LIc → should be << Φ 0 /2, i. e. << 1 Inductance (Ring) Parameter

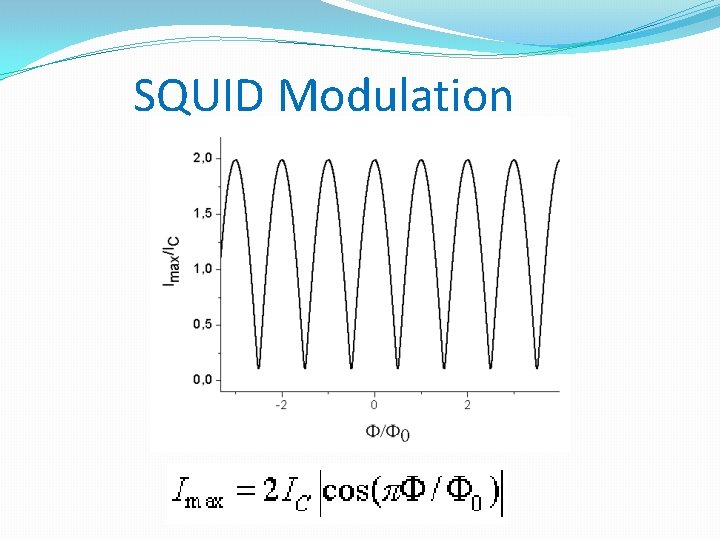
With this assumption it is Φ = Φex and thus follows I = Ic [sinφ1 + sin (φ1 + 2πΦex/Φ 0)] with δ = φ1 + π Φex/Φ 0 and simple transformatios for sin functions results in I = 2 Ic sinδ cos (πΦex /Φ 0)

SQUID Modulation

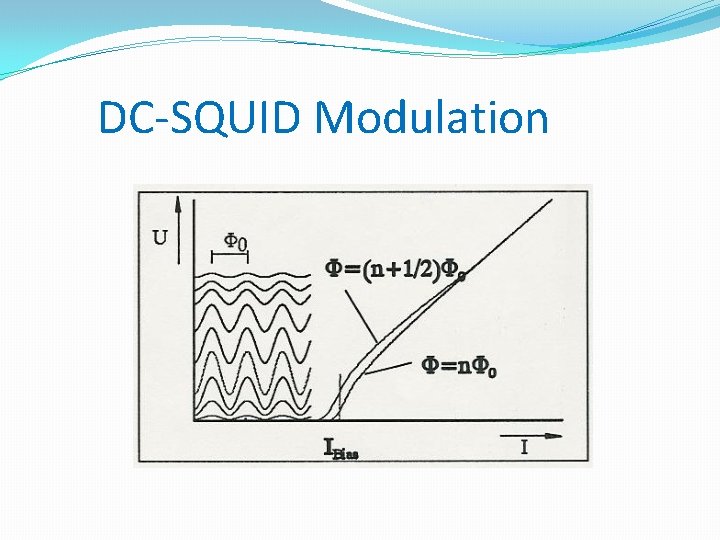
Integer values of flux Φex = n · Φ 0 cos = 1 Maximum value Is, max = 2 Ic obtained Ring current disappears (sinφ1 = sinφ2 = 1)

Half integer values of flux �Φex = (n+1/2) Φ 0, n = 0, ± 1, ± 2, … �Is, max = 0 �Ring current reaches maximum (± Ic)

DC-SQUID Modulation

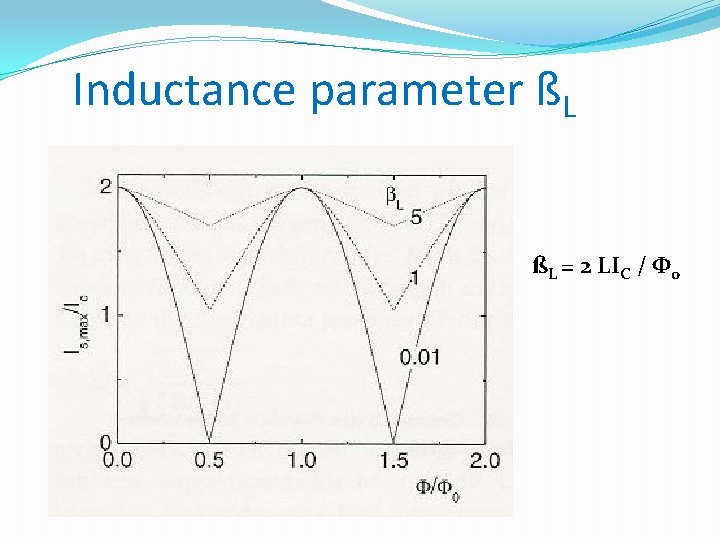
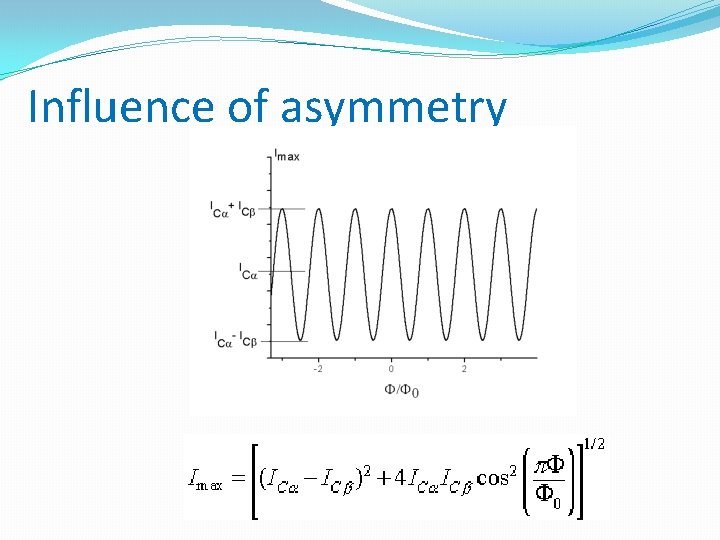
Asymmetric case �Is, max = Ic 1 + Ic 2 �but Is, max (Φ) nearer to the maximum �Modulation amplitude becomes smaller �Dependence on βL �optimum βL~ 1 (Limit for Aeff at fixed L)

Inductance parameter ßL ßL = 2 LIC / Φ 0

Influence of asymmetry

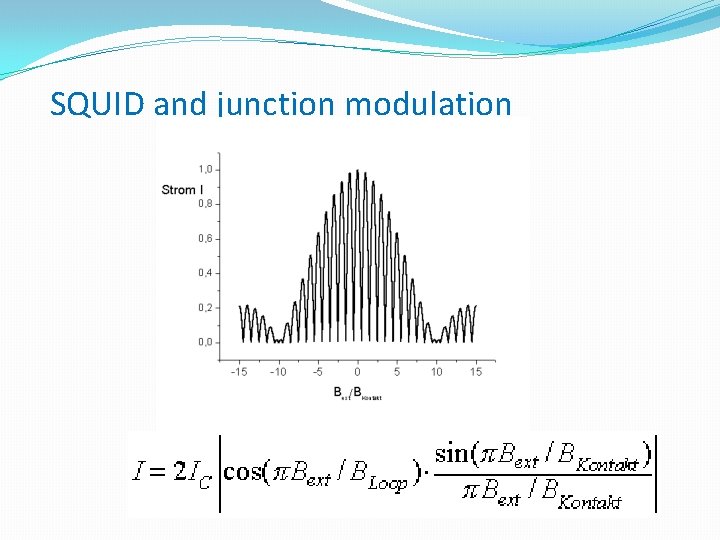
SQUID and junction modulation

Energy resolution

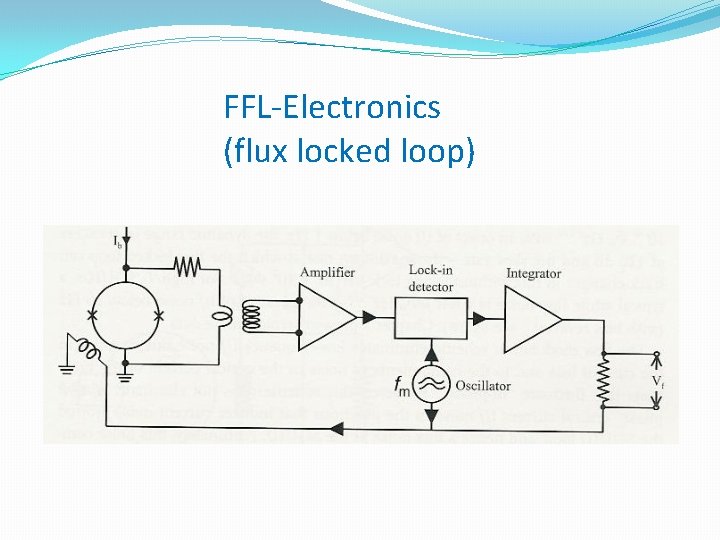
FFL-Electronics (flux locked loop)

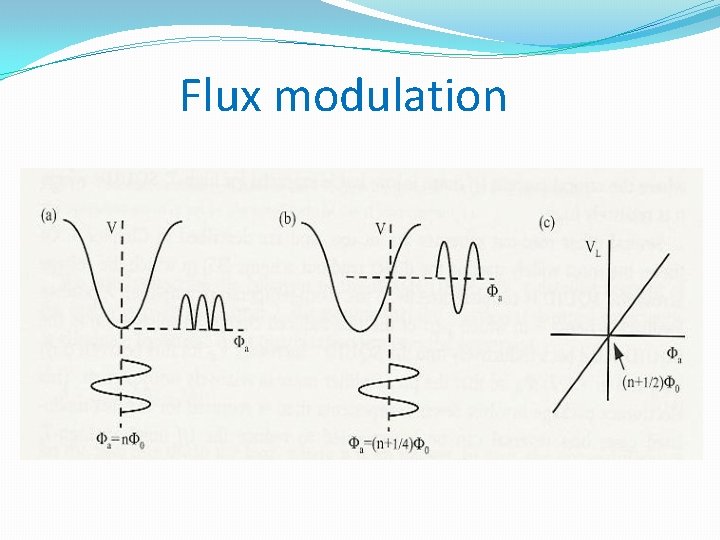
Flux modulation
![Drung [Drung]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-47.jpg)
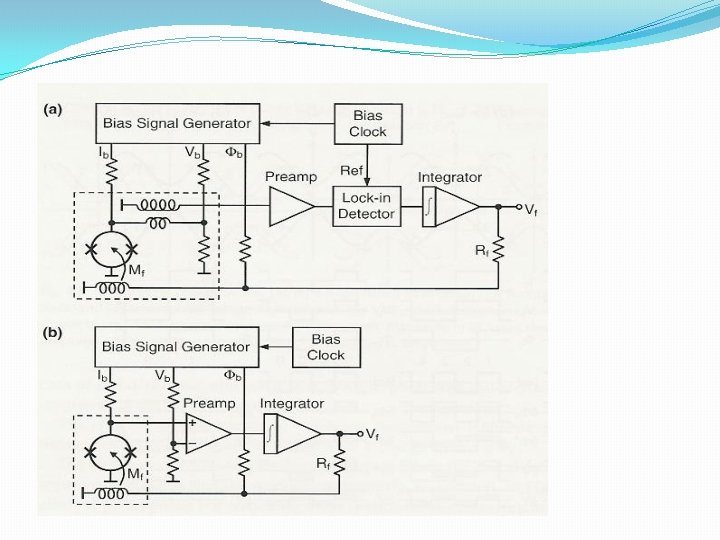
[Drung]
![Direct electronics with AFP additional positive feedback Drung Direct electronics with AFP (additional positive feedback) [Drung]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-48.jpg)
Direct electronics with AFP (additional positive feedback) [Drung]

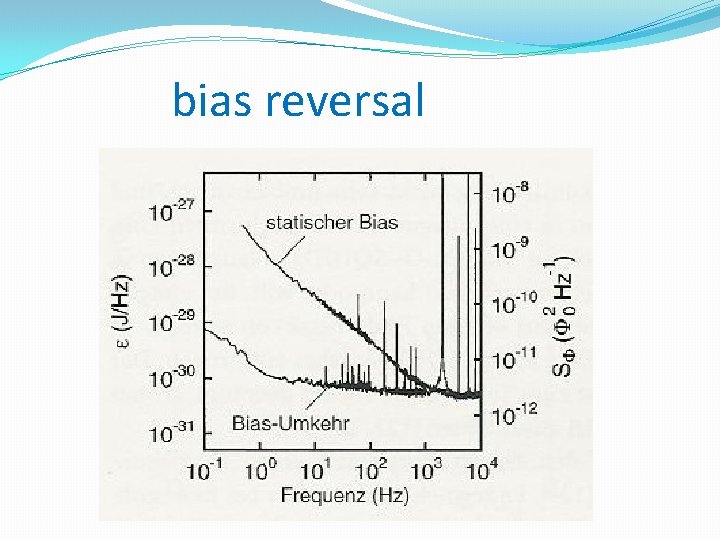
bias reversal


Gradiometer types
![Wire incoupling structures J Clarke Wire incoupling structures [ J. Clarke ]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-52.jpg)
Wire incoupling structures [ J. Clarke ]
![Multi channel gradiometer Biomagnetisches Zentrum der FSU Jena Multi channel gradiometer [ Biomagnetisches Zentrum der FSU Jena ]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-53.jpg)
Multi channel gradiometer [ Biomagnetisches Zentrum der FSU Jena ]


LTS-SQUIDs

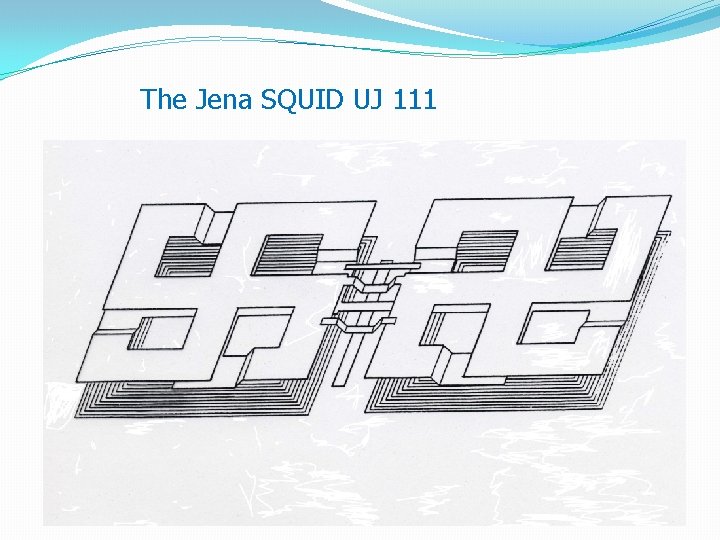
The Jena SQUID UJ 111

UJ 111 (with lead shield) FSU Jena 1984 Nb-Pb thin film technology

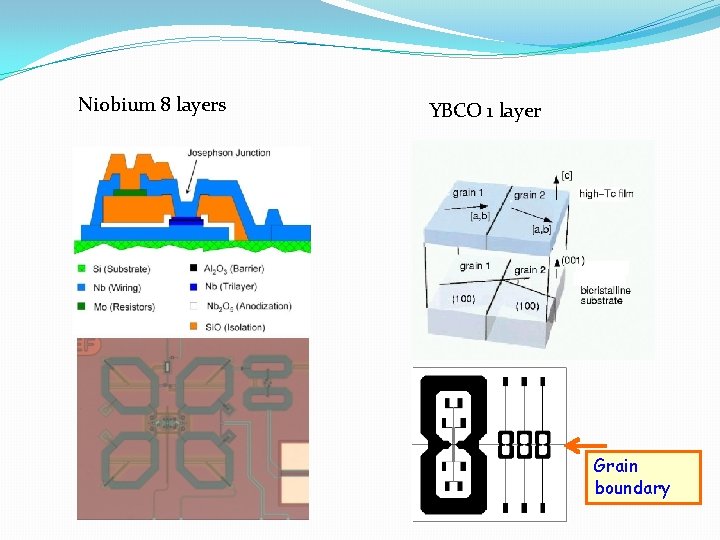
Niobium 8 layers YBCO 1 layer Grain boundary

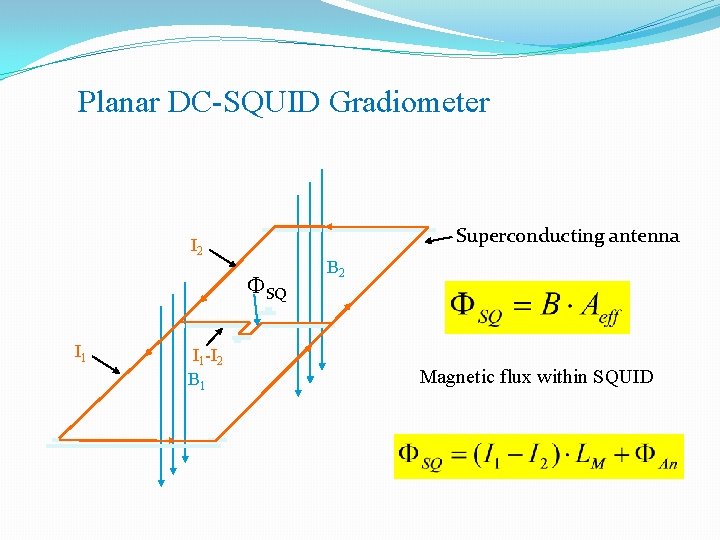
Planar DC-SQUID Gradiometer Superconducting antenna I 2 FSQ I 1 -I 2 B 1 B 2 Magnetic flux within SQUID

F. Schmidl, A. Zakasarenko, E. Il`ichev, P. Seidel

HTS DC-SQUID Gradiometer


Flux transformer




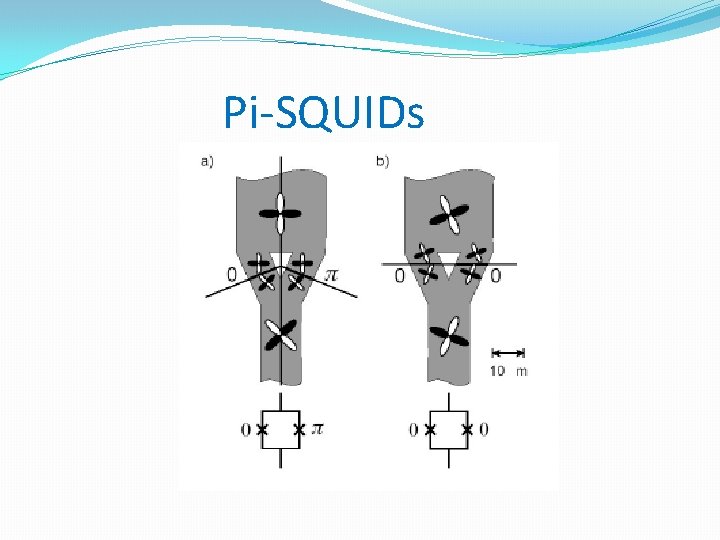
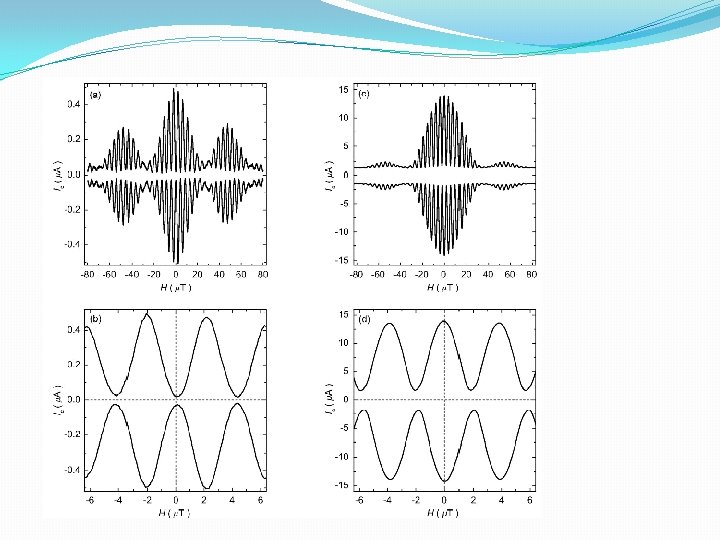
Pi-SQUIDs
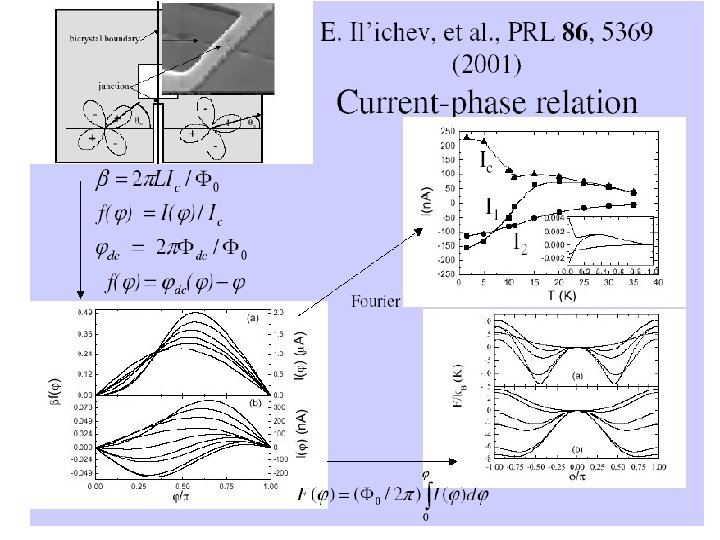
![Chesca [Chesca]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-68.jpg)
[Chesca]


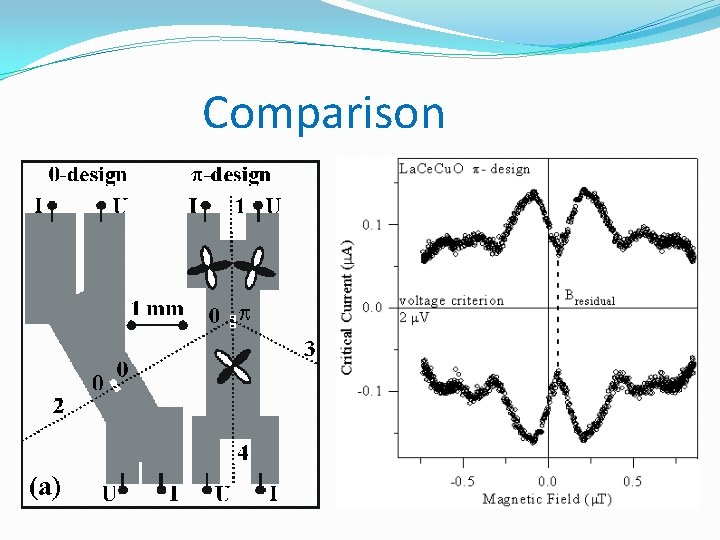
Comparison

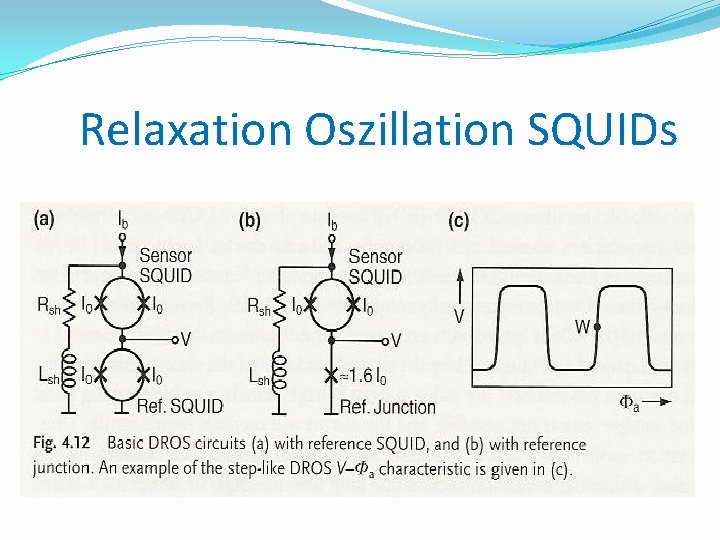
Relaxation Oszillation SQUIDs

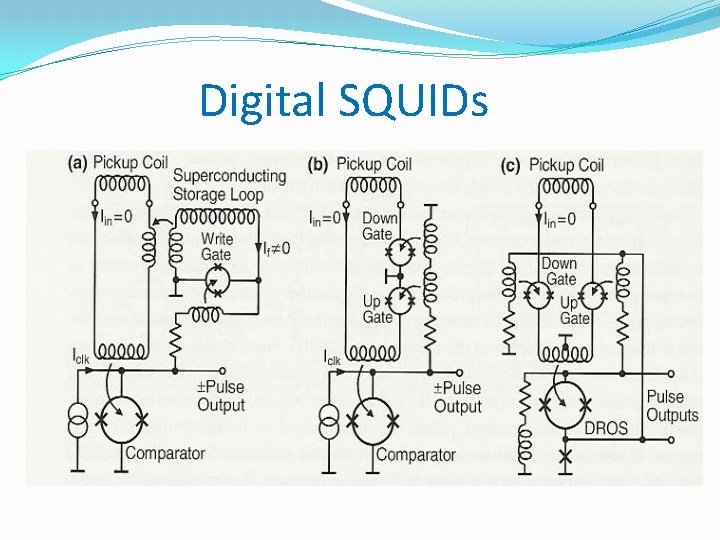
Digital SQUIDs

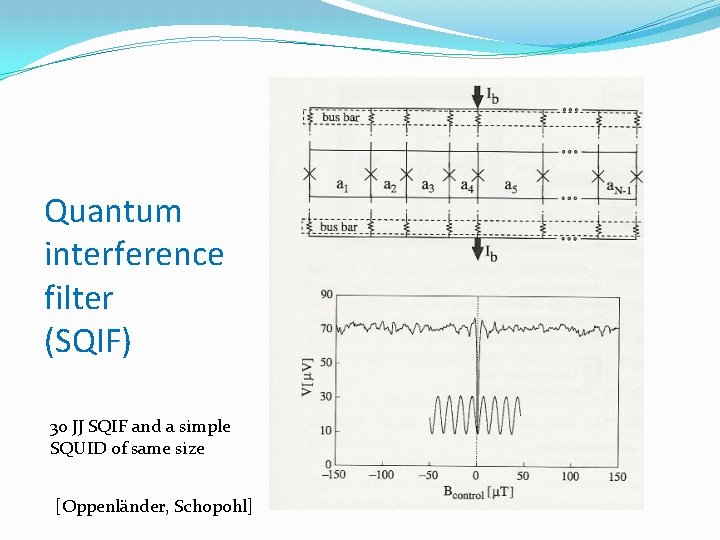
Quantum interference filter (SQIF) 30 JJ SQIF and a simple SQUID of same size [Oppenländer, Schopohl]
![Serial SQIF Schultze Serial SQIF [Schultze]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-74.jpg)
Serial SQIF [Schultze]
![2 p T Hz IPHT Jena 2 p. T / √ Hz [IPHT Jena]}](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-75.jpg)
2 p. T / √ Hz [IPHT Jena]}
![2 D SQIF array R Fagaly 2 D- SQIF array [R. Fagaly]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-76.jpg)
2 D- SQIF array [R. Fagaly]
![BiSQUID R Fagaly Bi-SQUID [R. Fagaly]](https://slidetodoc.com/presentation_image_h2/81def57c997796372a709fb5fc171f16/image-77.jpg)
Bi-SQUID [R. Fagaly]