Quantum Computing MAS 725 Hartmut Klauck NTU 26

Quantum Computing MAS 725 Hartmut Klauck NTU 26. 3. 2012

Order finding over ZN l l l We are given x, N, x<N Order r(x) of x in ZN: min. r 0: xr =1 mod N „Period“ of the powers x

Order finding over ZN l l l Is there a quantum algorithm to find r(x)? Shor‘s algorithm finds r(x) in time poly(log N) trivial approach: compute xi for i=1, . . . , r(x) • this is inefficient, could be that r(x)=N-1

Application l l Factorization problem: Given a natural number N, find some nontrivial prime factor (or even all of them) Factorization can be reduced to order finding! • Purely classical reduction

Shor‘s algorithm ¢ ¢ ¢ We follow the general outline of Simon‘s algorithm Start with Hadamard transform, query the black box But then we need another transformation, the quantum Fourier transform

Fourier Transform ¢ Fourier transform: l g is a function ZL ! C [or a vector with L entries] l ¢ ¢ ¢ Let w=e 2 i/L. Then the Fourier transform is a linear map with matrix FTL(i, j)=wij; 0· i, j· L-1 The trivial algorithm to compute the Fourier transform takes time O(L 2) Fast Fourier Transform [FFT] takes times O(L log L)

Quantum Fourier Transform ¢ ¢ ¢ Set L=2 n. Consider the state | i= j=0, . . . , L-1 j |ji. The Fourier transform of | i is | i = j=0, . . . , L-1 j |ji, with This is just the Fourier transform on the superposition Also called QFT Can we implement the QFT efficiently? Efficient means here: polynomial in n=log L

Quantum Fourier Transform ¢ ¢ ¢ Let L=2 n. Consider | i= j=0, . . . , L-1 j |ji Write j=j 1 jn; j = j 12 n-1 + +jn 20 Set 0. jt jt+1. . . jn = jt/2+ +jn/2 n-t+1 QFT has the following product representation: |j 1. . . jni maps to 2 i 0. jt. . . jn |1 i) 1/2 n/2 ¢ (|0 i+ e t=n, . . . , 1 2 ij/2 t |1 i) =1/2 n/2 ¢ (|0 i+ e t=1, . . . , n

Quantum Fourier Transform ¢ ¢ ¢ |j 1. . . jni is mapped to 2 i 0. jt. . . jn |1 i) 1/2 n/2 ¢ t=n, . . . , 1 (|0 i+ e Let Rk be the following gate/unitary operator Apply H to j 1. Result: 1/21/2 ¢ (|0 i+ e 2 i 0. j 1 |1 i) |j 2, . . . , jni Now apply the Rt gate controlled by jt for t=2, . . . , n to the first qubit. Result: 1/21/2 ¢ (|0 i+ e 2 i 0. j 1, . . . , jn |1 i) |j 2, . . . , jni First qubit is now correct (corresponds to last desired qubit)

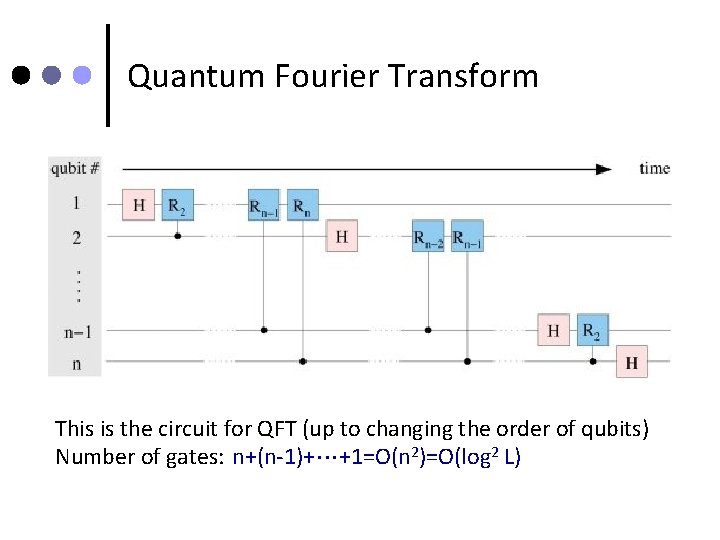
Quantum Fourier Transform This is the circuit for QFT (up to changing the order of qubits) Number of gates: n+(n-1)+ +1=O(n 2)=O(log 2 L)

Quantum Fourier Transform ¢ Caveat: The result of the QFT is a superposition , there is no exponential speedup of computing the Fourier transform in the classical sense (computing the whole vector)

Properties of the QFT ¢ ¢ ¢ Computes in time O(n 2), ie. can als be approximated by standard gates quickly QFT is unitary Set w=e 2 i/L, then FT-1 L(i, j)=w-ij; 0· i, j· L-1 Translation invariance: Let QFT j=0, . . . , L-1 j |ji = j=0, . . . , L-1 j |ji l Tk: |ji |j+k mod Li. QFT Tk j=0, . . . , L-1 j |ji = QFT j=0, . . . , L-1 j |j+k mod Li = j=0, . . . L-1 e 2 ijk/L j |ji

Period finding ¢ Function f: ZL!ZN given as black box Promise: there is a r<N: l f(i)=f(i+r) for all i 2 ZL i j+kr ) f(i) f(j) Find r Try to solve this for arbitrary f Black box: l Uf: |ji |yi |ji |f(j) yi; j 2 ZL; f(j)y 2 ZN l ¢ ¢ Note that Order finding is an instance of Period finding with f(i)=xi

Shor‘s Algorithm ¢ ¢ ¢ ¢ log L+log N work space log L qubits in |0 i ; 02 ZL log N qubits in |1 i; 12 ZN Apply Hadamard on the first register Apply Uf Result: Measure second register Result:

Shor‘s Algorithm ¢ Result: ¢ 0 · j 0 · r-1; L-r · j 0+(A-1)r · L-1 A-1 < L/r < A+1 ¢ ¢

Shor‘s Algorithm ¢ Result: ¢ Now apply QFT Result: ¢ ¢ i. e. the probability of k is independent of j 0 (translation invariance)

Shor‘s Algorithm ¢ Result: ¢ Measurement now: Probability of k is ¢ Assumption : r is a divisor of L, i. e. A=L/r, then

Shor‘s Algorithm ¢ Assumption : r is a divisor of L, i. e. A=L/r, then If A is a divisor of k, then =1/r l If A is no divisor of k, then =0 (because there are r values k that are multiples of A, each contributing probability 1/r) I. e. we receive a multiple of A=L/r, say, c. L/r with 0· c· r-1 With high probability: c and L/r have no common divisor Then gcd(c. L/r, L)=L/r, L is known, hence we learn r. l ¢ ¢ ¢

Shor‘s Algorithm ¢ In general: the probability of k is ¢ ¢ „favorizes“ values of k with kr/L close to an integer Geometric sum ¢ with k=2 kr (mod L)/ L

Shor‘s Algorithm ¢ ¢ with k=2 (kr (mod L))/ L There are exactly r values k 2 ZL with -r/2· kr (mod L) · r/2 For those also - r/L· k· r/L i. e. with 0· j· A-1<L/r the angles j k all lie in the same halfspace ) constructive interference! Call such a k good

Shor‘s Algorithm ¢ ¢ Some bounds: |1 -ei k|· | k| [direct distance „ 1“ to „ei k“ is smaller than the length of the arc] |1 -ei. A k|¸ 2 A| k|/ , if A| k|· Set dist(0, )=|1 -ei |, then dist(0, )/| |¸ dist(0, )/ =2/ A < (L/r)+1, hence A k · A r/L < (1+r/L) l use that kr· r/2 for a good k

Shor‘s Algorithm |1 -ei k|· | k| ; |1 -ei. A k|¸ 2 A| k|/ , if A| k|· A k · A r/L < (1+r/L)

Shor‘s Algorithm ¢ ¢ ¢ ¢ Each of the r good values of k has probability close to 1/r, hence with constant probability we get a k with -r/2· kr (mod L) · r/2 [Success] |kr-c. L|· r/2 for some c Then: |k/L-c/r|· 1/(2 L), i. e. k/L is approximation of c/r We know k and L. Consider k/L as rational number (reduced). c is uniformly random from 0, . . . , r-1 c and r have no common divisor with probability at least 1/log r Then: computing c/r (as a rational number in reduced form) gives us also r Choose L large enough to get a good approximation

Shor‘s Algorithm ¢ ¢ ¢ ¢ With constant probability we get k with |k/L-c/r|· 1/(2 L) With probability 1/log r > 1/log L we have gcd(c, r)=1 Let r<N, L=N 2 c/r is a rational number with denominator <N Any two such numbers are not closer than 1/N 2=1/L > 1/(2 L) The interval contains only one rational number c/r with denominator < N Find the rational number with denominator < N that is close to k/L Use the continued fractions algorithm to do that

Continued fractions ¢ ¢ The continued fractions algorithm computed for a real its representation as continued fraction If |c/r- |· 1/(2 r 2), then one of the steps computes the pair c, r , after at most. O(t 3) Operations for t-bit numbers

Total running time/success probability ¢ ¢ k is good with constant probability With probability 1/log N also c is good (i. e. no common divisor with r) Need to repeat only O(log N) times l For order finding in ZN choose L=N 2, i. e. 2 log N +log N qubits are used l Fourier transform in O(log 2 L) l Continued fractions finds r from k/L in time O(log 3 L) l Can check r for correctness using the black box Total time is O(log 4 N), can be reduced to O(log 3 N)

Continued fractions ¢ ¢ Given: real Approximate by Take integer part as a 0, invert remaining number, iterate Theorem: |p/q- |· 1/(2 q 2), then p/q appears after at most O(log (p+q)) steps