Notes Quantum Mechanics AP Physics B Quantum Quantum

Notes : _____ Quantum Mechanics AP Physics B

Quantum? Quantum mechanics is the study of processes which occur at the atomic scale. The word "quantum" is derived From Latin to mean BUNDLE. Therefore, we are studying the motion of objects that come in small bundles called quanta. These tiny bundles that we are referring to are electrons traveling around the nucleus.

“Newton, forgive me. . ”, Albert At the atomic scale Newtonian Mechanics Einstein cannot seem to describe the motion of particles. An electron trajectory between two points for example IS NOT a perfect parabolic trajectory as Newton's Laws predicts. Where Newton's Laws end Quantum Mechanics takes over. . . IN A BIG WAY! One of the most popular concepts concerning Quantum Mechanics is called , “The Photoelectric Effect”. In 1905, Albert Einstein published this theory for which he won the Nobel Prize in 1921.

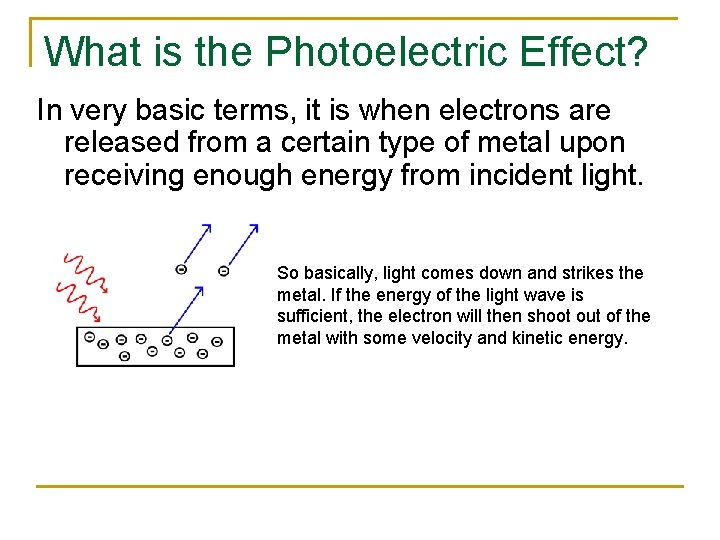
What is the Photoelectric Effect? In very basic terms, it is when electrons are released from a certain type of metal upon receiving enough energy from incident light. So basically, light comes down and strikes the metal. If the energy of the light wave is sufficient, the electron will then shoot out of the metal with some velocity and kinetic energy.

The Electron-Volt = ENERGY Before we begin to discuss the photoelectric effect, we must introduce a new type of unit. Recall: This is a very useful unit as it shortens our calculations and allows us to stray away from using exponents.

The Photoelectric Effect "When light strikes a material, electrons are emitted. The radiant energy supplies the work necessary to free the electrons from the surface. "

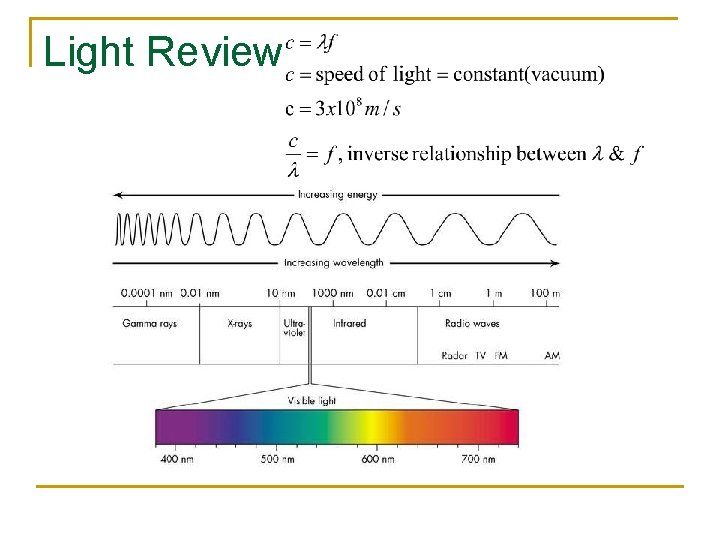
Photoelectric Fact #1 The LIGHT ENERGY (E) is in the form of quanta called PHOTONS. Since light is an electromagnetic wave it has an oscillating electric field. The more intense the light the more the field oscillates. In other words, its frequency is greater.

Light Review

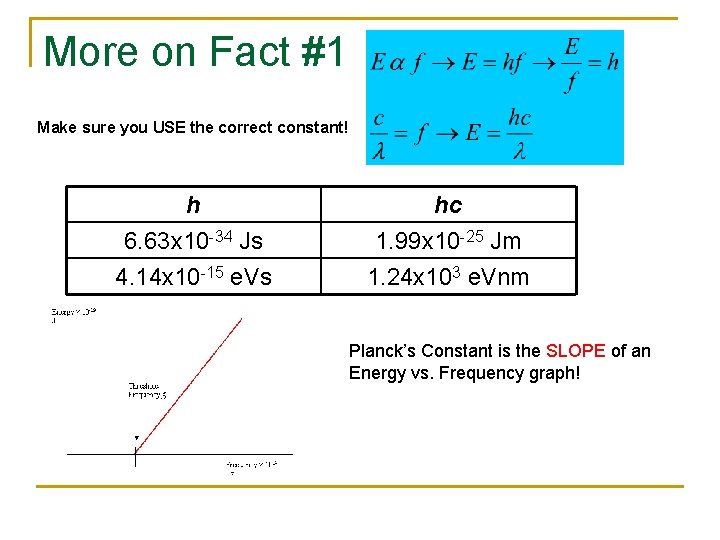
More on Fact #1 Make sure you USE the correct constant! h 6. 63 x 10 -34 Js 4. 14 x 10 -15 e. Vs hc 1. 99 x 10 -25 Jm 1. 24 x 103 e. Vnm Planck’s Constant is the SLOPE of an Energy vs. Frequency graph!

Photoelectric Fact #2 The frequency of radiation must be above a certain value before the energy is enough. This minimum frequency required by the source of electromagnetic radiation to just liberate electrons from the metal is known as threshold frequency, f 0. The threshold frequency is the X-intercept of the Energy vs. Frequency graph!

Photoelectric Fact #3 Work function, f, is defined as the least energy that must be supplied to remove a free electron from the surface of the metal, against the attractive forces of surrounding positive ions. Shown here is a PHOTOCELL. When incident light of appropriate frequency strikes the metal (cathode), the light supplies energy to the electron. The energy need to remove the electron from the surface is the WORK! Not ALL of the energy goes into work! As you can see the electron then MOVES across the GAP to the anode with a certain speed and kinetic energy.

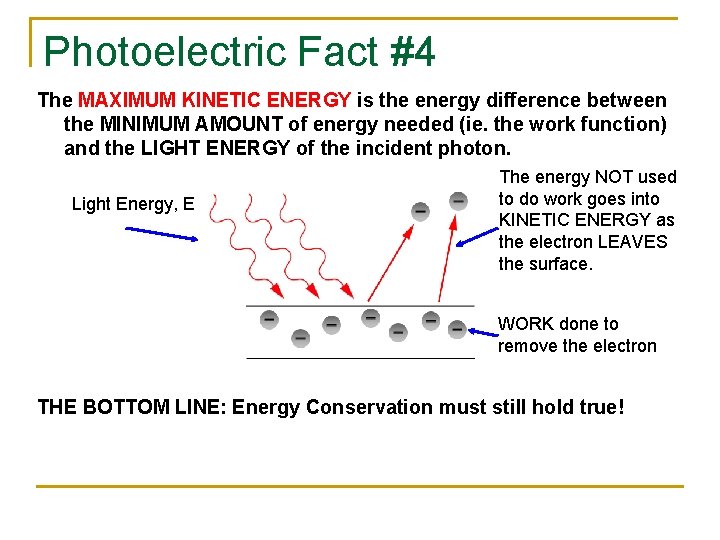
Photoelectric Fact #4 The MAXIMUM KINETIC ENERGY is the energy difference between the MINIMUM AMOUNT of energy needed (ie. the work function) and the LIGHT ENERGY of the incident photon. Light Energy, E The energy NOT used to do work goes into KINETIC ENERGY as the electron LEAVES the surface. WORK done to remove the electron THE BOTTOM LINE: Energy Conservation must still hold true!

Putting it all together KINETIC ENERGY can be plotted on the y axis and FREQUENCY on the xaxis. The WORK FUNCTION is the y – intercept as the THRESHOLD FREQUNECY is the x intercept. PLANCK‘S CONSTANT is the slope of the graph.

n n n KE max = hf – hfo KE max = hf ( energy of the original photon ) – hfo (Work function- property of the metal) Work function is the minimum energy needed to free an electron.

PROBLEM n n Light with frequency of 2 X 10 15 hertz is incident on a piece of copper. A. what is the energy of light in joules and in electron volt? If the work function for copper is 4. 5 e. V , what is the maximum kinetic energy , in electron volts of the emitted electrons ? Note : 1 e. V = 1. 6 X 10 -19 J

A. the energy in joules is given by E= hf E = hf = (6. 63 X 10 -34 ) ( 2 X 1015) = E= 1. 326 X 10 -16 J n Since 1 e. V = 1. 6 X 10 -19 J E= 8. 28 e. V B. To find the maximum kinetic energy , we simply subtract the work function from the photon energy. KEmax = 8. 28 V – 4. 5 V = 3. 79 e. V

Can we use this idea in a circuit? We can then use this photoelectric effect idea to create a circuit using incident light. Of course, we now realize that the frequency of light must be of a minimum frequency for this work. Notice the + and – on the photocell itself. We recognize this as being a POTENTIAL DIFFERENCE or Voltage. This difference in voltage is represented as a GAP that the electron has to jump so that the circuit works What is the GAP or POTENTIAL DIFFERENCE is too large?

Photoelectric Fact #5 - Stopping If the voltage is TOO LARGE the electrons WILL NOT have Potential enough energy to jump the gap. We call this VOLTAGE point the STOPPING POTENTIAL. If the voltage exceeds this value, no photons will be emitted no matter how intense. Therefore it appears that the voltage has all the control over whether the photon will be emitted and thus has kinetic energy.

Wave-Particle Duality The results of the photoelectric effect allowed us to look at light completely different. First we have Thomas Young’s Diffraction experiment proving that light behaved as a WAVE due to constructive and destructive interference. Then we have Max Planck who allowed Einstein to build his photoelectric effect idea around the concept that light is composed of PARTICLES called quanta.

This led to new questions…. If light is a WAVE and is ALSO a particle, does that mean ALL MATTER behave as waves? That was the question that Louis de Broglie pondered. He used Einstein's famous equation to answer this question.

YOU are a matter WAVE! Basically all matter could be said to have a momentum as it moves. The momentum however is inversely proportional to the wavelength. So since your momentum would be large normally, your wavelength would be too small to measure for any practical purposes. An electron, however, due to it’s mass, would have a very small momentum relative to a person and thus a large enough wavelength to measure thus producing measurable results. This led us to start using the Electron Microscopes rather than traditional Light microscopes.

Problem Find the de Broglie wavelength for each of the following : a. A 10 g stone moving with a velocity of 20 m/s b. An electron (9. 1 X 10 -31) kg moving with a velocity of 1 X 107 m/s

since m =10 g = 0. 01 kg and λ = h/mv λ = 6. 63 X 10 -34 --------- = 3. 315 X 10 -33 m (0. 01)( 20) b. In this part , we have λ = h / mv = 6. 63 X 10 -34 --------- = 7. 3 X 10 -11 m (9. 1 X 10 -31)(1 X 10 -7) a.

The electron microscope After the specimen is prepped. It is blasted by a bean of electrons. As the incident electrons strike the surface, electrons are released from the surface of the specimen. The de. Broglie wavelength of these released electrons vary in wavelength which can then be converted to a signal by which a 3 D picture can then be created based on the signals captured by the detector.

CW: Problems 1. What is the Broglie wavelength for a proton ( m = 1. 67 X 10 -27 kg ) with a velocity of 6 X 10 7 m/s 2. What is the momentum associated with yellow light that has wavelength of 5, 500 Å 1Å = Å X 10 -10 m

n 1. 6. 6 X 10 -15 m n 2. 1. 2 X 10 -27 kg m/s

Atomic & Nuclear Physics AP Physics B

Objectives: After completing this module, you should be able to: • Define and apply the concepts of mass number, atomic number, and isotopes. • Calculate the mass defect and the binding energy per nucleon for a particular isotope. • Define and apply concepts of radioactive decay and nuclear reactions. • State the various conservation laws, and discuss their application for nuclear reactions.

Life and Atoms Every time you breathe you are taking in atoms. Oxygen atoms to be exact. These atoms react with the blood and are carried to every cell in your body for various reactions you need to survive. Likewise, every time you breathe out carbon dioxide atoms are released. The cycle here is interesting. TAKING SOMETHING IN. ALLOWING SOMETHING OUT!

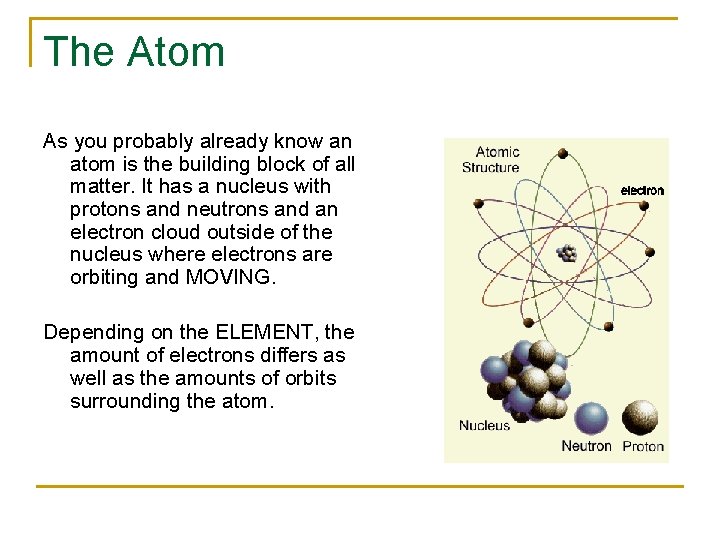
The Atom As you probably already know an atom is the building block of all matter. It has a nucleus with protons and neutrons and an electron cloud outside of the nucleus where electrons are orbiting and MOVING. Depending on the ELEMENT, the amount of electrons differs as well as the amounts of orbits surrounding the atom.

Composition of Matter All of matter is composed of at least three fundamental particles (approximations): Particle Fig. Sym Mass Charge Size 9. 11 x 10 -31 kg -1. 6 x 10 -19 C Electron e- Proton p 1. 673 x 10 -27 kg +1. 6 x 10 -19 C 3 fm Neutron n 1. 675 x 10 -31 kg 0 3 fm The mass of the proton and neutron are close, but they are about 1840 times the mass of an electron.

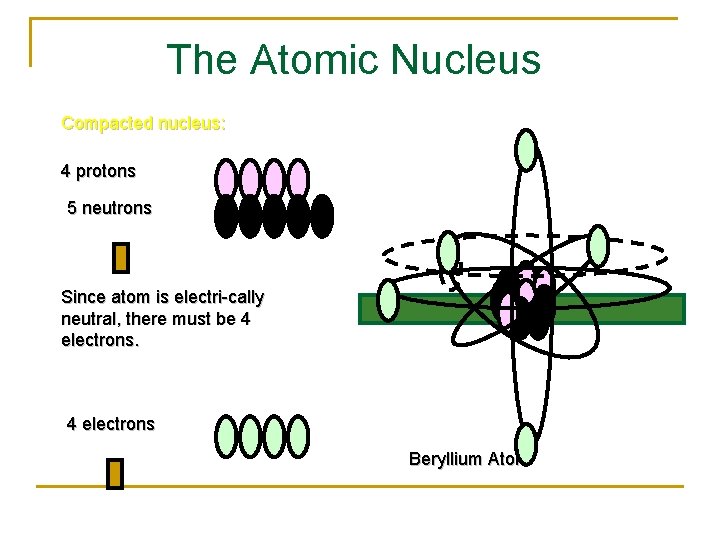
The Atomic Nucleus Compacted nucleus: 4 protons 5 neutrons Since atom is electri-cally neutral, there must be 4 electrons Beryllium Atom

Modern Atomic Theory The Bohr atom, which is sometimes shown with electrons as planetary particles, is no longer a valid representation of an atom, but it is used here to simplify our discussion of energy levels. The uncertain position of an electron is now described as a probability distribution—loosely referred to as an electron cloud.

Definitions A nucleon is a general term to denote a nuclear particle - that is, either a proton or a neutron. The atomic number Z of an element is equal to the number of protons in the nucleus of that element. The mass number A of an element is equal to the total number of nucleons (protons + neutrons). The mass number A of any element is equal to the sum of the atomic number Z and the number of neutrons N : A=N+Z

Symbol Notation A convenient way of describing an element is by giving its mass number and its atomic number, along with the chemical symbol for that element. For example, consider beryllium (Be):

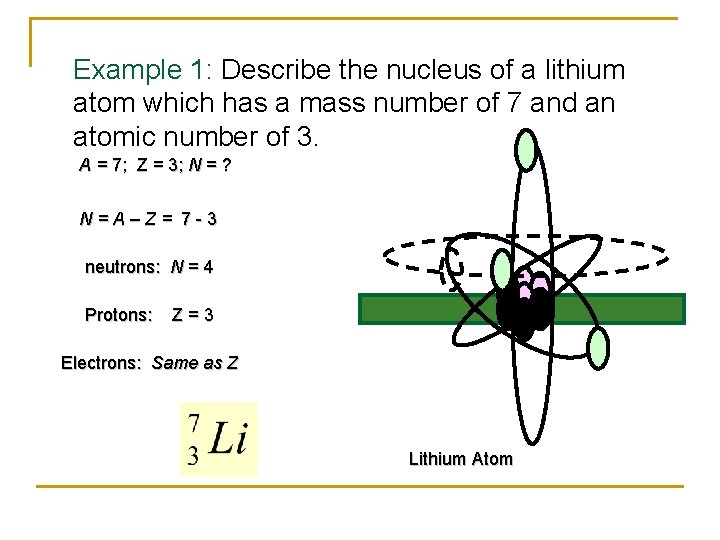
Example 1: Describe the nucleus of a lithium atom which has a mass number of 7 and an atomic number of 3. A = 7; Z = 3; N = ? N = A – Z = 7 - 3 neutrons: N = 4 Protons: Z = 3 Electrons: Same as Z Lithium Atom

When the atom gets excited or NOT To help visualize the atom think of it like a ladder. The bottom of the ladder is called GROUND STATE where all electrons would like to exist. If energy is ABSORBED it moves to a new rung on the ladder or ENERGY LEVEL called an EXCITED STATE. This state is AWAY from the nucleus. As energy is RELEASED the electron can relax by moving to a new energy level or rung down the ladder.

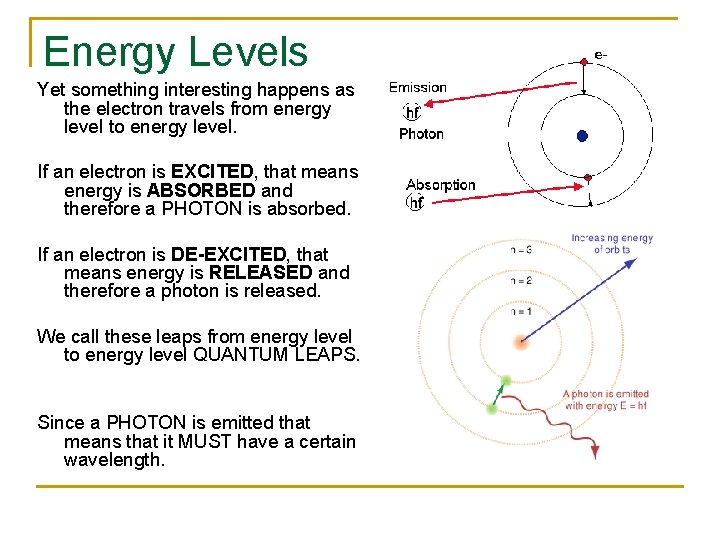
Energy Levels Yet something interesting happens as the electron travels from energy level to energy level. If an electron is EXCITED, that means energy is ABSORBED and therefore a PHOTON is absorbed. If an electron is DE-EXCITED, that means energy is RELEASED and therefore a photon is released. We call these leaps from energy level to energy level QUANTUM LEAPS. Since a PHOTON is emitted that means that it MUST have a certain wavelength.

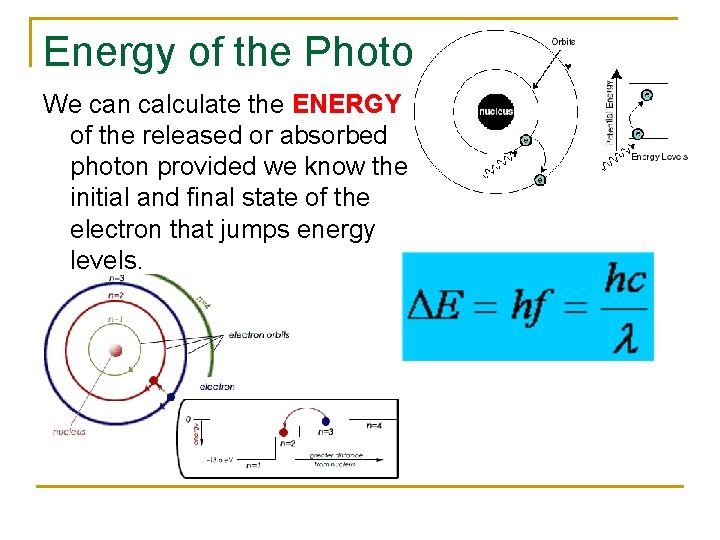
Energy of the Photon We can calculate the ENERGY of the released or absorbed photon provided we know the initial and final state of the electron that jumps energy levels.

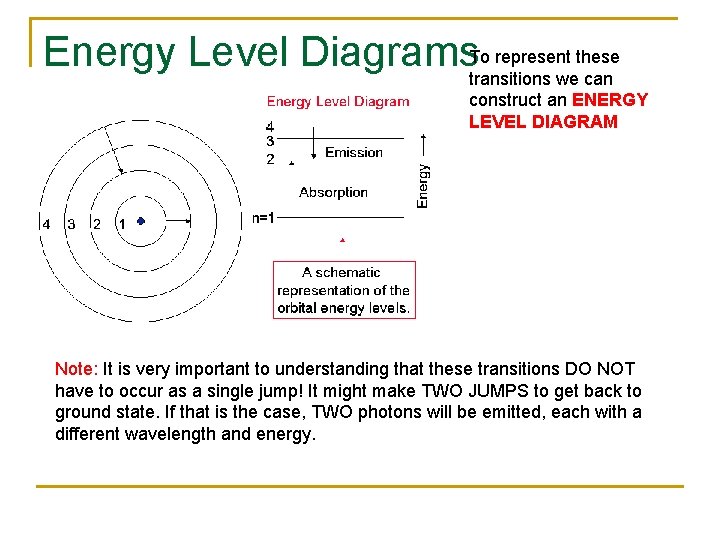
Energy Level Diagrams. To represent these transitions we can construct an ENERGY LEVEL DIAGRAM Note: It is very important to understanding that these transitions DO NOT have to occur as a single jump! It might make TWO JUMPS to get back to ground state. If that is the case, TWO photons will be emitted, each with a different wavelength and energy.

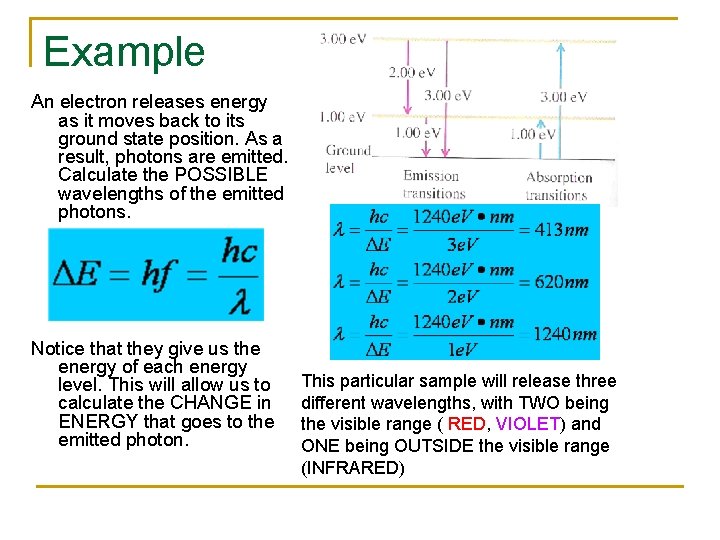
Example An electron releases energy as it moves back to its ground state position. As a result, photons are emitted. Calculate the POSSIBLE wavelengths of the emitted photons. Notice that they give us the energy of each energy level. This will allow us to calculate the CHANGE in ENERGY that goes to the emitted photon. This particular sample will release three different wavelengths, with TWO being the visible range ( RED, VIOLET) and ONE being OUTSIDE the visible range (INFRARED)

Energy levels Application: Spectroscopy is an optical technique by which we can IDENTIFY a material based on its emission spectrum. It is heavily used in Astronomy and Remote Sensing. There are too many subcategories to mention here but the one you are probably the most familiar with are flame tests. When an electron gets excited inside a SPECIFIC ELEMENT, the electron releases a photon. This photon’s wavelength corresponds to the energy level jump and can be used to indentify the element.

Different Elements = Different Emission Lines

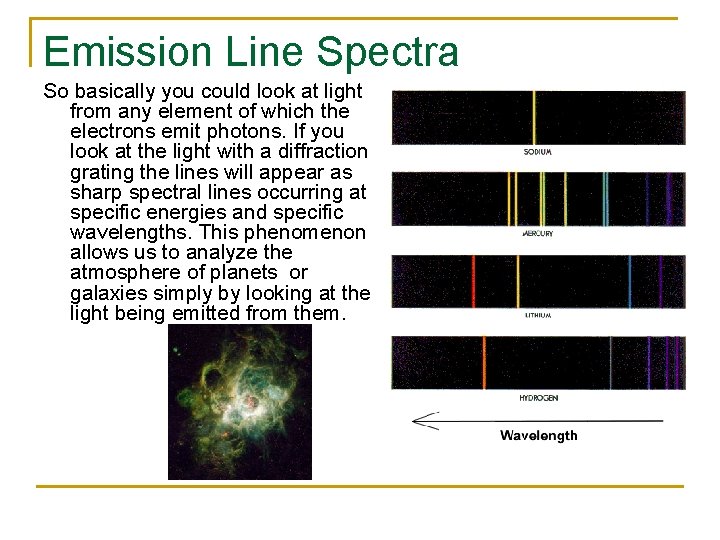
Emission Line Spectra So basically you could look at light from any element of which the electrons emit photons. If you look at the light with a diffraction grating the lines will appear as sharp spectral lines occurring at specific energies and specific wavelengths. This phenomenon allows us to analyze the atmosphere of planets or galaxies simply by looking at the light being emitted from them.

Nuclear Physics - Radioactivity Before we begin to discuss the specifics of radioactive decay we need to be certain you understand the proper NOTATION that is used. To the left is your typical radioactive isotope. Top number = mass number = #protons + neutrons. It is represented by the letter "A“ Bottom number = atomic number = # of protons in the nucleus. It is represented by the letter "Z"

Nuclear Physics – Notation & Isotopes An isotope is when you have the SAME ELEMENT, yet it has a different MASS. This is a result of have extra neutrons. Since Carbon is always going to be element #6, we can write Carbon in terms of its mass instead. Carbon - 12 Carbon - 14

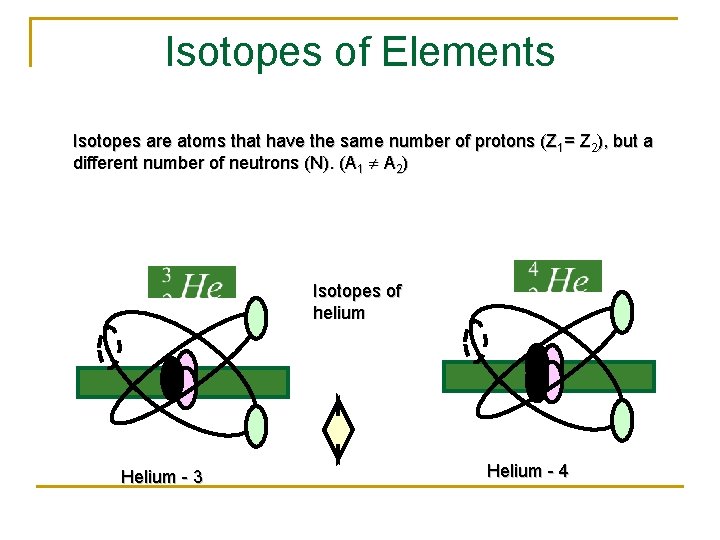
Isotopes of Elements Isotopes are atoms that have the same number of protons (Z 1= Z 2), but a different number of neutrons (N). (A 1 A 2) Isotopes of helium Helium - 3 Helium - 4

Atomic Mass Unit, u One atomic mass unit (1 u) is equal to one-twelfth of the mass of the most abundant form of the carbon atom--carbon-12. Atomic mass unit: 1 u = 1. 6606 x 10 -27 kg Common atomic masses: Proton: 1. 007276 u Neutron: 1. 008665 u Electron: 0. 00055 u Hydrogen: 1. 007825 u

Einstein – Energy/Mass Equivalence. In 1905, Albert Einstein publishes a 2 theory called the Energy-Mass nd major Equivalence in a paper called, “Does the inertia of a body depend on its energy content? ”

Einstein – Energy/Mass Looking closely at Einstein’s equation we see that he Equivalence postulated that mass held an enormous amount of energy within itself. We call this energy BINDING ENERGY or Rest mass energy as it is the energy that holds the atom together when it is at rest. The large amount of energy comes from the fact that the speed of light is squared.

Energy Unit Check

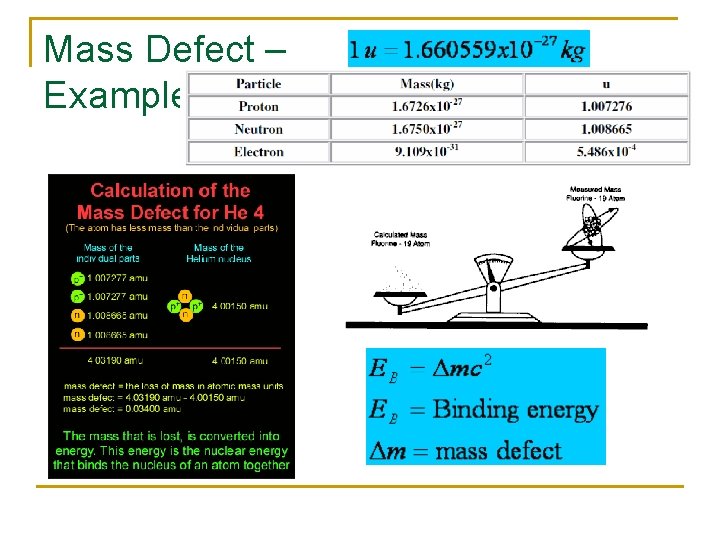
Mass Defect The nucleus of the atom is held together by a STRONG NUCLEAR FORCE. The more stable the nucleus, the more energy needed to break it apart. Energy need to break the nucleus into protons and neutrons is called the Binding Energy Einstein discovered that the mass of the separated particles is greater than the mass of the intact stable nucleus to begin with. This difference in mass (Dm) is called the mass defect.

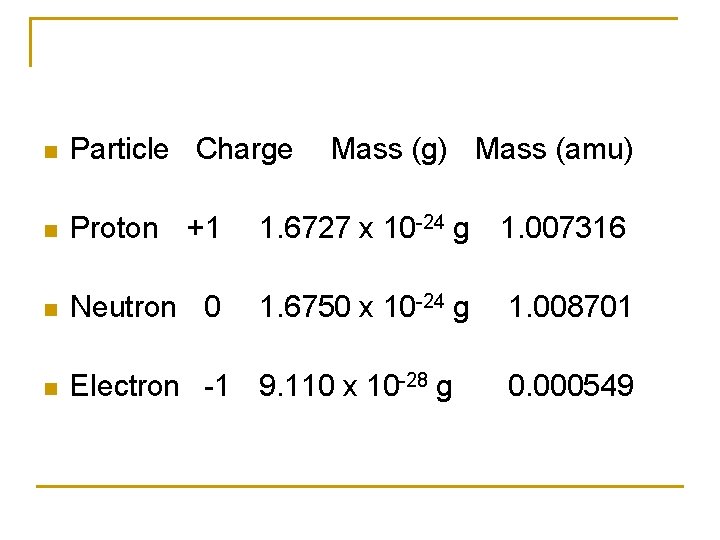
n Particle Charge Mass (g) Mass (amu) n Proton +1 1. 6727 x 10 -24 g 1. 007316 n Neutron 0 1. 6750 x 10 -24 g 1. 008701 n Electron -1 9. 110 x 10 -28 g 0. 000549

Mass Defect - Explained The extra mass turns into energy holding the atom together.

Binding Energy is proportional to the mass defect. The energy equivalent of 1 atomic mass unit υ Is equal to 931. 5 million electron volts ( Me. V) Nuclear Mass =Isotope’s Ave Mass – Total electron masses Mass Defect = Mass of the nucleons- Mass of the Nucleus Mass of Nucleons = Zmp + Nmn OR MD = ( Zm. H + Nmn) – M M = atomic mass Binding Energy = Mass Defect , amu X 931. 5 Me. V/ amu Avg BE = BE / mass number = BE / A , Me. V / nucleon

Example 2: The average atomic mass of Boron-11 is 11. 009305 u. What is the mass of the nucleus of one boron atom in kg? Electron: 0. 00055 u The mass of the nucleus is the atomic mass less the mass of Z = 5 electrons:

Example 2: The average atomic mass of Boron-11 is 11. 009305 u. What is the mass of the nucleus of one boron atom in kg? Electron: 0. 00055 u The mass of the nucleus is the atomic mass less the mass of Z = 5 electrons: Mass = 11. 009305 u – 5(0. 00055 u) 1 boron nucleus = 11. 00656 u m = 1. 83 x 10 -26 kg

Mass and Energy Recall Einstein’s equivalency formula for m and E: The energy of a mass of 1 u can be found: E = (1 u)c 2 = (1. 66 x 10 -27 kg)(3 x 108 m/s)2 E = 1. 49 x 10 -10 J When converting amu to energy: Or E = 931. 5 Me. V

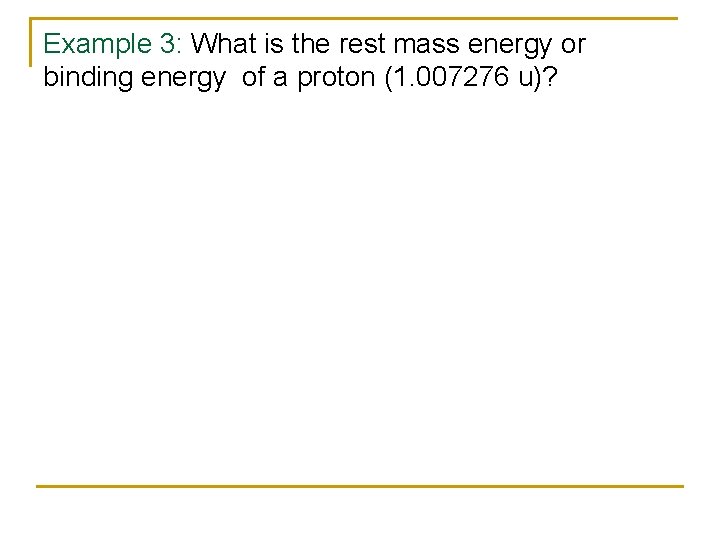
Example 3: What is the rest mass energy or binding energy of a proton (1. 007276 u)?

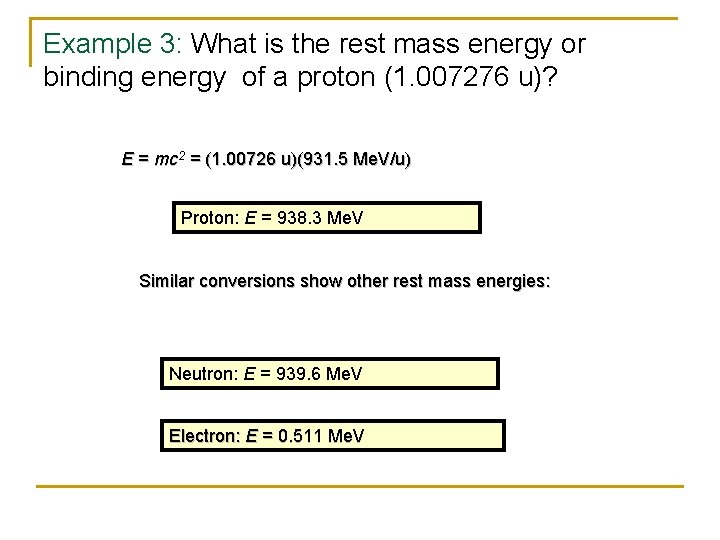
Example 3: What is the rest mass energy or binding energy of a proton (1. 007276 u)? E = mc 2 = (1. 00726 u)(931. 5 Me. V/u) Proton: E = 938. 3 Me. V Similar conversions show other rest mass energies: Neutron: E = 939. 6 Me. V Electron: E = 0. 511 Me. V

Atomic Mass Unit, u One atomic mass unit (1 u) is equal to one-twelfth of the mass of the most abundant form of the carbon atom--carbon-12. Atomic mass unit: 1 u = 1. 6606 x 10 -27 kg Common atomic masses: Proton: 1. 007276 u Neutron: 1. 008665 u Electron: 0. 00055 u Hydrogen: 1. 007825 u

Formula for Mass Defect The following formula is useful for mass defect: Mass defect m. D m. H = 1. 007825 u; mn = 1. 008665 u Z is atomic number; N is neutron number; M is mass of atom (including electrons). By using the mass of the hydrogen atom, you avoid the necessity of subtracting electron masses.

Binding Energy is proportional to the mass defect. The energy equivalent of 1 atomic mass unit υ Is equal to 931. 5 million electron volts ( Me. V) Nuclear Mass =Isotope’s Ave Mass – Total electron masses Mass Defect = Mass of the nucleons- Mass of the Nucleus Mass of Nucleons = Zmp + Nmn OR MD = ( Zm. H + Nmn) – M M = atomic mass Binding Energy = Mass Defect , amu X 931. 5 Me. V/ amu Avg BE = BE / mass number = BE / A , Me. V / nucleon

The Mass Defect The mass defect is the difference between the rest mass of a nucleus and the sum of the rest masses of its constituent nucleons. The whole is less than the sum of the parts! Consider the carbon-12 atom (12. 00000 u): Nuclear mass = Mass of atom – Electron masses = 12. 00000 u – 6(0. 00055 u) = 11. 996706 u The nucleus of the carbon-12 atom has this mass. (Continued. . . )

Mass Defect (Continued) Mass of carbon-12 nucleus: 11. 996706 Proton: 1. 007276 u Neutron: 1. 008665 u The nucleus contains 6 protons and 6 neutrons: 6 p = 6(1. 007276 u) = 6. 043656 u 6 n = 6(1. 008665 u) = 6. 051990 u Total mass of parts: = 12. 095646 u Mass defect m. D = 12. 095646 u – 11. 996706 u m. D = 0. 098940 u

Example 4: Find the mass defect for the nucleus of helium-4. (Mnucleus = 4. 002603 u)

Example 4: Find the mass defect for the nucleus of helium-4. (M = 4. 002603 u) Mass defect m. D Zm. H = (2)(1. 007825 u) = 2. 015650 u Nmn = (2)(1. 008665 u) = 2. 017330 u M = 4. 002603 u (From nuclide tables) m. D = (2. 015650 u + 2. 017330 u) - 4. 002603 u m. D = 0. 030377 u

Binding Energy per Nucleon An important way of comparing the nuclei of atoms is finding their binding energy per nucleon: Binding energy per nucleon For our C-12 example A = 12 and:

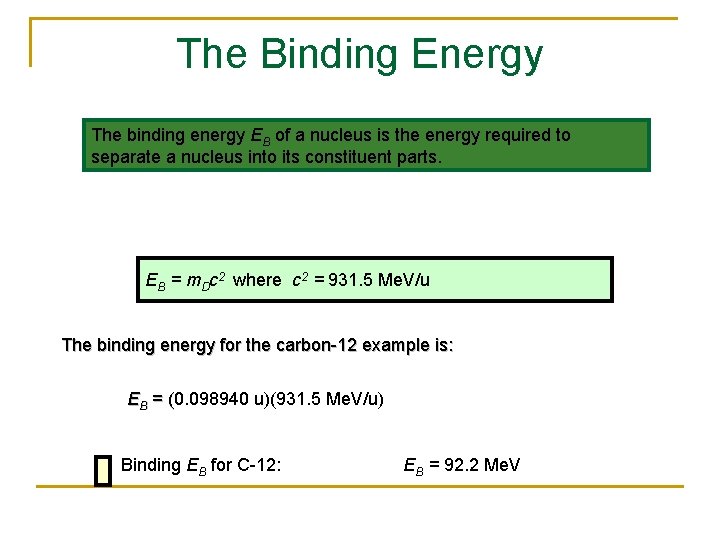
The Binding Energy The binding energy EB of a nucleus is the energy required to separate a nucleus into its constituent parts. EB = m. Dc 2 where c 2 = 931. 5 Me. V/u The binding energy for the carbon-12 example is: EB = (0. 098940 u)(931. 5 Me. V/u) = ( Binding EB for C-12: EB = 92. 2 Me. V

Formula for Mass Defect The following formula is useful for mass defect: Mass defect m. D m. H = 1. 007825 u; mn = 1. 008665 u Z is atomic number; N is neutron number; M is mass of atom (including electrons). By using the mass of the hydrogen atom, you avoid the necessity of subtracting electron masses.

Example 4: Find the mass defect for the nucleus of helium-4. (Mnucleus = 4. 002603 u) Mass defect m. D Zm. H = (2)(1. 007825 u) = 2. 015650 u Nmn = (2)(1. 008665 u) = 2. 017330 u M = 4. 002603 u (From nuclide tables) m. D = (2. 015650 u + 2. 017330 u) - 4. 002603 u m. D = 0. 030377 u

Example 4 (Cont. ) Find the binding energy per nucleon for helium-4. (m. D = 0. 030377 u) EB = m. Dc 2 where c 2 = 931. 5 Me. V/u EB = (0. 030377 u)(931. 5 Me. V/u) = 28. 3 Me. V A total of 28. 3 Me. V is required To tear apart the nucleons from the He-4 atom. Since there are four nucleons, we find that

Mass Defect – Example

Given an isotope 56 which has an actual n 26 Fe mass of 55. 934939 u. a. Determine the mass defect of the nucleus in atomic mass units b. Determine the average binding energy per nucleon in units of million electron volts. n

P = 26(1. 0078 u)= 26. 2028 u N = 30(1. 0087 u)=30. 2610 u Mass Defect = 56. 463800 – 55. 934939 =0. 528861 u BE= 0. 528861 u X 931. 5 Me. V /u = 492. 63402 Mev Average BE = 492. 63402/56 = 8. 797 Me. V

Problem The atomic mass of 27 is 26. 9815 u. What is n 13 Al the nuclear binding energy per nucleon ? ( mass of electron =. 0005486 u)

Mass Nucleus 8. 3 Me. V / nucleon

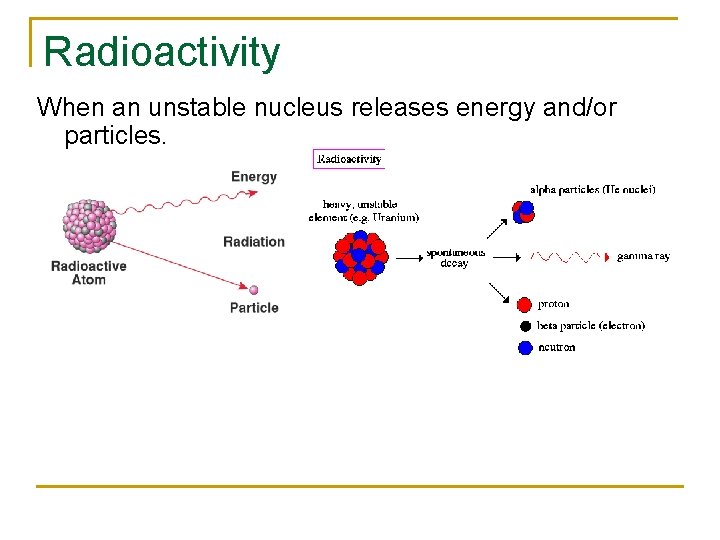
Radioactivity When an unstable nucleus releases energy and/or particles.

En = Z 2 / n 2 ( -13. 6 V ) The minimum amount of energy needed that must be supplied to release the atom’s electrons. En = 1/n 2 E 1 /E final – E initial/ f = ------------- wavelength

Energy Level Diagram for Hydrogen State Energy 6 _______________-0. 38 e. V 5_______________- 0. 54 e. V 4_______________-0. 85 e. V 3_______IR rays_____-1. 5 e. V n 2_____Visible________-3. 4 e. V 1______UV rays_________-13. 4 e. V

What is the wavelength of a photon emitted when an electron makes a transition in a hydrogen atom from level 5 to level 3 ?

E = 1. 536 X 10 -19 J f= 2. 3 X 10 14 Hz Wavelength = 1. 29 X 10 -6 m

Problem : How much energy must a ground –state electron in a Hydrogen atom absorb to be excited to the n=4 energy level ? What is the wavelength of the photon absorbed by hydrogen atom ?

Change in Energy levels = 12. 75 e. V; 2. 04 X 10 -18 J f = 3. 08 X 1015 Hz Wavelength= 9. 78 X 10 -8 m

Radioactive Decay There are 4 basic types of radioactive decay n Alpha – Ejected Helium n Beta – Ejected Electron n Positron – Ejected Anti-Beta particle n Gamma – Ejected Energy You may encounter protons and neutrons being emitted as well

Alpha Decay

Alpha Decay Applications Americium-241, an alpha-emitter, is used in smoke detectors. The alpha particles ionize air between a small gap. A small current is passed through that ionized air. Smoke particles from fire that enter the air gap reduce the current flow, sounding the alarm.

Beta Decay There aren’t really any applications of beta decay other than Betavoltaics which makes batteries from beta emitters. Beta decay, did however, lead us to discover the neutrino.

Beta Plus Decay - Positron Isotopes which undergo this decay and thereby emit positrons include carbon-11, potassium-40, nitrogen 13, oxygen-15, fluorine-18, and iodine-121.

Beta Plus Decay Application - Positron emission tomography (PET) is a nuclear medicine imaging technique which produces a three-dimensional image or picture of functional processes in the body. The system detects pairs of gamma rays emitted indirectly by a positron-emitting radionuclide (tracer), which is introduced into the body on a biologically active molecule. Images of tracer concentration in 3 dimensional space within the body are then reconstructed by computer analysis.

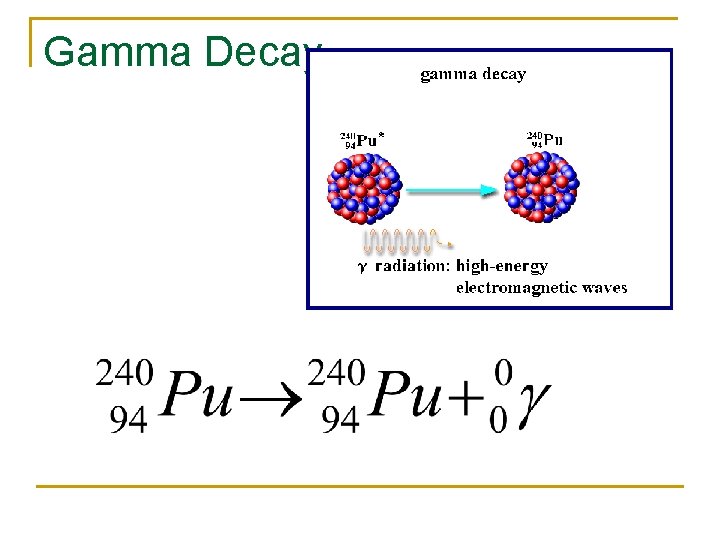
Gamma Decay

Gamma Decay Applications Gamma rays are the most dangerous type of radiation as they are very penetrating. They can be used to kill living organisms and sterilize medical equipment before use. They can be used in CT Scans and radiation therapy. Gamma Rays are used to view stowaways inside of a truck. This technology is used by the Department of Homeland Security at many ports of entry to the US.

Significant Nuclear Reactions - Fusion nuclear fusion is the process by which multiple like-charged atomic nuclei join together to form a heavier nucleus. It is accompanied by the release or absorption of energy.

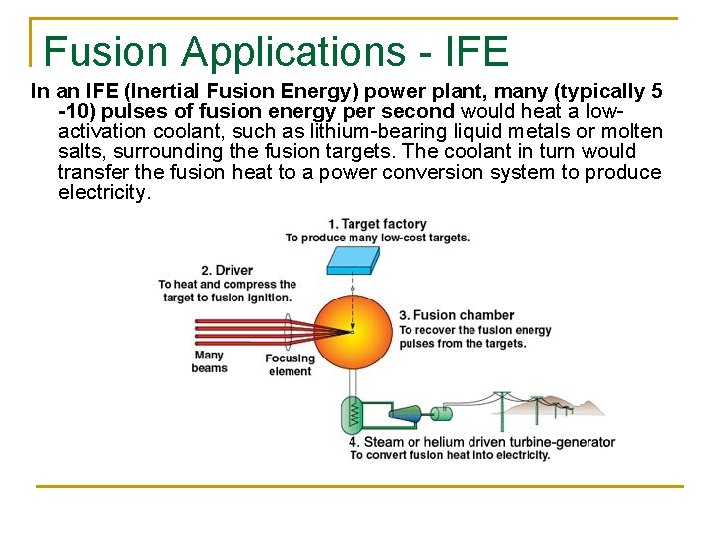
Fusion Applications - IFE In an IFE (Inertial Fusion Energy) power plant, many (typically 5 -10) pulses of fusion energy per second would heat a lowactivation coolant, such as lithium-bearing liquid metals or molten salts, surrounding the fusion targets. The coolant in turn would transfer the fusion heat to a power conversion system to produce electricity.

CW: PROBLEMS COMPLETE THE EQUATIONS: 1. 238 4 92 U 2 He + ? What decay is this ? 2. 234 90 Th 91 Pa + ? What kind of decay is this ?

3. 64 o ? 29 Cu + -1 e What process is the above equation ? o 29 Cu 1 e + ? What decay is this ? 4. 64

1. 234 91 Th Alpha particle decay 2. o -1 e Beta decay 3. 64 28 Ni electron capture 3. Transmutation 4. 64 28 Ni positron emission

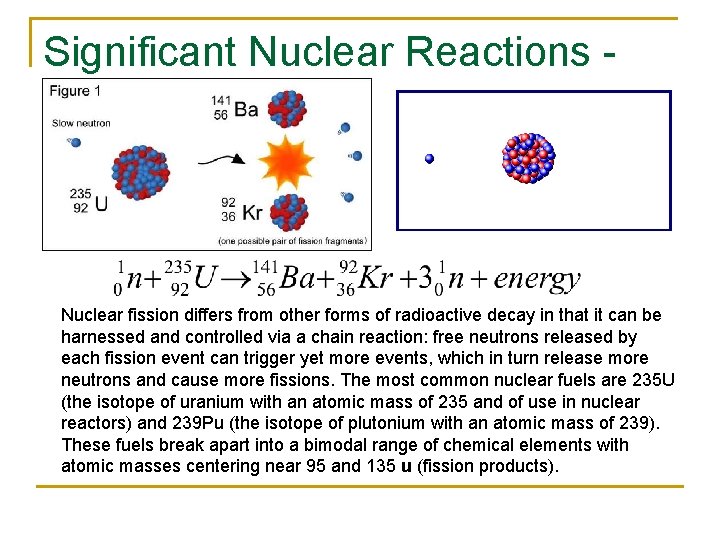
Significant Nuclear Reactions - Fission Nuclear fission differs from other forms of radioactive decay in that it can be harnessed and controlled via a chain reaction: free neutrons released by each fission event can trigger yet more events, which in turn release more neutrons and cause more fissions. The most common nuclear fuels are 235 U (the isotope of uranium with an atomic mass of 235 and of use in nuclear reactors) and 239 Pu (the isotope of plutonium with an atomic mass of 239). These fuels break apart into a bimodal range of chemical elements with atomic masses centering near 95 and 135 u (fission products).

Fission Bomb One class of nuclear weapon, a fission bomb (not to be confused with the fusion bomb), otherwise known as an atomic bomb or atom bomb, is a fission reactor designed to liberate as much energy as possible as rapidly as possible, before the released energy causes the reactor to explode (and the chain reaction to stop). A nuclear reactor is a device in which nuclear chain fission reactions are initiated, controlled, and sustained at a steady rate, as opposed to a nuclear bomb, in which the chain reaction occurs in a fraction of a second and is uncontrolled causing an explosion.

Radioactive Materials The rate of decay for radioactive substances is expressed in terms of the activity R, given by: Activity N = Number of undecayed nuclei One becquerel (Bq) is an activity equal to one disintegration per second (1 s -1). One curie (Ci) is the activity of a radioactive material that decays at the rate of 3. 7 x 1010 Bq or 3. 7 x 1010 disintegrations per second.

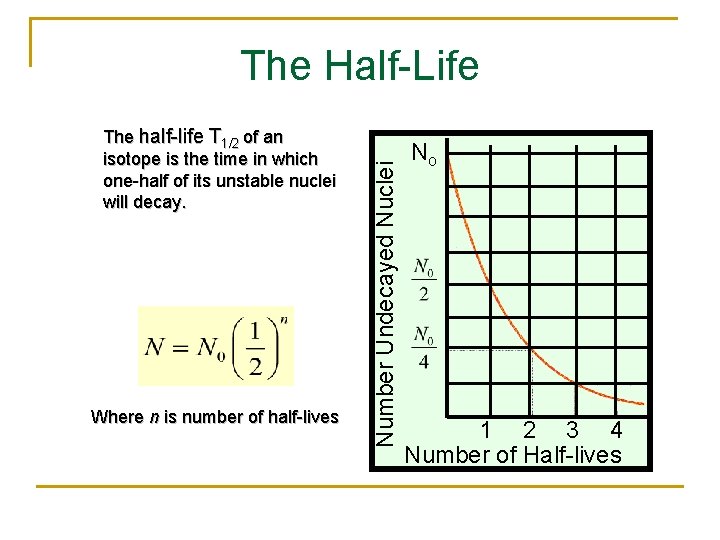
The half-life T 1/2 of an isotope is the time in which one-half of its unstable nuclei will decay. Where n is number of half-lives Number Undecayed Nuclei The Half-Life No 1 2 3 4 Number of Half-lives

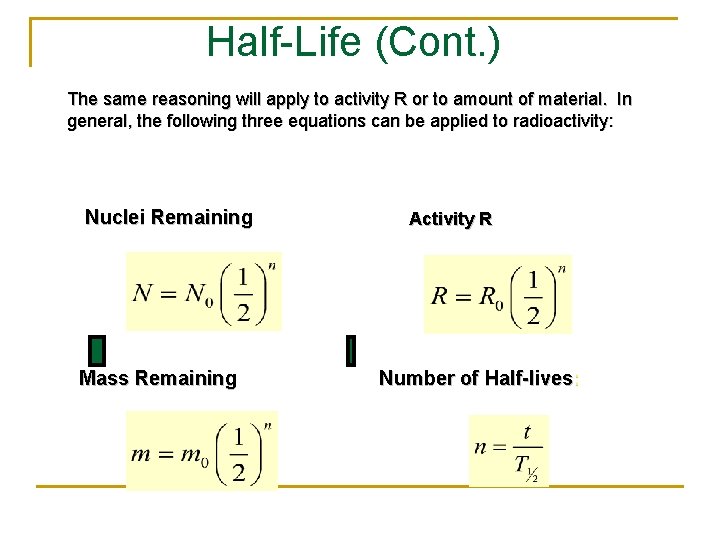
Half-Life (Cont. ) The same reasoning will apply to activity R or to amount of material. In general, the following three equations can be applied to radioactivity: Nuclei Remaining Mass Remaining Activity R Number of Half-lives:

Example 6: A sample of iodine-131 has an initial activity of 5 m. Ci. The half-life of I-131 is 8 days. What is the activity of the sample 32 days later? First we determine the number of half-lives: n = 4 half-lives R = 0. 313 m. Ci There would also be 1/16 remaining of the mass and 1/16 of the number of nuclei.

Nuclear Reactions It is possible to alter the structure of a nucleus by bombarding it with small particles. Such events are called nuclear reactions: General Reaction: x+X Y+y For example, if an alpha particle bombards a nitrogen-14 nucleus it produces a hydrogen atom and oxygen-17:

Conservation Laws For any nuclear reaction, there are three conservation laws which must be obeyed: Conservation of Charge: The total charge of a system can neither be increased nor decreased. Conservation of Nucleons: The total number of nucleons in a reaction must be unchanged. Conservation of Mass Energy: The total mass-energy of a system must not change in a nuclear reaction.

Example 7: Use conservation criteria to determine the unknown element in the following nuclear reaction: Charge before = +1 + 3 = +4 Charge after = +2 + Z = +4 Z = 4 – 2 = 2 (Helium has Z = 2) Nucleons before = 1 + 7 = 8 Nucleons after = 4 + A = 8 (Thus, A = 4)

Conservation of Mass-Energy There is always mass-energy associated with any nuclear reaction. The energy released or absorbed is called the Q-value and can be found if the atomic masses are known before and after. Q is the energy released in the reaction. If Q is positive, it is exothermic. If Q is negative, it is endothermic.

Example 8: Calculate the energy released in the bombardment of lithium-7 with hydrogen-1. Substitution of these masses gives: Q = 0. 018622 u(931. 5 Me. V/u) The positive Q means the reaction is exothermic. Q =17. 3 Me. V

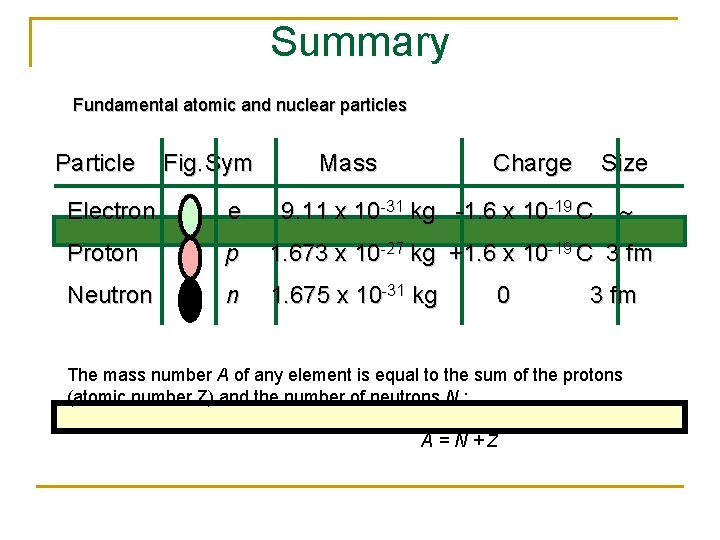
Summary Fundamental atomic and nuclear particles Particle Fig. Sym Mass Charge Size Electron e 9. 11 x 10 -31 kg -1. 6 x 10 -19 C Proton p 1. 673 x 10 -27 kg +1. 6 x 10 -19 C 3 fm Neutron n 1. 675 x 10 -31 kg 0 3 fm The mass number A of any element is equal to the sum of the protons (atomic number Z) and the number of neutrons N : A=N+Z

Summary Definitions: A nucleon is a general term to denote a nuclear particle - that is, either a proton or a neutron. The mass number A of an element is equal to the total number of nucleons (protons + neutrons). Isotopes are atoms that have the same number of protons (Z 1= Z 2), but a different number of neutrons (N). (A 1 A 2) A nuclide is an atom that has a definite mass number A and Z-number. A list of nuclides will include isotopes.

Summary (Cont. ) Symbolic notation for atoms Mass defect m. D Binding energy EB = m. Dc 2 where c 2 = 931. 5 Me. V/u Binding Energy per nucleon

Summary (Decay Particles) An alpha particle a is the nucleus of a helium atom consisting of two protons and two tightly bound neutrons. A beta-minus particle b- is simply an electron that has been expelled from the nucleus. A beta positive particle b+ is essentially an electron with positive charge. The mass and speeds are similar. A gamma ray g has very high electromagnetic radiation carrying energy away from the nucleus.

Summary (Cont. ) Alpha Decay: Beta-minus Decay: Beta-plus Decay:

Summary (Radioactivity) The half-life T 1/2 of an isotope is the time in which one-half of its unstable nuclei will decay. Nuclei Remaining Mass Remaining Activity R Number of Half-lives:

Summary (Cont. ) Nuclear Reaction: x+X Y+y+Q Conservation of Charge: The total charge of a system can neither be increased nor decreased. Conservation of Nucleons: The total number of nucleons in a reaction must be unchanged. Conservation of Mass Energy: The total mass-energy of a system must not change in a nuclear reaction. (Q-value = energy released)

CONCLUSION: Chapter 39 Nuclear Physics

Atomic Physics & Quantum Effects AP Physics B

Blackbody radiation n A blackbody absorbs all incident light rays. n All bodies, no matter how hot or cold, emit electromagnetic waves. We can see the waves emitted by very hot objects because they are within the visible spectrum (light bulb filament; red-hot metal). At lower temps we can’t see the waves but they are still there. For example, the human body emits waves in the infrared range. This is why we can use infrared detecting devices to “see” in the dark. n The distribution of energy in blackbody radiation is independent of the material from which the blackbody is constructed – it depends only on the temperature.

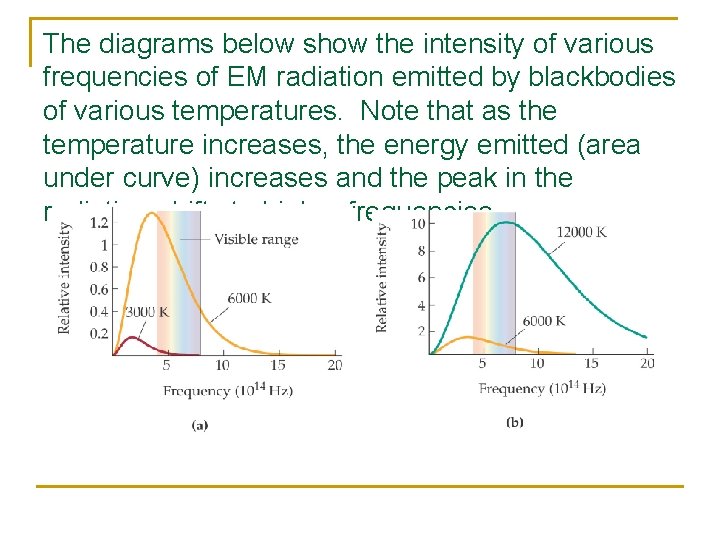
The diagrams below show the intensity of various frequencies of EM radiation emitted by blackbodies of various temperatures. Note that as the temperature increases, the energy emitted (area under curve) increases and the peak in the radiation shifts to higher frequencies.

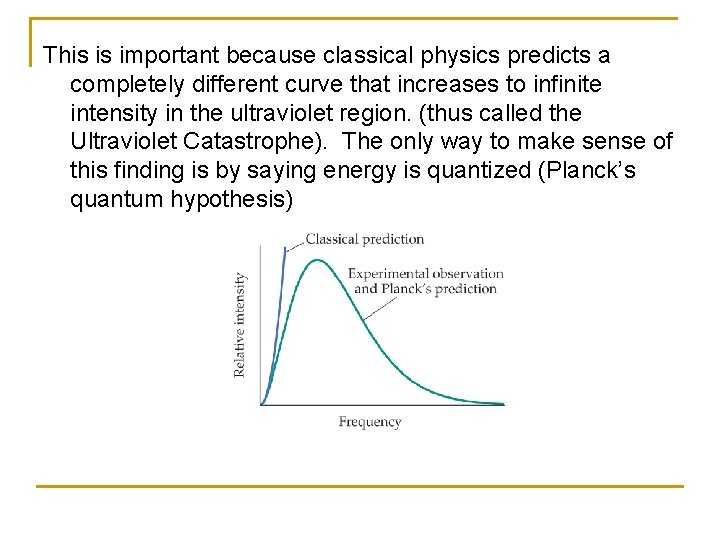
This is important because classical physics predicts a completely different curve that increases to infinite intensity in the ultraviolet region. (thus called the Ultraviolet Catastrophe). The only way to make sense of this finding is by saying energy is quantized (Planck’s quantum hypothesis)

Quantum? Quantum mechanics is the study of processes which occur at the atomic scale. The word "quantum" is derived From Latin to mean BUNDLE. Therefore, we are studying the motion of objects that come in small bundles called quanta. These tiny bundles that we are referring to are electrons traveling around the nucleus.

“Newton, forgive me. . ”, Albert At the atomic scale Newtonian Mechanics Einstein cannot seem to describe the motion of particles. An electron trajectory between two points for example IS NOT a perfect parabolic trajectory as Newton's Laws predicts. Where Newton's Laws end Quantum Mechanics takes over. . . IN A BIG WAY! One of the most popular concepts concerning Quantum Mechanics is called , “The Photoelectric Effect”. In 1905, Albert Einstein published this theory for which he won the Nobel Prize in 1921.

What is the Photoelectric Effect? In very basic terms, it is when electrons are released from a certain type of metal upon receiving enough energy from incident light. So basically, light comes down and strikes the metal. If the energy of the light wave is sufficient, the electron will then shoot out of the metal with some velocity and kinetic energy.

The Electron-Volt = ENERGY Before we begin to discuss the photoelectric effect, we must introduce a new type of unit. Recall: This is a very useful unit as it shortens our calculations and allows us to stray away from using exponents.

The Photoelectric Effect "When light strikes a material, electrons are emitted. The radiant energy supplies the work necessary to free the electrons from the surface. "

Photoelectric Fact #1 The LIGHT ENERGY (E) is in the form of quanta called PHOTONS. Since light is an electromagnetic wave it has an oscillating electric field. The more intense the light the more the field oscillates. In other words, its frequency is greater.

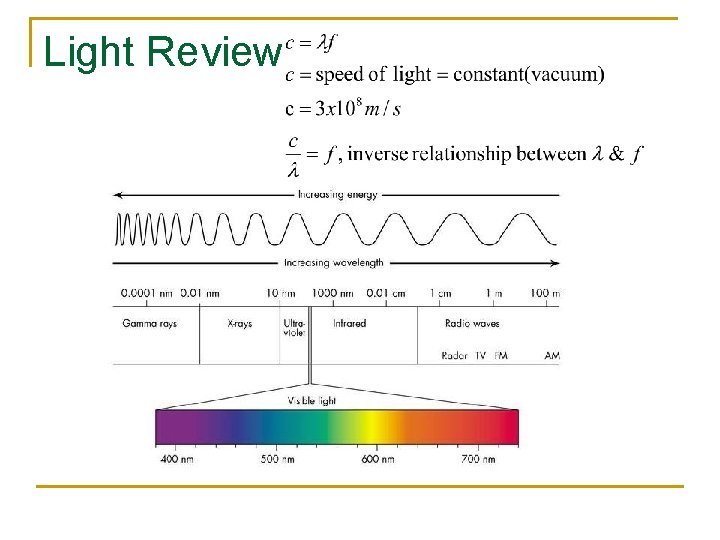
Light Review

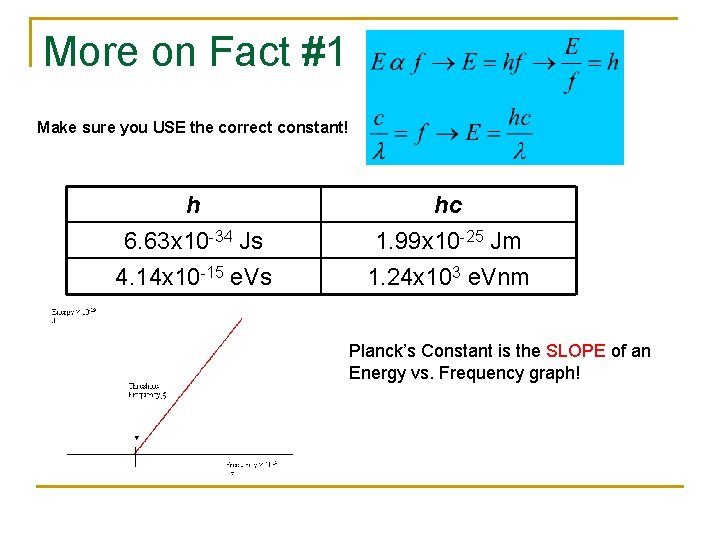
More on Fact #1 Make sure you USE the correct constant! h 6. 63 x 10 -34 Js 4. 14 x 10 -15 e. Vs hc 1. 99 x 10 -25 Jm 1. 24 x 103 e. Vnm Planck’s Constant is the SLOPE of an Energy vs. Frequency graph!

Photoelectric Fact #2 The frequency of radiation must be above a certain value before the energy is enough. This minimum frequency required by the source of electromagnetic radiation to just liberate electrons from the metal is known as threshold frequency, f 0. The threshold frequency is the X-intercept of the Energy vs. Frequency graph!

Photoelectric Fact #3 Work function, f, is defined as the least energy that must be supplied to remove a free electron from the surface of the metal, against the attractive forces of surrounding positive ions. Shown here is a PHOTOCELL. When incident light of appropriate frequency strikes the metal (cathode), the light supplies energy to the electron. The energy need to remove the electron from the surface is the WORK! Not ALL of the energy goes into work! As you can see the electron then MOVES across the GAP to the anode with a certain speed and kinetic energy.

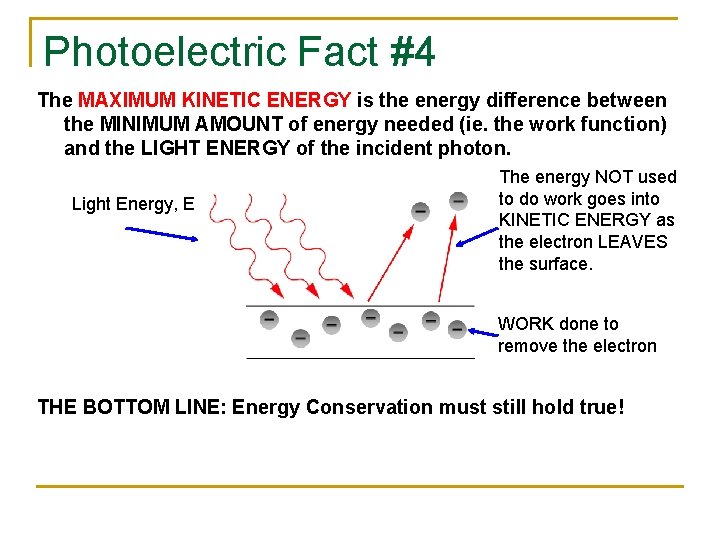
Photoelectric Fact #4 The MAXIMUM KINETIC ENERGY is the energy difference between the MINIMUM AMOUNT of energy needed (ie. the work function) and the LIGHT ENERGY of the incident photon. Light Energy, E The energy NOT used to do work goes into KINETIC ENERGY as the electron LEAVES the surface. WORK done to remove the electron THE BOTTOM LINE: Energy Conservation must still hold true!

Putting it all together KINETIC ENERGY can be plotted on the y axis and FREQUENCY on the xaxis. The WORK FUNCTION is the y – intercept as the THRESHOLD FREQUNECY is the x intercept. PLANCK‘S CONSTANT is the slope of the graph.

Can we use this idea in a circuit? We can then use this photoelectric effect idea to create a circuit using incident light. Of course, we now realize that the frequency of light must be of a minimum frequency for this work. Notice the + and – on the photocell itself. We recognize this as being a POTENTIAL DIFFERENCE or Voltage. This difference in voltage is represented as a GAP that the electron has to jump so that the circuit works What is the GAP or POTENTIAL DIFFERENCE is too large?

Photoelectric Fact #5 - Stopping If the voltage is TOO LARGE the electrons WILL NOT have Potential enough energy to jump the gap. We call this VOLTAGE point the STOPPING POTENTIAL. If the voltage exceeds this value, no photons will be emitted no matter how intense. Therefore it appears that the voltage has all the control over whether the photon will be emitted and thus has kinetic energy.

Importance of photoelectric effect: n Classical physics predicts that any frequency of light can eject electrons as long as the intensity is high enough. n Experimental data shows there is a minimum (cutoff frequency) that the light must have. n Classical physics predicts that the kinetic energy of the ejected electrons should increase with the intensity of the light. n Again, experimental data shows this is not the case; increasing the intensity of the light only increases the number of electrons emitted, not their kinetic energy. n THUS the photoelectric effect is strong evidence for the photon model of light.

Wave-Particle Duality The results of the photoelectric effect allowed us to look at light completely different. First we have Thomas Young’s Diffraction experiment proving that light behaved as a WAVE due to constructive and destructive interference. Then we have Max Planck who allowed Einstein to build his photoelectric effect idea around the concept that light is composed of PARTICLES called quanta.

The momentum of the photon n n Combining E=mc 2 and p=mv, you get: p / E = v / c 2 The photon travels at the speed of light, so v = c and p / E = 1 / c n n Therefore the momentum, p, of the photon is p = E / c But we also know that E = hf and λ=c/f, so

This led to new questions…. If light is a WAVE and is ALSO a particle, does that mean ALL MATTER behave as waves? That was the question that Louis de Broglie pondered. He used Einstein's famous equation to answer this question.

YOU are a matter WAVE! Basically all matter could be said to have a momentum as it moves. The momentum however is inversely proportional to the wavelength. So since your momentum would be large normally, your wavelength would be too small to measure for any practical purposes. An electron, however, due to it’s mass, would have a very small momentum relative to a person and thus a large enough wavelength to measure thus producing measurable results. This led us to start using the Electron Microscopes rather than traditional Light microscopes.

The electron microscope After the specimen is prepped. It is blasted by a bean of electrons. As the incident electrons strike the surface, electrons are released from the surface of the specimen. The de. Broglie wavelength of these released electrons vary in wavelength which can then be converted to a signal by which a 3 D picture can then be created based on the signals captured by the detector.

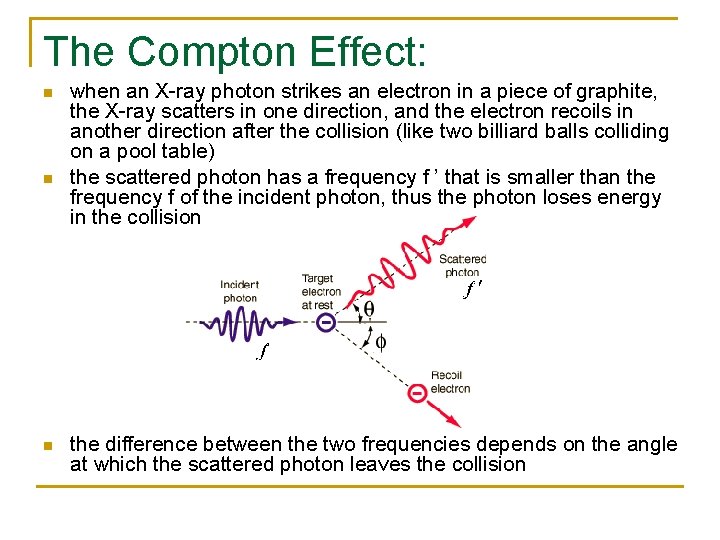
The Compton Effect: n n n when an X-ray photon strikes an electron in a piece of graphite, the X-ray scatters in one direction, and the electron recoils in another direction after the collision (like two billiard balls colliding on a pool table) the scattered photon has a frequency f ’ that is smaller than the frequency f of the incident photon, thus the photon loses energy in the collision the difference between the two frequencies depends on the angle at which the scattered photon leaves the collision

Similar to the analysis for the kinetic energy and work for photoelectric effect, we find: q The electron is assumed to be initially at rest and essentially free (not bound to the atoms of the material) q According to principle of conservation of energy: hf = hf ’ + K or energy of incident photon = energy of scattered photon + KE of en n For an initially stationary electron, conservation of total linear momentum requires that: q Momentum of incident photon = momentum of scattered photon + momentum of electron n From this point, these equations are combined with the relativistic equations for energy and momentum to derive the equation for Compton Scattering.

n The difference between the wavelength λ’ of the scattered photon and the wavelength λ of the incident photon is related to the scattering angle θ by: q m is the mass of the electron. h/mc is the “Compton wavelength of the electron” and is h/mc = 2. 43 x 10 -12 m. It is interesting to note that according to Einstein’s theory of relativity, the rest mass of a photon is zero. However, it is never at rest, it is always moving (at the speed of light!) so it does have a finite momentum (even though p=mv doesn’t work)

The Davisson-Germer experiment demonstrated the wave nature of the electron, confirming the earlier hypothesis of de. Broglie. n Davisson and Germer measured the energies of electrons scattering from a metal surface. Electrons from a heated filament were accelerated by a voltage and allowed to strike the surface of nickel metal, which could be rotated to observe angular dependence of the scattered electrons. They found that at certain angles there was a peak in the intensity of the scattered electron beam. In fact, the electron beam was scattered by the surface atoms on the nickel at the exact angles predicted for the diffraction of x-rays according to Bragg's formula nλ=2 dsinθ, with a wavelength given by the de Broglie equation, λ=h/p. X-rays are accepted to be wavelike, thus this is evidence for wavelike behavior of electron.

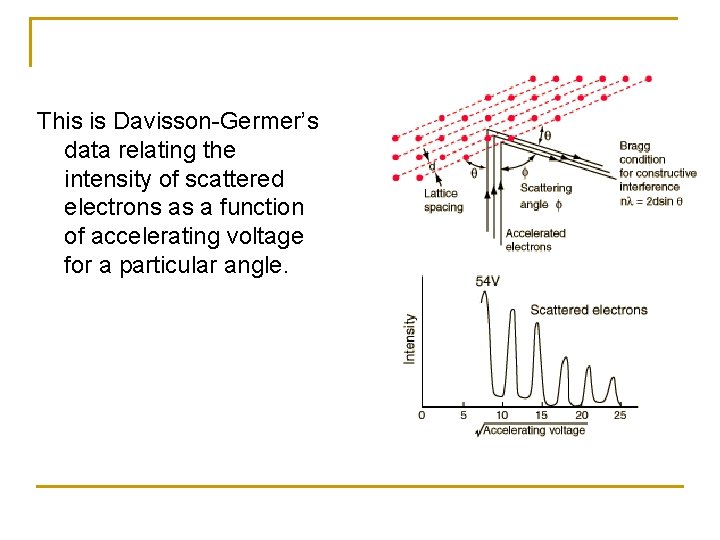
This is Davisson-Germer’s data relating the intensity of scattered electrons as a function of accelerating voltage for a particular angle.

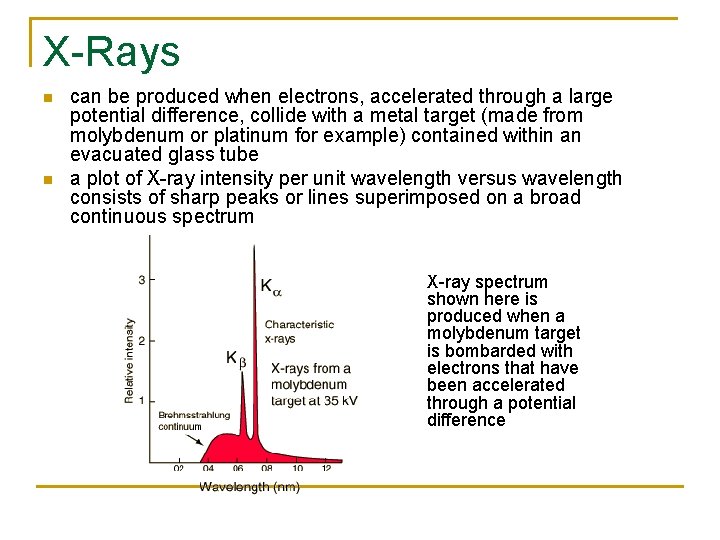
X-Rays n n can be produced when electrons, accelerated through a large potential difference, collide with a metal target (made from molybdenum or platinum for example) contained within an evacuated glass tube a plot of X-ray intensity per unit wavelength versus wavelength consists of sharp peaks or lines superimposed on a broad continuous spectrum X-ray spectrum shown here is produced when a molybdenum target is bombarded with electrons that have been accelerated through a potential difference

n n n n when the energetic electrons impact the target metal, they undergo a rapid deceleration (braking). as the electrons suddenly come to rest they give off high -energy radiation in the form of X-rays over a wide range of wavelengths. This is referred to as “Bremsstrahlung continuum” (bremsstrahlung is German for “braking radiation”) This is the base for the peaks seen in the graph the sharp peaks are called characteristic lines or characteristic X-rays because they are characteristic of the target material. the characteristic lines are marked Kα and Kβ because they involve the n=1 or K shell of a metal atom. (K shell is the innermost electron shell) if an electron with enough energy strikes the target, one of the K-shell electrons can be knocked entirely out of a target atom an electron in one of the outer shells can then fall into the K shell, and an X-ray photon is emitted in the process. Kα is a change from n=2 to n=1; Kβ is a change from n=3 to n=1 there is a cutoff wavelength (as seen in the diagram). an impinging electron cannot give up any more than all of its KE, thus an emitted X-ray photon can have an energy no more than the KE of the impinging electron. the wavelength that corresponds to this is the cutoff wavelength (max frequency-min wavelength). K=e. V, E=hf thus e. V=hf. f=c/λ, so… V is the potential difference applied across the X-ray tube; e is the charge of an electron

Line Spectra n n n for a solid object the radiation emitted has a continuous range of wavelengths, some of which are in the visible region of the spectrum. the continuous range of wavelengths is characteristic of the entire collection of atoms that make up the solid. in contrast, individual atoms, free of the strong interactions that are present in a solid, emit only certain specific wavelengths, rather than a continuous range. these wavelengths are characteristic of the atom. q a low-pressure gas in a sealed tube can be made to emit EM waves by applying a sufficiently large potential difference between two electrodes located within the tube q with a grating spectroscope the individual wavelengths emitted by the gas can be separated and identified as a series of bright fringes or lines. these series of lines are called the LINE SPECTRA.

Bohr Model of Hydrogen atom n n Bohr tried to derive the formula that describes the line spectra that was developed by Balmer using trial and error. he used Rutherford’s model of the atom, the quantum ideas of Planck and Einstein, and the traditional description of a particle in uniform circular motion. assumptions of Bohr model: q q n electron in H moves in circular motion only orbits where the angular momentum of the electron is equal to an integer times Planck’s constant divided by 2π are allowed electrons in allowed orbits do not radiate EM waves. Thus the orbits are stable. (if it emitted radiation, it would lose energy and spiral into the nucleus) EM radiation is given off or absorbed only when an electron changes from one allowed orbit to another. ΔE = hf (ΔE is energy difference between orbits and f is frequency of radiation emitted or absorbed) Bohr theorized that a photon is emitted only when the electron changes orbits from a larger one with a higher energy to a smaller one with a lower energy.

Bohr Energy levels in electron the centripetal force that provides the circular orbit is electrostatic force (Coulomb’s Law). setting this equal to centripetal force we get: volts n or note that electrostatic force between an electron and a nucleus with Z protons is ke(Ze)/r 2 = k. Ze 2/r 2. (Z = # of protons = atomic number) n angular momentum is L=rmv. the second assumption listed above states the angular momentum of a given orbit, Ln, equals an integar, n, times h/2π; or Ln=nh/2π. setting these equal and solving for v gives: n combining these two equations gives: (note that n is the orbital number) n solving for rn gives us Bohr orbital radius

n n energy of electron is sum of kinetic and potential energies: E = K + U = ½ mv 2 + U the electrostatic potential energy is U = -k. Ze 2/r and using the first equation in this section we get: n substituting in the Bohr orbital radius, rn, from above: n grouping all of the constants yields: n plugging in values for the constants gives us: Z = atomic number; n = energy level (1, 2, 3, …)

n n when an electron in an initial orbit with a larger energy Ei, drops to a lower orbit with energy Ef, the emitted photon has an energy of Ei – Ef , consistent with the law of conservation of energy. combining this with Einstein’s E = hf, we get Ei – Ef = hf To find the wavelengths in hydrogen’s line spectrum (Z=1), we apply that to the equation above: n given that E = hc/λ : n the value in the first parenthesis is only constants. calculating this value gives the Rydberg Constant (1. 097 x 107) – the exact value that Balmer found

de Broglie Waves and Bohr the angular momentum assumption in Bohr’s model is there because it Model produces results in agreement with experiment. n n n however, de Broglie matter-wave relationship explains the significance: think of matter (electron) waves as analogous to a wave on a string – except that the string is a circle representing the electrons orbit. the standing wave must fit an integral number of wavelengths into the circumference of the orbit: nλ=2πr. combine this with p=h/λ: n rearranging and multiplying both sides of the equation by r gives us angular momentum n Thus this condition of the Bohr model is a reflection of the wave nature of matter

Life and Atoms Every time you breathe you are taking in atoms. Oxygen atoms to be exact. These atoms react with the blood and are carried to every cell in your body for various reactions you need to survive. Likewise, every time you breathe out carbon dioxide atoms are released. The cycle here is interesting. TAKING SOMETHING IN. ALLOWING SOMETHING OUT!

The Atom As you probably already know an atom is the building block of all matter. It has a nucleus with protons and neutrons and an electron cloud outside of the nucleus where electrons are orbiting and MOVING. Depending on the ELEMENT, the amount of electrons differs as well as the amounts of orbits surrounding the atom.

When the atom gets excited or NOT To help visualize the atom think of it like a ladder. The bottom of the ladder is called GROUND STATE where all electrons would like to exist. If energy is ABSORBED it moves to a new rung on the ladder or ENERGY LEVEL called an EXCITED STATE. This state is AWAY from the nucleus. As energy is RELEASED the electron can relax by moving to a new energy level or rung down the ladder.

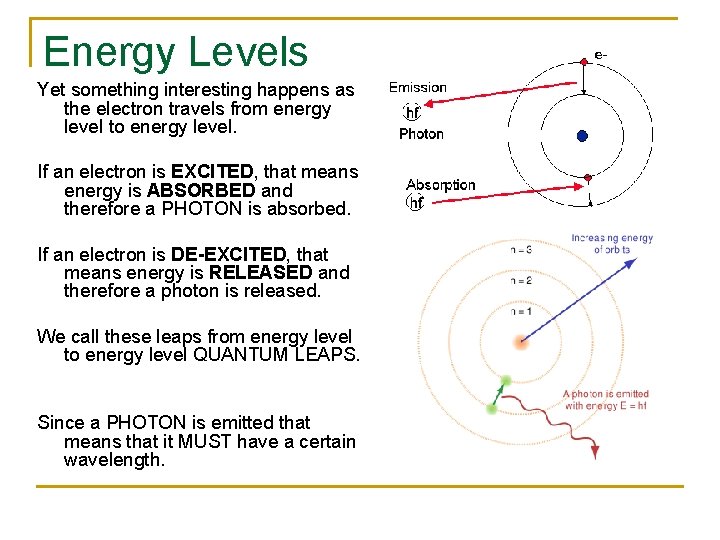
Energy Levels Yet something interesting happens as the electron travels from energy level to energy level. If an electron is EXCITED, that means energy is ABSORBED and therefore a PHOTON is absorbed. If an electron is DE-EXCITED, that means energy is RELEASED and therefore a photon is released. We call these leaps from energy level to energy level QUANTUM LEAPS. Since a PHOTON is emitted that means that it MUST have a certain wavelength.

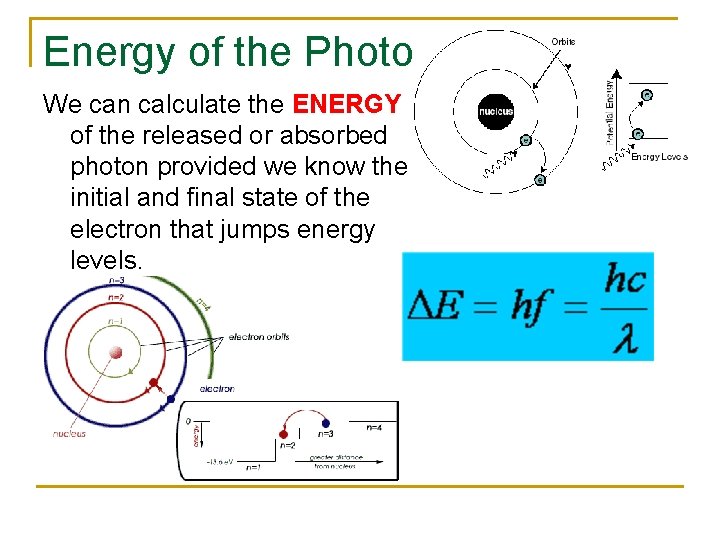
Energy of the Photon We can calculate the ENERGY of the released or absorbed photon provided we know the initial and final state of the electron that jumps energy levels.

Energy Level Diagrams. To represent these transitions we can construct an ENERGY LEVEL DIAGRAM Note: It is very important to understanding that these transitions DO NOT have to occur as a single jump! It might make TWO JUMPS to get back to ground state. If that is the case, TWO photons will be emitted, each with a different wavelength and energy.

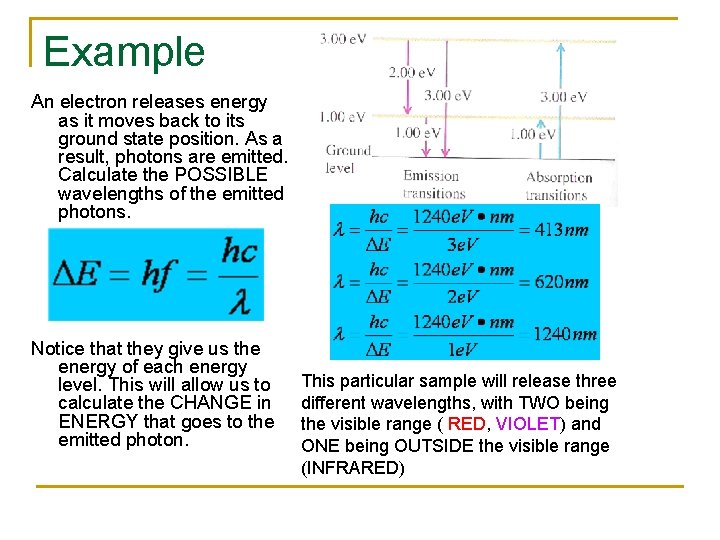
Example An electron releases energy as it moves back to its ground state position. As a result, photons are emitted. Calculate the POSSIBLE wavelengths of the emitted photons. Notice that they give us the energy of each energy level. This will allow us to calculate the CHANGE in ENERGY that goes to the emitted photon. This particular sample will release three different wavelengths, with TWO being the visible range ( RED, VIOLET) and ONE being OUTSIDE the visible range (INFRARED)

Energy levels Application: Spectroscopy is an optical technique by which we can IDENTIFY a material based on its emission spectrum. It is heavily used in Astronomy and Remote Sensing. There are too many subcategories to mention here but the one you are probably the most familiar with are flame tests. When an electron gets excited inside a SPECIFIC ELEMENT, the electron releases a photon. This photon’s wavelength corresponds to the energy level jump and can be used to indentify the element.

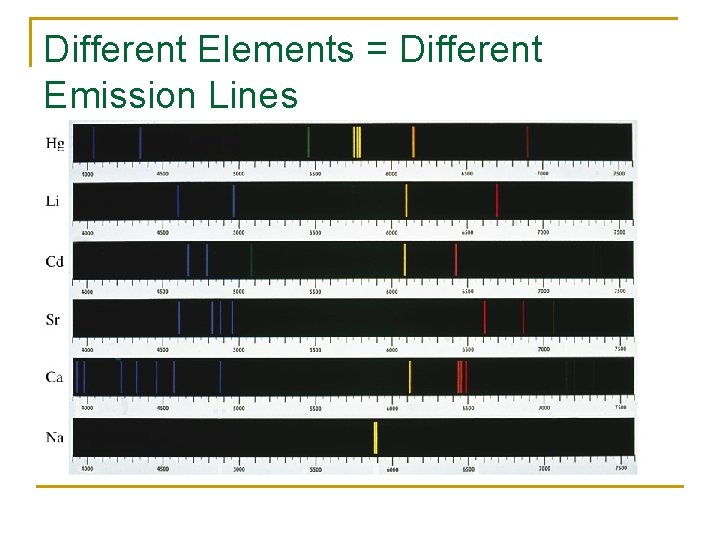
Different Elements = Different Emission Lines

Emission Line Spectra So basically you could look at light from any element of which the electrons emit photons. If you look at the light with a diffraction grating the lines will appear as sharp spectral lines occurring at specific energies and specific wavelengths. This phenomenon allows us to analyze the atmosphere of planets or galaxies simply by looking at the light being emitted from them.

Line Spectra of Hydrogen Atom n n Lyman series occurs when electrons make transition s from higher energy levels with ni = 2, 3, 4, … to the first energy level where nf = 1. notice when an electron transitions from n=2 to n=1, the longest wavelength photon in the Lyman series is emitted, since the energy change is the smallest possible. when the electron transitions from highest to lowest, the shortest wavelength is emitted.