Quantum Information Science QIS Quantum Computer The Quantum

Quantum Information Science QIS Quantum Computer

The Quantum Century

Y(1. 9)K Y 2 K Planck Shor

Three Great Ideas!

(1) Quantum Computation Feynman ‘ 81 Deutsch ‘ 85 Shor ‘ 94

A computer that operates on quantum states can perform tasks that are beyond the capability of any conceivable classical computer. Feynman ‘ 81 Deutsch ‘ 85 Shor ‘ 94

Finding Prime Factors 1807082088687 4048059516561 6440590556627 8102516769401 3491701270214 5005666254024 4048387341127 5908123033717 8188796656318 2013214880557 = ? ´ ?

Finding Prime Factors 1807082088687 4048059516561 6440590556627 8102516769401 3491701270214 5005666254024 4048387341127 5908123033717 8188796656318 2013214880557 = 3968599945959 7454290161126 1628837860675 7644911281006 4832555157243 ´ 4553449864673 5972188403686 8972744088643 5630126320506 9600999044599 Shor ‘ 94

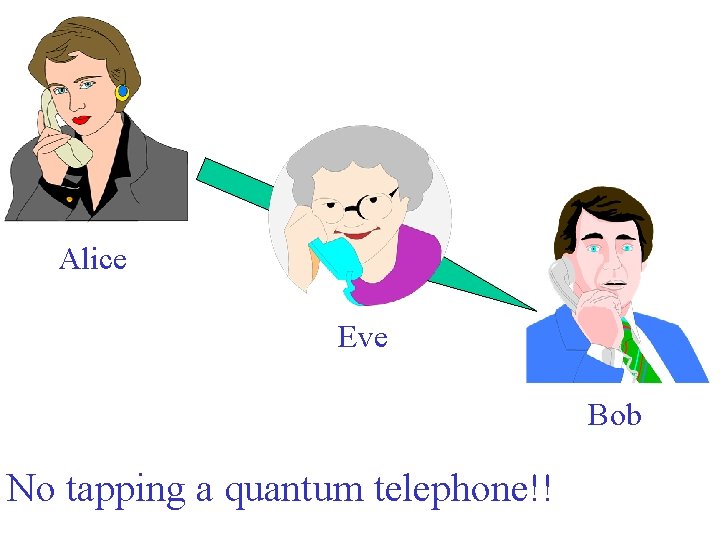
(2) Quantum Key Distribution Bennett Brassard ‘ 84

Eavesdropping on quantum information can be detected; key distribution via quantum states is unconditionally secure. Bennett Brassard ‘ 84

Alice Eve Bob No tapping a quantum telephone!!

(3) Quantum Error Correction Shor ‘ 95 Steane ‘ 95

Quantum information can be protected, and processed fault-tolerantly. Shor ‘ 95 Steane ‘ 95

Quantum Error Correction

Quantum Error Correction Error!

Quantum Error Correction

Quantum Error Correction Redundancy protects against quantum errors!

Three Great Ideas: 1) Quantum Computation 2) Quantum Key Distribution 3) Quantum Error Correction Where will they lead? Challenges for 21 st century science!

Quantum information and precision measurement LIGO III: Beyond the standard quantum limit in 2008? ! Thorne Caves Kimble

Quantum Information and Precision Measurement New strategies for the physics lab, exploiting: • quantum entanglement • quantum information processing • quantum error correction • etc.

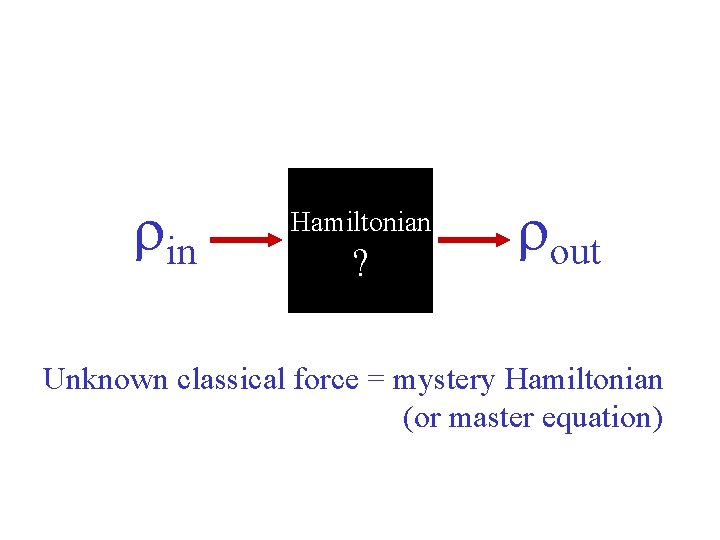
rin Hamiltonian ? rout Unknown classical force = mystery Hamiltonian (or master equation)

Hamiltonian ? rout

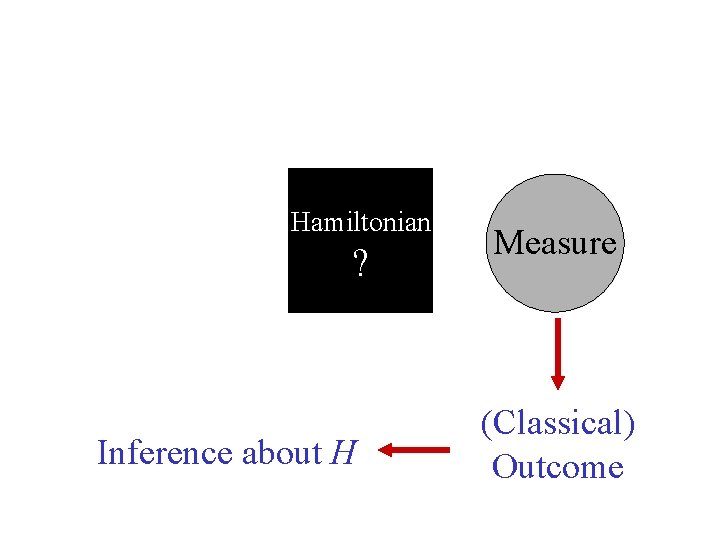
Hamiltonian ? Inference about H Measure (Classical) Outcome

rin Hamiltonian ? rout How should we “query” the box to extract “optimal” information?

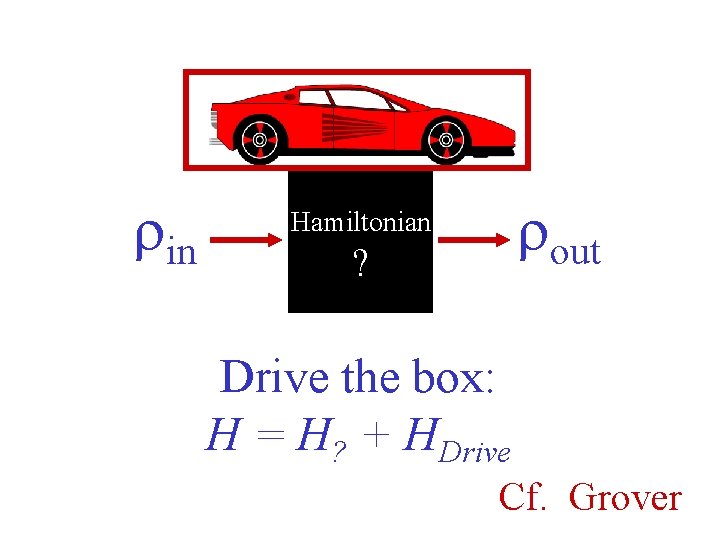
rin rout Hamiltonian ? Drive the box: H = H? + HDrive Cf. Grover

Entangled Strategies Gather More Information Which way does the spin point? Bloch sphere

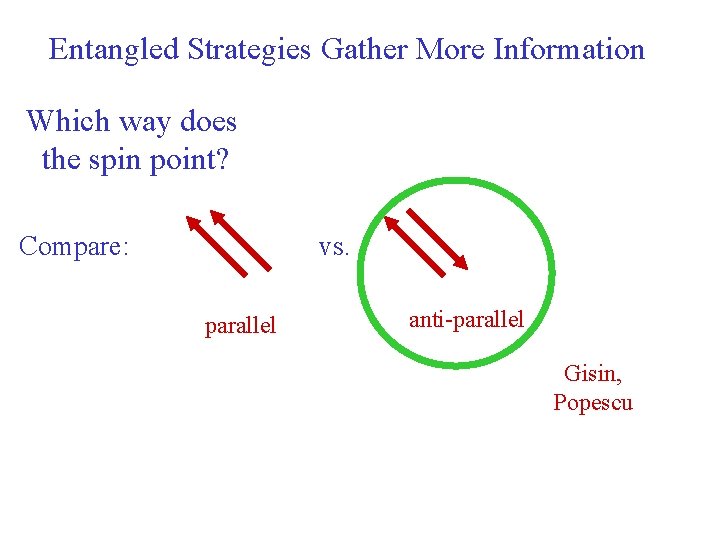
Entangled Strategies Gather More Information Which way does the spin point? Compare: vs. parallel anti-parallel Gisin, Popescu

Ion Trap Quantum Computer I. Cirac, P. Zoller

Ion Trap Quantum Computer I. Cirac, P. Zoller

Ion Trap Quantum Computer I. Cirac, P. Zoller

Ion Trap Quantum Computer I. Cirac, P. Zoller

Ion Trap Quantum Computer I. Cirac, P. Zoller

Experimental Challenges: • Read out single qubits. • Controlled coherent multi-qubit interactions. • Controlled fabrication. • etc. From ions, photons, atoms to nuclei, electrons. What quantum states and operations are useful and/or important?

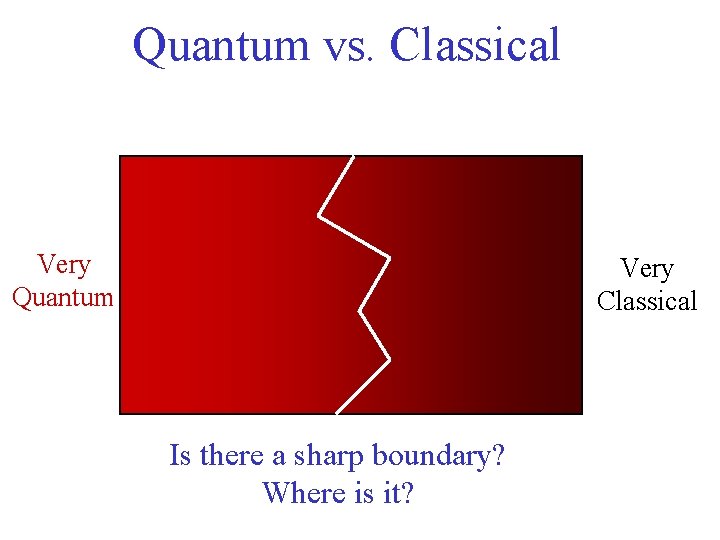
Quantum vs. Classical Very Quantum Very Classical Is there a sharp boundary? Where is it?

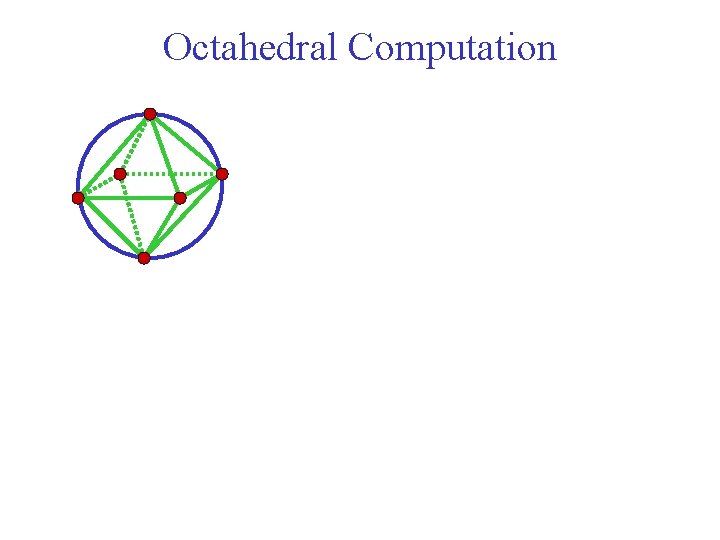
Octahedral Computation Bloch Sphere

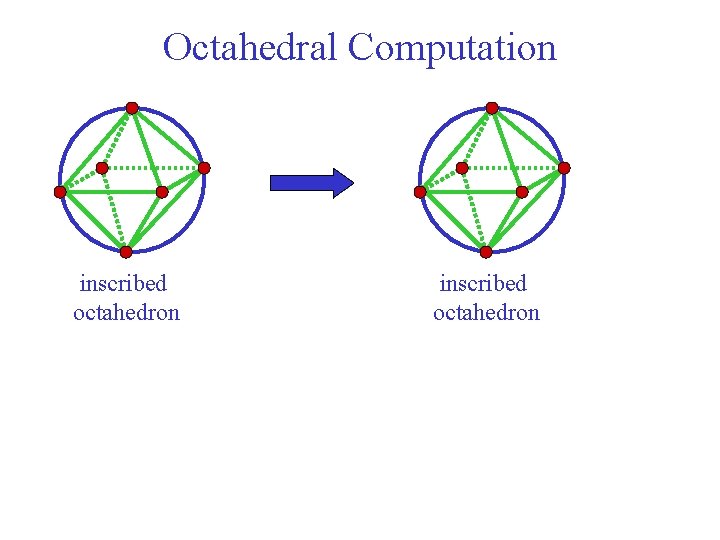
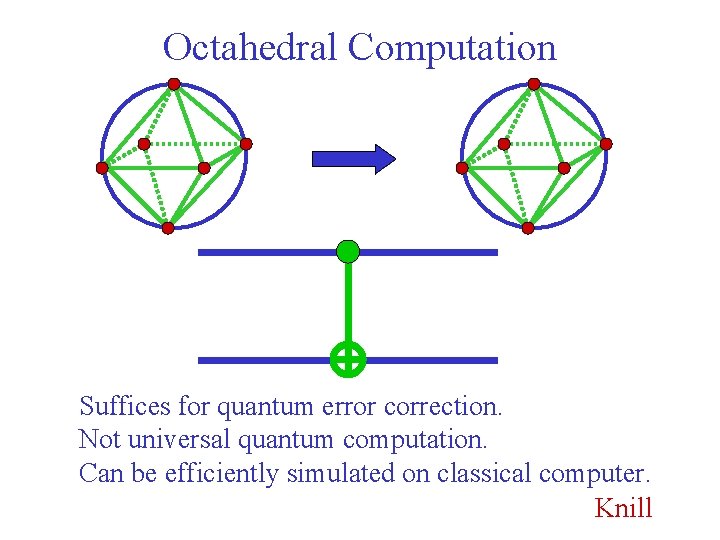
Octahedral Computation inscribed octahedron

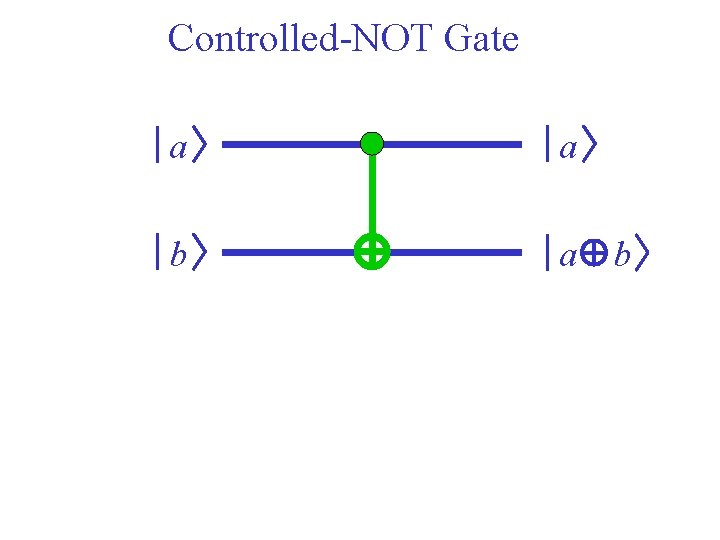
Controlled-NOT Gate a a b

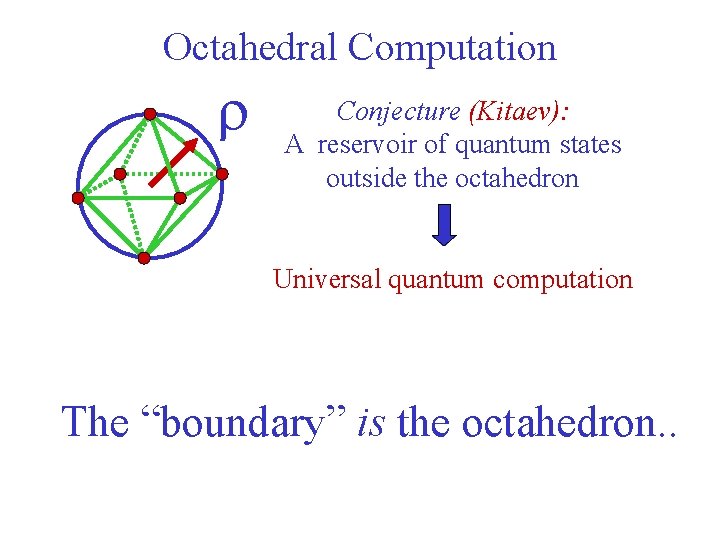
Octahedral Computation Suffices for quantum error correction. Not universal quantum computation. Can be efficiently simulated on classical computer. Knill

Octahedral Computation

Octahedral Computation r Conjecture (Kitaev): A reservoir of quantum states outside the octahedron Universal quantum computation The “boundary” is the octahedron. .

Quantum vs. Classical Very Quantum Very Classical Is there a sharp boundary? Where is it?

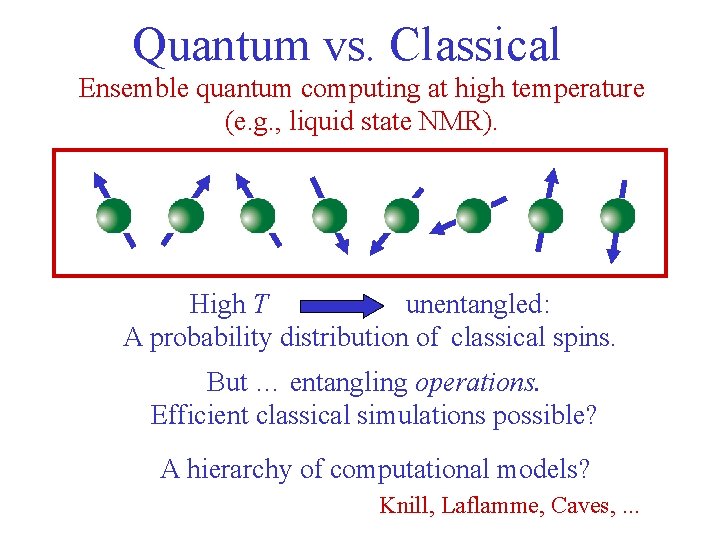
Quantum vs. Classical Ensemble quantum computing at high temperature (e. g. , liquid state NMR). High T unentangled: A probability distribution of classical spins. But … entangling operations. Efficient classical simulations possible? A hierarchy of computational models? Knill, Laflamme, Caves, . . .

Multiparticle Entanglement How to characterize it and quantify it, for pure states. Cf. , two qubits: A Y AB B

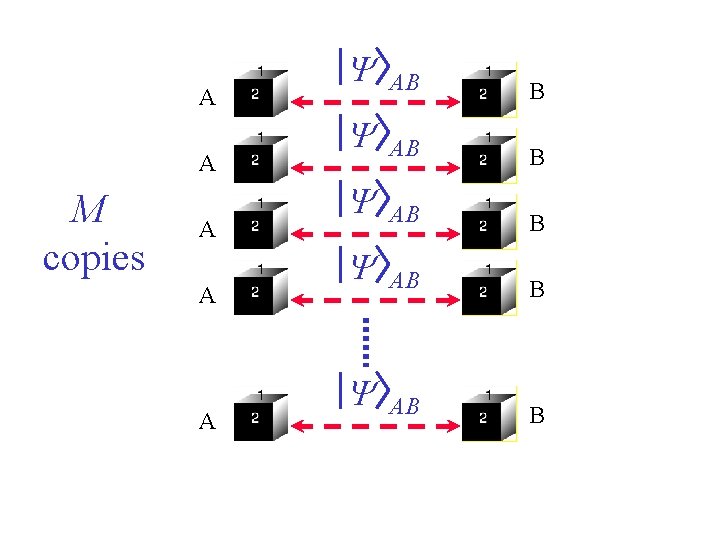
A A M copies A A A Y AB B Y AB B

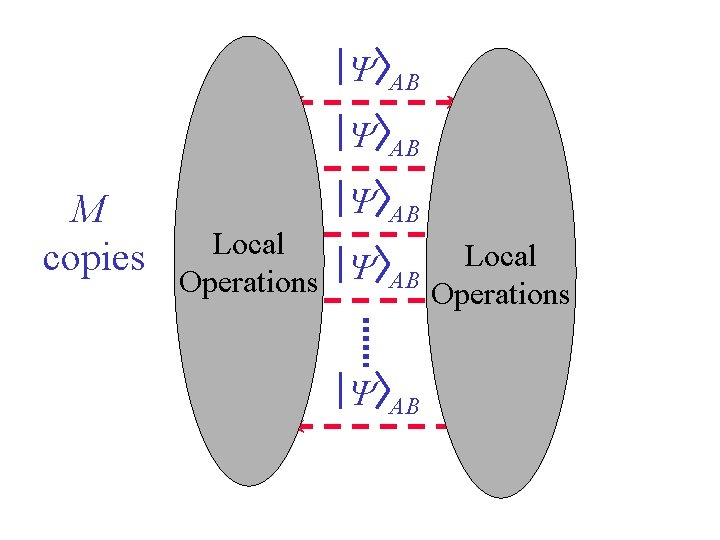
A A M copies A Y AB B Local Y Operations A A Y AB AB Local B Operations B

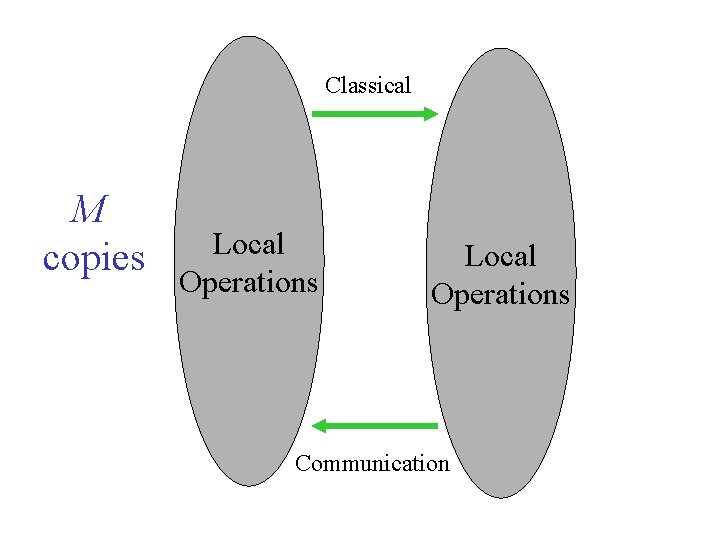
Classical M copies Local Operations Communication

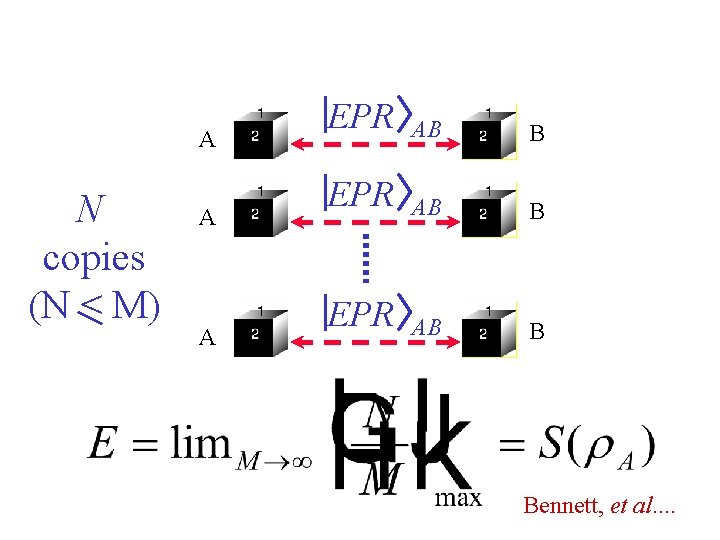
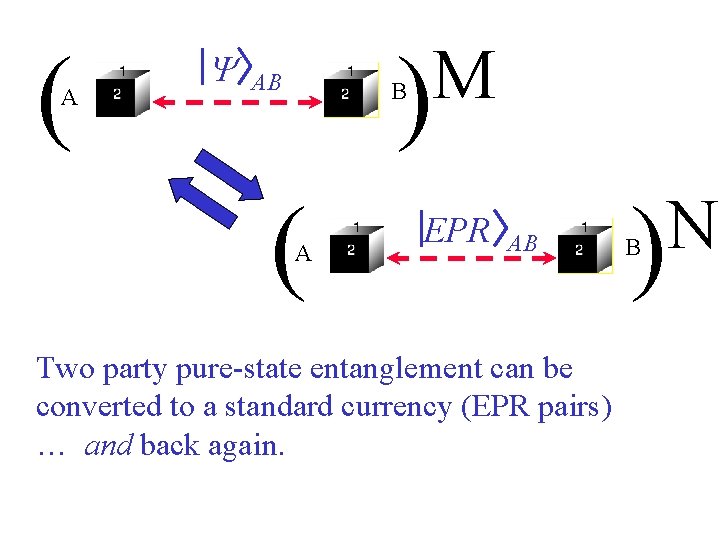
A N copies (N < M) A A EPR AB B Bennett, et al. .

( A Y M ) AB B ( A EPR AB Two party pure-state entanglement can be converted to a standard currency (EPR pairs) … and back again. N ) B

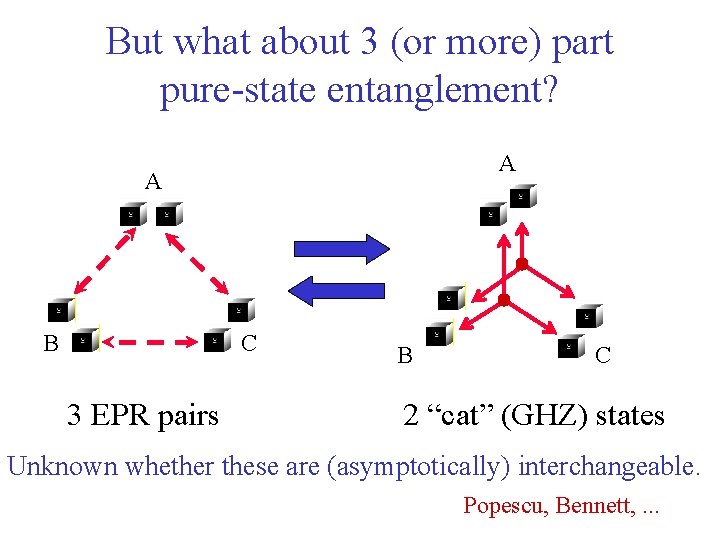
But what about 3 (or more) part pure-state entanglement? A A B C 3 EPR pairs B C 2 “cat” (GHZ) states Unknown whether these are (asymptotically) interchangeable. Popescu, Bennett, . . .

Many particles 1 2 3 4 m ? Standard form: m-cats (m-1)-cats (m-2)-cats 2 -cats Quantum critical phenomena: how entangled is the ground state? Quantum dynamics: how hard to simulate (classically)?

Fermilab 103 Ge. V 1019 Ge. V !? Planckatron 1016 in energy, 1032 in luminosity. .

Feynmanlab Q

‘t Hooft Using quantum mechanics, a device can be built that can handle information in a way no classical machine will be able to reproduce, such as the determination of the prime factors of very large numbers in an amount of time not much more than what is needed to do multiplications and other basic arithmetic with these large numbers. If our theory is right, it should be possible to mimick such a device using a classical theory. This gives us a falsifiable prediction: It will never be possible to construct a `quantum computer’ that can factor a large number faster, and within a smaller region of space, than a classical machine would do, if the latter could be built out of parts at least as large and as slow as the Planckian dimensions.

Weinberg This theoretical failure to find a plausible alternative to quantum mechanics … suggests to me that quantum mechanics is the way it is because any small changes in quantum mechanics would lead to absurdities.

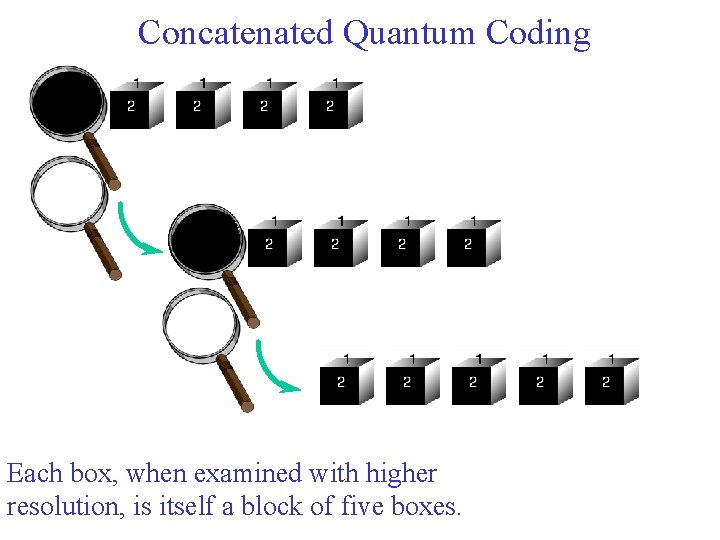
Concatenated Quantum Coding Each box, when examined with higher resolution, is itself a block of five boxes.

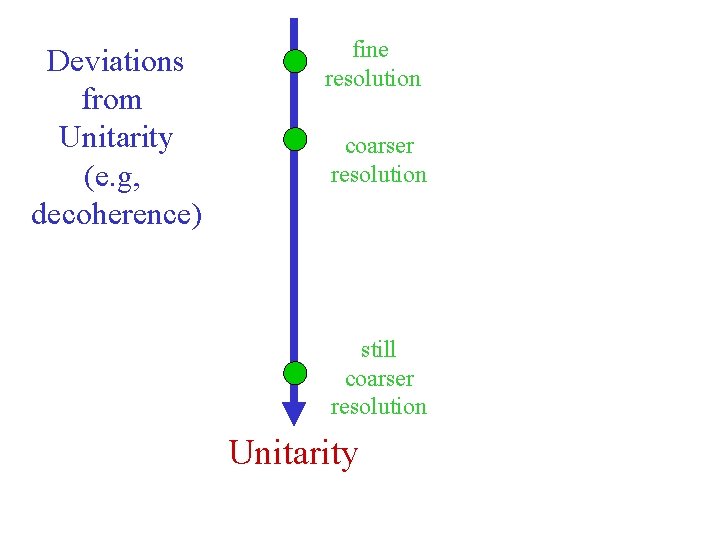
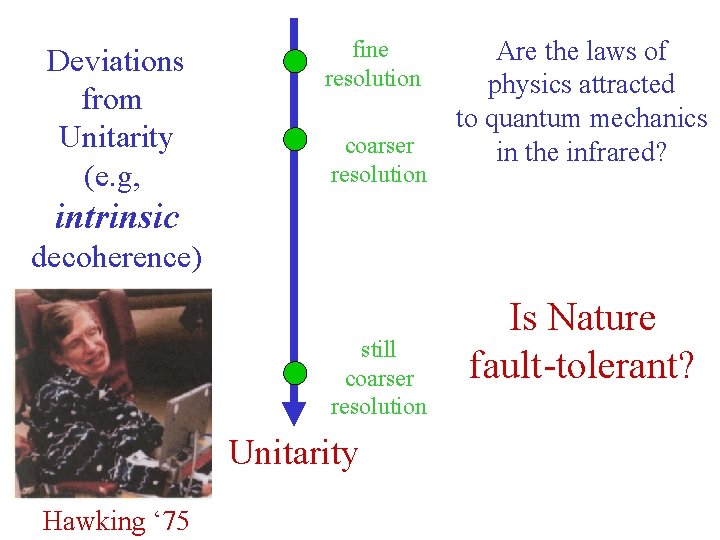
Deviations from Unitarity (e. g, decoherence) fine resolution coarser resolution still coarser resolution Unitarity

Deviations from Unitarity (e. g, fine resolution coarser resolution Are the laws of physics attracted to quantum mechanics in the infrared? intrinsic decoherence) still coarser resolution Unitarity Hawking ‘ 75 Is Nature fault-tolerant?

The 1 st Quantum Century: What happened after 1926? We learned more about the Hamiltonian of the world: Standard model, M-theory (? ) … We learned new tools for inferring its consequences: Renormalization group, broken symmetries. . and …. We began to appreciate the implications of the tensor product structure of Hilbert space: Quantum algorithms, Quantum error correction, . . .

Quantum Information Science … is much more than a faster way to factor! An enduring place at the core of computer science: Cryptography Computational complexity Communication complexity Error correction, fault-tolerance Great Ideas destined for wider application: Precision measurement Quantum-classical boundary Many-particle entanglement A uniquely interdisciplinary community that should be nurtured.

Quantum Information Science QIS Quantum Computer