Quantum Channels Optical fibers Quantum memories Any quantum

Quantum Channels: Optical fibers Quantum memories Any quantum operation (without post selection)

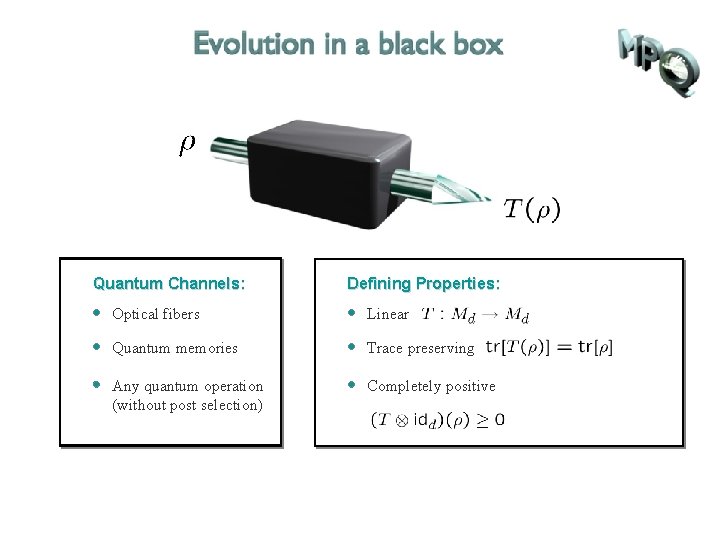
Quantum Channels: Defining Properties: Optical fibers Linear Quantum memories Trace preserving Any quantum operation (without post selection) Completely positive

What does a snapshot tell us about the evolution of a system?

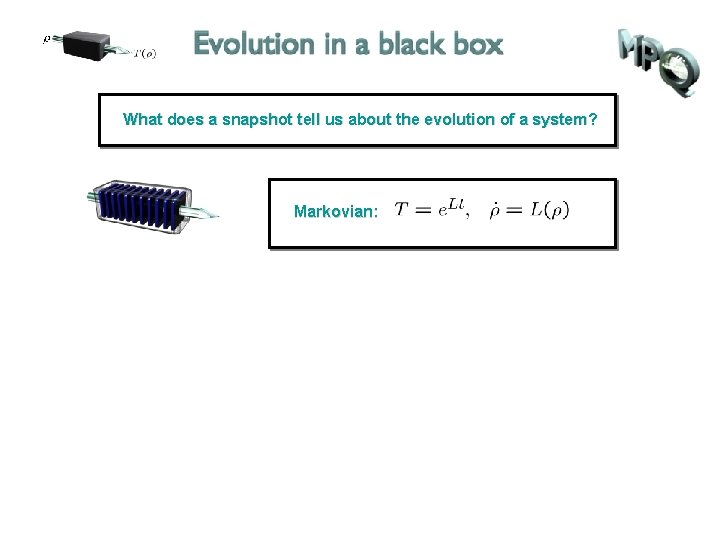
What does a snapshot tell us about the evolution of a system? Markovian:

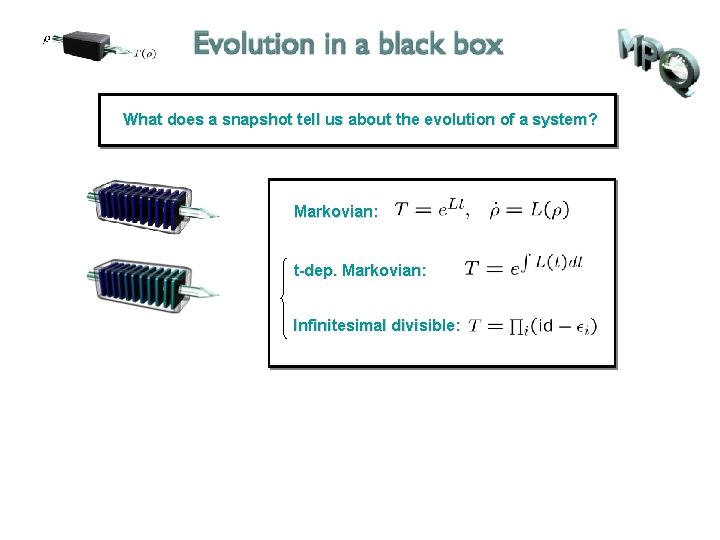
What does a snapshot tell us about the evolution of a system? Markovian: t-dep. Markovian: Infinitesimal divisible:

What does a snapshot tell us about the evolution of a system? Markovian: t-dep. Markovian: Infinitesimal divisible: Divisible:

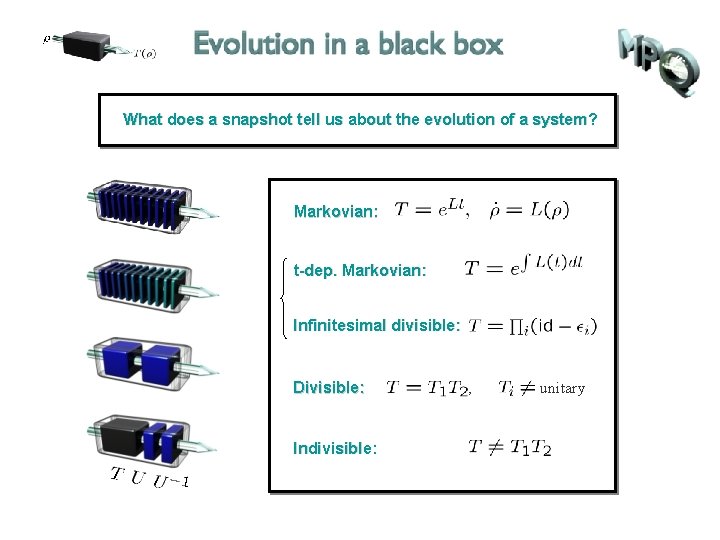
What does a snapshot tell us about the evolution of a system? Markovian: t-dep. Markovian: Infinitesimal divisible: Divisible: Indivisible: , unitary

Ideal channel

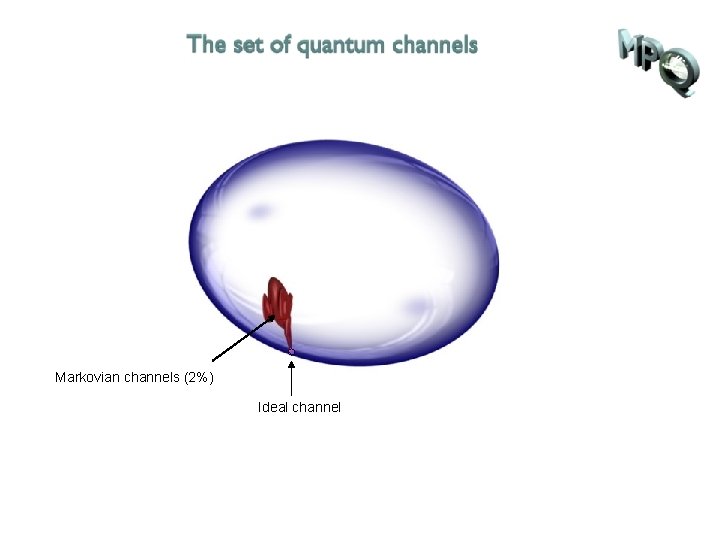
Markovian channels (2%) Ideal channel

t-dep. Markovian = inf. divisible (17%) Markovian channels (2%) Ideal channel

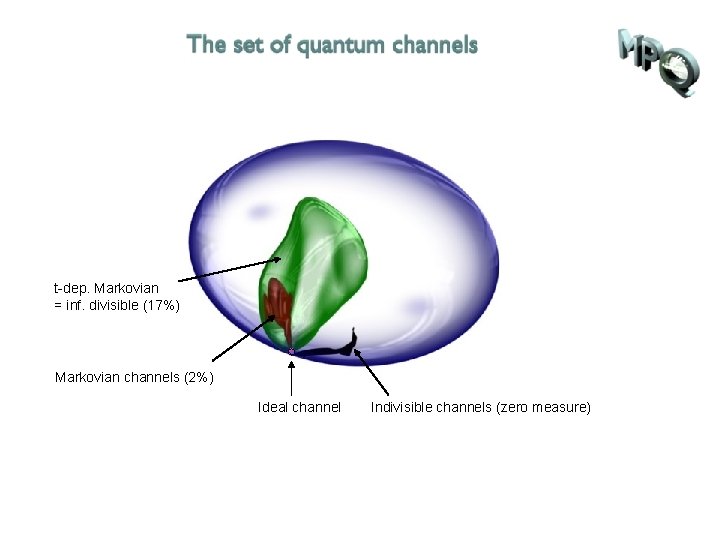
t-dep. Markovian = inf. divisible (17%) Markovian channels (2%) Ideal channel Indivisible channels (zero measure)

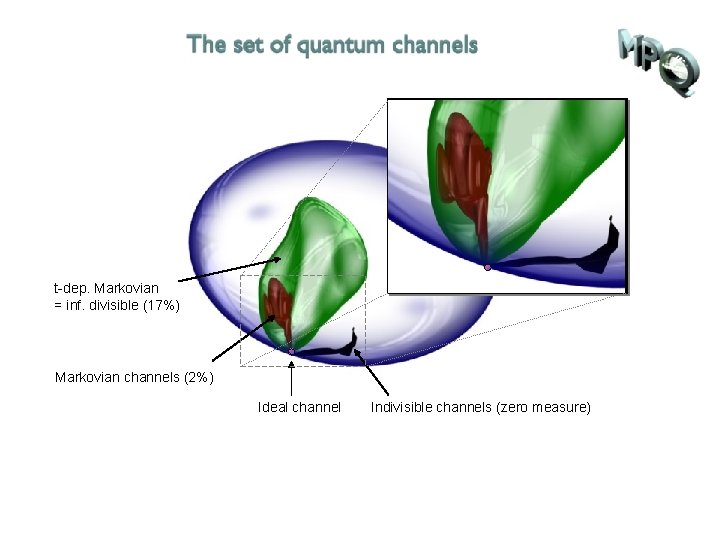
t-dep. Markovian = inf. divisible (17%) Markovian channels (2%) Ideal channel Indivisible channels (zero measure)

Matrix rep. of T “ log T ” Check Lindblad form

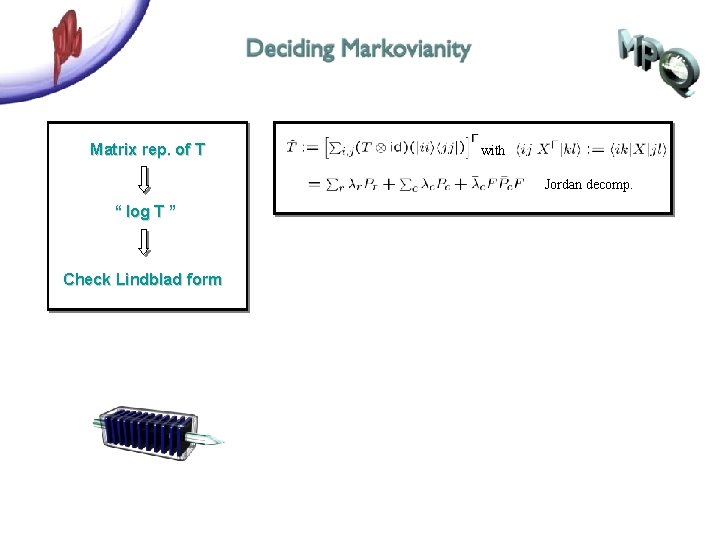
Matrix rep. of T with Jordan decomp. “ log T ” Check Lindblad form

Matrix rep. of T with Jordan decomp. “ log T ” Check Lindblad form

Matrix rep. of T with Jordan decomp. “ log T ” Check Lindblad form

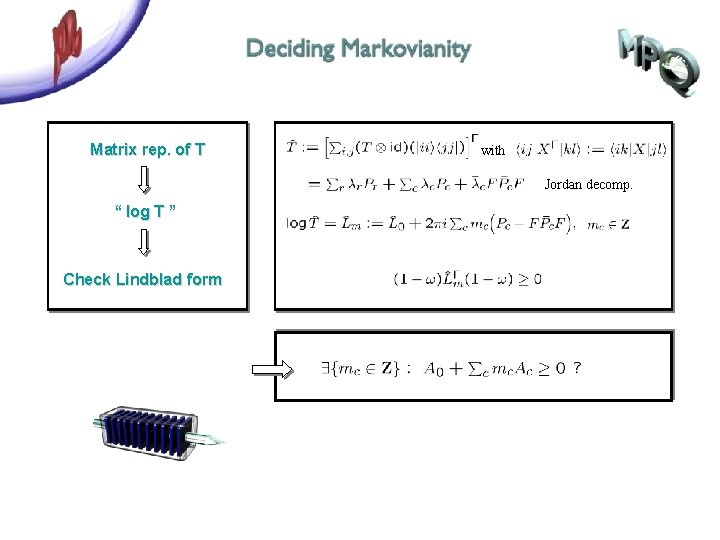
Matrix rep. of T with Jordan decomp. “ log T ” Check Lindblad form

Matrix rep. of T with Jordan decomp. “ log T ” Check Lindblad form semidef. integer program has efficient solution [Khachiyan, Porkolab] becomes NP-hard if d is not fixed

What about ? How to compute? ?

‘Liouvillian’ of master equation non-physical evolution

‘Liouvillian’ of master equation non-physical evolution measure based on rate minimal noise

‘Liouvillian’ of master equation non-physical evolution measure based on rate minimal noise integer s. d. p.

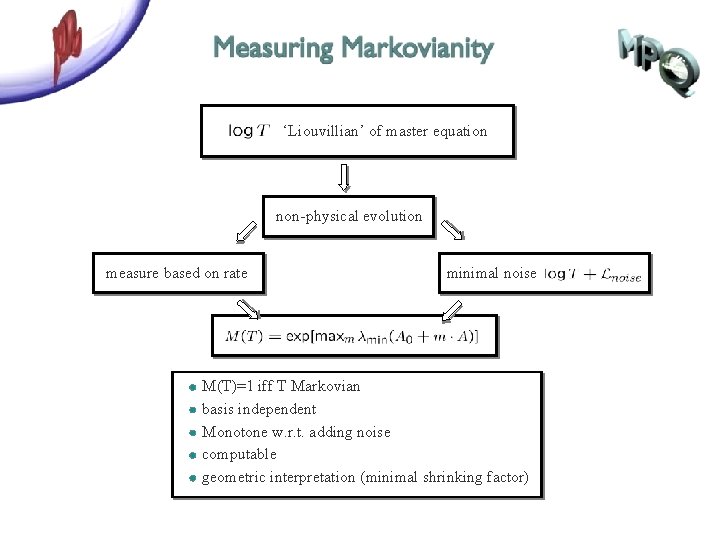
‘Liouvillian’ of master equation non-physical evolution measure based on rate minimal noise M(T)=1 iff T Markovian basis independent Monotone w. r. t. adding noise computable geometric interpretation (minimal shrinking factor)

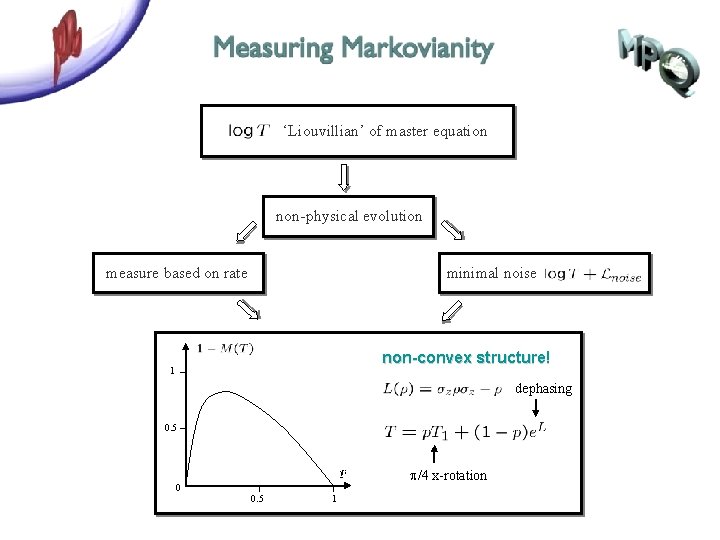
‘Liouvillian’ of master equation non-physical evolution measure based on rate minimal noise non-convex structure! 1 dephasing 0. 5 p/4 x-rotation 0 0. 5 1

Def. : T is infinitesimal divisible if for all e there exist channels s. t.

Def. : T is infinitesimal divisible if for all e there exist channels s. t. Thm. : A channel T is infinitesimal divisible iff

Def. : T is infinitesimal divisible if for all e there exist channels s. t. Thm. : A channel T is infinitesimal divisible iff Thm. : Infinitesimal divisibility is preserved under filtering operations with Kraus rank one

Def. : T is infinitesimal divisible if for all e there exist channels s. t. Thm. : A channel T is infinitesimal divisible iff Thm. : Infinitesimal divisibility is preserved under filtering operations with Kraus rank one Thm. : A qubit channel is infinitesimal divisible iff and with

Def. : T is infinitesimal divisible if for all e there exist channels s. t. Thm. : A channel T is infinitesimal divisible iff Thm. : Infinitesimal divisibility is preserved under filtering operations with Kraus rank one Thm. : A qubit channel is infinitesimal divisible iff and with Thm. : All extremal qubit channels are infinitesimal divisible. non-convex!

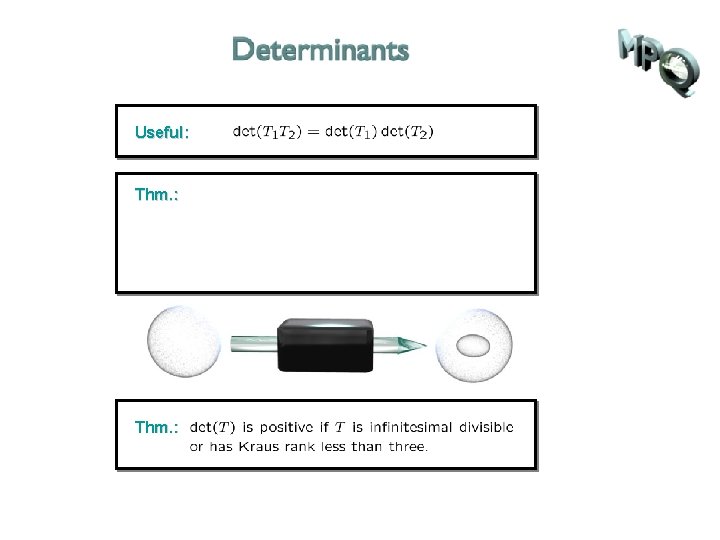
Useful:

Useful: Thm. :

Useful: Thm. :

Useful: Thm. :

Def. :

Def. : Thm. :

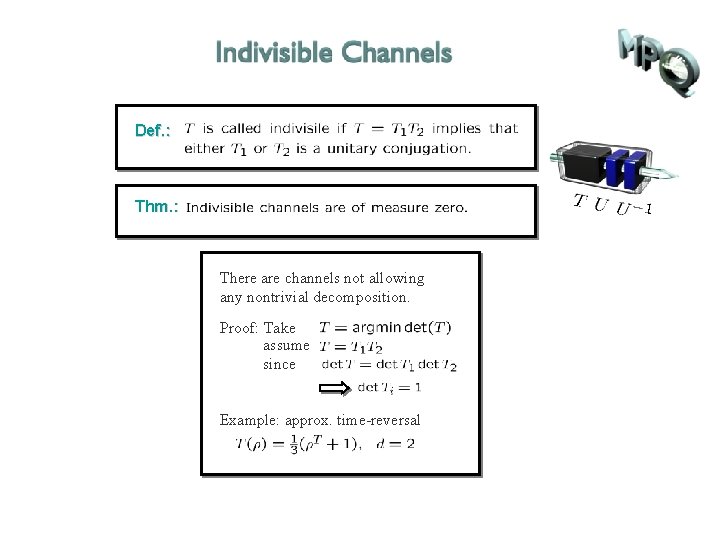
Def. : Thm. : There are channels not allowing any nontrivial decomposition. Proof: Take assume since Example: approx. time-reversal

Def. : Thm. :

• Wolf, Cirac, Comm. Math. Phys. (2008) • Wolf, Eisert, Cubitt, Cirac, ar. Xiv: 0711. 3172 • Cubitt, Eisert, Wolf, Cirac, t. b. p. soon Markovian channels t-dep. Markovian channels Determinants Indivisble channels 1 0. 5 0 0. 5 1