Quantum Computing Intro Overview Whats Quantum Computing All

Quantum Computing Intro. & Overview: What’s Quantum Computing All About?

Classical vs. Quantum Computing • For any digital computer, its set of computational states is some set of mutually distinguishable abstract states. – The specific computational state that is in use at a given time represents the specific digital data currently being processed within the machine. • Classical computing is computing in which: – All of the computational states (at all times) are stable pointer states of the computer hardware. • Quantum computing is computing in which: – The computational state is not always a pointer state.

What is “Quantum Computing? ” • Non-pointer-state computing. • Harnesses these quantum effects on a large, complex scale: – Computational states that are not just pointer states, but also, coherent superpositions of pointer states. • States having non-zero amplitude in many pointer states at the same time! “Quantum parallelism. ” – Entanglement (quantum correlations) • Between the states of different subsystems. – Unitary (thus reversible) evolution through time – Interference (reinforcement and cancellation) • Between convergent trajectories in pointer-state space.

Why Quantum Computing? • It is, apparently, exponentially more timeefficient than any possible classical computing scheme at solving some problems: – Factoring, discrete logarithms, related problems – Simulating quantum physical systems accurately • This application was the original motivation for quantum computing research first suggested by famous physicist Richard Feynman in the early 80’s. • However, this has never been proven yet! – If you want to win a sure-fire Nobel prize… • Find a polynomial-time algorithm for accurately simulating quantum computers on classical ones!

Status of Quantum Computing • Theoretical & experimental progress is being made, but slowly. – There are many areas where much progress is still needed. • Physical implementations of very small (e. g. , 7 -bit) quantum computers have been tested and work as predicted. – However, scaling them up is difficult. • There are no known fundamental theoretical barriers to large-scale quantum computing. – Guess: It will be a real technology in ~20 yrs. or so.

Early History • Quantum computing was largely inspired by reversible computation work from the 1970’s: – Bennett, Fredkin, and Toffoli • Early quantum computation pioneers (1980’s): – Early models not using quantum parallelism to gain performance: • Benioff ‘ 80, ‘ 82 - Quantum serial TM models • Feynman ‘ 86 - Q. models of serial reversible circuits • Margolus ‘ 86, ’ 90 - Q. models of parallel rev. circuits – Performance gains w. quantum parallelism: • Feynman ‘ 82 - Suggested faster quantum sims with QC • Deutsch ‘ 85 - Quantum-parallel Turing machine • Deutsch ‘ 89 - Quantum logic circuits

More Recent History • There was a rapid ramp-up of quantum computing research throughout the 1990’s. • Some developments, 1989 -present – Refining quantum logic circuit models • What is a minimal set of universal gates for QC? – Algorithms: Shor factoring, Grover search, etc. – Developing quantum complexity theory • What is the ultimate power of quantum computation? – Quantum information theory • Communications, Cryptography, etc. • Error correcting codes, fault tolerance, robust QC – Physical implementations • Numerous few-bit implementations demonstrated

Quantum Logic Networks • Invented by Deutsch (1989) – Analogous to classical Boolean logic networks – Generalization of Fredkin-Toffoli reversible logic circuits • System is divided into individual bits, or qubits – 2 orthogonal states of each bit are designated as the computational basis states, “ 0” and “ 1”. • Quantum logic gates: – Local unitary transforms that operate on only a few state bits at a time. • Computation via predetermined seq. of gate applications to selected bits.

Gates without Superposition • All classical input-consuming reversible gates can be represented as unitary transformations! • E. g. , input-consuming NOT gate (inverter) in out 0 1 1 0

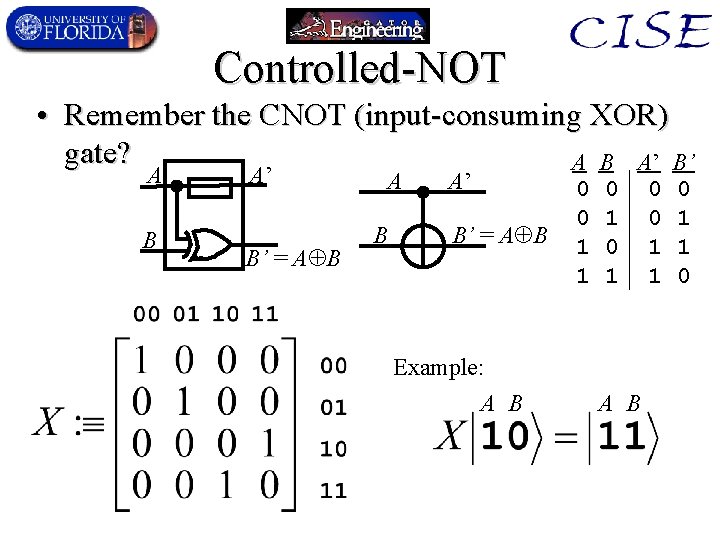
Controlled-NOT • Remember the CNOT (input-consuming XOR) gate? A B A’ B’ = A B Example: A B 0 0 1 1 0 1 A B 0 0 1 1 0

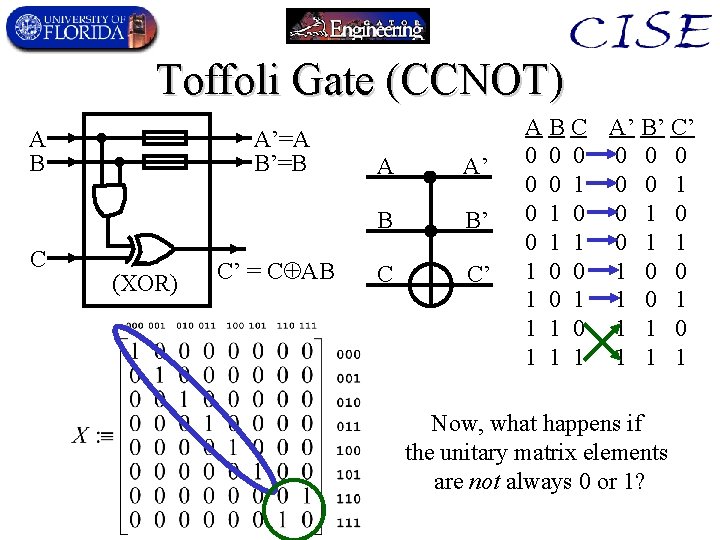
Toffoli Gate (CCNOT) A B C A’=A B’=B (XOR) C’ = C AB A A’ B B’ C C’ A B C A’ B’ C’ 0 0 0 0 1 0 0 1 1 1 0 0 1 0 1 1 1 1 Now, what happens if the unitary matrix elements are not always 0 or 1?

The Square Root of NOT • If you put in either basis state (0 or 1) you get a state that appears random when measured… 0 N 1/2 0 (50%) 1 (50%) • But if you feed the output back into another N 1/2 without measuring it, you get the inverse of the original value! 0 (50%) 0 1 N 1/2 • “How is that possible? ” 0 N 1/2 1 (50%) 0 (50%) 1 (50%) N 1/2 0

NOT 1/2: Unitary implementation Prob. ½

The Hadamard Transform • A randomizing “square root of identity” gate. • Used frequently in quantum logic networks.

Another NOT 1/2 • This one negates the phase of the state if the input state was |0.

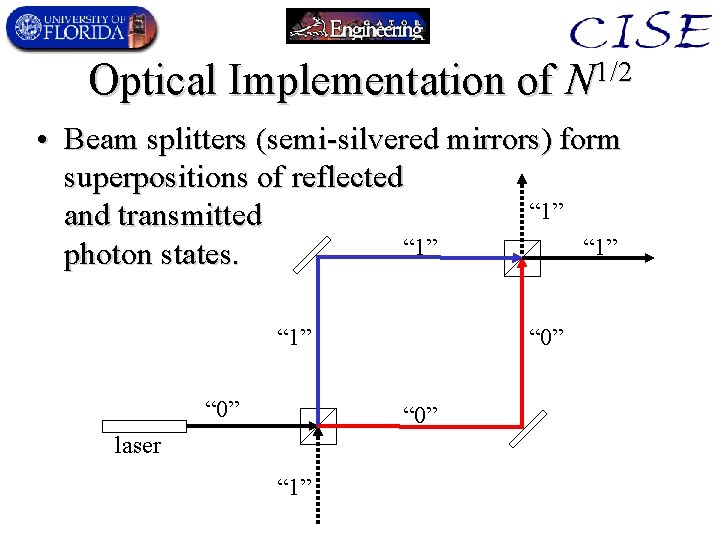
Optical Implementation of N 1/2 • Beam splitters (semi-silvered mirrors) form superpositions of reflected “ 1” and transmitted “ 1” photon states. “ 1” “ 0” laser “ 1”

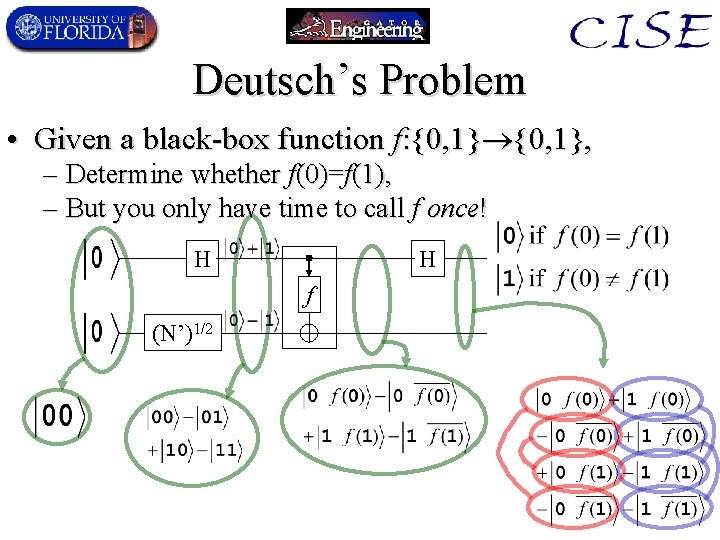
Deutsch’s Problem • Given a black-box function f: {0, 1}, – Determine whether f(0)=f(1), – But you only have time to call f once! H H f (N’)1/2

Extended Deutsch’s Problem • Given black-box f: {0, 1}n {0, 1}, – and a guarantee that f is either constant or balanced (1 on exactly ½ of inputs) – Which is it? – Minimize number of calls to f. • Classical algorithm, worst-case: – Order 2 n time! • What if the first 2 n− 1 cases examined are all 0? – Function could still be either constant or balanced. • Case number 2 n-1+1: if 0, constant; if 1, balanced. • Quantum algorithm is exponentially faster! – (Deutsch & Jozsa, 1992. )

Universal Q-Gates: History • Deutsch ‘ 89: – Universal 3 -bit Toffoli-like gate. • di. Vincenzo ‘ 95: – Adequate set of 2 -bit gates. • Barenco ‘ 95: – Universal 2 -bit gate. • Deutsch et al. ‘ 95 – Almost all 2 -bit gates are universal. • Barenco et al. ‘ 95 – CNOT + set of 1 -bit gates is adequate. • Later development of discrete gate sets. . .

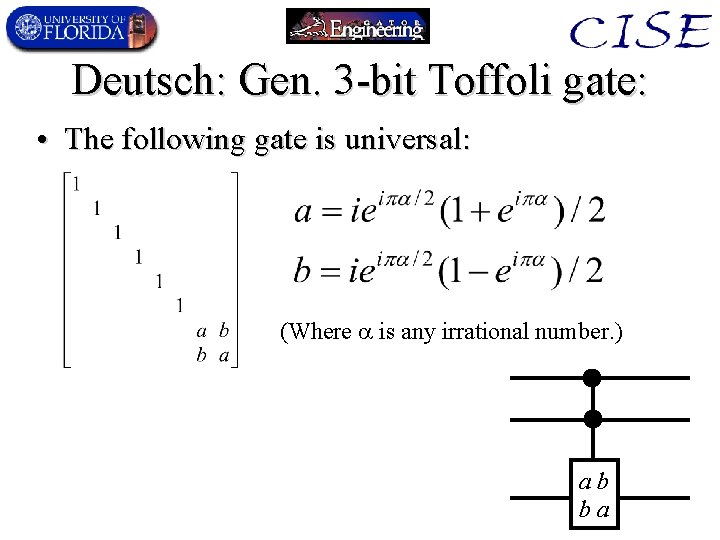
Deutsch: Gen. 3 -bit Toffoli gate: • The following gate is universal: (Where is any irrational number. ) ab ba

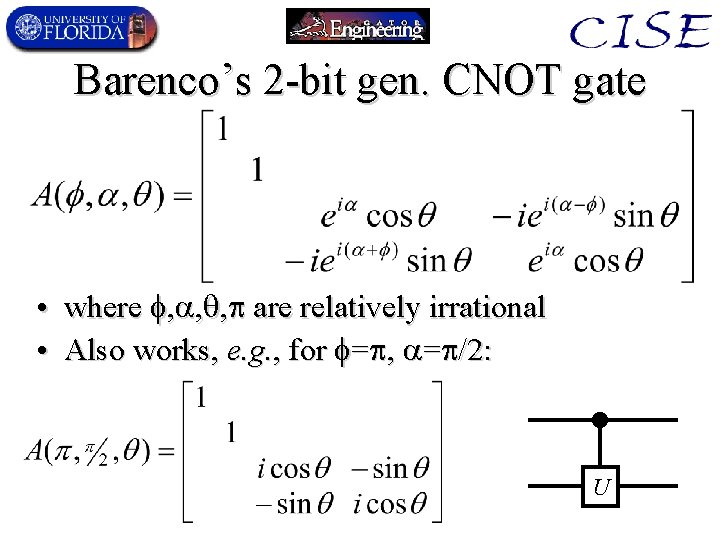
Barenco’s 2 -bit gen. CNOT gate • where , , , are relatively irrational • Also works, e. g. , for = , = /2: U

Barenco et al. ‘ 95 results • Universality of CNOT + 1 -bit gates – 2 -bit Barenco gate already known universal – 4 1 -bit gates + 2 CNOTs suffice to build it • Construction of generalized Toffoli gates – 3 -bit version via five 2 -bit gates – n-bit version via O(n 2) 2 -bit gates – No auxilliary bits needed for the above • All operations done “in place” on input qubits. – n-bit version via O(n) 2 -bit gates, given 1 work bit

Quantum Complexity Theory • Early developments: – Deutch’s problem (from earlier): Slight speedup – Deutsch & Jozsa: Exponential speed-up • Important quantum complexity classes: – EQP: Exact Quantum Polynomial - like P. • Polynomial time, deterministic. – ZQP: Zero-error Quantum Polynomial - like ZPP. • Probabilistic, expected polynomial-time, zero errors. – BQP: Bounded-error Quantum Poly. - like BPP. • Probabilistic, bounded probability of errors. • All results relativized, e. g. , – O: EQPO (NPO co-NPO) Given a certain black-box, quantum computers can solve a certain problem faster than a classical computer can even check the answer!

Quantum Algorithms Part I: Unstructured Search

Unstructured Search Problem • Given a set S of N elements and a black-box function f: S {0, 1}, find an element x S such that f(x)=1, if one exists (or if not, say so). – Any NP problem can be cast as an unstructured search problem. • Not necessarily the optimal approach, however. • Bounds on classical run-time: – (N) expected queries in worst case (0 or 1 sol’ns): • Have to try N/2 elements on average before finding sol’n. • Have to try all N if there is no solution. • If elements are length- bit strings, – Expected #trials is (2 ) - exponential in . Bad!

Quantum Unstructured Search • Minimum time to solve unstructured search problem on a quantum computer is: – (N 1/2) queries = (2 /2) = (21/2) • Still exponential, but with a smaller base. • The minimum # of queries can be achieved using Grover’s algorithm.

Grover’s algorithm: • 1. Start w. amplitude evenly distributed among the N elements, (xi)=1/ N x 1 solution xs x. N • 2. In each state xi, compute f(xi): • 3. Apply conditional phase shift of if f(xi)=1 (Negate sign of solution state. ) Uncompute f. f=0 f=1 x 1 solution xs x. N

Grover’s algorithm, cont. • 4. Invert all amplitudes with respect to the average amplitude: x 1 solution xs x. N

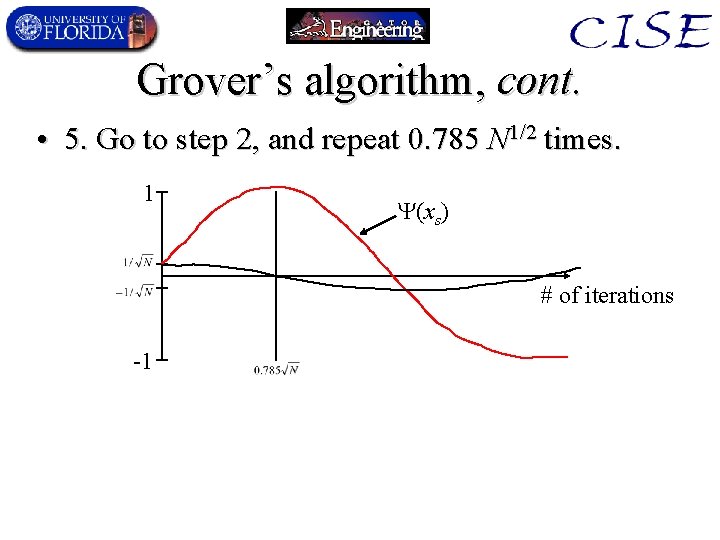
Grover’s algorithm, cont. • 5. Go to step 2, and repeat 0. 785 N 1/2 times. 1 (xs) # of iterations -1

Shor’s Factoring Algorithm • Solves the >2000 -year-old problem: – Given a large number N, quickly find the prime factorization of N. (At least as old as Euclid!) • No polynomial-time (as a function of n=lg N) classical algorithm for this problem is known. – The best known (as of 1993) was a number field sieve algorithm taking time O(exp(n 1/3 log(n 2/3))) – However, there is also no proof that an (undiscovered) fast classical algorithm does not exist. • Shor’s quantum algorithm takes time O(n 2) – No worse than multiplication of n-bit numbers!

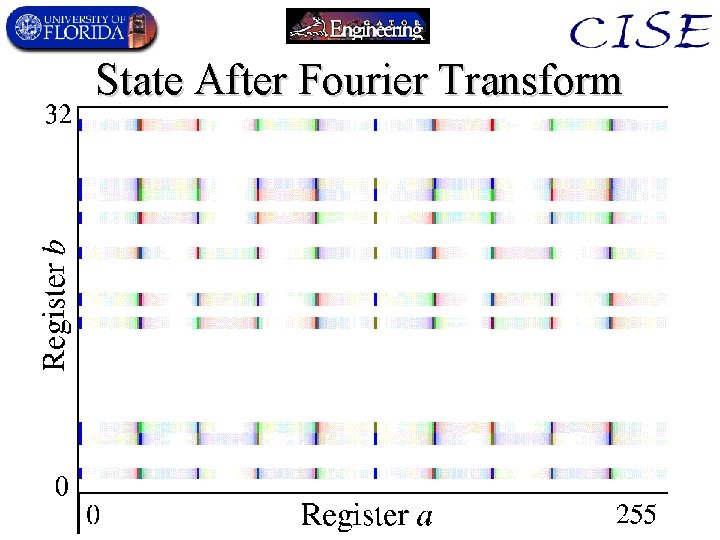
Elements of Shor’s Algorithm • Uses a standard reduction of factoring to another number-theory problem called the discrete logarithm problem. • The discrete logarithm problem corresponds to finding the period of a certain periodic function defined over the integers. • A general way to find the period of a function is to perform a Fourier transform on the function. – Shor showed how to generalize an earlier algorithm by Simon, to provide a Quantum Fourier Transform that is exponentially faster than classical ones.

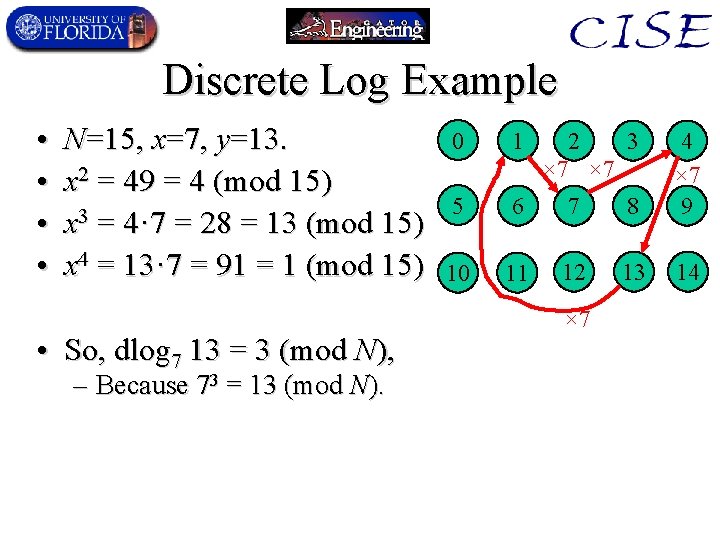
Powers of numbers mod N • Given natural numbers (non-negative integers) N 1, x<N, and x, consider the sequence: x 0 mod N, x 1 mod N, x 2 mod N, … = 1, x, x 2 mod N, … • If x and N are relatively prime, this sequence is guaranteed not to repeat until it gets back to 1. • Discrete logarithm of y, base x, mod N: – The smallest natural number exponent k (if any) such that xk = y (mod N). – I. e. , the integer logarithm of y, base x, in modulo-N arithmetic. Example: dlog 7 13 (mod N) = ?

Discrete Log Example • • N=15, x=7, y=13. x 2 = 49 = 4 (mod 15) x 3 = 4· 7 = 28 = 13 (mod 15) x 4 = 13· 7 = 91 = 1 (mod 15) • So, dlog 7 13 = 3 (mod N), – Because 73 = 13 (mod N). 0 1 5 6 7 8 4 × 7 9 10 11 12 13 14 2 3 × 7 × 7

The order of x mod N • Problem: Given N>0, and an x<N that is relatively prime to N, what is the smallest value of k>0 such that xk = 1 (mod N)? – This is called the order of x (mod N). • From our previous example, the order of 7 mod N is…? 0 1 5 6 7 8 4 × 7 9 10 11 12 13 14 2 3 × 7 × 7

Order-finding permits Factoring • A standard reduction of factoring N to finding orders mod N: – 1. Pick a random number x < N. – 2. If gcd(x, N) 1, return it (it’s a factor). – 3. Compute the order of x (mod N). • Let r : = min k>0: xk mod N = 1 – 4. If gcd(xr/2 1, N) 1, return it (it’s a factor). – 5. Repeat as needed. • The expected number of repetitions of the loop needed to find a factor with probability > 0. 5 is known to be only polynomial in the length of N.

Factoring Example • • • For N=15, x=7… 0 1 2 3 × 7 Order of x is r=4. 5 6 7 8 r/2 = 2. x 2 = 5. 13 10 11 12 In this case (we are lucky), × 7 2 2 both x +1 and x 1 are factors (3 and 5). • Now, how do we compute orders efficiently? 4 × 7 9 14

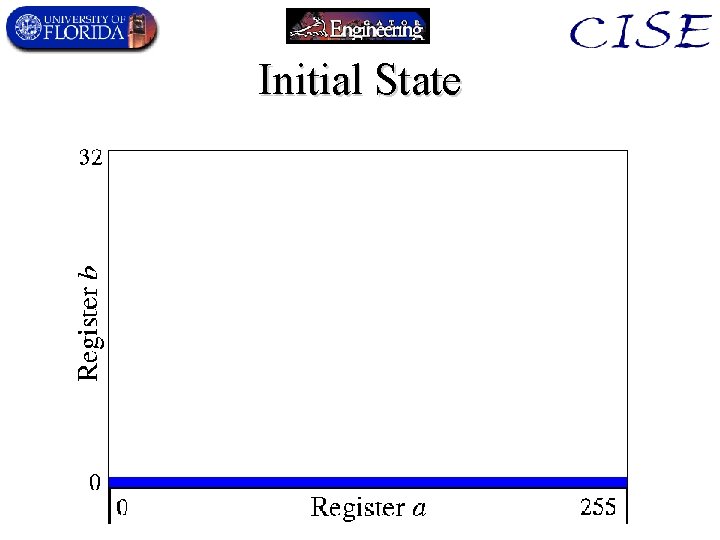
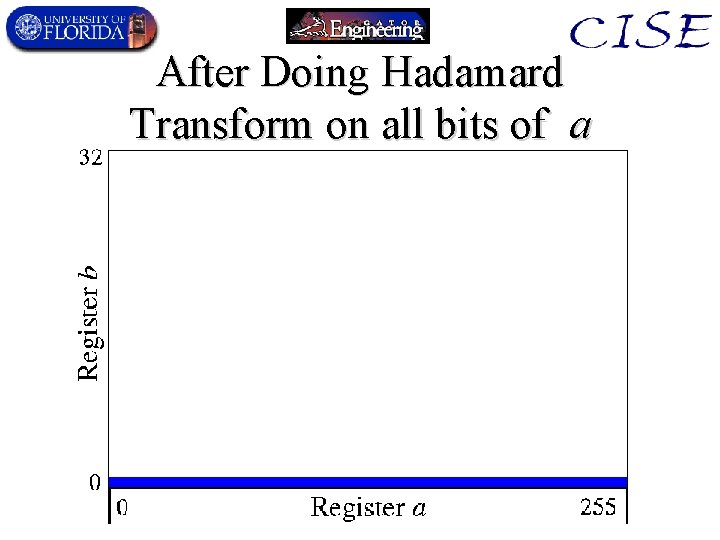
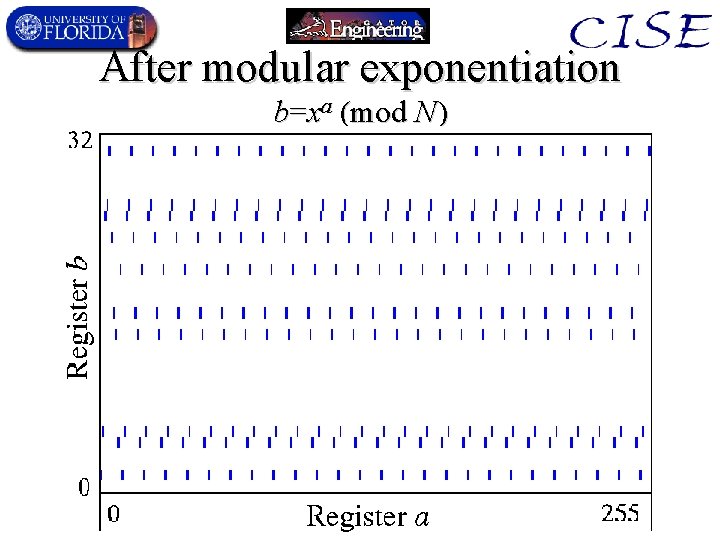
Quantum Order-Finding • Uses 2 quantum registers (a, b) – 0 a < q, is the k (exponent) used in order-finding. – 0 b < n, is the y (xk mod n) value – q is the smallest power of 2 greater than N 2. • Algorithm: – 1. Initial quantum state is |0, 0 , i. e. , (a=0, b=0). – 2. Go to superposition of all possible values of a:

Initial State

After Doing Hadamard Transform on all bits of a

After modular exponentiation b=xa (mod N)

State After Fourier Transform

Quantum Algorithms III Wrap-up: Classical vs. Quantum Parallelism Quantum Physics Simulations

Classical Unstructured Search • The classical serial algorithm takes (N) time. • But: Suppose we search in parallel! – Have M<N processors running in parallel. – Each searches a different subset of N/M elements of the search space. – If processors are ballistic reversible: • Can cluster them in a dense mesh of diameter (M 1/3). • Time accounting: M 1/3 M – Computation time: (N/M) – Communication time: (M 1/3) (at lightspeed) – Total: T N/M + M 1/3 is minimized when M N 3/4 N 1/4 Faster than Grover’s algorithm!

Classical+Quantum Parallelism • Similar setup to classical parallelism: – M processors, searching N/M items each. – Except, each processor uses Grover’s algorithm. • Time accounting: – Computation: – Communication: – Total: T (N/M)1/2 T M 1/3 (as before) T (N/M)1/2 + M 1/3 • Total is minimized when M N 3/5 – Minimized total is T N 1/5. • I. e. , quantum unstructured search is really only N 1/4/N 1/5 = N 1/20 × faster than classical!

Simulating Quantum Physics • For n particles, takes exponential time using the best known classical methods. – Feynman suggested: use quantum computing • Takes only polynomial time on a QC. • History of some fast QC physics algorithms: – Schrödinger equation (Boghosian, Yepez) – Many-body Fermi systems (Abrams & Lloyd) – Eigenvalue/eigenvector computations (ditto) – Quantum lattice gases, Ising models, etc. – Totally general quantum physics simulations (Field theories, etc. ) - Lloyd 1996

Simulating Quantum Computers on classical ones

Efficient QC Simulations • Task: Simulate an n-qubit quantum computer. • Maximally stupid approach: – Store a 2 n-element vector – Multiply it by a full 2 n× 2 n matrix for each gate op • Some obvious optimizations: – Never store whole matrix (compute dynamically) – Store only nonzero elements of state vector • Especially helpful when qubits are highly correlated – Do only constant work per nonzero vector element • Scatter amplitude from each state to 1 or 2 successors – Drop small-probability-mass sets of states • Linearity of QM implies no chaotic growth of errors

Linear-space quantum simulation • A popular myth: – “Simulating an n-qubit (or n-particle) quantum system takes e (n) space (as well as time). ” • The usual justification: – It takes e (n) numbers even to represent a single (n)-dimensional state vector, in general. • The hole in that argument: – Can simulate the statistical behavior of a quantum system w/o ever storing a state vector! • Result BQP PSPACE known since BV’ 93. . . – But practical poly-space sims are rarely described

The Basic Idea • Inspiration: – Feynman’s path integral formulation of QED. – Gives the amplitude of a given final configuration by accumulating amplitude over all paths from initial to final configurations. – Each path consists of only a single (n)-coordinate configuration at each time, not a full wavefunction over the configuration space. – Can enumerate all paths, while only ever representing one path at a time.

Simulating Quantum Computations • Given: – Any n-qubit quantum computation, expressed as a sequence of 1 -qubit gates and CNOT gates. U 2 U 1 U 3 U 4 – An initial state s 0 which is just a basis state in the classical bitwise basis, e. g. 00000. • Goal: – Generate a final basis state stochastically with the same probability distribution as the quantum computer would do.

Matrix Representation • Consider each gate as rank-2 n unitary matrix: – Each CNOT application is a 0 -1 (permutation) matrix - a classical reversible bit-operation. – With appropriate row ordering, each Ui gate application is block-diagonal, w. each 2× 2 block equal to Ui. – We need never represent these full matrices! – The 1 or 2 nonzero entries in a given row can be located & computed immediately given the row id (bit string) and Ui.

The Linear-Space Algorithm • • • Generate a random “coin” c [0, 1]. Initialize probability accumulator: p 0. For each final n-bit string y at time t, – Compute its amplitude (y) as follows: • Generate its possible 1 or 2 predecessor strings x 1 (and maybe x 2) given the gate-op preceding t. • For each predecessor, compute its amplitude at time t 1 recursively using this same algorithm, – unless t=0, in which case =1 if x =s 0, 0 otherwise. • Add predecessor amplitudes, weighted by entries. – Maybe output y, using roulette wheel algorithm: • Accumlate Pr[y] into total: p p +|| (y)||2 • Output y and halt if p>c.

A Further Optimization • Don’t even have to enumerate all final states! – Instead: Stochasically follow a trajectory. • Basic idea: – Keep track of 1 “current” state & its amplitude 0. – For CNOTs: Deterministically transform state. – For Us: Calculate amplitude 1 of “neighbor” state w. path-integral Calculate amplitudes 0 and 1 after qubit op Choose 1 successor as new current state, using | |2 distrib. u 00 Current state ’ 0 0 Possible u 10 u 01 successors 1 “Neighbor” state u 11 ’ 1 • • •

Complexity Comparison • To simulate t gate ops (c CNOTs + u 1 -bit unitary ops) of an n-qubit quantum computer: Space Time Traditional method: 2 n t· 2 n Path-integral method: t ·n n· 2 t – (Actually, only the u unitary ops, not all t ops or all n qubits, contribute to any of the exponents here. ) • Upshot: – Lower space usage can allow larger systems to be simulated, for short periods. – Run time is competitive for case when t < n

Quantum Information & Communication Decoherence Quantum Error Correction Quantum Cryptography

Decoherence • The effect that makes macroscopic quantum systems appear to behave “classically. ” – Theory was developed in many papers by Zurek. • Occurs due to inevitable interactions between a given quantum system & an unknown (highentropy) environment. – Interaction increases (von Neumann-) entropy of the reduced density matrix of the quantum system. • Quantum state gradually “collapses” or “decays” to a classical statistical mixture of the pointer states (measurement eigenstates).

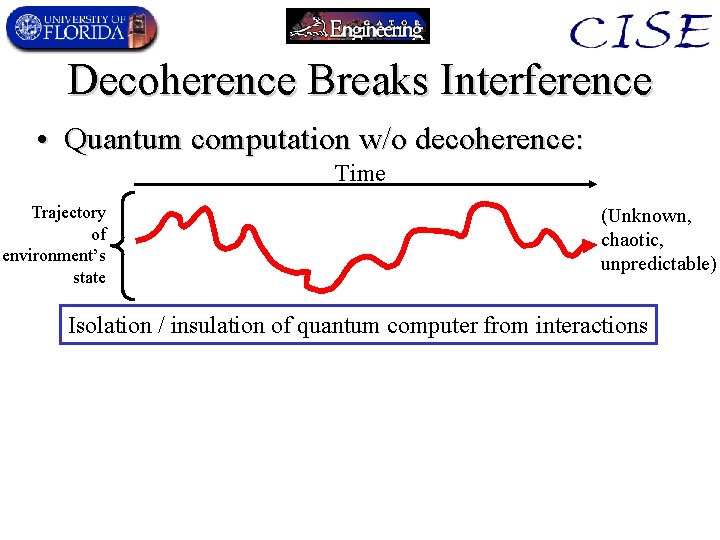
Decoherence Breaks Interference • Quantum computation w/o decoherence: Time Trajectory of environment’s state (Unknown, chaotic, unpredictable) Isolation / insulation of quantum computer from interactions

Quantum Information & Communication cont. Quantum Cryptography

The Key Distribution Problem • How can parties A and B use a physically insecure long-distance communications channel to nevertheless securely exchange keys that they can use to enable future secure, encrypted communication between them? • Present-day solution: Public-Key Cryptography – see next slide

Public-Key Cryptography • A and B each prepare a pair of a public key and a corresponding private key. – Infeasible to compute private key from public one. • They openly publish their public keys. • Anyone can now use the public key to encrypt messages to A or B. – But only the one w. the matching private key can decrypt the message. • Security of technique depends on existence of one-way (a. k. a. trapdoor) functions. – functions believed (but unproven) to be such.

PK Crypto vs. Q-Computing • A serious weakness in most present-day PK cryptosystems (such as RSA): – They depend for their security on the “one-wayness” of certain functions that is due to the hardness of the factoring and discrete logarithm problems. – But, Shor’s algorithm gives a fast way to solve these problems if we just had a quantum computer! • Large QCs may be implemented within next 10 -20 years. • Therefore, data encrypted today with these cryptosystems cannot be considered secure over multi-decade time-frames! – But, other PK systems w/o this weakness may exist.

Q-Cryptography to the Rescue! • Features: – Provides for secure key exchange over physically unprotected channels w. a guarantee of detection of any eavesdropping of the key. • Doesn’t protect against denial-of-service attacks. – Physically impossible to compromise security (except @ endpoints) barring overthrow of physics! • Provably secure under known laws – Experimentally verified to work perfectly over >48 km distances (so far) (Hughes ‘ 99) via fiber-optic networks.

The One-Time Pad • The only known provably secure cryptosystem. • Based on a key of the same length as the data to be encrypted. – A given key can only be used once. • The key is simply a random string of bits. • The plaintext is bitwise-XORed with the key to produce ciphertext. • Provably secure because any plaintext is equally likely to produce the same ciphertext. • The only problem: How to send the key?

Outline of QC Protocol (BB 84) • A chooses a random bit-string – A key for later use as a one-time pad. • A sends each bit as a qubits with a randomlychosen basis (out of 2 different bases). • B measures each bit in a randomly-chosen basis (out of the same 2 bases). • A & B publicly determine which bits they chose the same bases for. • They publicly spot-check a random subset of the bits for errors, and use remaining bits.

Typical Implementation Method • Any “flying qubit” will do. Arbitrary choice of basis: – Most common method uses polarized photons. (Bennett & Brassard ‘ 84) “ 1” “ 0” Diffraction grating w. vertical slits “ 1” + /4 “ 0” Diffraction grating w. diagonal slits

QC Crypto Protocol - details • 1. A chooses a random bit-string: BB 84 – 1 0 1 1 0 0 1 1 1 1 0 0 • 2. A chooses a random string of polarization bases, out of , : • 3. A encodes bits as photons polarized in the chosen basis:

QC Crypto Protocol - details • 2. A chooses a random string of polarization bases, out of , : • 3. A encodes bits as photons polarized in the chosen basis: • 4. Photons are sent to B over open channel, w. possible noise and/or eavesdropping:

QC Crypto Protocol - details • 3. A encodes bits as photons polarized in the chosen basis: • 4. Photons are sent to B over open channel, w. possible noise and/or eavesdropping: • 5. B chooses random string of polarization bases to measure with:

QC Crypto Protocol - details • 4. Photons are sent to B over open channel, w. possible noise and/or eavesdropping: • 5. B chooses random string of polarization bases to measure with: • 6. B measures photon state w. r. t. his bases: 1 0 1 0 0 1 1 0 0 0 1 1 1 0

QC Crypto Protocol - details • 5. B chooses random string of polarization bases to measure with: • 6. B measures photon state w. r. t. his bases: 1 0 1 0 0 1 1 0 0 0 1 1 1 0 • 7. A & B publicly compare basis choices, determined which matched:

QC Crypto Protocol - details • 6. B measures photon state w. r. t. his bases: 1 0 1 0 0 1 1 0 0 0 1 1 1 0 • 7. A & B publicly compare basis choices, determined which matched: • 8. Now, they expect their bits w. matching bases to match (others are discarded): A 1 0 1 1 0 0 1 1 1 1 0 0 B 1 0 1 0 0 1 1 0 0 0 1 1 1 0

QC Crypto Protocol - details • 7. A & B publicly compare basis choices, determined which matched: • 8. Now, they expect their bits w. matching bases to match (others are discarded): A 1 0 1 1 0 0 1 1 1 1 0 0 B 1 0 1 0 0 1 1 0 0 0 1 1 1 0 • 9. They compare some of these bits publicly to determine level of errors and/or eavesdropping: • Or, compare parities of random subsets (avoids waste)

QC Crypto Protocol - details • 8. Now, they expect their bits w. matching bases to match (others are discarded): A 1 0 1 1 0 0 1 1 1 1 0 0 B 1 0 1 0 0 1 1 0 0 0 1 1 1 0 • 9. They compare some of these bits publicly to determine level of errors and/or eavesdropping: • Or, compare parities of random subsets (avoids waste) • 10. Use remaining bits in the clean part of data as the key for 1 -time pad: 1 1 0 Or, hash these bits down to a smaller but more secure bit-string (“privacy amplification”)

Quantum Crypto Scalability • Optic fiber lengths ~60 -100 km not feasible due to attenuation. • Free-space (air/vacuum) transmission being explored. – Useful in networks of orbiting satellites? • Given quantum computers, can build quantum repeaters that apply quantum error correction to clean up noisy signals? – Can then maintain secure quantum cryptography throughout large networks (quantum internet? ) – Research topic currently under investigation. . .

Physical Implementations of Quantum Computing

Implementation Requirements • 1. Scalable physical system w. wellcharacterized qubits. Di. Vincenzo ‘ 00 – Internal/external coupling parameters accurately known. • 2. Initializability to a standardized state. – Necessary for error correction. – Speed of cooling/measurement is important. • 3. Decoherence time >> gate operation time – >104 -105 x for robust, fault-tolerant operation – Only computational degrees of freedom need long decoherence times.

Implementation Reqs. , cont. • 4. A Universal set of quantum gate operations – Controllable interactions generating desired Us. – 1 - and 2 -body interactions suffice – Parallel ops are necessary for fault-tolerance. • 5. Bit-specific, amplifiable measurements – High quantum efficiency, or else redundancy. – Shouldn’t disturb the rest of the computer. Also for quantum crypto, comm. , & distributed computing: • 6. Faithful transmission of “flying qubits. ” • 7. Interconversion btw. stationary & flying.