Quantum Computing MAS 725 Hartmut Klauck NTU 5

Quantum Computing MAS 725 Hartmut Klauck NTU 5. 3. 2012

More about measurements(I) Some linear algebra: ¢ Vector space V (dimension d) ¢ Subspaces: U µ V and U is also a vector space (dim e < d) ¢ There is an orthonormal basis: v 1, . . . , ve, . . . , vd, span(v 1, . . . , ve)=U ¢ Projection onto U: ¢ PU = i=1. . . e | v iih vi | ¢ Example: Projector P=|v 1 ih v 1| P |v 1 i = |v 1 ih v 1| v 1 i = |v 1 i P ( |v 1 i+ |v 2 i)= |v 1 i + |v 1 ih v 1| v 2 i = |v 1 i ¢

Measurements (II) ¢ ¢ A? B iff v? w for all v 2 A, w 2 B A © B=V iff A? B and for all v 2 V: v = u + w, u 2 A, w 2 B, kuk, kvk = 1, | |2 + | |2=kvk 2

Measurements (III) ¢ ¢ ¢ ¢ Hilbert spaces V, dim k Observable: System l · k of subspaces S 0, . . . , Sl-1, pairwise orthogonal S 0© ©Sl-1 = V Probability of measuring i is k Proj(Si) | i k 2 The state | i collapses to Proj(Si) | i / k. Proj(Si) | ik (renormalized) Observables correspond to a measurement device We only consider projections measurements

Measurements (IV) ¢ ¢ A matrix A is Hermitian, if A=Ay Hermitian matrices have only real eigenvalues and are diagonalizable: l Uy A U is diagonal for some unitary U The eigenspaces of A decompose Cn l Cn=©Vi Let ¸(i) denote an eigenvalue of A, and Pi the projection onto its eigenspace l Then A= i ¸(i) Pi

Measurements (V) ¢ A Hermitian matrix is a concise representation of an observable l Eigenvalues correspond to measurement outcomes l Eigenspaces decompose Cn

Measurements: example ¢ ¢ ¢ Two qubits, living in C 4 Observable: S 0=span(|00 i, |01 i) S 1=span(|10 i, |11 i) S 0 ? S 1 This observable corresponds to measuring the first qubit: S 0 indicates that it is 0, S 1 indicates 1

Measuring an EPR-Pair ¢ ¢ ¢ The state is 1/21/2 ¢ (|00 i+|11 i) We measure the first qubit Result: If we measure 0, then the state collapses to |00 i If we measure 1 we get |11 i Each happens with probability ½ Qubit 2 collapses right after measuring qubit 1 The qubits act like a shared public coin toss. This is even true if the qubits are spatially separated

Summary ¢ ¢ ¢ ¢ Hilbert space: register holding a quantum state Vectors: states Unitary transformation: evolution of states (computation) Observables: for measuring the computation‘s output The probability distribution on results: output of the computation Projected and normalized vector: the remaining quantum state Measurement is the only way to extract information from a quantum state

More about qubits ¢ ¢ ¢ No-Cloning Theorem Bell states Quantum Teleportation

No Cloning ¢ ¢ ¢ Suppose we are given a quantum state | i Can we make a copy? Copying classical information is trivial (ask the music industry about that…) I. e. , there is a unitary transformation Un: Un|xi|0 i = |xi|xi for all x 2{0, 1}n But then by linearity U 1 1/2. 5(|0 i+|1 i) |0 i= 1/21/2 (|00 i+|11 i) 1/21/2(|0 i+|1 i) times 1/2. 5(|0 i+|1 i)

No Cloning Theorem ¢ Theorem: There is no unitary U, such that for all quantum states | i on n qubits: U | i |0 mi = | i | ( )i ¢ for some m und | ( )i (which is garbage) I. e. there is no universal way to copy unknown quantum states without error! ¢ [Dieks, Wootters/Zurek 82]

Proof: No Cloning ¢ ¢ ¢ Let a linear U be given (this also fixes m). Then U |0 ni |0 mi =|0 ni | 0 i U |1 ni |0 mi =|1 ni | 1 i ¢ Then also (due to linearity) U 1/21/2 ( |0 ni+|1 ni ) |0 mi = 1/21/2 ( U |0 ni|0 mi + U |1 ni|0 mi ) = 1/21/2 ( |02 ni | 0 i + |12 ni | 1 i ) ¢ But we wanted (for some | 2 i) 1/2 (|0 ni+|1 ni) | 2 i

Proof: No Cloning (II) ¢ We have 1/21/2 ( |02 ni | 0 i + |12 ni | 1 i ) We want 1/2 (|0 ni+|1 ni) | 2 i ¢ Claim: This is not the same! ¢ Proof of the claim: we compute the inner product. Same state ) inner product = 1 h | i = h | i ¢ h | i h + | i=h | i + h | i ¢ ¢ ¢

Proof No Cloning (III) ¢ ¢ We get 1/21/2 ( |02 ni | 0 i + |12 ni | 1 i ) We expect 1/2 (|0 ni+|1 ni) | 2 i Inner product: 1/23/2 ¢ ( ( h 0 n|0 ni+h 0 n|1 ni ) ¢ h 0| 2 i ) +( h 1 n|0 ni+h 1 n|1 ni) ¢ h 1| 2 i ) ) = 1/23/2 ¢ (1 ¢ a 0, 2 + 1 ¢ a 1, 2). Then |1/23/2 ¢ ( a 0, 2+a 1, 2)| · 2/23/2 < 1

No Cloning ¢ ¢ No unitary can map both a state and another state that are not orthogonal in a way that wakes a copy It is possible to clone quantum states with small success probability

Bell States ¢ Consider the following basis (John Bell) ¢ This is orthonormal in C 4

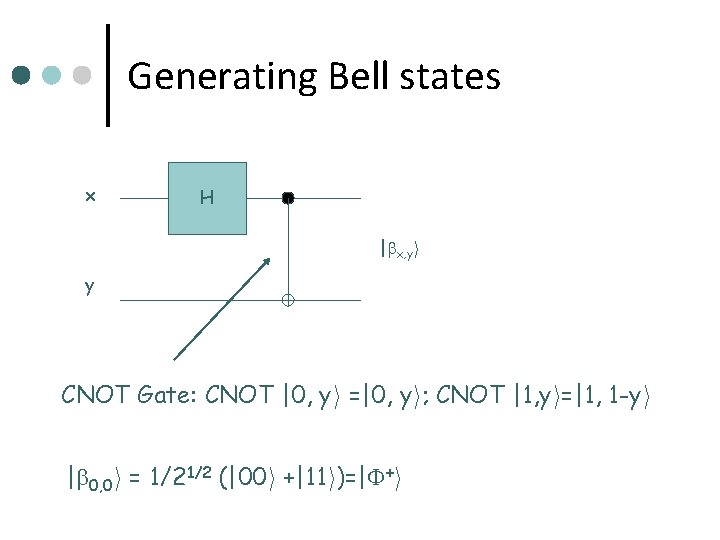
Generating Bell states x H | x, yi y CNOT Gate: CNOT |0, yi =|0, yi; CNOT |1, yi=|1, 1 -yi | 0, 0 i = 1/21/2 (|00 i +|11 i)=| +i

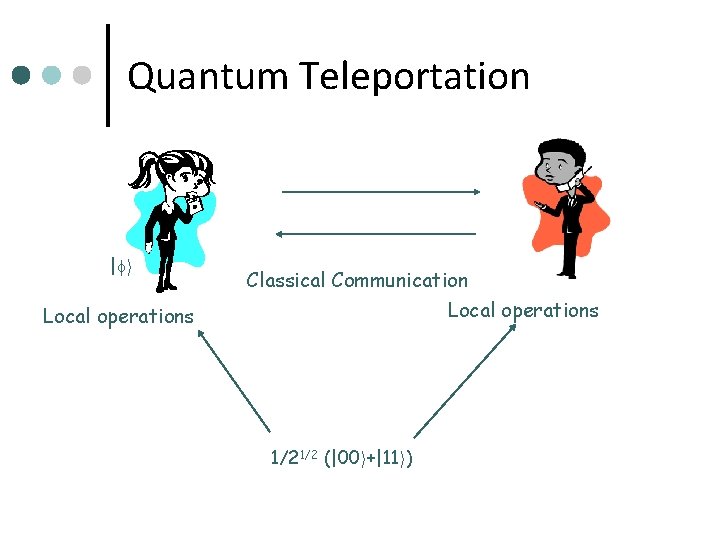
Quantum Teleportation ¢ ¢ ¢ We are given a quantum state | i Can we reproduce that state in another location? We cannot just send them over…. And we cannot copy them Classical communication is possible This problem seems hard since a single qubit 0 |0 i+ 1 |1 i might contain a lot of information due to possibly irrational amplitudes

Quantum Teleportation | i Local operations Classical Communication Local operations 1/21/2 (|00 i+|11 i)

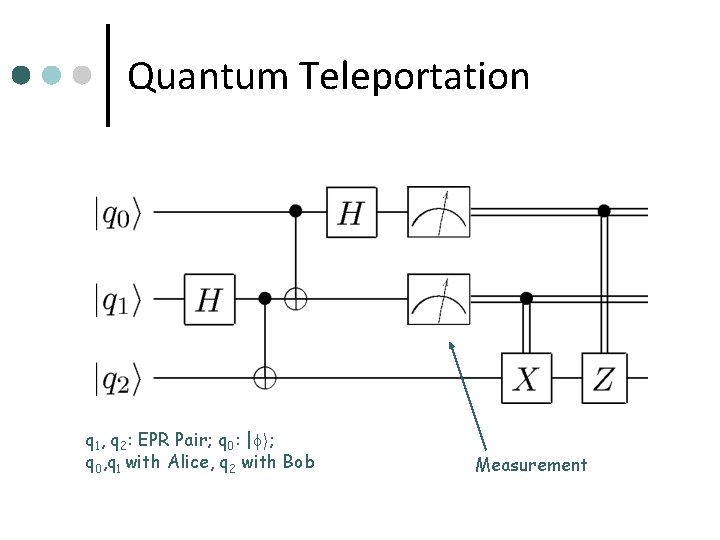
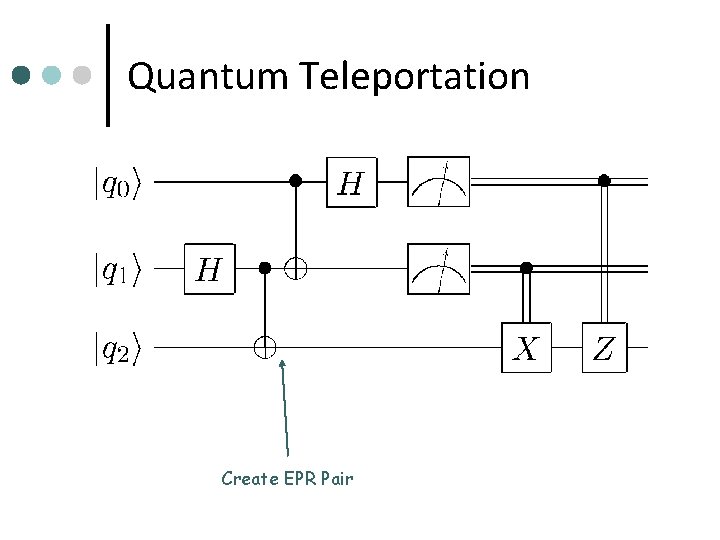
Quantum Teleportation ¢ ¢ ¢ ¢ [Bennett et al. 93] Alice and Bob share an EPR pair (Alice has the first qubit, Bob the other) Alice has | i (1 qubit quantum state) Alice applies CNOT to her qubit q 0 with | i (control) and her EPR qubit q 1 Alice applies H to q 0 and measures q 0 and q 1 Alice sends the result of the measurement (2 bits) Bob applies a unitary transformation depending on the message to his EPR qubit q 2

Quantum Teleportation q 1, q 2: EPR Pair; q 0: | i; q 0, q 1 with Alice, q 2 with Bob Measurement

Pauli Transformations ¢ X: (NOT, Bit Flip) ¢ Z: (Phase Flip) ¢ Y:

Quantum Teleportation Create EPR Pair

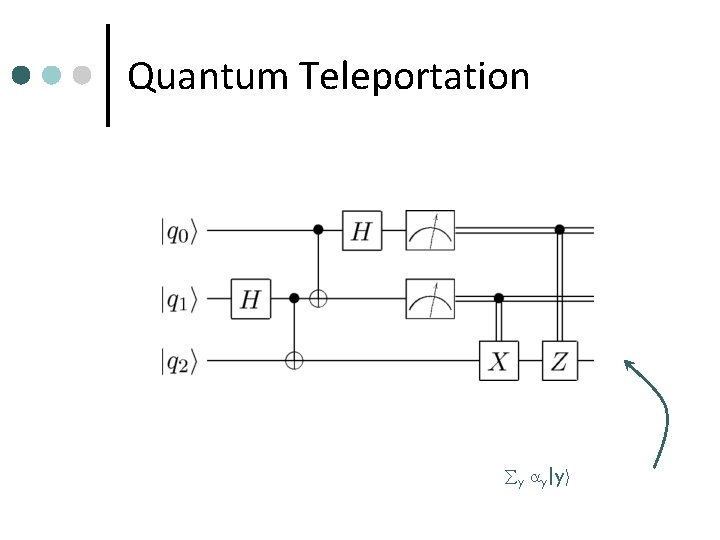
Quantum Teleportation ¢ ¢ ¢ ¢ Then: CNOT on q 0 and q 1 x=0, 1 x |xi y=0, 1 1/21/2|y, yi CNOT: x, y x/21/2 |x, x © y, yi Measure q 1: Result is a Prob. for 0/1 is 0. 5 each: | 0|2/2+| 1|2/2=1/2 Remaining state: y y©a |y © a , yi on q 0, q 2 Send a to Bob a=0 ) Bob does nothing a=1 ) Bob applies X-Gate (Bit Flip) Result in both cases: y y©a|y © a, y © ai = y y |y, yi

Quantum Teleportation ¢ ¢ State y y |y, yi Problem: Bob’s qubit q 2 is still entangled with q 0 y y |y, yi

Quantum Teleportation ¢ ¢ ¢ Alice applies H to q 0 Alice measures q 0, assume the result is b, she sends b to Bob Applying H: y y |y, yi 1/21/2 z, y y (-1)z¢ y |z, yi ¢ Measuring q 0 (Result is b; 0/1 with Prob. 1/2): y y (-1)b¢ y |yi on q 2 ¢ Bob corrects by applying a Z-Gate, if necessary

Quantum Teleportation y y|yi

Remarks ¢ ¢ ¢ The EPR-pair is consumed The original state | i is destroyed [no cloning!] States with many qubits can be teleported one by one (we need to make sure entanglement between the teleported qubits is preserved)