Quantum Computing Progress and Prospects Tony Hey and

Quantum Computing – Progress and Prospects Tony Hey and Douglas Ross University of Southampton

Plan of Lectures • Lecture #1: Introduction to Quantum Information Theory – Fundamentals (Tony Hey) • Lectures #2, 3 & 4: Quantum Algorithms in Detail – Bell States, Quantum Teleportation, Grover’s Quantum Search and Shor’s Quantum Factorization (Douglas Ross) • Lecture #5: Quantum Cryptography and Quantum Computing – State of the Art (Tony Hey)

Quantum Cryptography and Quantum Computing - State of the Art Tony Hey Director of e-Science EPSRC, Swindon Tony. Hey@epsrc. ac. uk

The Quantum Age “The nineteenth century was known as the machine age, the twentieth century will go down in history as the information age. I believe the twenty-first century will be the quantum age. ” Paul Davies 1996

Outline of Lecture • • • What is a Quantum Algorithm? Quantum Cryptography Quantum Computing Technologies Quantum Error Correction Experiments at Southampton Conclusions

What is a Quantum Algorithm? • Superposition is not specific to quantum mechanics • Can write 2 qubit Hadamard gate as 4 x 4 matrix acting on 4 -d column vectors representing (0, 0), (1, 0), (0, 1) and (1, 1) states Ø Implement 2 qubit Hadamard gate in conventional electronics with four input wires and four output wires Ø Logically reversible, no entanglement

An Electronic Analogue of Grover’s Quantum Search • Superposition not specifically quantum - entanglement and measurement are quantum specific • Without genuine multi-particle quantum entanglement see that we need number of wires to rise exponentially with the number of qubits for our electronic analogue simulation Ø Suspect that this is true more generally

Quantum Cryptography (1) • Application of Quantum Information rather than Quantum Computing • Not really Cryptography – Quantum Key Distribution would be better name • Describe one possible realization using photon polarizations as qubits • Nicholas Gisin and his group in Geneva are one of the leading players in this field

Quantum Cryptography (2) One-Time Pads • Most secure cryptosystem – encode each bit of message using different secret random number Encode: M = N + K modulo 2 Decode: M + K modulo 2 = N • Problem: both sender (Alice) and receiver (Bob) need to have copy of same set of keys that eavesdropper (Eve) does not have

Quantum Cryptography (3) • Giles Brassard and Charles Bennett proposed using qubits to exchange secret keys in 1984 • BB 84 Scheme uses polarization states of photon as qubit • Alice can send photons Either - in Horizontal-Vertical Basis with polarizers set at 0 and 90 degrees Or - in Diagonal Basis with polarizers set at 45 and 135 degrees

Quantum Cryptography (4) • Bob can also choose to receive photons either in H-V basis or in Diagonal basis – he does not know Alice’s settings in advance • If Alice sends a ‘ 1’ using H-V setting but Bob measures photon in Diagonal setting, Bob will measure a ‘ 1’ 50% of the time and a ‘ 0’ for the remaining 50% How does this help?

Quantum Cryptography (5) • After sending stream of bits in randomly chosen settings, Alice then telephones Bob and they agree which are the ‘good’ bits What use is this? • Suppose Eve is intercepting the bits from Alice and re-sending them on to Bob • Since Eve has to guess which setting Alice used (H-V or Diagonal) there is now a probability of ¼ for Alice and Bob to disagree on the bit sent even when they use the same settings

Quantum Cryptography (6) State of the Art • First demonstration system built by Charles Bennett at IBM in 1989 • Many groups now demonstrated real systems transmitting keys down commercial optical fibres over many kilometres e. g. Richard Hughes at LANL, Nicholas Gisin under Lake Geneva, Paul Townsend at BT • Hughes group also demonstrated free space transmission possible

Quantum Computing Technologies (1) Four essential requirements for quantum computational hardware: (1) Must be able to prepare multiple qubits in addressable form (2) Must be mechanism for performing quantum logic operations (3) Must be readout mechanism for each qubit at end of computation (4) System must be adequately isolated from environment for long enough to perform calculation

Quantum Computing Technologies (2) Ion Trap Computing Wineland: Hughes: Cavity QED Kimble: Haroche: CNOT gate with 2 Be ions cooled to vibrational ground state Addressed trapped Ca ions - sideband cooling ‘soon’ Conditional quantum dynamics with single atom & photon Successive atoms through cavity NMR ‘Ensemble’ Quantum Computing Chuang: Zurek: Jones: 3 qubit quantum gates using HCCI 3 (chloroform) GHZ 3 qubit state NMR realizations of Deutsch’s and Grover’s algorithms

Quantum Computing Technologies (3) What about quantum error correction? Ø Not only bit flips but also quantum phase changes Ø Caused by interactions with the environment - commonly referred to as ‘decoherence’ Surprisingly Shor and Steane showed that entanglement of extra bits allows error correction 1 qubit 7 qubits Sophisticated fault-tolerant schemes possible in principle

Quantum Computing Technologies (4) • To implement Shor’s algorithm to factorize l-bit number requires: # of qubits L = 5 l + 4 # of gates n. G = 25 l 3 + O(l 2) • For 130 digit number (432 bits) need: L = 2000 qubits and n. G = 109 gates • With a concatenated quantum error correction scheme Preskill estimates would require: L = 106 qubit system!

Southampton Quantum Technology Centre • Multi-disciplinary collaboration between physicists, computer scientists and electronic engineers • Southampton hosts dedicated Silicon Fabrication Facility funded by EPSRC – Silicon oxidation, implantation, diffusion doping, reactive etching – Si. Ge and selected metals, direct-write electron beam lithography

Southampton Quantum Technology Centre Facilities

Quantum Computing Technologies • Several groups pursuing ion traps and NMR technologies • Goal of Southampton effort is to build small-scale qubit devices in the solid state that can be easily integrated with conventional technologies – Self-assembled Quantum dots – Josephson Junction Qubits

Self-Assembled Ge/Si. Ge Quantum Dots • grown by MOCVD on Si substrates • 100 nm diameter x 50 nm high • Single dot spectroscopy • quantum devices functional Darren Bagnall and Jeremy Baumberg Si

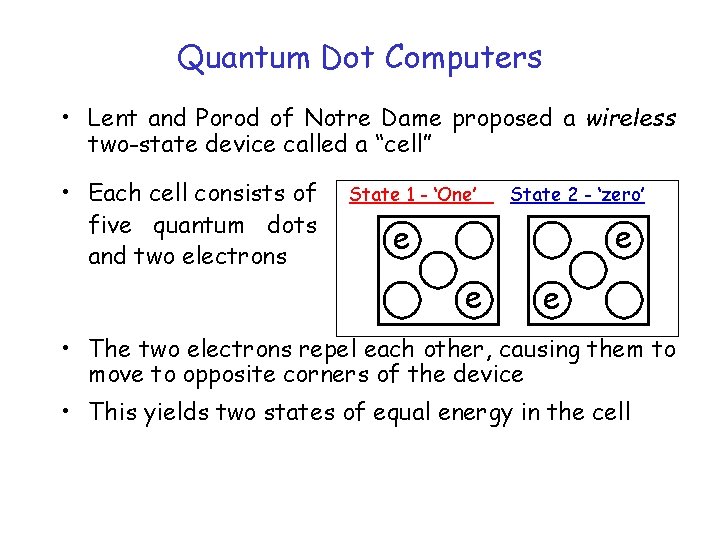
Quantum Dot Computers • Lent and Porod of Notre Dame proposed a wireless two-state device called a “cell” • Each cell consists of five quantum dots and two electrons State 1 - ‘One’ State 2 - ‘zero’ e e • The two electrons repel each other, causing them to move to opposite corners of the device • This yields two states of equal energy in the cell

NEC Press Release

Josephson Junction Qubits • Superconductors - paired electrons in macroscopic quantum state • Josephson effect - pair tunneling through insulator S I S Josephson Junction (JJ) • Combine JJs to form Single Electron Transistor (SET) or Superconducting Quantum Interference Devices (SQUID) • SETs or SQUIDs form basis for design of charge-coherent or phase-coherent fabrication qubits • Novel techniques with angled deposition

Josephson Junction Charge Qubit Peter De Groot and Adrian Potts

Conclusions? Feynman “not sure if there was a real problem with quantum mechanics” - “Squeeze the difficulty of quantum mechanics into a smaller and smaller place” Perhaps the foundation of a new multi-billion dollar industry!