Computer Security Quantum Cryptography including Quantum Communication Quantum

Computer Security “Quantum Cryptography” including Quantum Communication Quantum Computing Page 1

Quantum Communication NOT used to encrypt data! Goal, instead, is to detect eavesdroppers Can be used to exchange a private key Page 2

Uncertainty Principle In quantum mechanics, certain pairs of properties of particles cannot both be known simultaneously, e. g. , – Position and momentum of an electron (Heisenberg) If a measurement determines (with precision) the value of one of the properties, then the value of the other cannot be known Page 3

Photon Spin (Polarization) Photons can be given either “rectilinear’’ or “diagonal’’ spin as they travel down a fiber. Rectilinear: or Diagonal: or Measuring rectilinear spin with a rectilinear filter yields polarization of photon. blocked Page 4

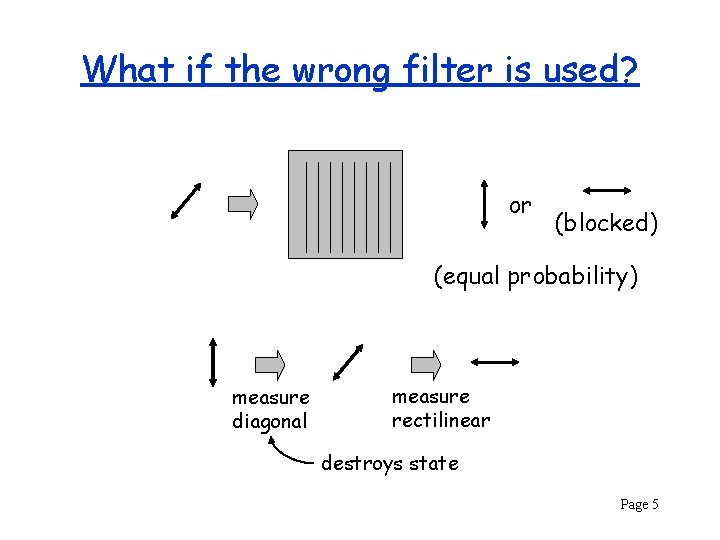
What if the wrong filter is used? or (blocked) (equal probability) measure diagonal measure rectilinear destroys state Page 5

Quantum Key Exchange The goal is to enable Alice and Bob to agree on a private key, even in the face of an eavesdropper, Eve. Like Diffie-Hellman, the protocol is still susceptible to a “man-in-the-middle” attack. But unlike Diffie-Hellman, the protocol does not depend on the difficulty of computing discrete logarithms or any other computational problem. Page 6

BB 84 Protocol (Bennet and Brassard) 1. Alice sends Bob a stream of photons randomly polarized in one of 4 polarizations: bit encoding: 0 1 2. Bob measures the photons in random orientations e. g. : x++xxx+x (orientations used) | - / / - (measured polarizations) 1 0 1 1 0 0 1 1 (encoded bit values) 3. Bob tells Alice in the open what orientations he used, but not what bit values he measured 4. Alice sends Bob in the open a list of positions at which the orientations are correct Page 7

Detecting an Eavesdropper Alice selects some subset of k of the shared bits and reveals them to Bob in the open. If Bob notices any differences, then Eve must have changed a bit by guessing the wrong polarization when eavesdropping. Eve has little hope of guessing the same polarization as Bob all k times. Each measurement has a ¼ chance of changing a bit value. The probability of not changing any values is (3/4)k – which can be very small if k is chosen large enough Page 8

In the “real world” In April 2014 China began installing a 2000 -kilometer quantum communications link between Beijing and Shanghai In August 2016 China launched the Quantum Science Satellite (QUESS) and plans to test quantum entanglement over large distances, and quantum key exchange Page 9

Quantum Computers The state of a computer consists of the contents of its memory and storage, including values of registers (including the program counter), memory, disk contents, etc. In a conventional computer each memory “unit” holds one value (e. g. , 0 or 1) at a time. Computation consists of a sequence of state transitions. But in a quantum computer, a memory unit holds a “superposition” of possible values. Page 10

Qubit (somewhat simplified) A single quantum “bit” which is 1 with probability p and 0 with probability 1 -p. When measured, outcome is either 0 or 1. Measuring a qubit changes its value! If outcome is 0, p is set to 0, if outcome is 1, p is set to 1. A qubit could be implemented using a photon to carry a horizontal or vertical polarization. Page 11

Quantum Entanglement Suppose two bits have value 00 with probability ½ and 11 with probability ½. If the bits are separated and measured at different locations, the measurements must yield the same values. E. g. , if first measurement is 0, second must also be 0. Entanglement also allows multiple states (e. g. , 00 vs. 11) to be acted on simultaneously. Difficulty in building a quantum computer is maintaining quantum entanglement in the face of environmental noise (quantum decoherence). Page 12

More on Qubits A qubit is a superposition of two basis states, and (representing values 0 and 1), which can be thought of as north and south poles of a unit sphere. https: //commons. wikimedia. org/wiki/File: Bloch_sphere. svg I. e. , qubit is , where v 0 and v 1 are complex numbers such that |v 0|2 + |v 1|2 = 1. (|v 0|2 and |v 1|2 are probabilities of qubit being 0 or 1) can be written as Page 13

Quantum Gates Qubits are manipulated with quantum logic gates. Gates are just multiplications by unitary matrices. Hadamard matrix i. e. , gate operation is maps to and This gate randomizes a basis state to have equal chance of being measured 0 or 1. to Page 14

Factoring Large Primes In 1994 Peter Shor showed that a quantum computer can factor a number n in O(log 3 n) time. A similar result holds for solving the discrete logarithm problem. If a large-enough quantum computer can be built, then RSA and Diffie-Hellman key-exchange will no longer be secure. (But largest number factored with this algorithm as of 2015 was 21!) Page 15

Details of Shor’s Algorithm 1. Pick a random number 1 < a < n 2. If a is a factor of n (i. e. , GCD(a, n) > 1), what a lucky guess! 3. Use a quantum circuit to find smallest r > 1 such that ar = 1 mod n, i. e. , find the order of a 4. If r is odd go back to step 1 5. If ar/2 = -1 mod n go back to step 1 6. GCD(ar/2 + 1, n) and GCD(ar/2 - 1, n) are factors of n Example: n = 15, a = 7, r = 4 a 1 = 7 mod n, a 2 = 4 mod n, a 3 = 13 mod n, a 4 = 1 mod n a 4/2+1 = 50, a 4/2 -1 = 48 GCD(50, 15) = 5, GCD(48, 15) = 3 Page 16

Analysis of Shor’s Algorithm Reduces factoring to order finding. Uses quantum computation to solve order finding. After step 4, r is even, ar/2 ≠ 1 mod n. Proof: Otherwise r was not smallest positive integer such that ar = 1 mod n. Thus ar/2 - 1 ≠ 0 mod n. After step 5, ar/2 ≠ -1 mod n. Thus ar/2 + 1 ≠ 0 mod n. Observe that (ar/2 - 1) (ar/2 + 1) = ar – 1 = 0 mod n So (ar/2 - 1) (ar/2 + 1) = kn for some integer k. But neither (ar/2 - 1) or (ar/2 + 1) is a multiple of n. Therefore by the prime factorization theorem, one contains p and the other contains q. Page 17

Analysis of Shor’s Algorithm What is the probability that if a is chosen at random in step 1, r (the order of a) is odd? Claim: If the order of a is odd, the order of –a is even. Proof: Let r’ be the order of –a, and suppose r’ is odd. Then ar’=(-1*-a)r’=-1*(-a)r’=-1 mod n. If r’ < r, then the order of a is r=2 r’, and hence r is even, a contradiction. If r’ > r, then (-a)r=-1 mod n, so r’ = 2 r, and hence r’ is even, another contradiction. Thus at most half of the elements between 2 and n-1 have odd order. Page 18

Controversial Quantum Computer D-Wave Systems, Inc. , purports to build a quantum computer based on a 128 -qubit chipset. No convincing demonstration of speed-up over conventional computer yet. Unresolved debate about whethere is actually quantum entanglement among the qubits. (Evidence seems to be leaning towards yes? ) Page 19