BOOLEAN ALGEBRA Boolean Algebra 1 BOOLEAN ALGEBRA REVIEW

BOOLEAN ALGEBRA Boolean Algebra 1

BOOLEAN ALGEBRA -REVIEW Boolean Algebra was proposed by George Boole in 1853. Basically AND, OR NOT can be expressed as Venn Diagrams Boolean Algebra 2

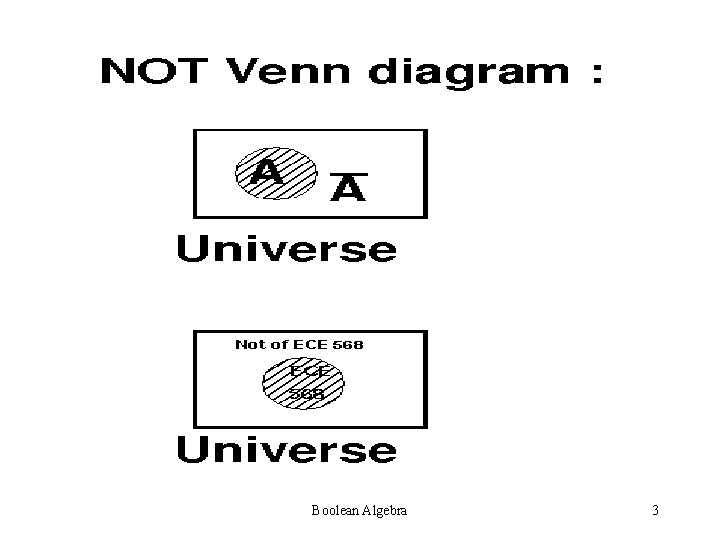
Boolean Algebra 3

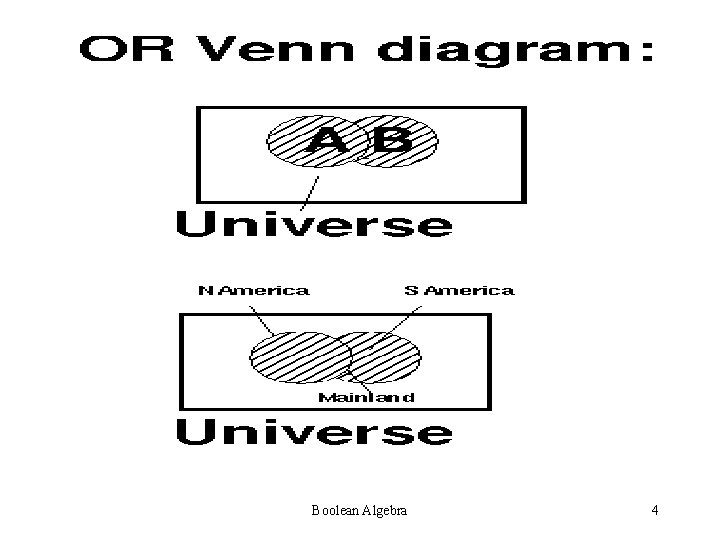
Boolean Algebra 4

Boolean Algebra 5

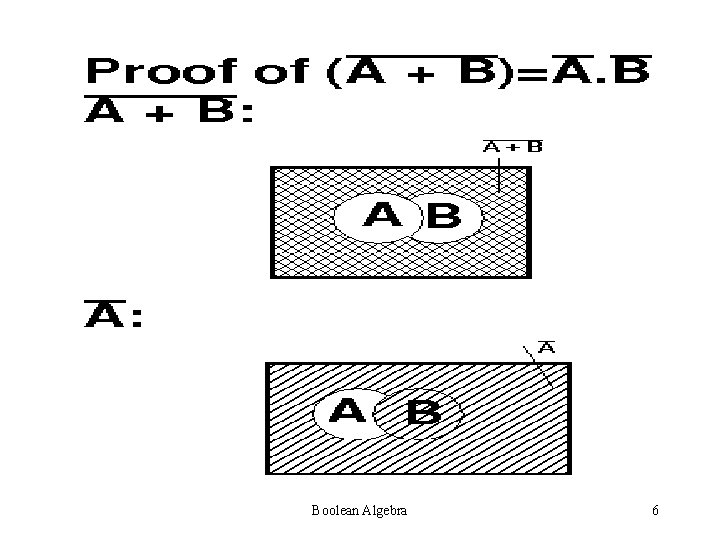
Boolean Algebra 6

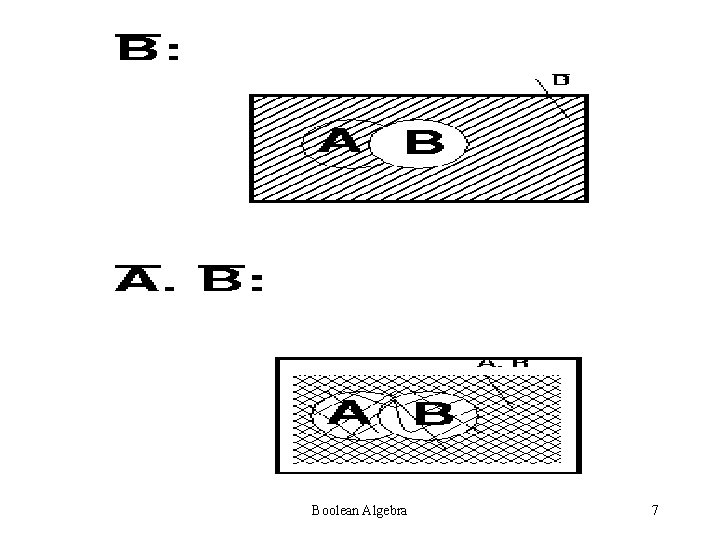
Boolean Algebra 7

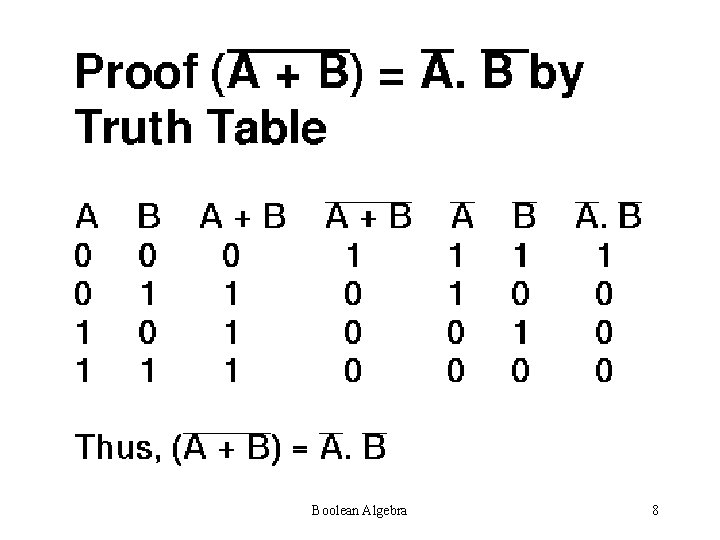
Boolean Algebra 8

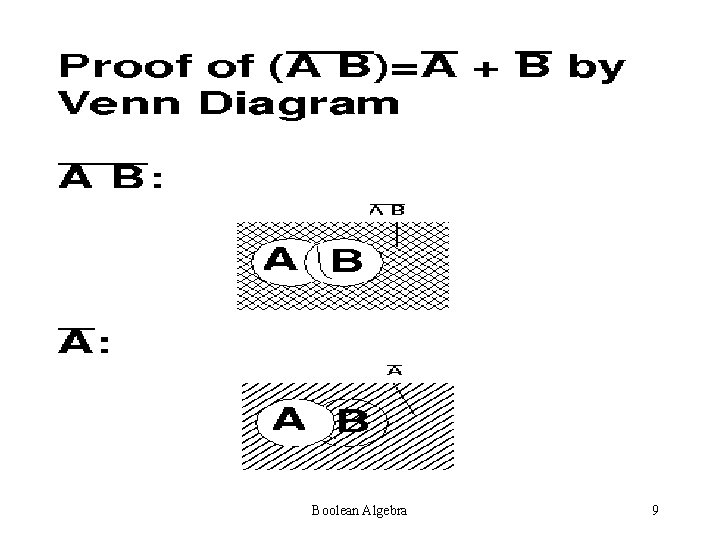
Boolean Algebra 9

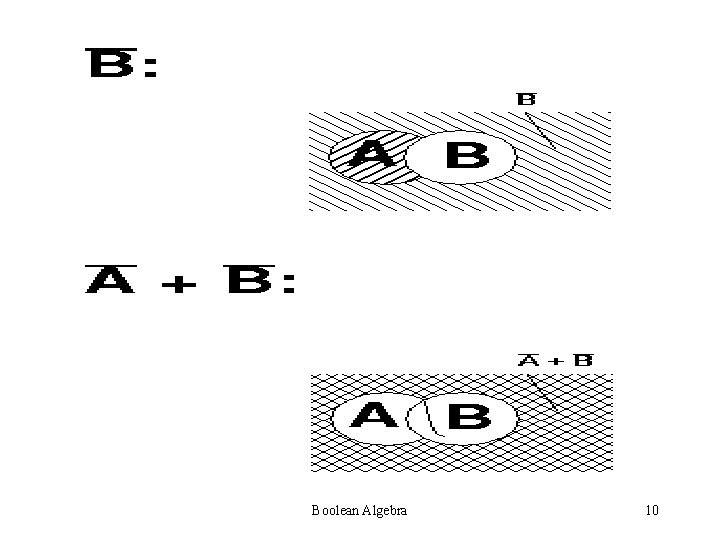
Boolean Algebra 10

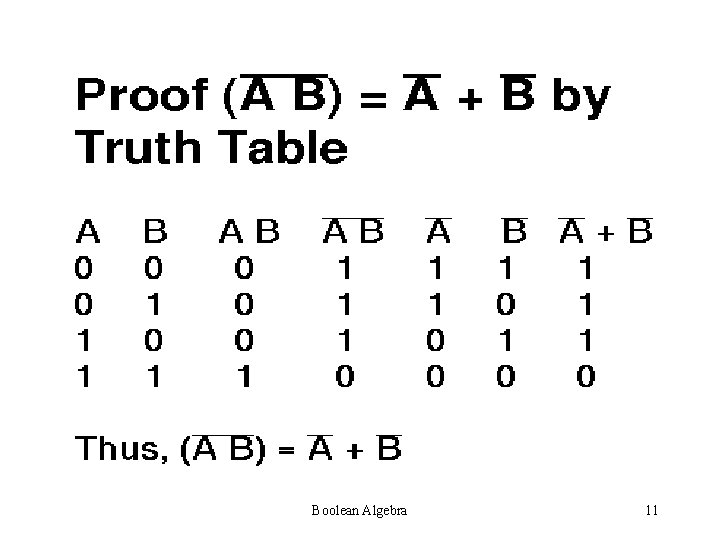
Boolean Algebra 11

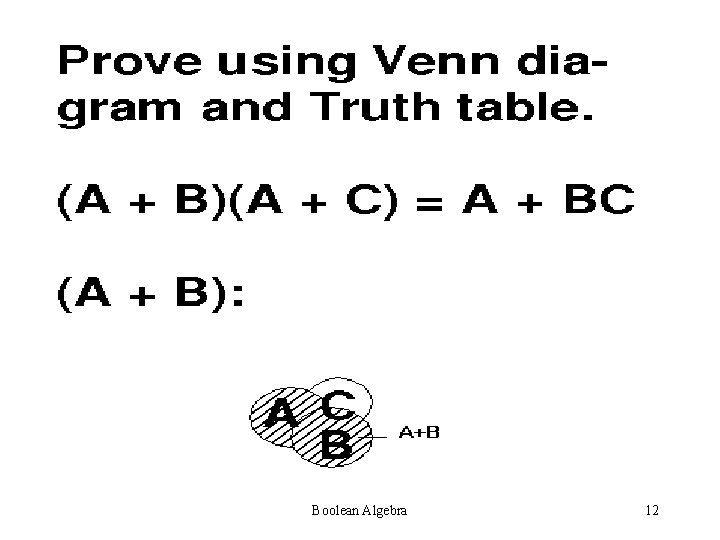
Boolean Algebra 12

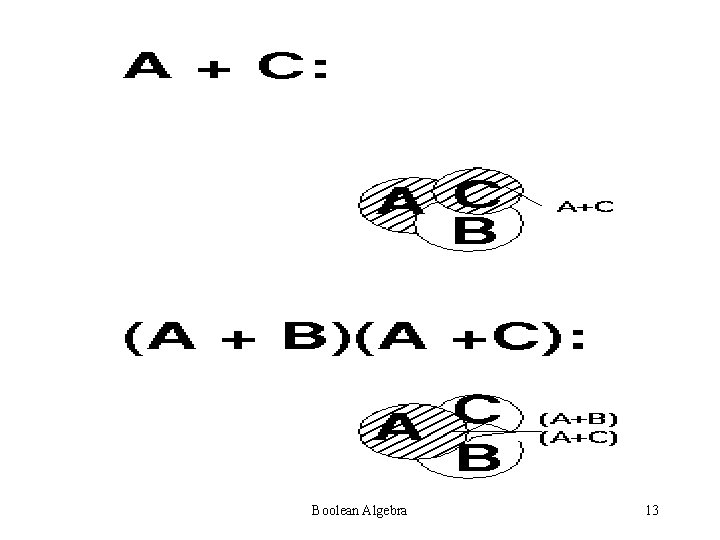
Boolean Algebra 13

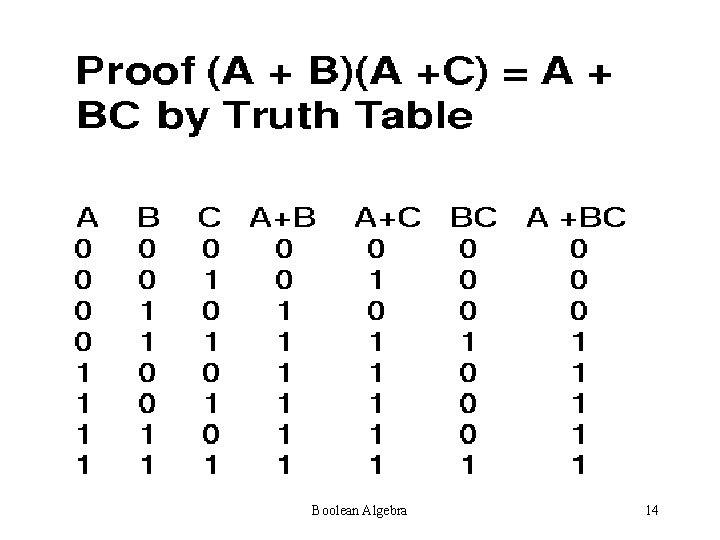
Boolean Algebra 14

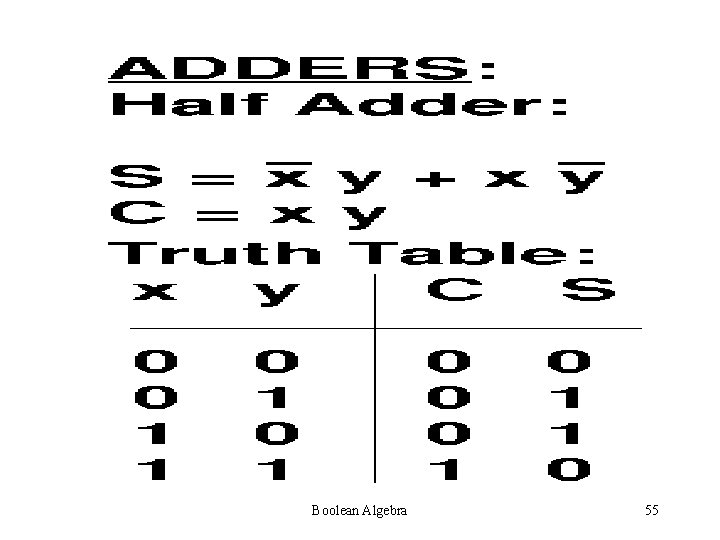
Min Terms and Max Terms Min Terms are those which occupy minimum area on Venn Diagram Max Terms are those which occupy maximum area on Venn diagram. Boolean Algebra 15

Boolean Algebra 16

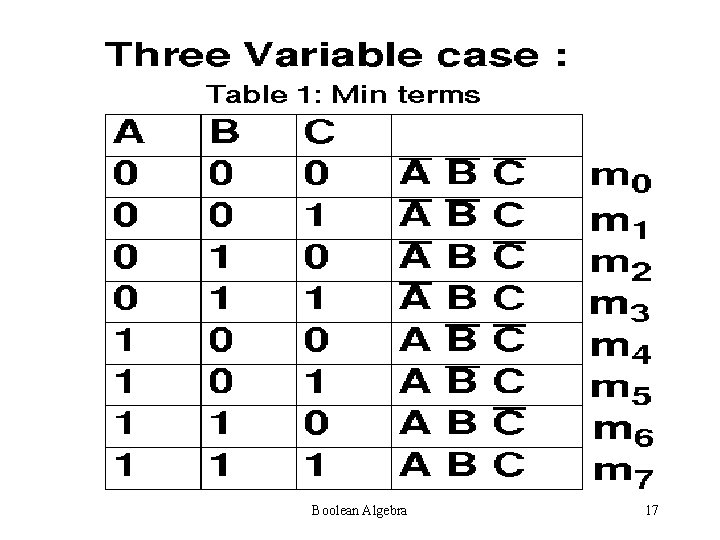
Boolean Algebra 17

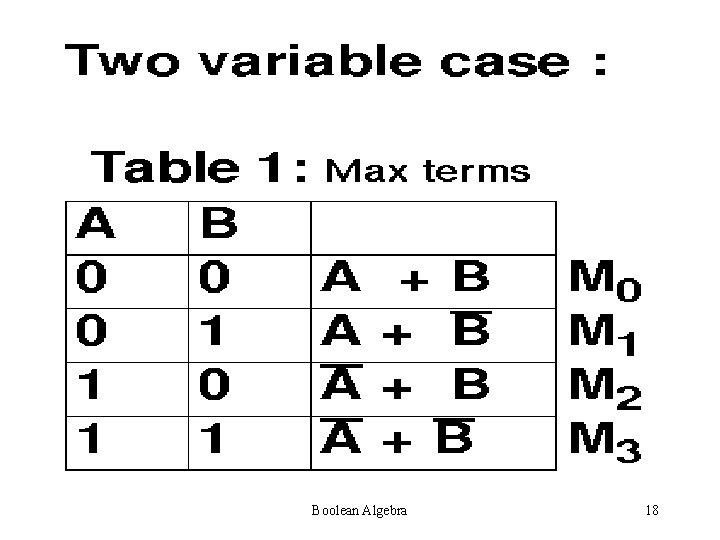
Boolean Algebra 18

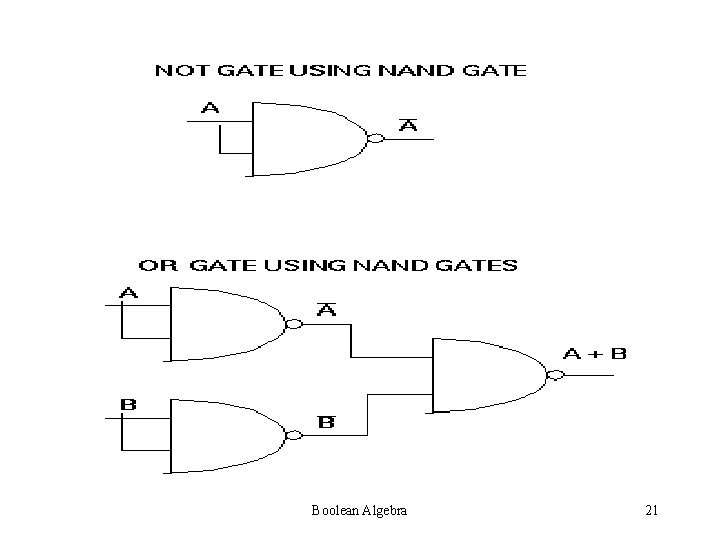
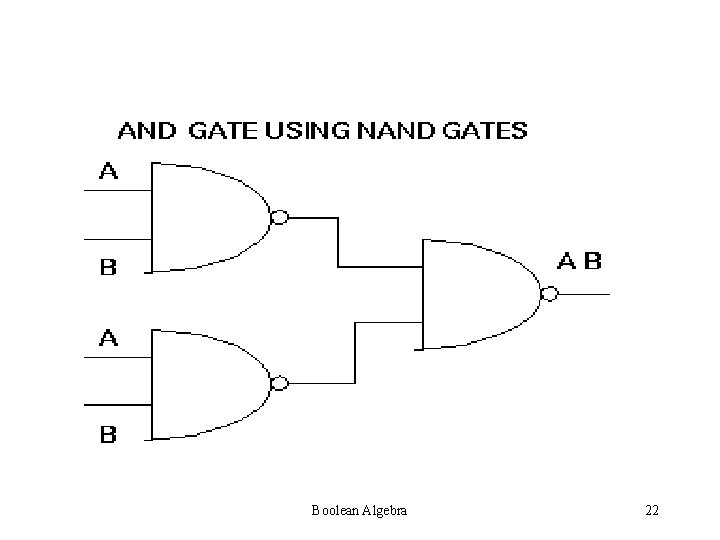
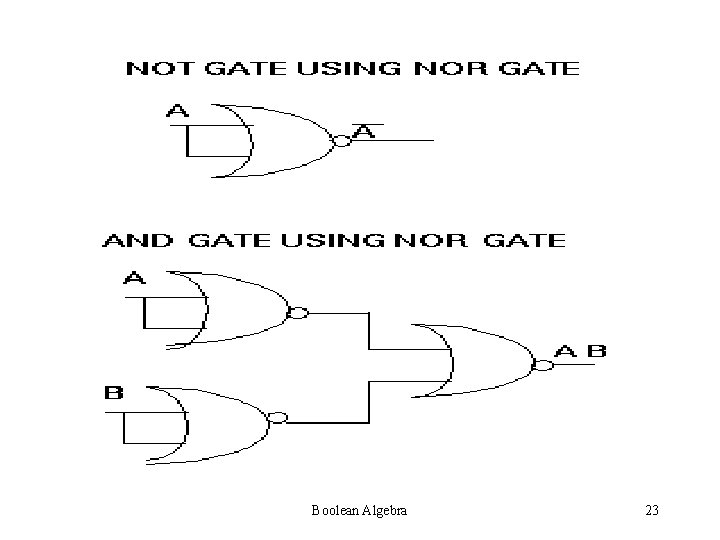
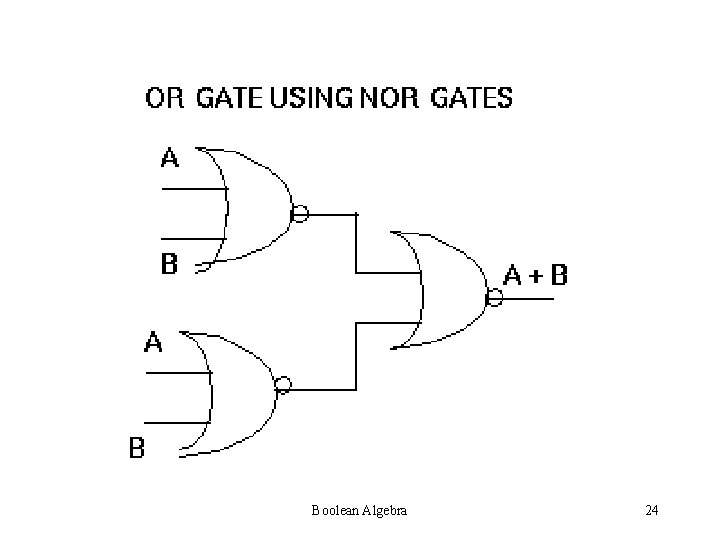
LOGIC GATES Nand Nor gates are called Universal gates as any Boolean function can be realized with the help of Nand Nor gates only Boolean Algebra 19

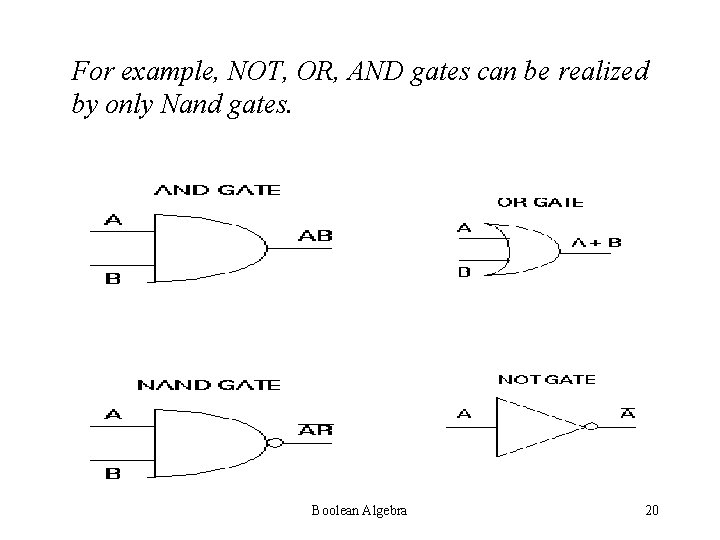
For example, NOT, OR, AND gates can be realized by only Nand gates. Boolean Algebra 20

Boolean Algebra 21

Boolean Algebra 22

Boolean Algebra 23

Boolean Algebra 24

SIMPLIFICATION OF BOOLEAN FUNCTIONS • • Algebraic Method Tabular Method K-Map Method Schienman Method Boolean Algebra 25

ALGEBRAIC METHOD Simplify using algebraic theorems Advantage: First Method based on Boolean Algebra theorems Disadvantage: No Suitable algorithm to apply (Trial type of method) Boolean Algebra 26

TABULAR METHOD Also called Quine Mc. Clusky Method Advantage: It may work for any no. of variables Disadvantage: Simplification from table is quite involved Boolean Algebra 27

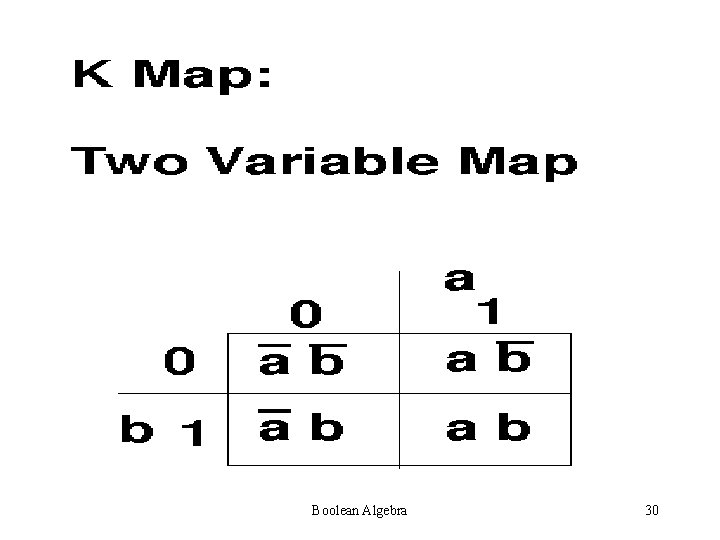
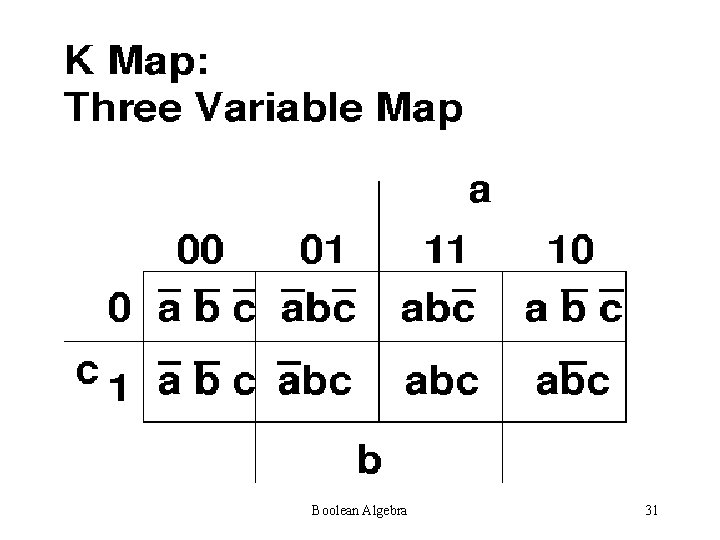
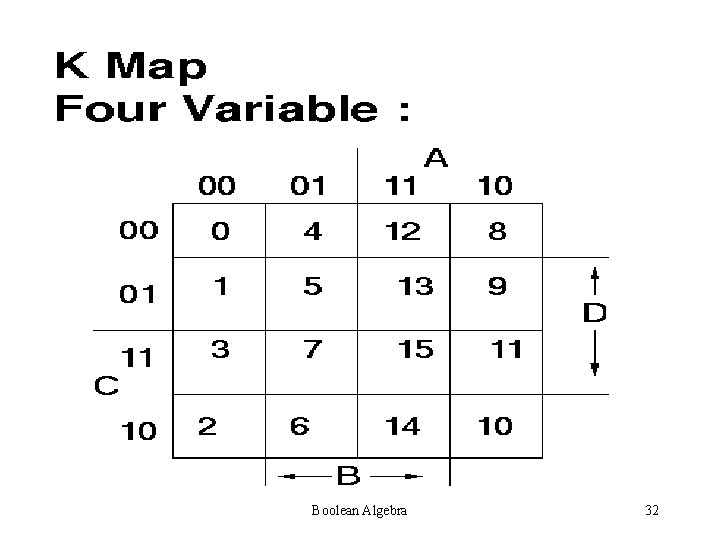
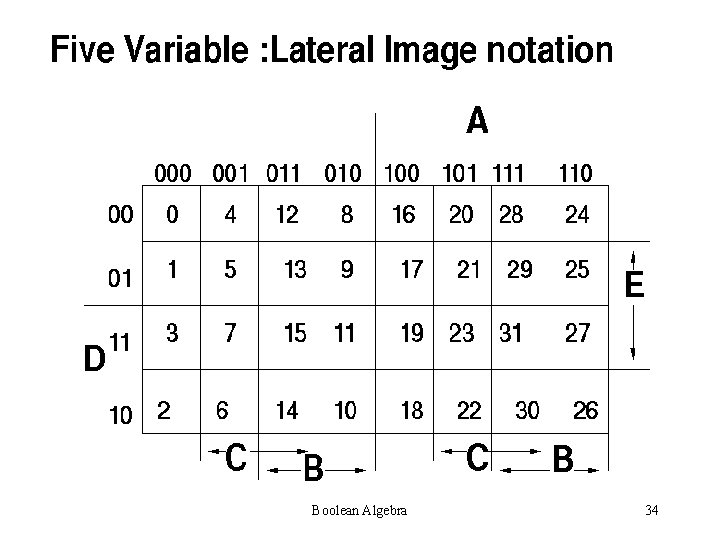
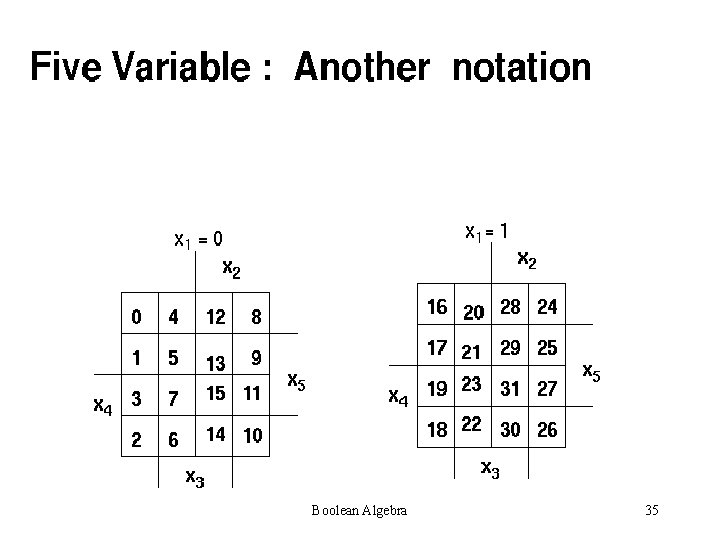
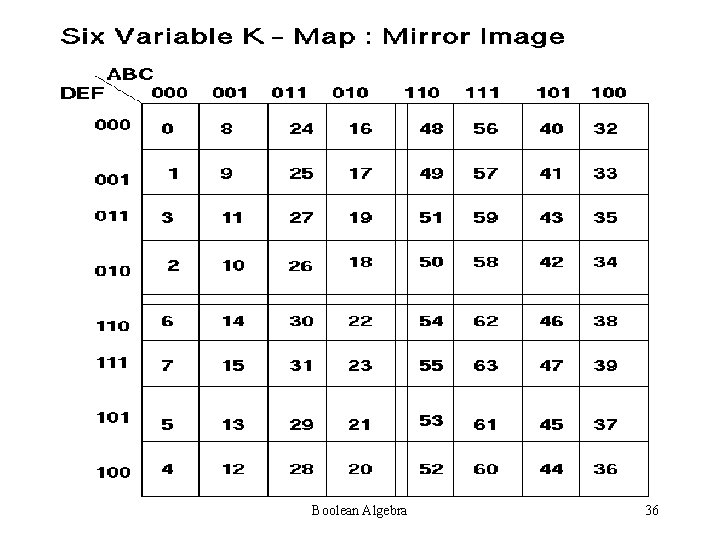
K-MAP METHOD Karnaugh Map. Also called Vietch Karnaugh Method. Advantage: Simplest and Widely accepted Disadvantage: Applicable for only upto Six variables Boolean Algebra 28

SCHIENMAN METHOD Columnwise writing of minterms as decimal numbers and their simplification Advantage: Very suitable for computerization. Applicable for any number of variables. Parallel Processing Disadvantage: May not result in most simplified answer for some problems Boolean Algebra 29

Boolean Algebra 30

Boolean Algebra 31

Boolean Algebra 32

Boolean Algebra 33

Boolean Algebra 34

Boolean Algebra 35

Boolean Algebra 36

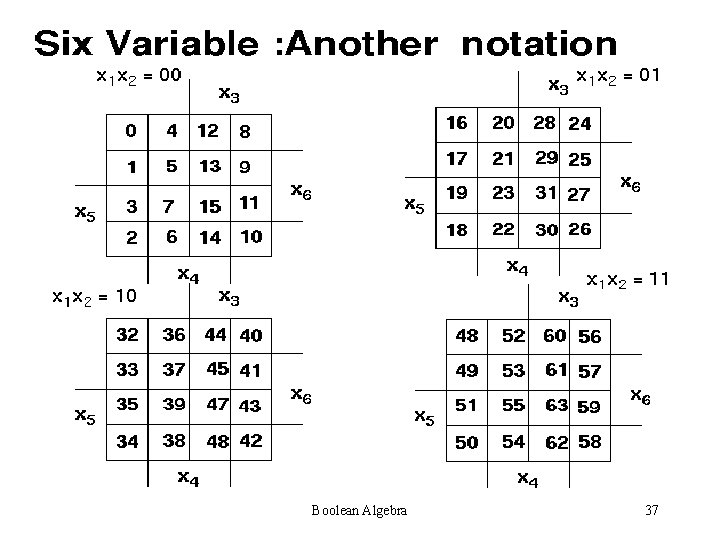
Boolean Algebra 37

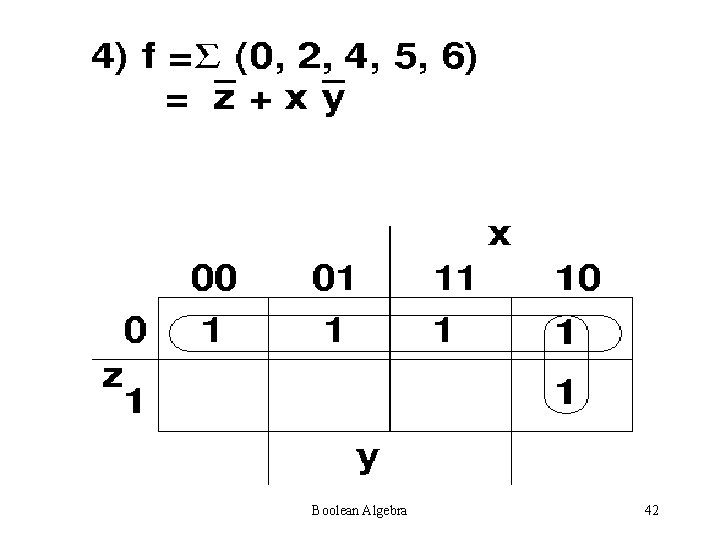
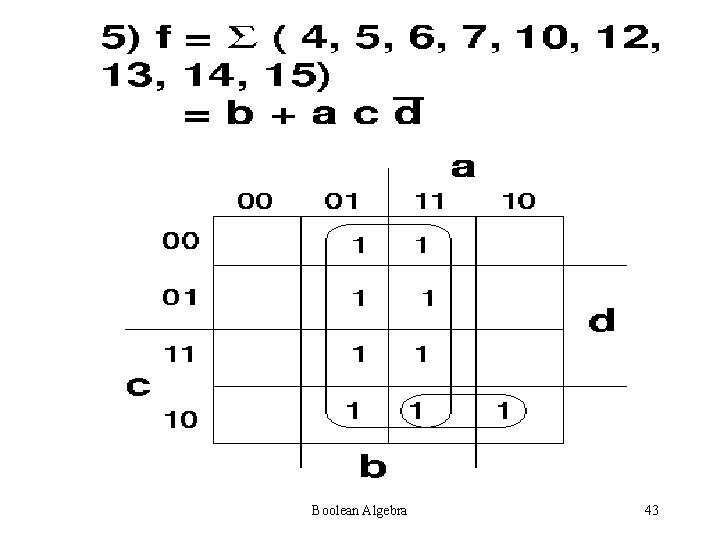
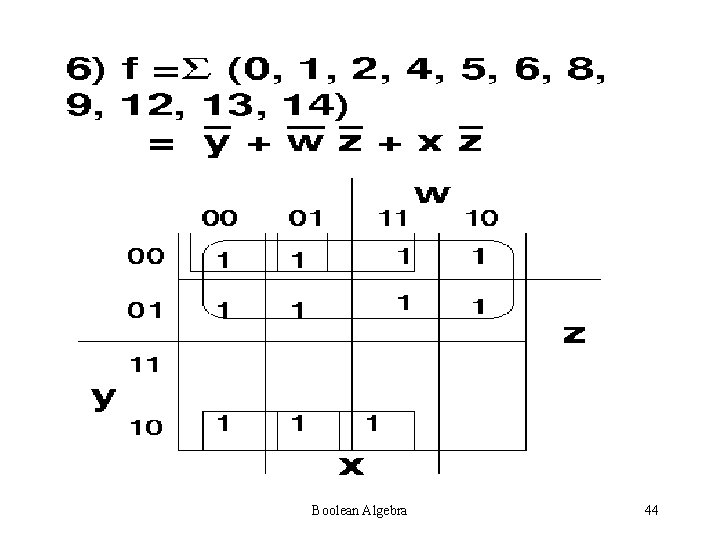
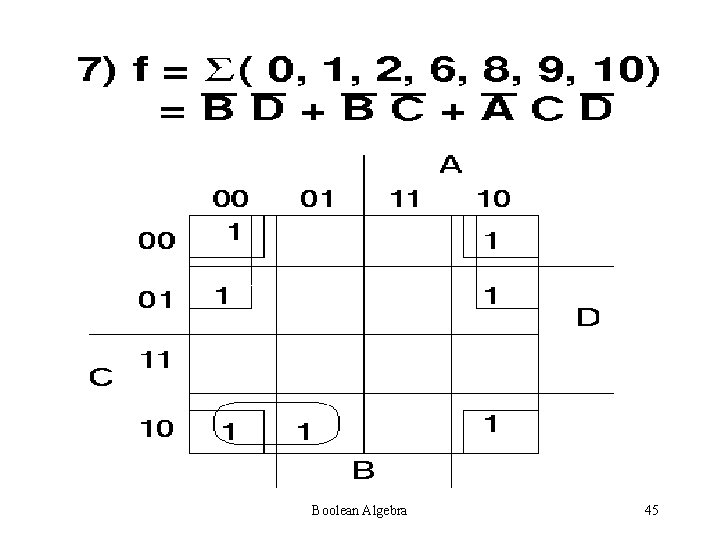
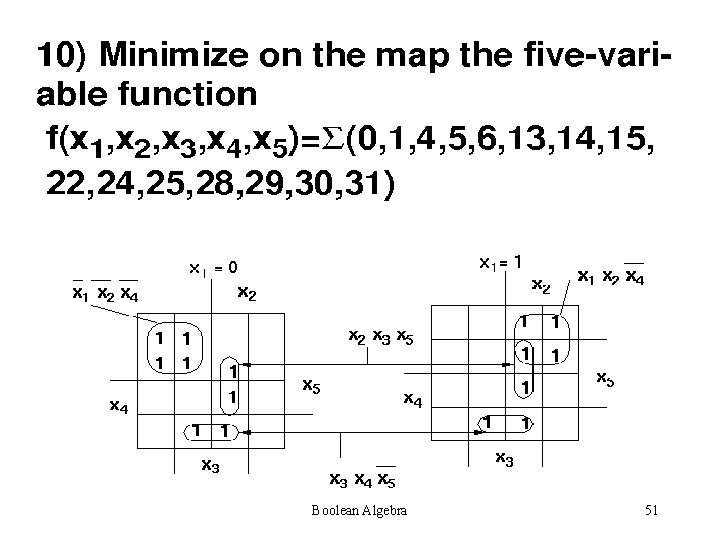
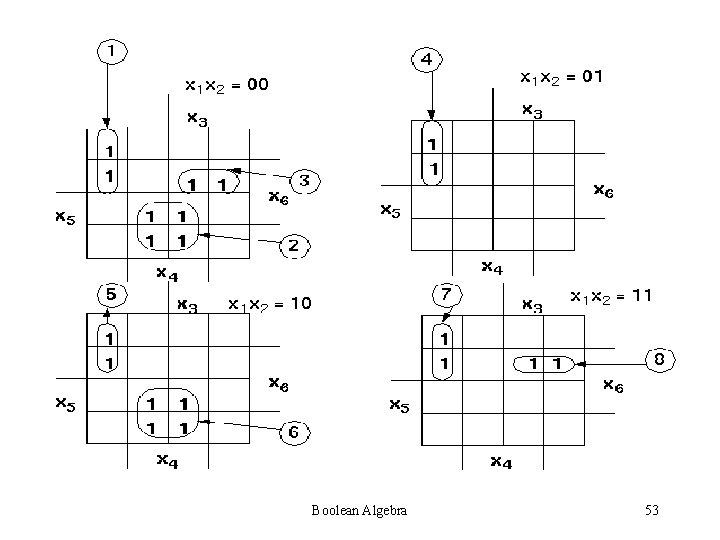
Steps for simplification: • Try to find single one’s – 2 one’s – 4 one’s – 8 one’s Always see is a higher combination exists. If a higher combination exists, wait. Be sure that you have managed the lower combination first. Boolean Algebra 38

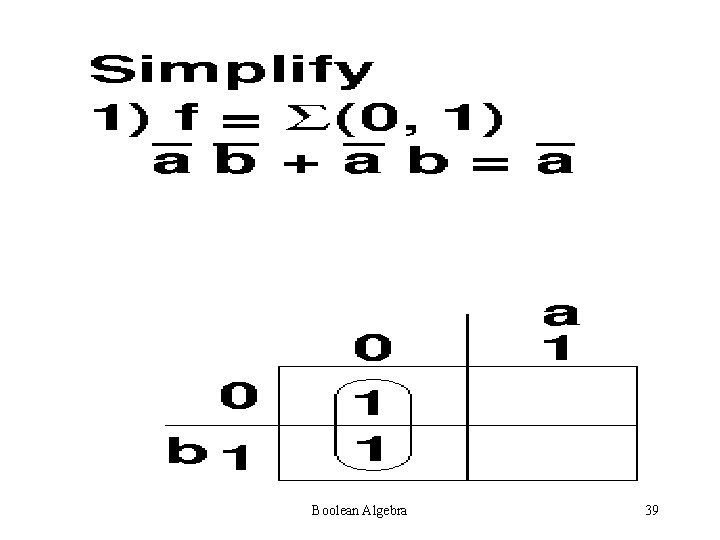
Boolean Algebra 39

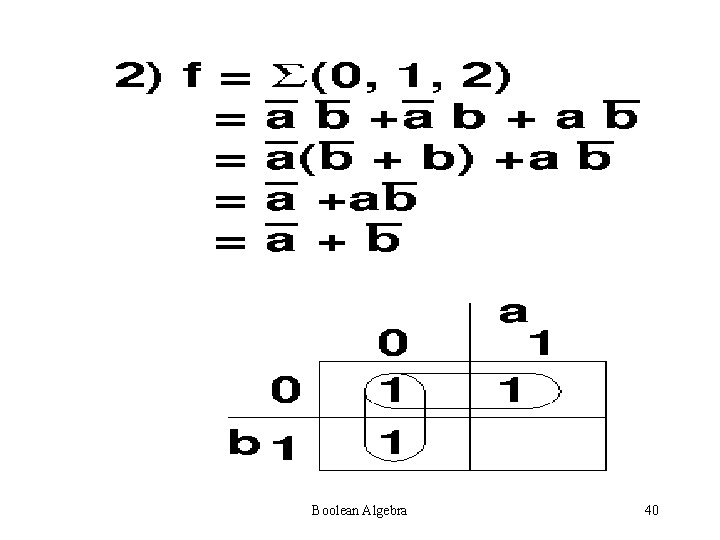
Boolean Algebra 40

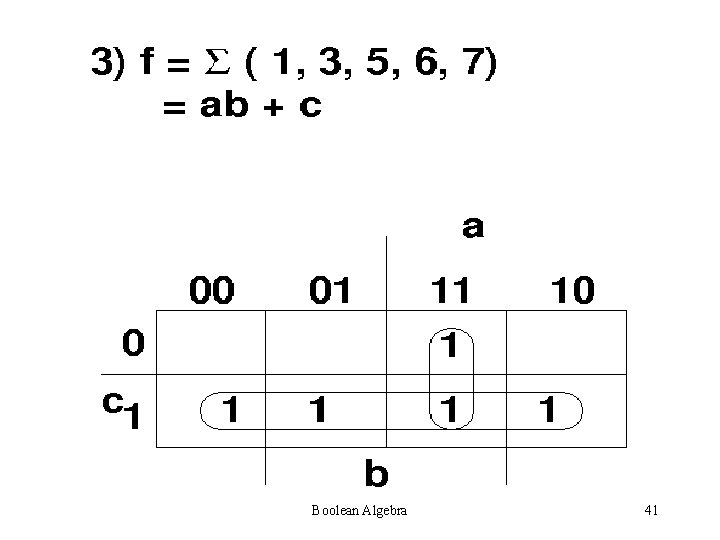
Boolean Algebra 41

Boolean Algebra 42

Boolean Algebra 43

Boolean Algebra 44

Boolean Algebra 45

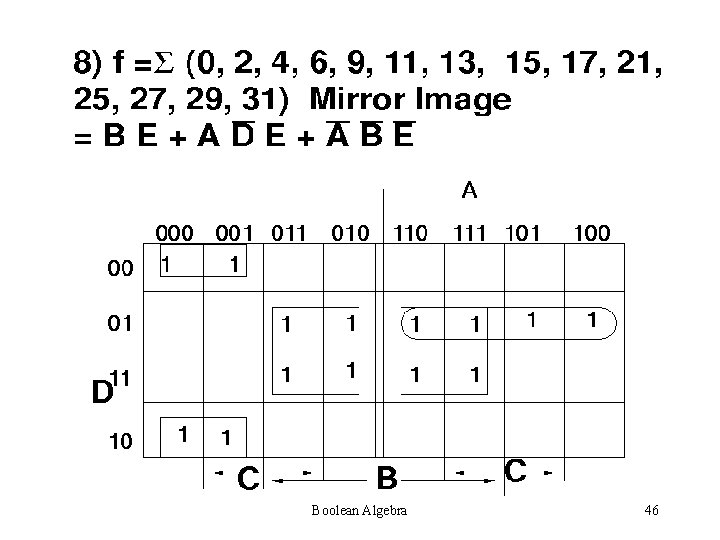
Boolean Algebra 46

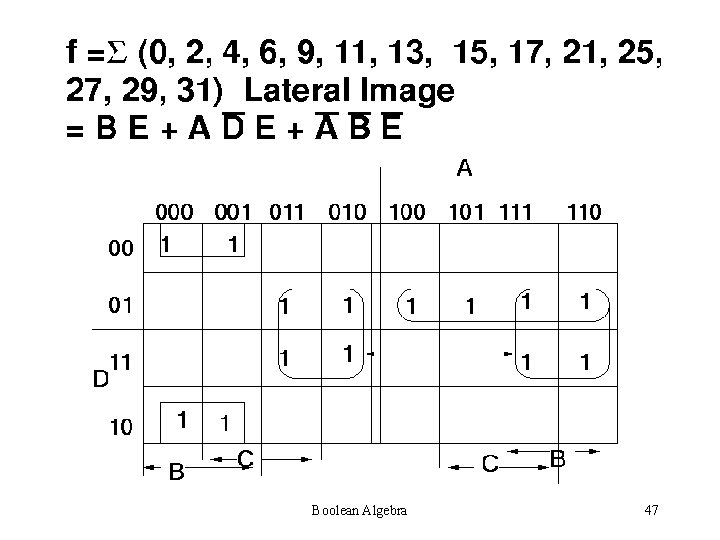
Boolean Algebra 47

Boolean Algebra 48

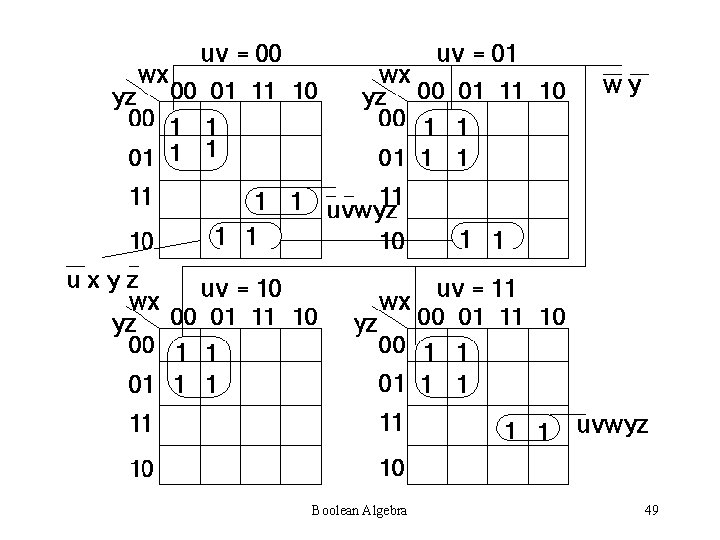
Boolean Algebra 49

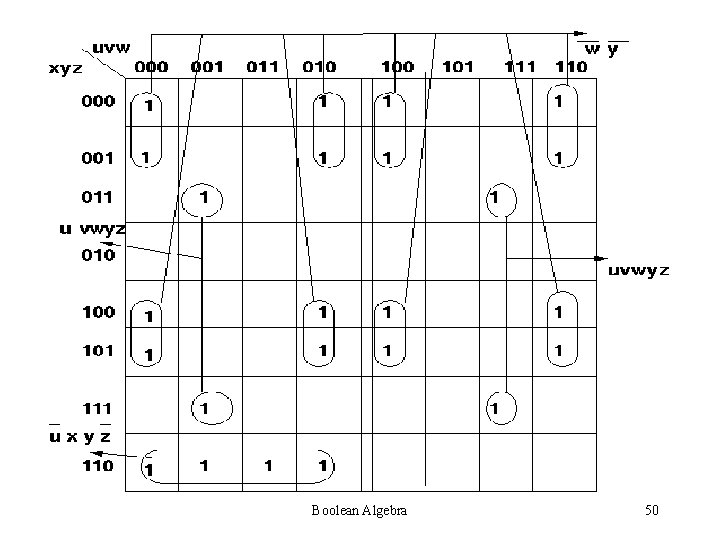
Boolean Algebra 50

Boolean Algebra 51

Boolean Algebra 52

Boolean Algebra 53

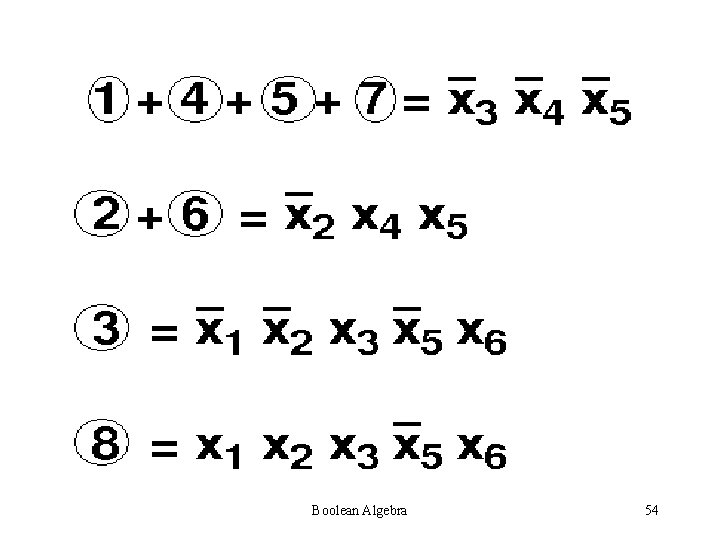
Boolean Algebra 54

Boolean Algebra 55

Boolean Algebra 56

Boolean Algebra 57

Boolean Algebra 58

SYMMETRIC FUNCTIONS • DEFINITION • PROPERTIES • IDENTIFICATION Boolean Algebra 59

Definition A switching function of n variables f(X 1, X 2…. Xn) is called a symmetric (or totally symmetric), if and only if it is invariant under any permutation of its variables. It is partially symmetric in the variables Xi, Xj where {Xi, Xj} is a subset of {X 1, X 2…Xn} if and only if the interchange of the variables Xi, Xj leaves the function unchanged. Boolean Algebra 60

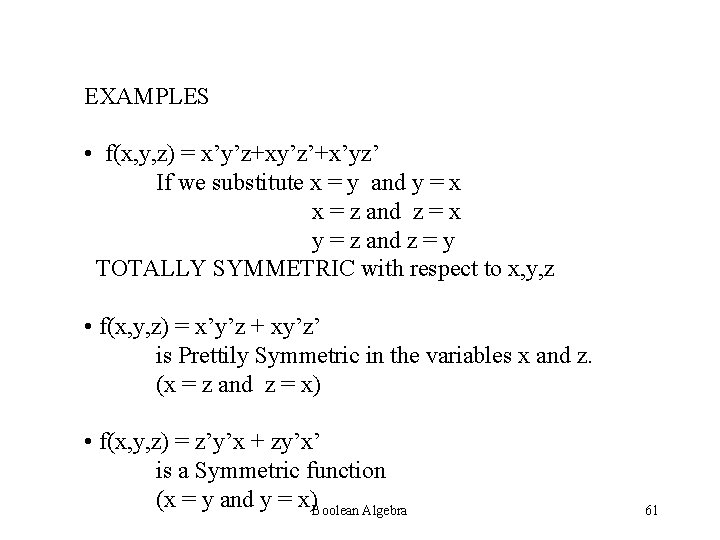
EXAMPLES • f(x, y, z) = x’y’z+xy’z’+x’yz’ If we substitute x = y and y = x x = z and z = x y = z and z = y TOTALLY SYMMETRIC with respect to x, y, z • f(x, y, z) = x’y’z + xy’z’ is Prettily Symmetric in the variables x and z. (x = z and z = x) • f(x, y, z) = z’y’x + zy’x’ is a Symmetric function (x = y and y = x)Boolean Algebra 61

• f(x, y, z) = y’x’z +yx’z’) is Not a Symmetric function This function is symmetric w. r. t x and z, but not symmetric w. r. t x and y. So Partially Symmetric • f(x 1, x 2, x 3) = x 1’x 2’x 3’ + x 1 x 2’x 3+ x 1’x 2 x 3 is not symmetric w. r. t. the variables x 1, x 2, x 3, but is symmetric w. r. t the variables x 1, x 2, x 3’ >> f is not invariant under an interchange of variables x 1, x 3. That is, x 3’x 2’x 1’+x 3 x 2’x 1 +x 3’x 2 x 1 != f >> But f is invariant under an interchange of variables x 1, x 3’ That is, x 3 x 2’x 1 + x 3’x 2’x 1 + x 3 x 2 x 1’ = f So f is symmetric w. r. t the variables x 1, x 2 and x 3’ Boolean Algebra 62

The variables in which a function is symmetric are called the VARIABLES OF SYMMETRY Boolean Algebra 63

Necessary and Sufficient condition for function f(x 1, x 2…. xn) to be symmetric is that it may be specified by a set of numbers {a 1, a 2…ak} where 0<an<n, such that it assumes the value 1 when and only when ai of the variables are equal to 1. The numbers in the set are called the a-numbers Boolean Algebra 64

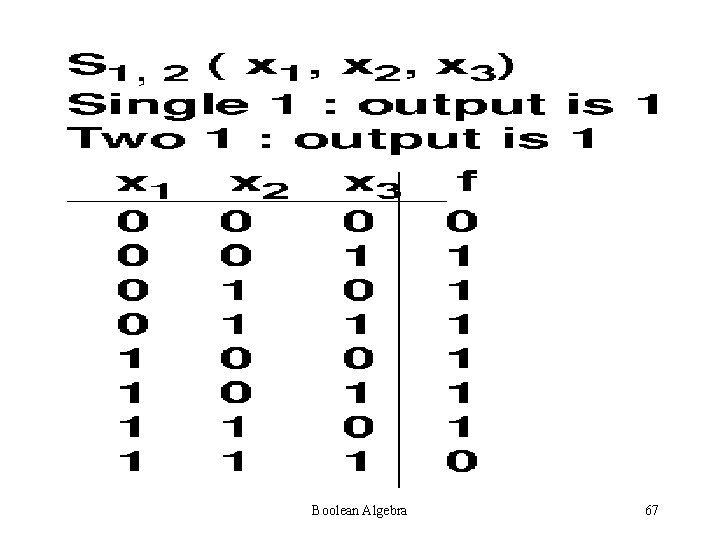
A Symmetric function is denoted by Sa 1, a 2…ak (x 1, x 2…. xn), where S designates the property of symmetry, the subscripts designate the a numbers, and (x 1, x 2…. xn) designate the variables of symmetry. Boolean Algebra 65

Boolean Algebra 66

Boolean Algebra 67

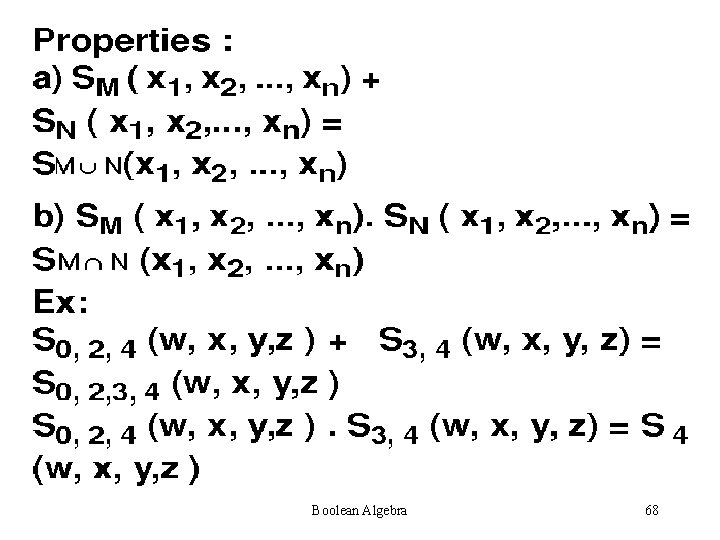
Boolean Algebra 68

Boolean Algebra 69

IDENTIFICATION The switching function to be tested for symmetry is written as a table in which all the minterms contained in the function are listed by their binary representation Boolean Algebra 70

For example, the function f(x, y, z) = å(1, 2, 4, 7) is written as shown: x y z a# The arithmetic sum of each 0 0 1 1 column in the table is computed 0 1 written under the column. This 1 0 0 1 sum is referred to as a column 1 1 1 3 sum. The number of 1’s in each 2 2 2 row is written in the corresp. position in column a#. This no. is called ROW SUM. Boolean Algebra 71

If an n-variable function is symmetric and one of its row sums is equal to some number a, then, by definition, there must exist n!/(n-a)!a! rows which have the same row sum. If all the rows occur the required number of times, then all colums sums are identical Boolean Algebra 72

For the example, all column sums equal 2, and there are two row sums, 1 and 3, that must be checked for “Sufficient Occurrence”. >> 3!/(3 -1)! = 3 ; 3!/(3 -3)! = 1 Both row sums occur the required number of times. Therefore, the function is symmetric and can be expressed by S 1, 3(x, y, z). Boolean Algebra 73

Boolean Algebra 74

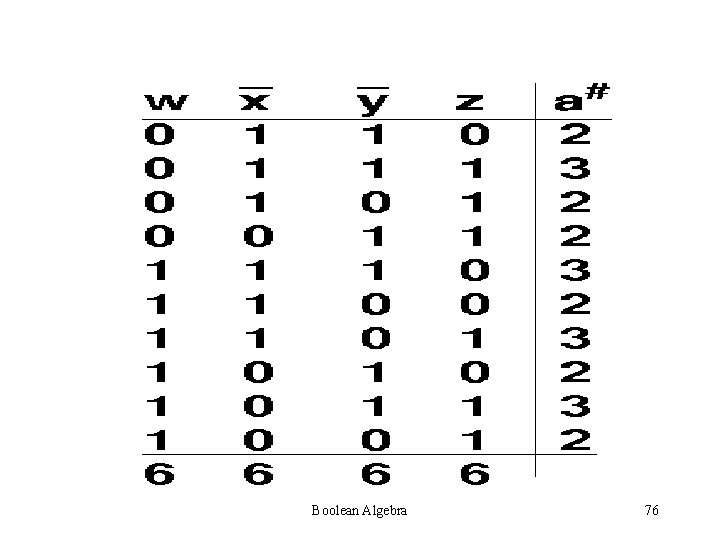
The column sums are 6 4 4 6 Since the column sums are not all the same, further tests must be performed to determine if the function is symmetric, and if it is, to find its variables of symmetry. The column sums can be made the same by complementing the columns corresponding to variables x and y. Boolean Algebra 75

Boolean Algebra 76

The new column sums are now computed and are found identical. The row sums are determined next and entered as a#. Each row sum is tested by the binomial co-efficient occurrence. 4!/(4 -2)! = 6 ; 4! /(4 -3)!3! = 4 Since, all row sums occur the required number of times, the function is symmetric, its variables of summetry are w, x’, y’, z and its a numbers are 2 and 3. ( f = S 2, 3(w, x’, y’, z)) Boolean Algebra 77

If columns w and z are complimented, instead of x and y, the table shown below results and since all its row sums occur the required no. of times, f can be written as f = S 1, 2(w’, x, y, z’) Boolean Algebra 78

Boolean Algebra 79

The column sums are all identical, but row sum 2 does not occur six times as required. One way to overcome this difficulty is by expanding the function about any one of its variables Boolean Algebra 80

The function can be expanded about w. w x y z 0 0 0 1 1 0 1 a# 0 2 2 Column Sums : x y z 1 1 2 The column sums can be made by complementing the columns corresponding to variables x and y. Boolean Algebra 81

x’ 1 1 0 y’ 1 0 1 z 0 1 1 a# 2 2 2 Column Sums: x y z 2 2 2 Each row is tested by the binomial coefficients for sufficient occurrence. 3!/(3 -2)!2! = 3 Symmetry: S 2(x’, y’, z) Boolean Algebra 82

w x y z 1 0 1 1 0 0 1 1 2 2 1 x 0 1 1 2 y 1 0 1 2 z’ 1 1 0 2 a# 1 The column sums can be made 1 the same by complementing 3 the columns corresponding to variable z. a# 2 2 2 Each row is tested by the binomial coefficients for sufficient occurrence. Boolean Algebra 83

3!/(3 -2)! 2! = 3 Symmetry: S 2(x, y, z’) So the function f is written as f=w’S 2(x’, y’, z) + w. S 2(x, y, z’) Boolean Algebra 84

questions? Boolean Algebra 85