Laws Rules of Boolean Algebra Commutative law of

Laws & Rules of Boolean Algebra
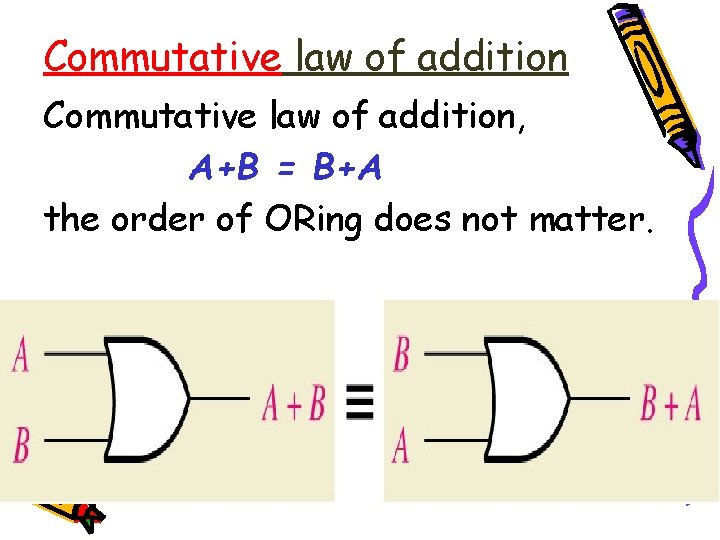
Commutative law of addition, A+B = B+A the order of ORing does not matter.

Commutative law of Multiplication AB = BA the order of ANDing does not matter.
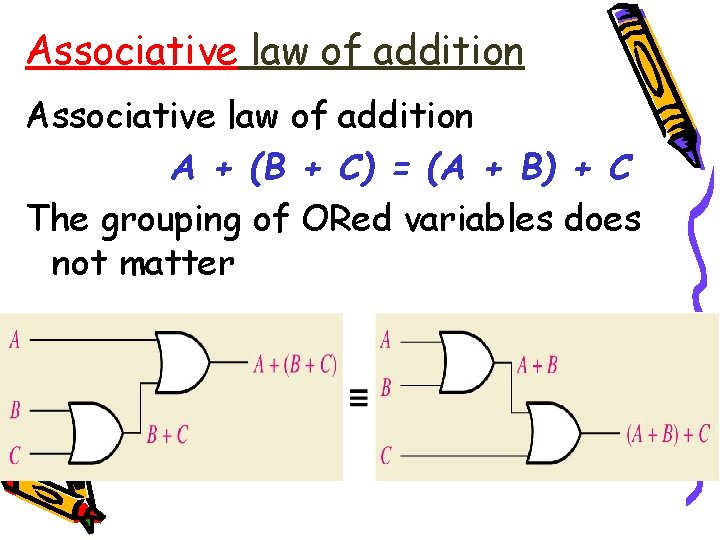
Associative law of addition A + (B + C) = (A + B) + C The grouping of ORed variables does not matter
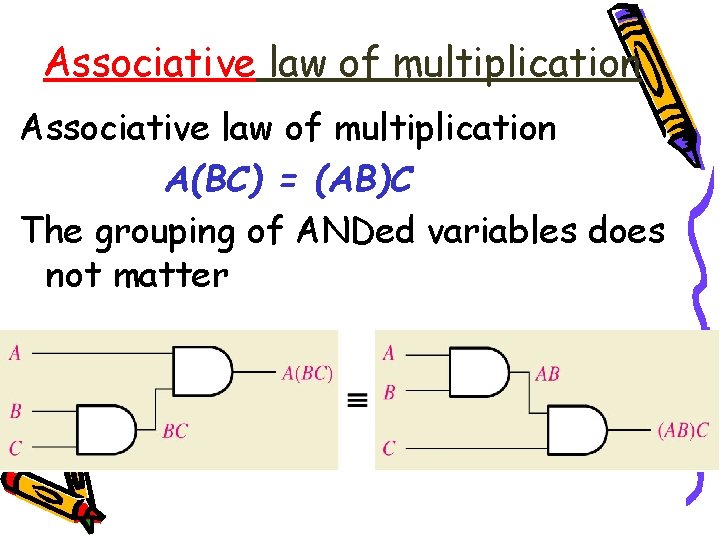
Associative law of multiplication A(BC) = (AB)C The grouping of ANDed variables does not matter
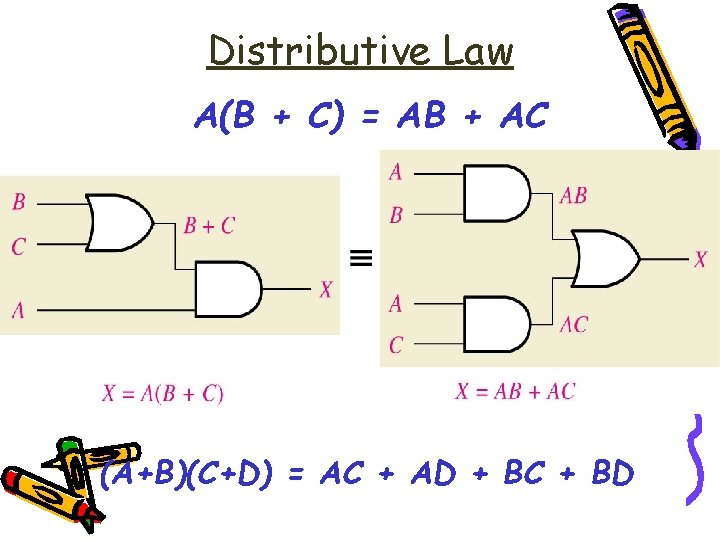
Distributive Law A(B + C) = AB + AC (A+B)(C+D) = AC + AD + BC + BD

Boolean Rules 1) A + 0 = A • In math if you add 0 you have changed nothing • In Boolean Algebra ORing with 0 changes nothing
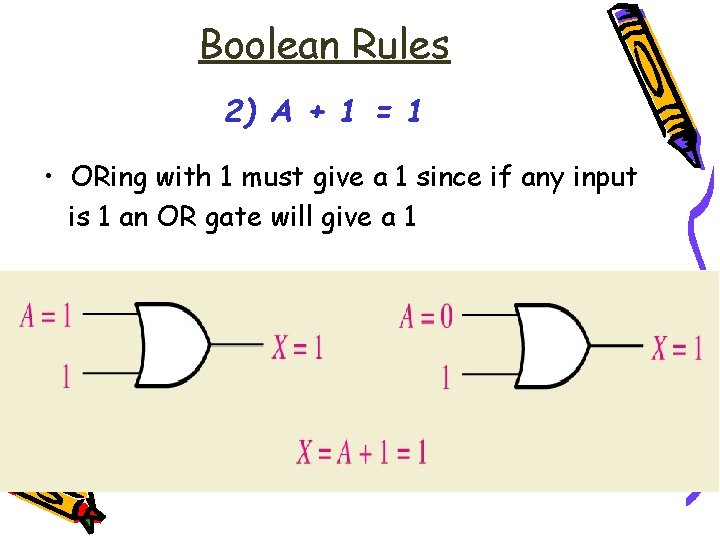
Boolean Rules 2) A + 1 = 1 • ORing with 1 must give a 1 since if any input is 1 an OR gate will give a 1

Boolean Rules 3) A • 0 = 0 • In math if 0 is multiplied with anything you get 0. If you AND anything with 0 you get 0

Boolean Rules 4) A • 1 = A • ANDing anything with 1 will yield the anything
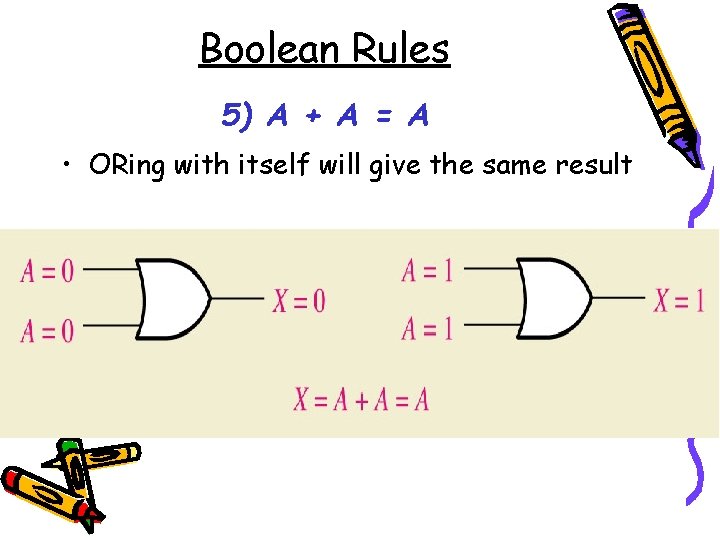
Boolean Rules 5) A + A = A • ORing with itself will give the same result
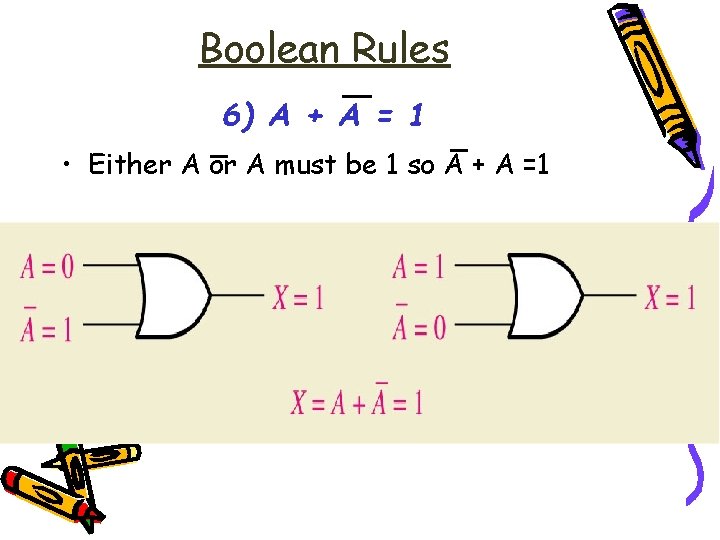
Boolean Rules 6) A + A = 1 • Either A or A must be 1 so A + A =1
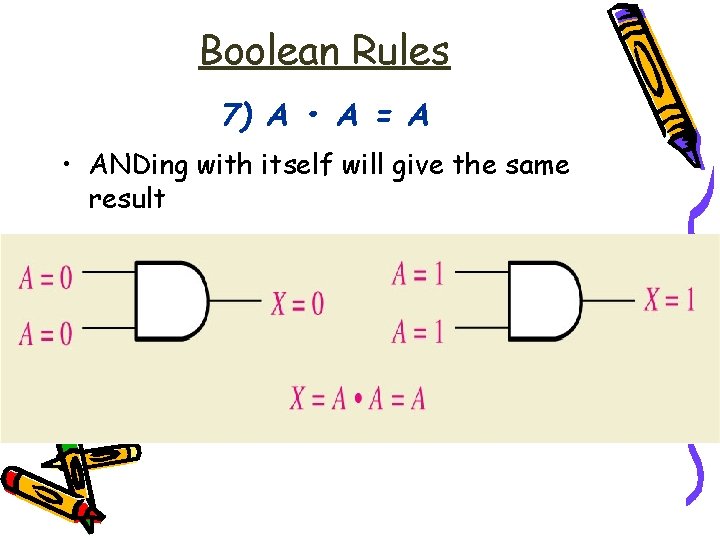
Boolean Rules 7) A • A = A • ANDing with itself will give the same result
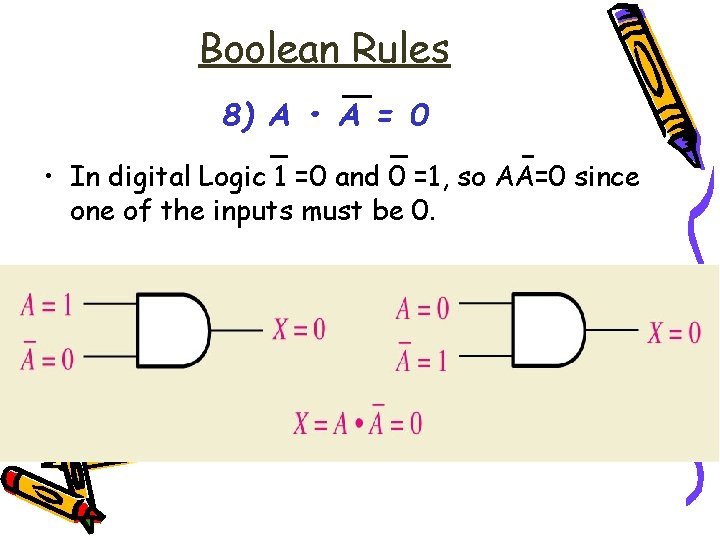
Boolean Rules 8) A • A = 0 • In digital Logic 1 =0 and 0 =1, so AA=0 since one of the inputs must be 0.

Boolean Rules 9) A = A • If you not something twice you are back to the beginning

Boolean Rules 10) A + AB = A Proof: A + AB = A(1 +B) DISTRIBUTIVE LAW = A∙ 1 RULE 2: (1+B)=1 =A RULE 4: A∙ 1 = A

Boolean Rules 11) A + AB = A + B • If A is 1 the output is 1 , If A is 0 the output is BProof: A + AB = (A + AB) + AB RULE 10 = (AA +AB) + AB RULE 7 = AA + AB + AA +AB RULE 8 = (A + A)(A + B) FACTORING = 1∙(A + B) RULE 6 =A+B RULE 4

Boolean Rules 12) (A + B)(A + C) = A + BC PROOF (A + B)(A +C) = AA + AC +AB +BC DISTRIBUTIVE LAW = A + AC + AB + BC RULE 7 = A(1 + C) +AB + BC FACTORING = A. 1 + AB + BC RULE 2 = A(1 + B) + BC FACTORING = A. 1 + BC RULE 2 = A + BC RULE 4

END OF BOOLEAN RULES & LAWS

De. Morgan’s Theorem ENT 116

Theorems The complement of two or more ANDed variables is equivalent to the OR of the complements of the individual variables The complement of two or more ORed variables is equivalent to the AND of the complements of the individual variables
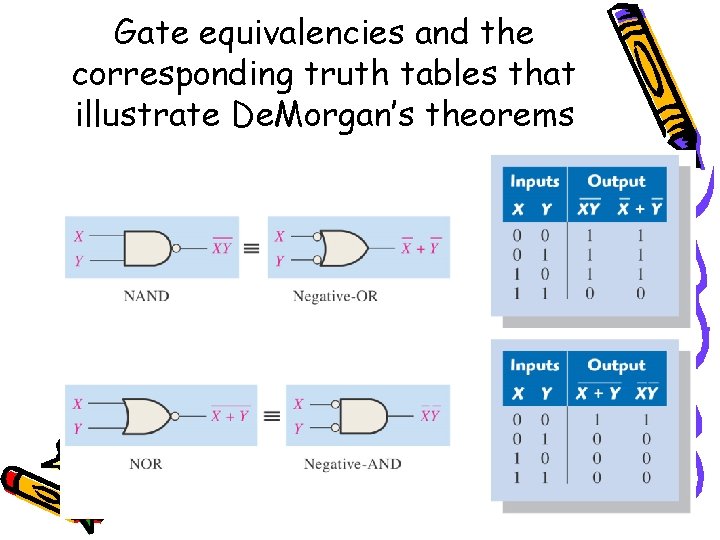
Gate equivalencies and the corresponding truth tables that illustrate De. Morgan’s theorems
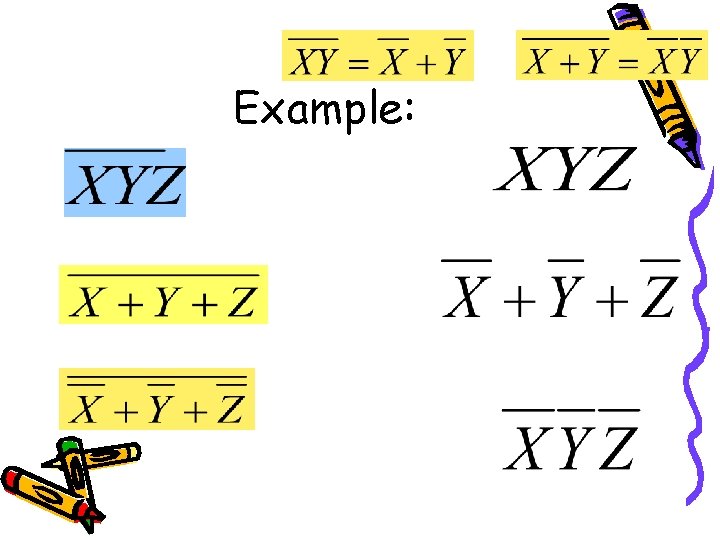
Example:
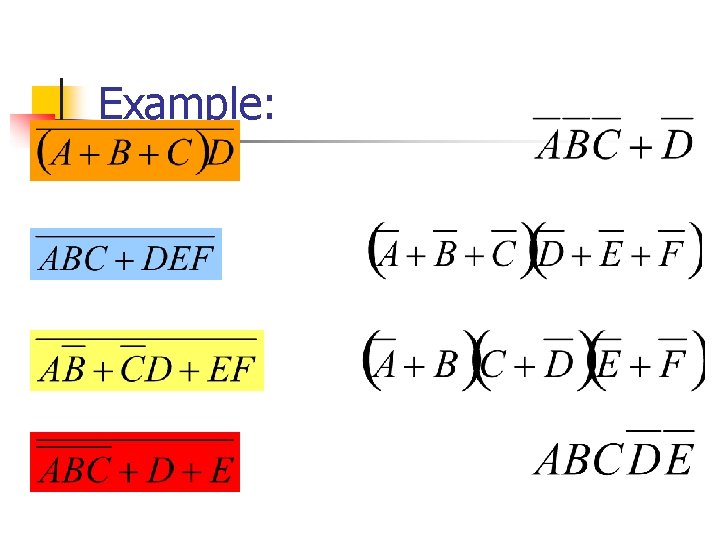
Example:
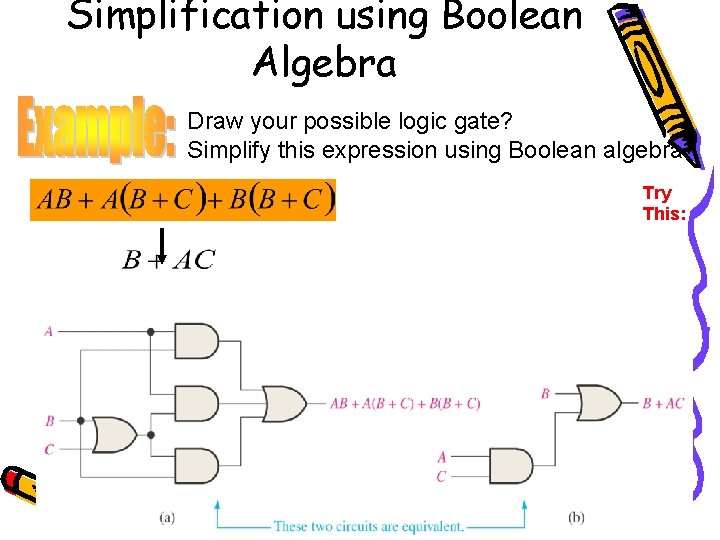
Simplification using Boolean Algebra Draw your possible logic gate? Simplify this expression using Boolean algebra? Try This:
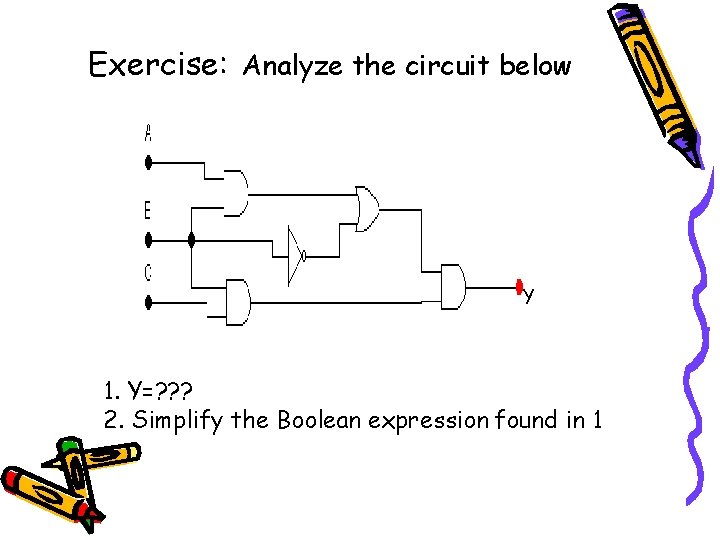
Exercise: Analyze the circuit below Y 1. Y=? ? ? 2. Simplify the Boolean expression found in 1
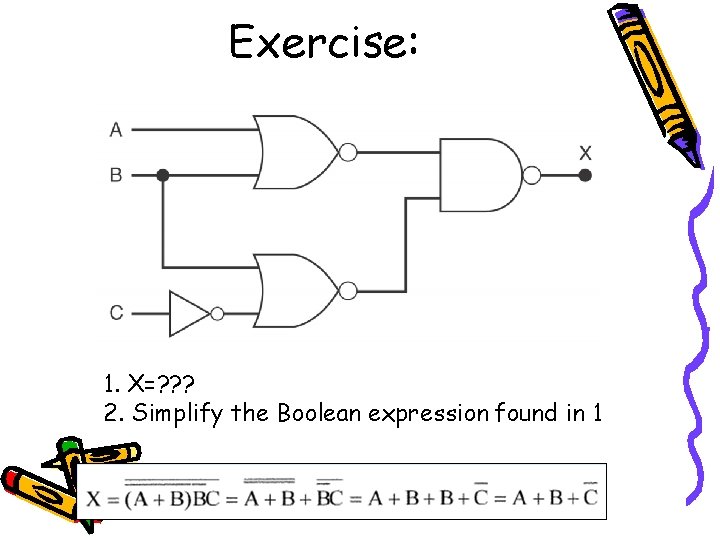
Exercise: 1. X=? ? ? 2. Simplify the Boolean expression found in 1
Karnaugh Map Standard Forms of Boolean Expressions Sum of Product (SOP) Product of Sum (POS)
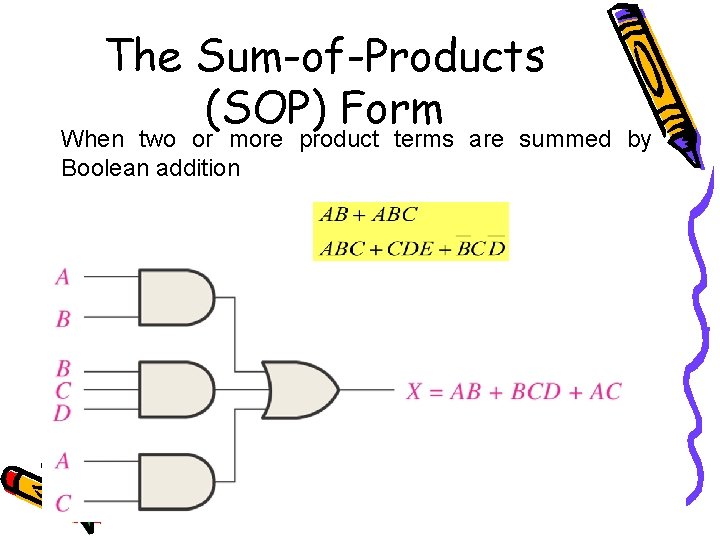
The Sum-of-Products (SOP) Form When two or more product terms are summed by Boolean addition

Conversion of a General Expression to SOP Form Any logic expression can be change into SOP form by applying Boolean Algebra techniques Try This:
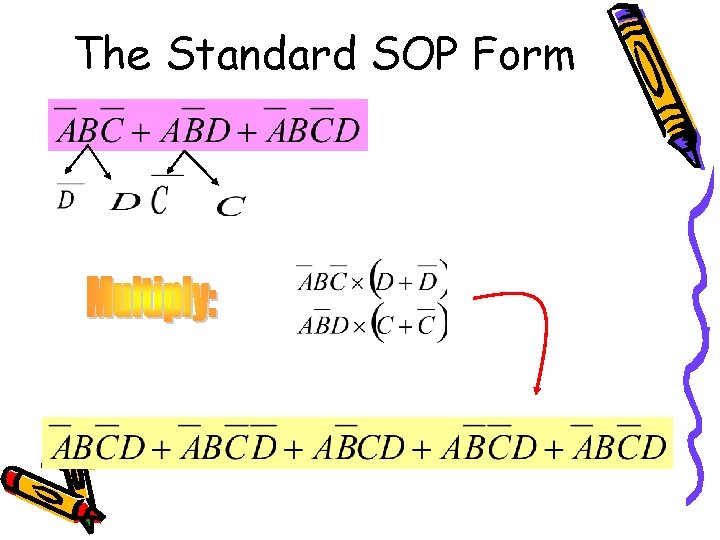
The Standard SOP Form
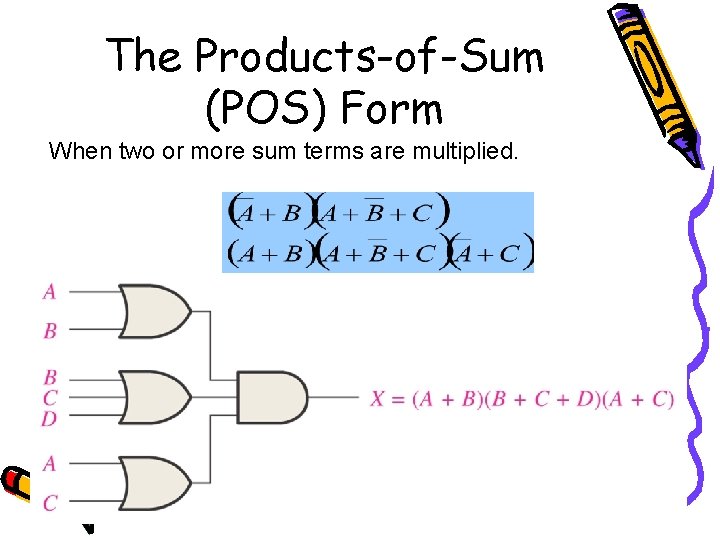
The Products-of-Sum (POS) Form When two or more sum terms are multiplied.
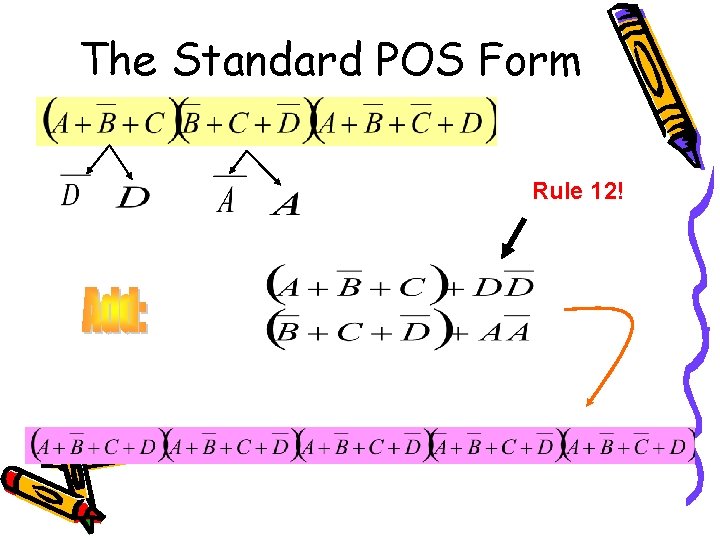
The Standard POS Form Rule 12!

Boolean Expression and Truth Table
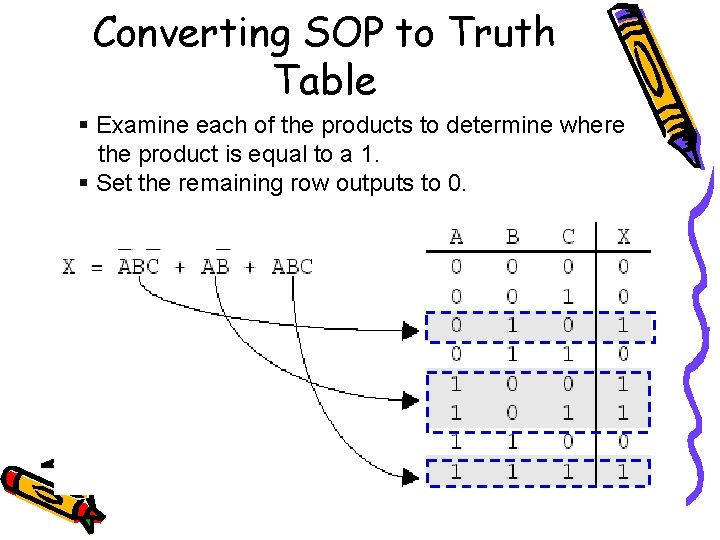
Converting SOP to Truth Table § Examine each of the products to determine where the product is equal to a 1. § Set the remaining row outputs to 0.
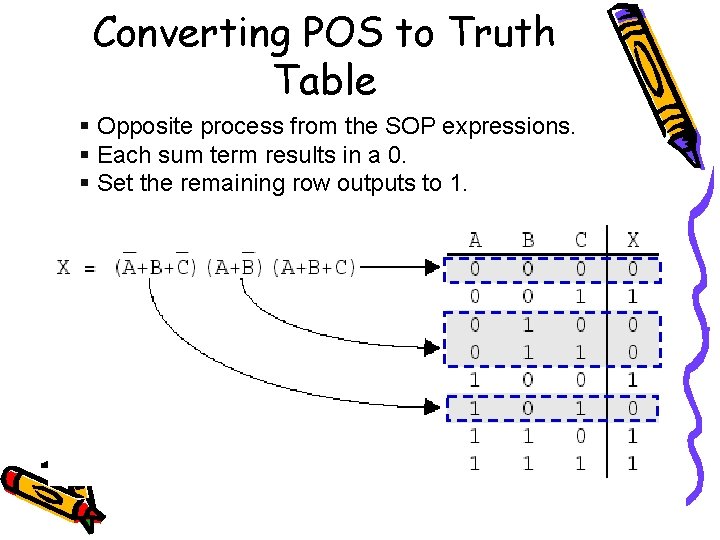
Converting POS to Truth Table § Opposite process from the SOP expressions. § Each sum term results in a 0. § Set the remaining row outputs to 1.
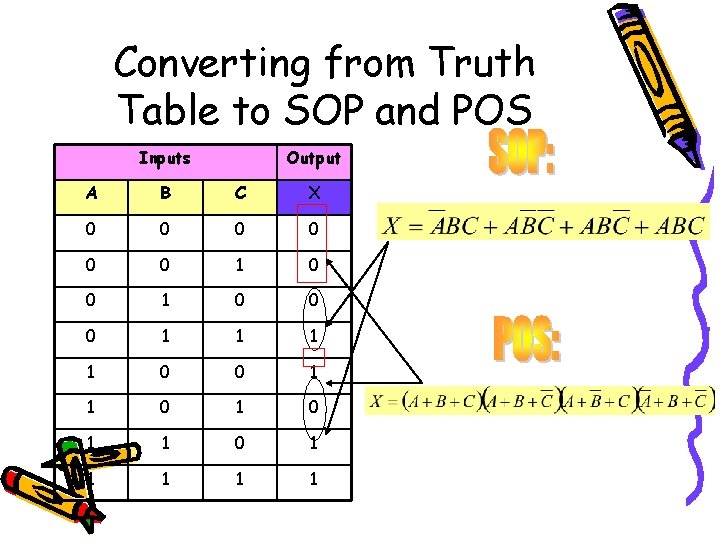
Converting from Truth Table to SOP and POS Inputs Output A B C X 0 0 0 1 1 0 0 1 1 1
The Karnaugh Map
The Karnaugh Map • Provides a systematic method for simplifying Boolean expressions • Produces the simplest SOP or POS expression • Similar to a truth table because it presents all of the possible values of input variables
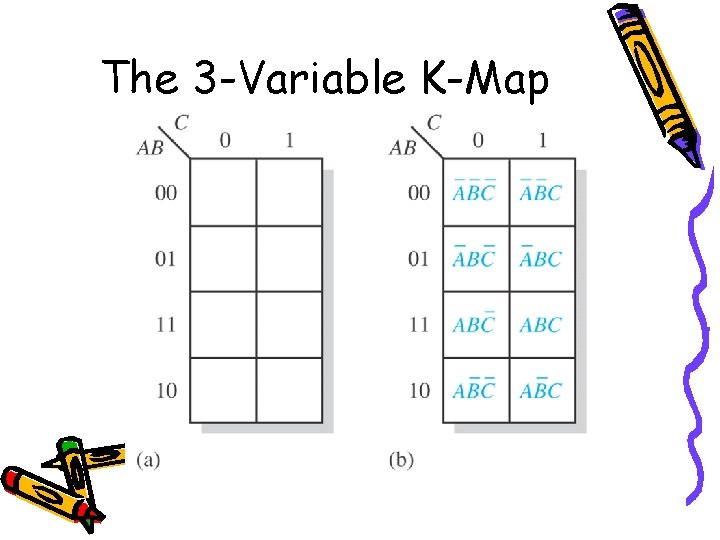
The 3 -Variable K-Map
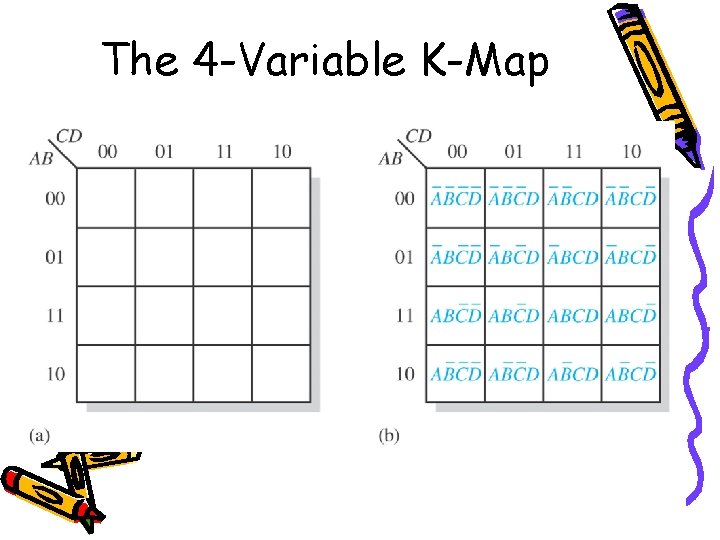
The 4 -Variable K-Map
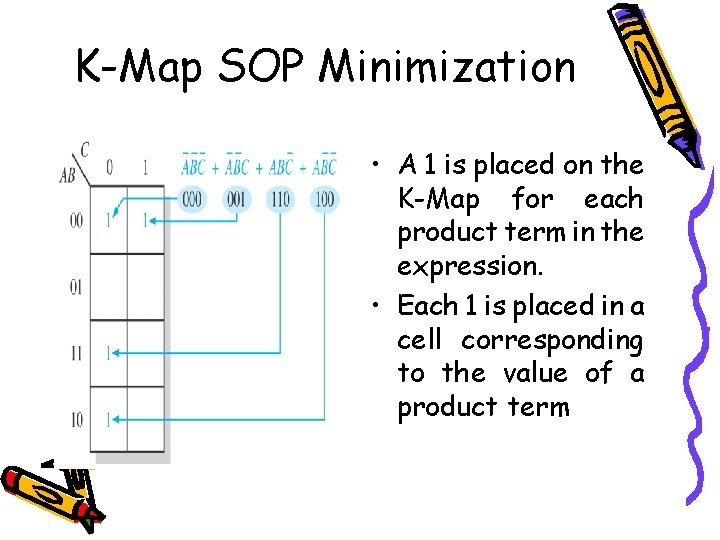
K-Map SOP Minimization • A 1 is placed on the K-Map for each product term in the expression. • Each 1 is placed in a cell corresponding to the value of a product term
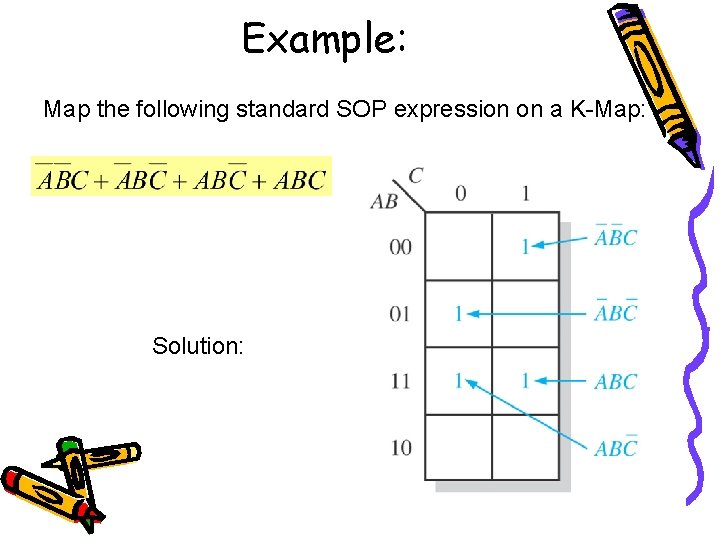
Example: Map the following standard SOP expression on a K-Map: Solution:
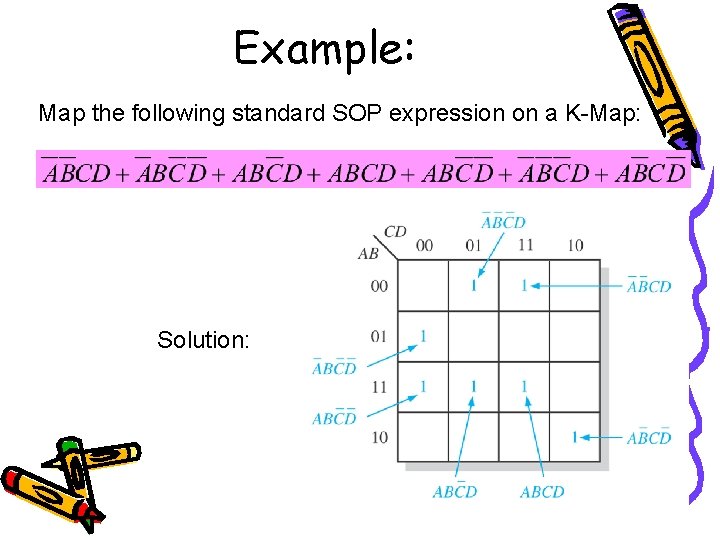
Example: Map the following standard SOP expression on a K-Map: Solution:

Exercise: Map the following standard SOP expression on a K-Map:
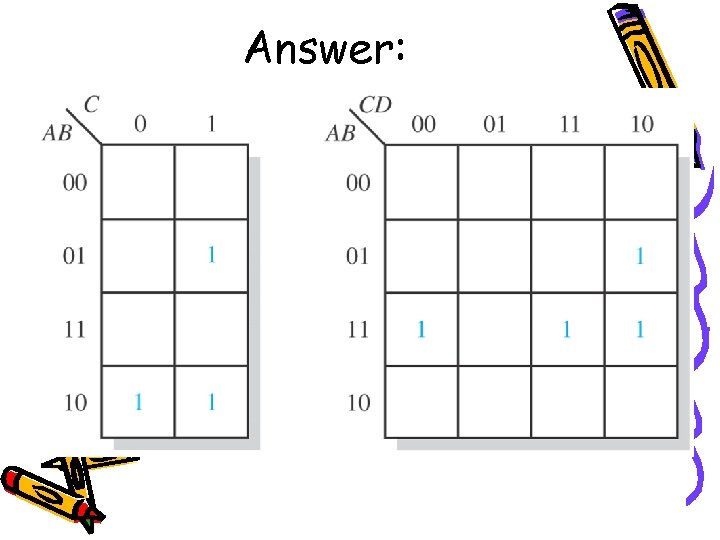
Answer:

K-Map Simplification of SOP Expressions • A group must contain either 1, 2, 4, 8 or 16 cells. • Each cell in group must be adjacent to one or more cells in that same group but all cells in the group do not have to be adjacent to each other • Always include the largest possible number 1 s in a group in accordance with rule 1 • Each 1 on the map must be included in at least one group. The 1 s already in a group can be included in another group as long as the overlapping groups include noncommon 1 s To maximize the size of the groups and to minimize the number of groups
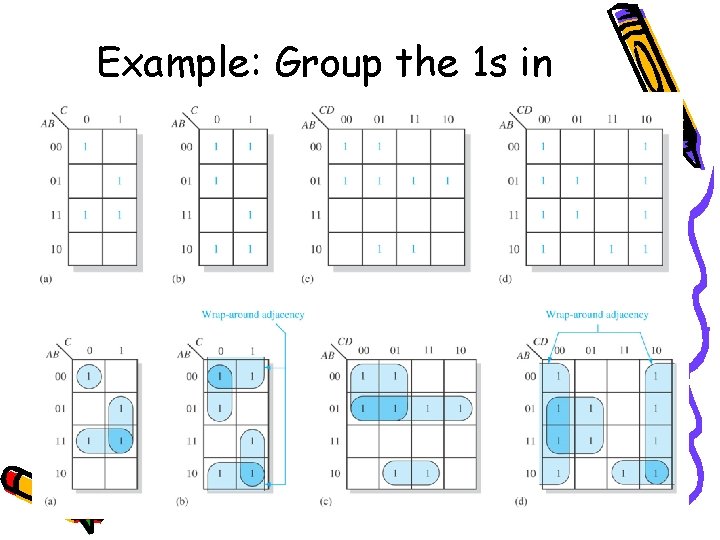
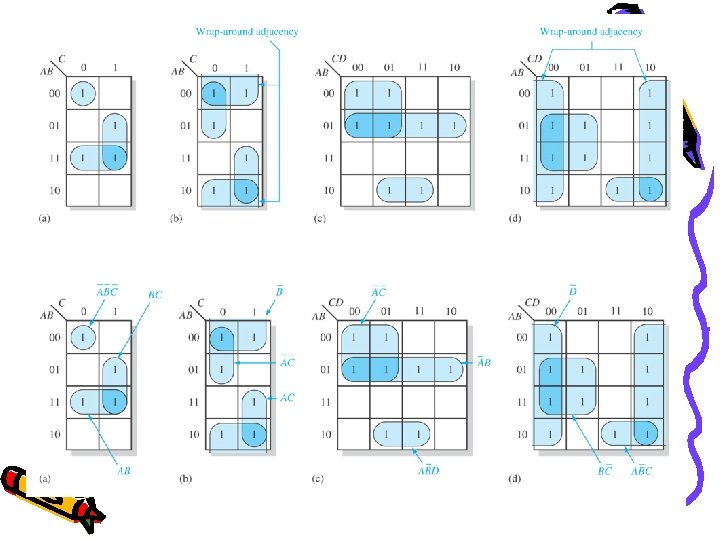
Example: Group the 1 s in each K-Maps

Determining the minimum SOP Expression from the Map • Groups the cells that have 1 s. • Each group of cells containing 1 s create one product term composed of all variables that occur in only one form (either uncomplemented or complemented) within the group. • Variable that occurs both uncomplemented and complemented within the group are eliminated. These are called contradictory variables.
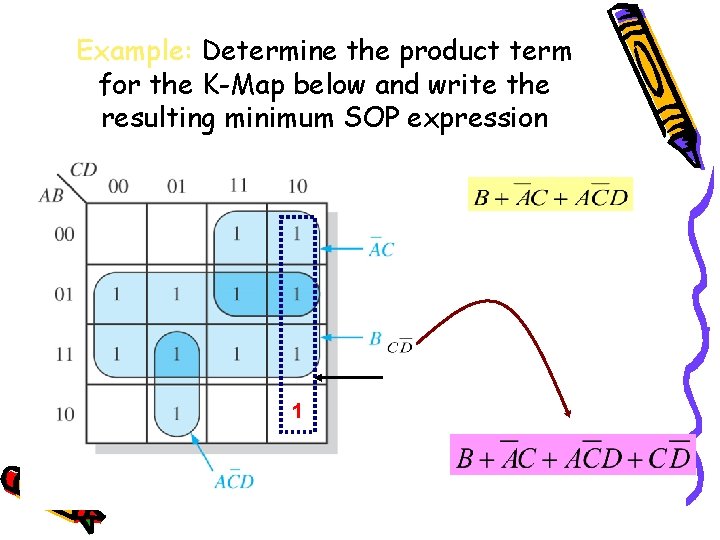
Example: Determine the product term for the K-Map below and write the resulting minimum SOP expression 1
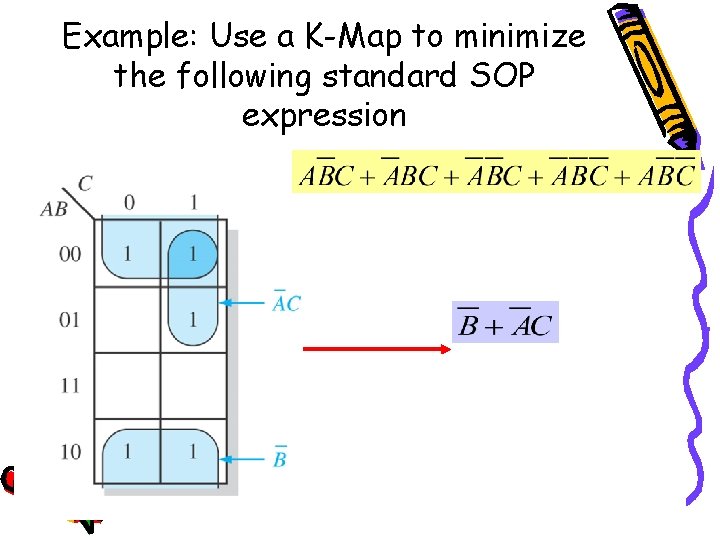
Example: Use a K-Map to minimize the following standard SOP expression
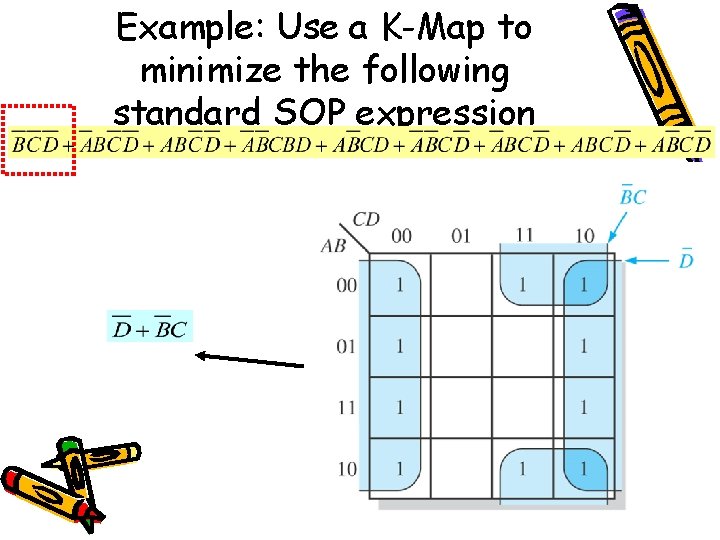
Example: Use a K-Map to minimize the following standard SOP expression
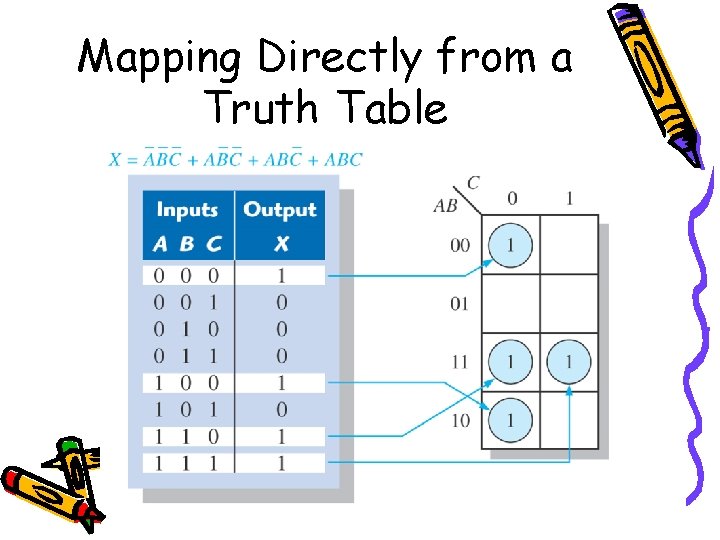
Mapping Directly from a Truth Table

Don’t Care (X) Conditions • A situation arises in which input variable combinations are not allowed • Don’t care terms either a 1 or a 0 may be assigned to the output

Don’t Care (X) Conditions Example of the use of “don’t care” conditions to simplify an expression
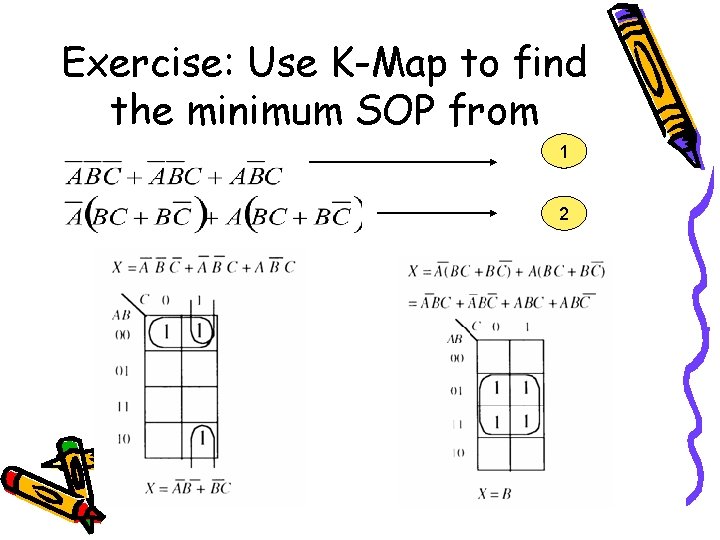
Exercise: Use K-Map to find the minimum SOP from 1 2

Exercise a) Construct the truth table for the above function b) Simplify the expression using Boolean algebra and/or De-Morgan c) Simplify using K-Map d) Draw circuits for both (b) and (c)

Exercise Design a logic circuit having 3 inputs, A, B, C will have its output HIGH only when a majority of the inputs are HIGH. a) Construct the truth table b) Simplify the expression using Boolean algebra and/or De-Morgan c) Simplify using K-Map d) Draw circuits for both (b) and (c)
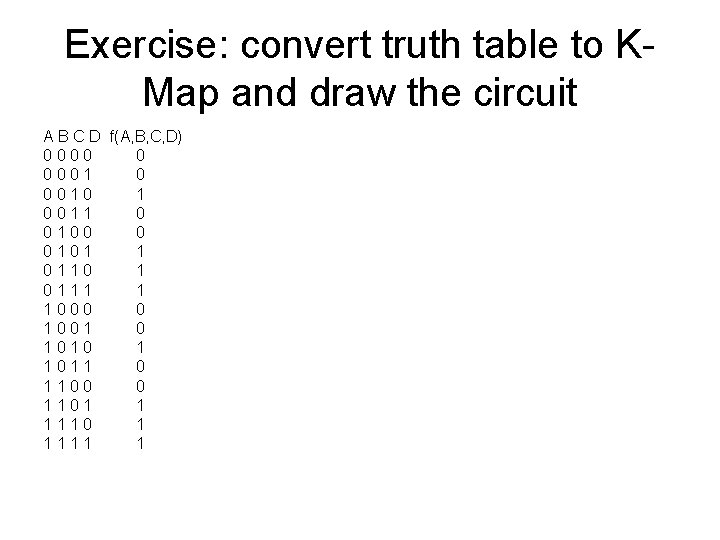
Exercise: convert truth table to KMap and draw the circuit A B C D f(A, B, C, D) 0000 0 0001 0 0010 1 0011 0 0100 0 0101 1 0110 1 0111 1 1000 0 1001 0 1010 1 1011 0 1100 0 1101 1 1110 1 1111 1

Exercise • Design a 3 -variables Gray to Binary converter and build the simplified circuit. • Try at home: Design a 3 -variables Binary to Gray converter and build the simplified circuit.

Binary – to – Gray Code Conversion Rules : • The most significant bit (left – most) in the Gray code is the same as the corresponding MSB in the binary number. • Going from left to right, add each adjacent pair of binary code bits to get the next Gray code bit. Discard carries. • Example : 10110 to gray code. (11101)

Gray – to – Binary Conversion Rules : • The most significant bit (left – most) in the binary code is the same as the corresponding bit in the Gray code. • Add each binary code bit generated to the Gray code bit in the next adjacent position. Discard carries. • Example : gray code word 11011 to binary

Decimal BCD Binary coded decimal (BCD) is a weighted code that is commonly used in digital systems when it is necessary to show decimal numbers such as in clock displays. The table illustrates the difference between straight binary and BCD represents each decimal digit with a 4 -bit code. Notice that the codes 1010 through 1111 are not used in BCD. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Binary 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 BCD 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001

Exercise • Reduce the following equation using both Boolean algebra and Karnaugh Maps to a circuit with the fewest number of gates.
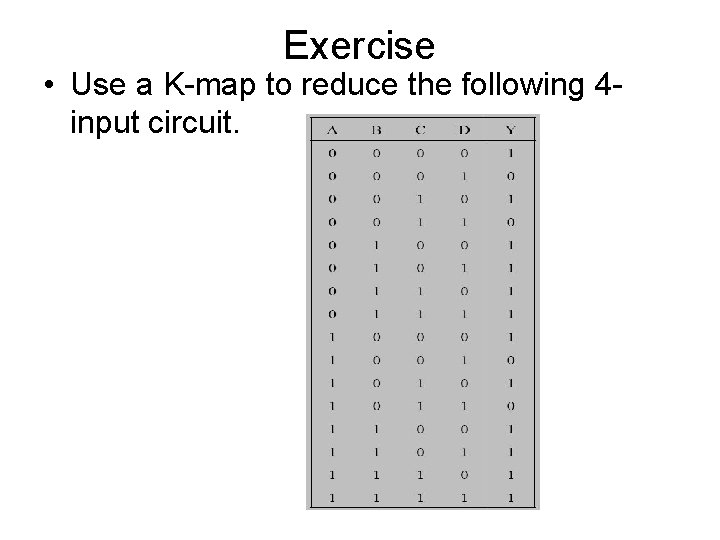
Exercise • Use a K-map to reduce the following 4 input circuit.

1. The associative law for addition is normally written as a. A + B = B + A b. (A + B) + C = A + (B + C) c. AB = BA d. A + AB = A © 2008 Pearson Education

2. The Boolean equation AB + AC = A(B+ C) illustrates a. the distribution law b. the commutative law c. the associative law d. De. Morgan’s theorem © 2008 Pearson Education

3. The Boolean expression A. 1 is equal to a. A b. B c. 0 d. 1 © 2008 Pearson Education

4. The Boolean expression A + 1 is equal to a. A b. B c. 0 d. 1 © 2008 Pearson Education

5. The Boolean equation AB + AC = A(B+ C) illustrates a. the distribution law b. the commutative law c. the associative law d. De. Morgan’s theorem © 2008 Pearson Education

6. A Boolean expression that is in standard SOP form is a. the minimum logic expression b. contains only one product term c. has every variable in the domain in every term d. none of the above © 2008 Pearson Education

7. Adjacent cells on a Karnaugh map differ from each other by a. one variable b. two variables c. three variables d. answer depends on the size of the map © 2008 Pearson Education
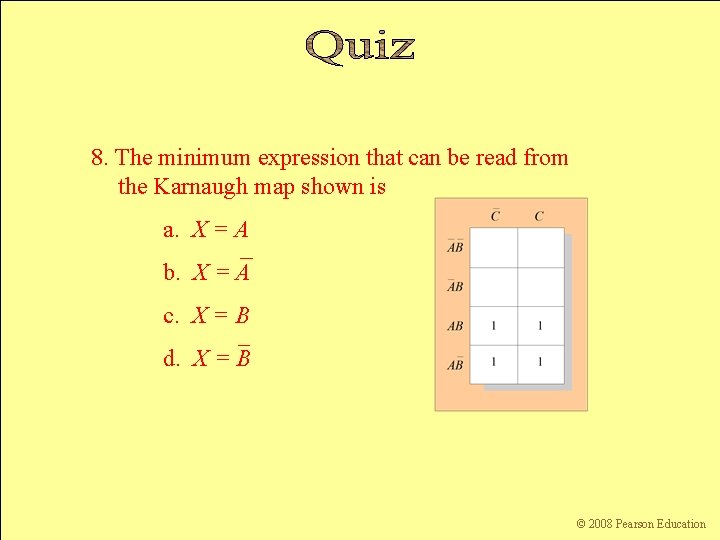
8. The minimum expression that can be read from the Karnaugh map shown is a. X = A b. X = A c. X = B d. X = B © 2008 Pearson Education
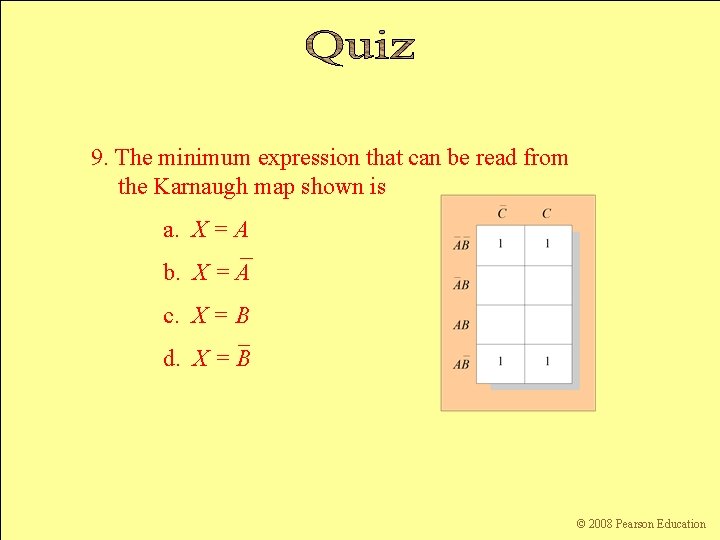
9. The minimum expression that can be read from the Karnaugh map shown is a. X = A b. X = A c. X = B d. X = B © 2008 Pearson Education
- Slides: 75