Boolean Algebra Gates and Digital Logic BOOLEAN ALGEBRA

Boolean Algebra, Gates and Digital Logic

BOOLEAN ALGEBRA • Boolean algebra is an algebra for the manipulation of objects that can take on only two values, typically true and false, although it can be any pair of values. • Computers are built as collections of switches that are either “on” or “off, ” Boolean algebra is a very natural way to represent digital information. • Digital circuits in digital electronics use low and high voltages, but for our level of understanding, 0 and 1 will suffice. • Boolean algebra is an algebraic structure defined on a set of elements B, together with two binary operators(+, . )

Boolean Expressions • Boolean Algebra has operations we can be performed on binary objects or variables. When we combine the variables and operators form a Boolean expression • In Boolean algebra, all the variables have the values 0 or 1 and, in typical formulations, there are three operators • Three most common Boolean operators: AND, OR, NOT

Boolean Expressions • The OR operator is written as , as in x+y. The result of an OR operator is 1 if either of the variables is 1. The OR operation is also called a logical sum, since its result is 1 if either operand is 1. • The AND operator is written as , as in xy. The result of an AND operator is 1 only if both inputs are 1. Th e AND operator is also called logical product, since its result is 1 only if both operands are 1. • The unary operator NOT is written as x’. Th e result of a NOT operator is 1 only if the input is 0. Applying the operator NOT to a logical value results in an inversion or negation of the value (i. e. , if the input is 0 the output is 1, and vice versa).

Boolean Identities • There are several laws of Boolean algebra that are helpful in manipulating logic equations

Boolean Identities • De Morgan's Theorem 1. (A + B)’ = A’B’ 2. (AB)’ = A’ + B’

Truth Table for AND Inputs Outputs x y xy 0 0 0 0 1 0 1 0 0 1 1 1 The logical operator AND is typically represented by either a dot or no symbol at all. For example, the Boolean expression xy is equivalent to the expression x · y and is read “x and y. ” The expression xy is often referred to as a Boolean product. The result of the expression xy is 1 only when both inputs are 1, and 0 otherwise.

Truth Table for OR Inputs Outputs x y x + y 0 0 0 0 1 1 1 0 1 1
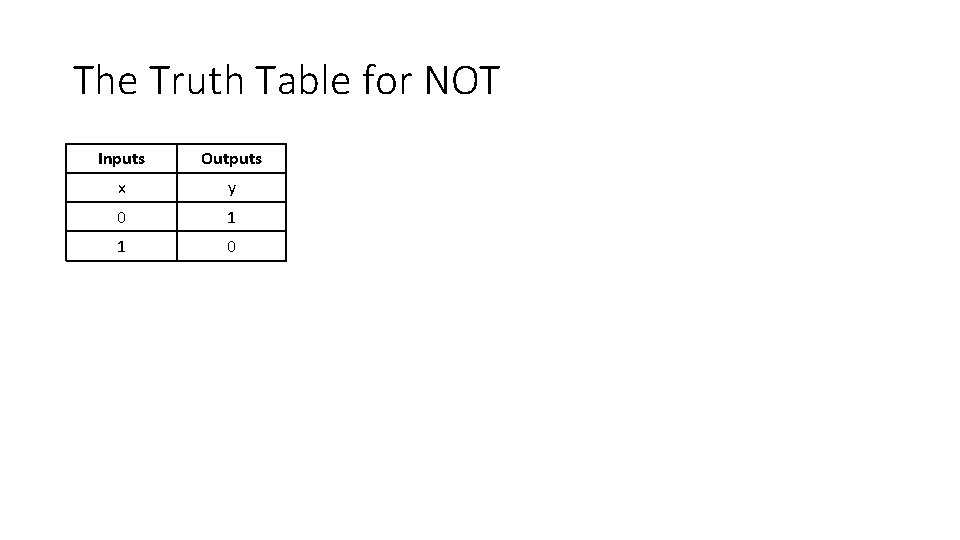
The Truth Table for NOT Inputs Outputs x y 0 1 1 0

Gates and Digital Logic Circuits • The electronics inside a modern computer are digital. • Digital electronics operate with only two voltage levels of interest: a high voltage and a low voltage. All other voltage values are temporary and occur while transitioning between the values. • The fact that computers are digital is also a key reason they use binary numbers, since a binary system matches the underlying abstraction inherent in the electronics. • Rather than refer to the voltage levels, we talk about signals that are (logically) true, or 1, or are asserted; or signals that are (logically) false, or 0, or are deasserted. • The values 0 and 1 are called complements or inverses of one another.

Digital Logic Circuits • Electronic circuits that handle information encoded in binary form (deal with signals that have only two values, 0 and 1)

Gates Continued… • Asserted signal: A signal that is (logically) true, or 1. • Deasserted signal: A signal that is (logically) false, or 0. • Logic blocks are categorized as one of two types 1. Combinational logic: A logic system whose blocks do not contain memory and hence compute the same output given the same input. 2. Sequential logic: A group of logic elements that contain memory and hence whose value depends on the input as well as the current contents of the memory.

Gates Continued • A gate is a device that implements basic logic functions, such as AND or OR. • An AND gate implements the AND function, and an OR gate implements the OR function. • Both AND and OR are commutative and associative, an AND or an OR gate can have multiple inputs, with the output equal to the AND or OR of all the inputs. • Th e logical function NOT is implemented with an inverter that always has a single input. • To draw a NOT, the common practice is to add “bubbles” to the inputs or outputs of a gate to cause the logic value on that input line or output line to be inverted.
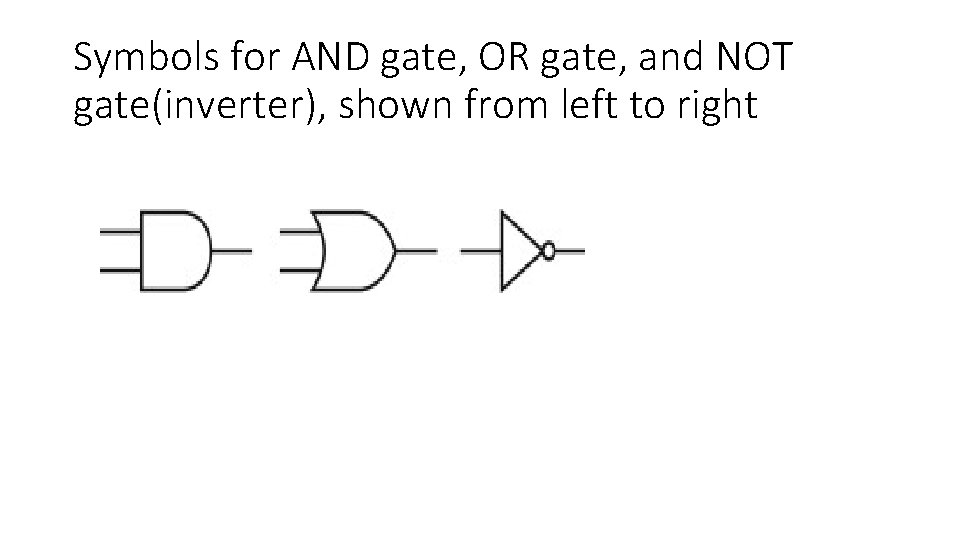
Symbols for AND gate, OR gate, and NOT gate(inverter), shown from left to right

Three categories of gates • Basic gates: The basic gates are AND, OR & NOT gates. • Universal gates: NAND & NOR gates are called as universal gates. • Special gates: Ex-OR & Ex-NOR gates are called as special gates
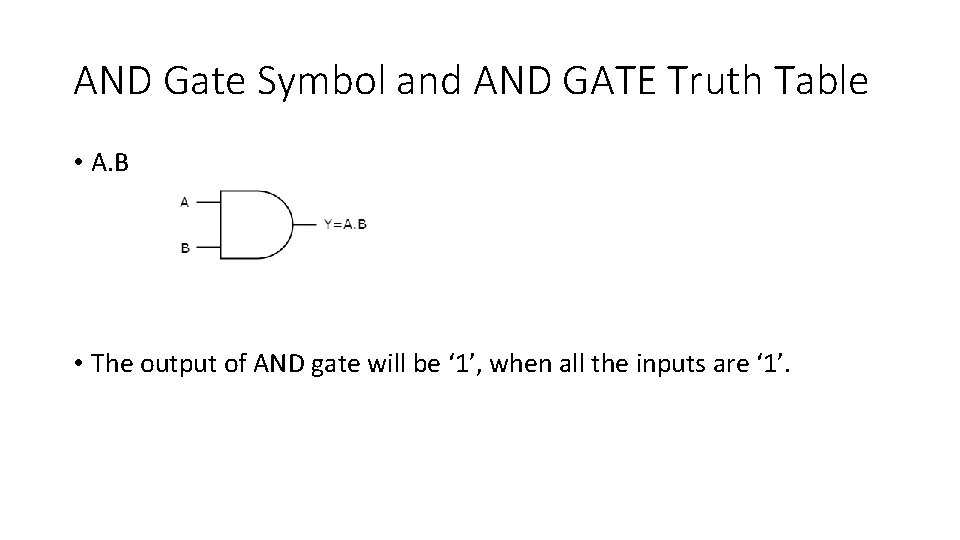
AND Gate Symbol and AND GATE Truth Table • A. B • The output of AND gate will be ‘ 1’, when all the inputs are ‘ 1’.

OR Gate • A + B • The output of an OR gate will be ‘ 1’, when at least one of those inputs is ‘ 1’.

NOT Gate • A NOT gate is a digital circuit that has single input and single output. The output of NOT gate is the logical inversion of input. Hence, the NOT gate is also called as inverter. • This NOT gate produces an output YY, which is the complement of input, A.

Universal gates • NAND & NOR gates are called as universal gates. Because we can implement any Boolean function, which is in sum of products form by using NAND gates alone. We can also implement a Boolean function that is a product of sums form using NOR gate alone. • Any logical function can be constructed using AND gates, OR gates, and inversion • NOR gate: An inverted OR gate. • NAND gate: An inverted AND gate.
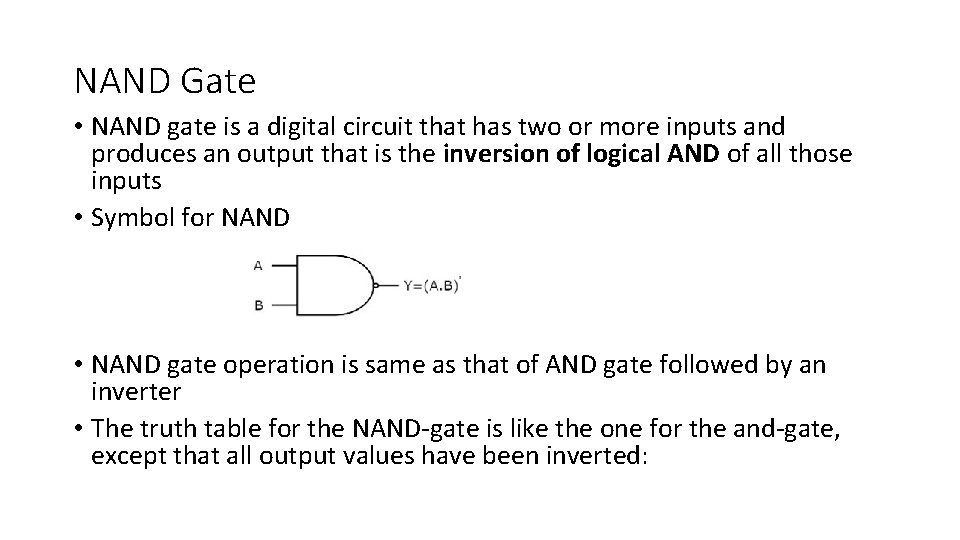
NAND Gate • NAND gate is a digital circuit that has two or more inputs and produces an output that is the inversion of logical AND of all those inputs • Symbol for NAND • NAND gate operation is same as that of AND gate followed by an inverter • The truth table for the NAND-gate is like the one for the and-gate, except that all output values have been inverted:

NOR gate • NOR gate is a digital circuit that has two or more inputs and produces an output that is the inversion of logical OR of all those inputs. • Symbol of NOR gate • The truth table for the nor-gate is like the one for the or-gate, except that all output values have been inverted:
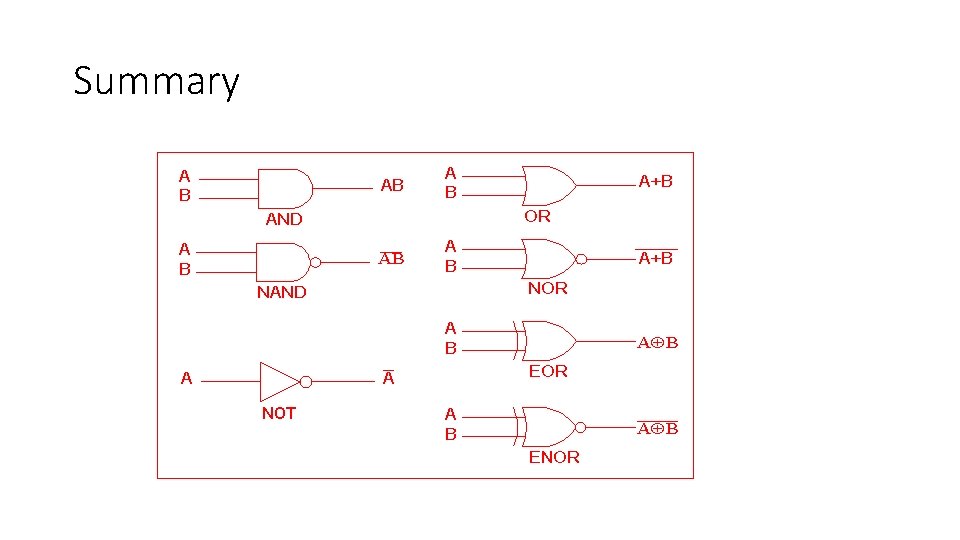
Summary

Three Input AND Gate A B C A. B. C 0 0 0 1 1 0 0 0 1 0 1 1 1 1 1
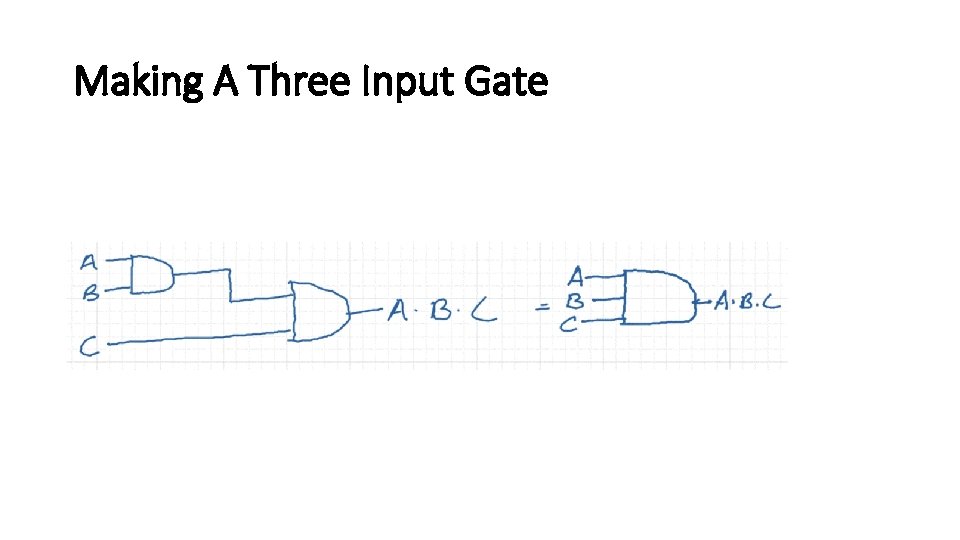
Making A Three Input Gate

In class Activity- Four Input AND Gate • Create a multiple input AND gate by drawing four input AND gate and its truth table

In-class Activity • Create a multiple input OR gates by drawing three and four input OR gates and their truth tables

Gates and Integrated Circuits • Gates are not sold individually • They are sold in units called integrated circuits (ICs). • A chip is a small electronic device consisting of the necessary electronic components (transistors, resistors, and capacitors) to implement various gates.

Reading • Hennessy and Patterson Chapter 8. 2 (Appendix B)
- Slides: 28