Combinational logic z Logic functions truth tables and

Combinational logic z Logic functions, truth tables, and switches y NOT, AND, OR, NAND, NOR, XOR, . . . y Minimal set z Axioms and theorems of Boolean algebra y Proofs by re-writing y Proofs by perfect induction z Gate logic y Networks of Boolean functions y Time behavior z Canonical forms y Two-level y Incompletely specified functions z Simplification y Boolean cubes and Karnaugh maps y Two-level simplification CS 150 - Fall 2000 - Combinational Logic - 1

Possible logic functions of two variables z There are 16 possible functions of 2 input variables: y in general, there are 2**(2**n) functions of n inputs X Y X 0 0 1 1 Y 0 1 0 0 0 X and Y 0 0 0 1 0 X 0 0 1 1 0 0 Y F 16 0 1 possible functions (F 0–F 15) 0 0 1 1 1 0 0 1 1 0 1 0 1 X xor Y X=Y X nor Y not (X or Y) CS 150 - Fall 2000 - Combinational Logic - 2 not Y 1 1 0 0 1 1 1 1 0 1 1 1 X nand Y not (X and Y) not X

Cost of different logic functions z Different functions are easier or harder to implement y Each has a cost associated with the number of switches needed y 0 (F 0) and 1 (F 15): require 0 switches, directly connect output to low/high y X (F 3) and Y (F 5): require 0 switches, output is one of inputs y X' (F 12) and Y' (F 10): require 2 switches for "inverter" or NOT-gate y X nor Y (F 4) and X nand Y (F 14): require 4 switches y X or Y (F 7) and X and Y (F 1): require 6 switches y X = Y (F 9) and X Y (F 6): require 16 switches y Because NOT, NOR, and NAND are the cheapest they are the functions we implement the most in practice CS 150 - Fall 2000 - Combinational Logic - 3

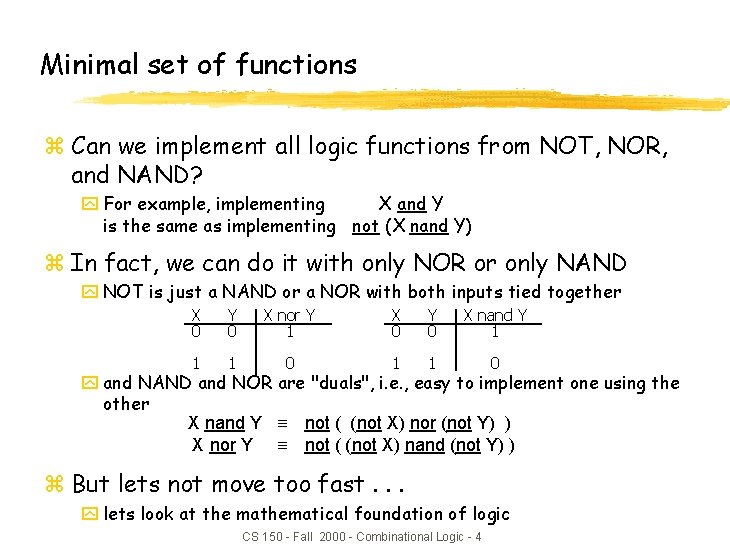
Minimal set of functions z Can we implement all logic functions from NOT, NOR, and NAND? y For example, implementing X and Y is the same as implementing not (X nand Y) z In fact, we can do it with only NOR or only NAND y NOT is just a NAND or a NOR with both inputs tied together X 0 Y 0 X nor Y 1 X 0 Y 0 X nand Y 1 1 1 0 y and NAND and NOR are "duals", i. e. , easy to implement one using the other X nand Y not ( (not X) nor (not Y) ) X nor Y not ( (not X) nand (not Y) ) z But lets not move too fast. . . y lets look at the mathematical foundation of logic CS 150 - Fall 2000 - Combinational Logic - 4

An algebraic structure z An algebraic structure consists of y a set of elements B y binary operations { + , • } y and a unary operation { ' } y such that the following axioms hold: 1. set B contains at least two elements, a, b, such that a b 2. closure: a + b is in B a • b is in B 3. commutativity: a + b = b + a a • b = b • a 4. associativity: a + (b + c) = (a + b) + c a • (b • c) = (a • b) • c 5. identity: a+0=a a • 1=a 6. distributivity: a + (b • c) = (a + b) • (a + c) a • (b + c) = (a • b) + (a • c) 7. complementarity: a + a' = 1 a • a' = 0 CS 150 - Fall 2000 - Combinational Logic - 5

Boolean algebra z Boolean algebra y B = {0, 1} y + is logical OR, • is logical AND y ' is logical NOT z All algebraic axioms hold CS 150 - Fall 2000 - Combinational Logic - 6

Logic functions and Boolean algebra z Any logic function that can be expressed as a truth table can be written as an expression in Boolean algebra using the operators: ', +, and • X 0 0 1 1 Y 0 1 X • Y 0 0 0 1 X 0 0 1 1 Y 0 1 X' 1 1 0 0 X 0 0 1 1 Y' 1 0 X • Y 0 0 0 1 X, Y are Boolean algebra variables Y 0 1 X' • Y' 1 0 0 0 X' 1 1 0 0 X' • Y 0 1 0 0 ( X • Y ) + ( X' • Y' ) 1 0 ( X • Y ) + ( X' • Y' ) 0 1 � X = Y Boolean expression that is true when the variables X and Y have the same value and false, otherwise CS 150 - Fall 2000 - Combinational Logic - 7

Axioms and theorems of Boolean algebra z Identity z Null 1. X + 0 = X 1 D. X • 1 = X 2. X + 1 = 1 2 D. X • 0 = 0 z Idempotency: 3. X + X = X 3 D. X • X = X z Involution: 4. (X')' = X z Complementarity: 5. X + X' = 1 z Commutativity: 5 D. X • X' = 0 6. X + Y = Y + X z Associativity: 6 D. X • Y = Y • X 7. (X + Y) + Z = X + (Y + Z) 7 D. (X • Y) • Z = X • (Y • Z) CS 150 - Fall 2000 - Combinational Logic - 8

Axioms and theorems of Boolean algebra (cont’d) z Distributivity: 8. X • (Y + Z) = (X • Y) + (X • Z) (X + Z) z Uniting: 9. X • Y + X • Y' = X 8 D. X + (Y • Z) = (X + Y) • 9 D. (X + Y) • (X + Y') = X z Absorption: 10. X + X • Y = X 10 D. X • (X + Y) = X 11. (X + Y') • Y = X • Y 11 D. (X • Y') + Y = X + Y z Factoring: 12. (X + Y) • (X' + Z) = 12 D. X • Y + X' • Z = X • Z + X' • Y (X + Z) • (X' + Y) z Concensus: 13. (X • Y) + (Y • Z) + (X' • Z) = 17 D. (X + Y) • (Y + Z) • (X' + Z) = X • Y + X' • Z (X + Y) • (X' + Z) CS 150 - Fall 2000 - Combinational Logic - 9

Axioms and theorems of Boolean algebra (cont’) z de Morgan's: 14. (X + Y +. . . )' = X' • Y' • . . . 14 D. (X • Y • . . . )' = X' + Y' +. . . z generalized de Morgan's: 15. f'(X 1, X 2, . . . , Xn, 0, 1, +, • ) = f(X 1', X 2', . . . , Xn', 1, 0, • , +) z establishes relationship between • and + CS 150 - Fall 2000 - Combinational Logic - 10

Axioms and theorems of Boolean algebra (cont’) z Duality y Dual of a Boolean expression is derived by replacing • by +, + by • , 0 by 1, and 1 by 0, and leaving variables unchanged y Any theorem that can be proven is thus also proven for its dual! y Meta-theorem (a theorem about theorems) z duality: 16. X + Y +. . . X • Y • . . . z generalized duality: 17. f (X 1, X 2, . . . , Xn, 0, 1, +, • ) f(X 1, X 2, . . . , Xn, 1, 0, • , +) z Different than de. Morgan’s Law y this is a statement about theorems y this is not a way to manipulate (re-write) expressions CS 150 - Fall 2000 - Combinational Logic - 11

Proving theorems (rewriting) z Using the axioms of Boolean algebra: y e. g. , prove theorem: distributivity (8) complementarity (5) identity (1 D) y e. g. , prove theorem: identity (1 D) distributivity (8) identity (2) identity (1 D) X • Y + X • Y' = X X • Y + X • Y' X • (Y + Y') X • (1) X+X • Y = X • (Y + Y') = X • (1) = Xü = X X + X • Y X • 1 + X • Y X • (1 + Y) X • (1) CS 150 - Fall 2000 - Combinational Logic - 12 = = X • 1 + X • Y X • (1 + Y) X • (1) Xü

Proving theorems (perfect induction) z Using perfect induction (complete truth table): y e. g. , de Morgan's: (X + Y)' = X' • Y' NOR is equivalent to AND with inputs complemented X 0 0 1 1 Y 0 1 X' 1 1 0 0 Y' 1 0 (X + Y)' X' • Y' 1 1 0 0 0 (X • Y)' = X' + Y' NAND is equivalent to OR with inputs complemented X 0 0 1 1 Y 0 1 X' 1 1 0 0 Y' 1 0 (X • Y)' 1 1 1 0 CS 150 - Fall 2000 - Combinational Logic - 13 X' + Y' 1 1 1 0

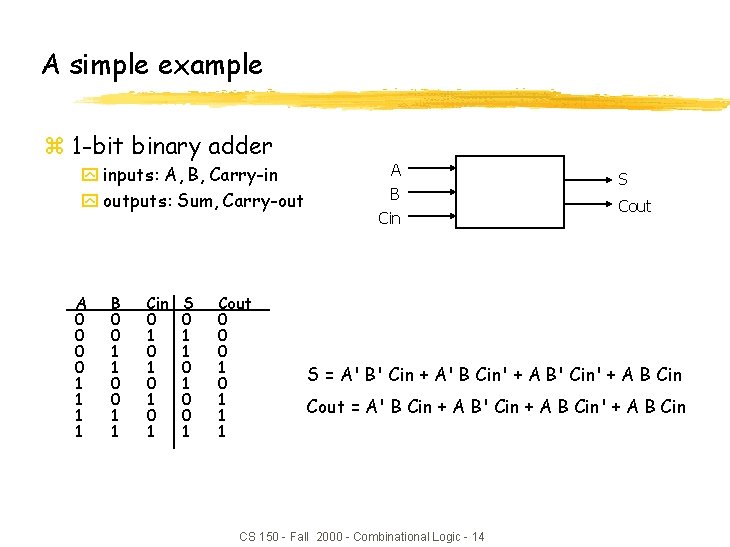
A simple example z 1 -bit binary adder y inputs: A, B, Carry-in y outputs: Sum, Carry-out A 0 0 1 1 B 0 0 1 1 Cin 0 1 0 1 S 0 1 1 0 0 1 Cout 0 0 0 1 1 1 A B Cin S Cout S = A' B' Cin + A' B Cin' + A B' Cin' + A B Cin Cout = A' B Cin + A B' Cin + A B Cin' + A B Cin CS 150 - Fall 2000 - Combinational Logic - 14

Apply theorems to simplify expressions z The theorems of Boolean algebra can simplify Boolean expressions y e. g. , full adder's carry-out function (same rules apply to any function) Cout = = = A' B Cin + A B' Cin + A B Cin' + A B Cin A' B Cin + A B' Cin + A B Cin' + A B Cin (A' + A) B Cin + A B' Cin + A B Cin' + A B Cin (1) B Cin + A B' Cin + A B Cin' + A B Cin + A (B' + B) Cin + A B Cin' + A B Cin + A (1) Cin + A B Cin' + A B Cin + A B (Cin' + Cin) B Cin + A B (1) B Cin + A B CS 150 - Fall 2000 - Combinational Logic - 15

From Boolean expressions to logic gates z NOT z AND z OR X + Y X' X X • Y XY X Y ~X X X 0 1 Y X Y X Y CS 150 - Fall 2000 - Combinational Logic - 16 Y 1 0 Z X 0 0 1 1 Y 0 1 Z 0 0 0 1 Z X 0 0 1 1 Y 0 1 Z 0 1 1 1

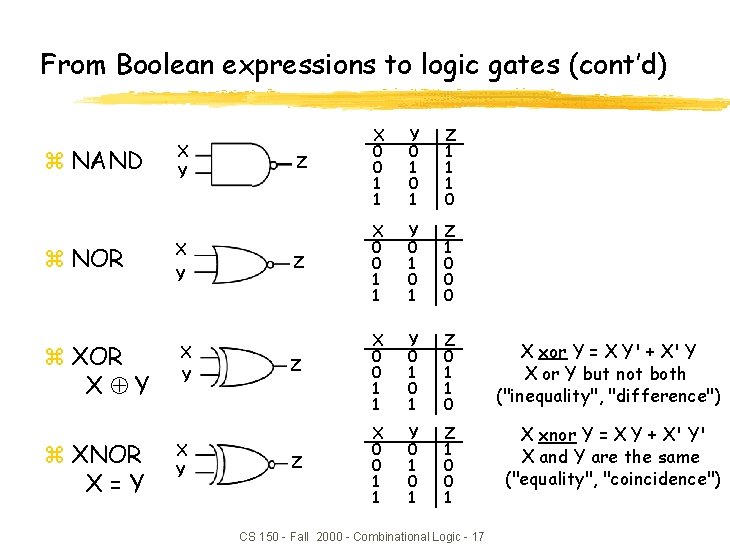
From Boolean expressions to logic gates (cont’d) z NAND z NOR z XOR X Y z XNOR X=Y X Y X Y Z X 0 0 1 1 Y 0 1 Z 1 1 1 0 Z X 0 0 1 1 Y 0 1 Z 1 0 0 0 Z X 0 0 1 1 Y 0 1 Z 0 1 1 0 Z X 0 0 1 1 Y 0 1 Z 1 0 0 1 CS 150 - Fall 2000 - Combinational Logic - 17 X xor Y = X Y' + X' Y X or Y but not both ("inequality", "difference") X xnor Y = X Y + X' Y' X and Y are the same ("equality", "coincidence")

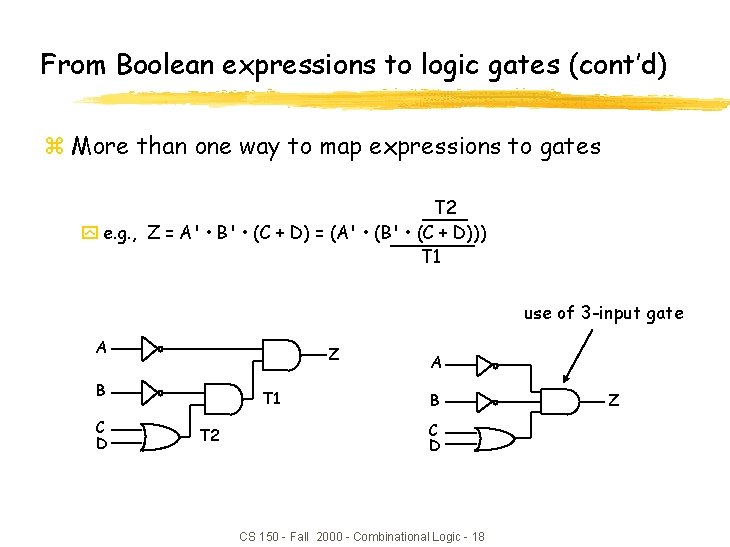
From Boolean expressions to logic gates (cont’d) z More than one way to map expressions to gates T 2 y e. g. , Z = A' • B' • (C + D) = (A' • (B' • (C + D))) T 1 use of 3 -input gate A Z B C D T 1 T 2 A B C D CS 150 - Fall 2000 - Combinational Logic - 18 Z

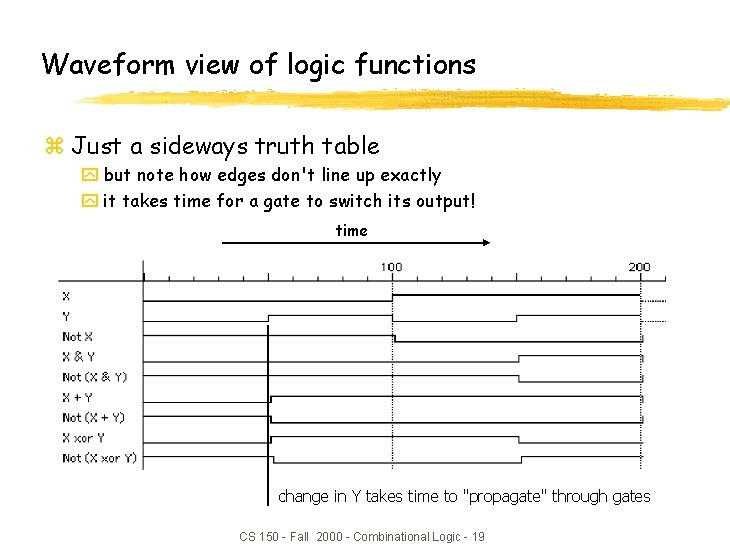
Waveform view of logic functions z Just a sideways truth table y but note how edges don't line up exactly y it takes time for a gate to switch its output! time change in Y takes time to "propagate" through gates CS 150 - Fall 2000 - Combinational Logic - 19

Choosing different realizations of a function A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 Z 0 1 0 1 1 0 two-level realization (we don't count NOT gates) multi-level realization (gates with fewer inputs) XOR gate (easier to draw but costlier to build) CS 150 - Fall 2000 - Combinational Logic - 20

Which realization is best? z Reduce number of inputs y literal: input variable (complemented or not) xcan approximate cost of logic gate as 2 transistors per literal xwhy not count inverters? y Fewer literals means less transistors xsmaller circuits y Fewer inputs implies faster gates xgates are smaller and thus also faster y Fan-ins (# of gate inputs) are limited in some technologies z Reduce number of gates y Fewer gates (and the packages they come in) means smaller circuits xdirectly influences manufacturing costs CS 150 - Fall 2000 - Combinational Logic - 21

Which is the best realization? (cont’d) z Reduce number of levels of gates y Fewer level of gates implies reduced signal propagation delays y Minimum delay configuration typically requires more gates xwider, less deep circuits z How do we explore tradeoffs between increased circuit delay and size? y Automated tools to generate different solutions y Logic minimization: reduce number of gates and complexity y Logic optimization: reduction while trading off against delay CS 150 - Fall 2000 - Combinational Logic - 22

Are all realizations equivalent? z Under the same input stimuli, the three alternative implementations have almost the same waveform behavior y delays are different y glitches (hazards) may arise y variations due to differences in number of gate levels and structure z Three implementations are functionally equivalent CS 150 - Fall 2000 - Combinational Logic - 23

Implementing Boolean functions z Technology independent y Canonical forms y Two-level forms y Multi-level forms z Technology choices y Packages of a few gates y Regular logic y Two-level programmable logic y Multi-level programmable logic CS 150 - Fall 2000 - Combinational Logic - 24

Canonical forms z Truth table is the unique signature of a Boolean function z Many alternative gate realizations may have the same truth table z Canonical forms y Standard forms for a Boolean expression y Provides a unique algebraic signature CS 150 - Fall 2000 - Combinational Logic - 25

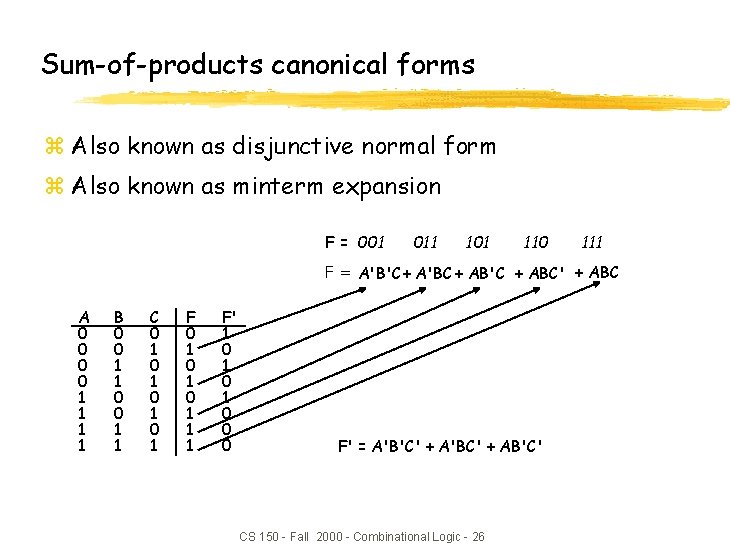
Sum-of-products canonical forms z Also known as disjunctive normal form z Also known as minterm expansion F = 001 011 101 110 111 F = A'B'C + A'BC + AB'C + ABC' + ABC A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 F 0 1 0 1 1 1 F' 1 0 1 0 0 0 F' = A'B'C' + A'BC' + AB'C' CS 150 - Fall 2000 - Combinational Logic - 26

Sum-of-products canonical form (cont’d) z Product term (or minterm) y ANDed product of literals – input combination for which output is true y Each variable appears exactly once, in true or inverted form (but not both) A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 minterms A'B'C' m 0 A'B'C m 1 A'BC' m 2 A'BC m 3 AB'C' m 4 AB'C m 5 ABC' m 6 ABC m 7 short-hand notation for minterms of 3 variables F in canonical form: F(A, B, C) = m(1, 3, 5, 6, 7) = m 1 + m 3 + m 5 + m 6 + m 7 = A'B'C + A'BC + AB'C + ABC' + ABC canonical form minimal form F(A, B, C) = A'B'C + A'BC + AB'C + ABC' = (A'B' + A'B + AB' + AB)C + ABC' = ((A' + A)(B' + B))C + ABC' = ABC' + C = AB + C CS 150 - Fall 2000 - Combinational Logic - 27

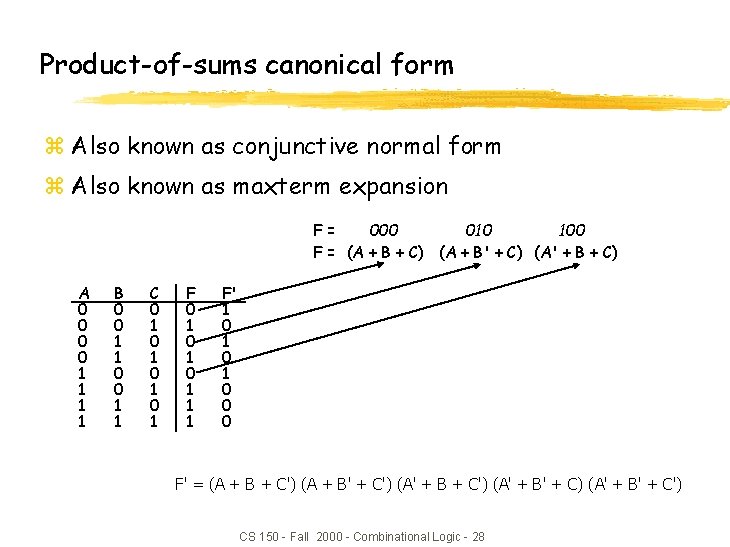
Product-of-sums canonical form z Also known as conjunctive normal form z Also known as maxterm expansion F= 000 010 100 F = (A + B + C) (A + B' + C) (A' + B + C) A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 F 0 1 0 1 1 1 F' 1 0 1 0 0 0 F' = (A + B + C') (A + B' + C') (A' + B' + C) (A' + B' + C') CS 150 - Fall 2000 - Combinational Logic - 28

Product-of-sums canonical form (cont’d) z Sum term (or maxterm) y ORed sum of literals – input combination for which output is false y each variable appears exactly once, in true or inverted form (but not both) A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 maxterms A+B+C' A+B'+C' A'+B+C' A'+B'+C' M 0 M 1 M 2 M 3 M 4 M 5 M 6 M 7 F in canonical form: F(A, B, C) = M(0, 2, 4) = M 0 • M 2 • M 4 = (A + B + C) (A + B' + C) (A' + B + C) canonical form minimal form F(A, B, C) = (A + B + C) (A + B' + C) (A' + B + C) = (A + B + C) (A + B' + C) (A + B + C) (A' + B + C) = (A + C) (B + C) short-hand notation for maxterms of 3 variables CS 150 - Fall 2000 - Combinational Logic - 29

S-o-P, P-o-S, and de Morgan’s theorem z Sum-of-products y F' = A'B'C' + A'BC' + AB'C' z Apply de Morgan's y (F')' = (A'B'C' + A'BC' + AB'C')' y F = (A + B + C) (A + B' + C) (A' + B + C) z Product-of-sums y F' = (A + B + C') (A + B' + C') (A' + B' + C) (A' + B' + C') z Apply de Morgan's y (F')' = ( (A + B + C')(A + B' + C')(A' + B' + C)(A' + B' + C') )' y F = A'B'C + A'BC + AB'C + ABC' + ABC CS 150 - Fall 2000 - Combinational Logic - 30

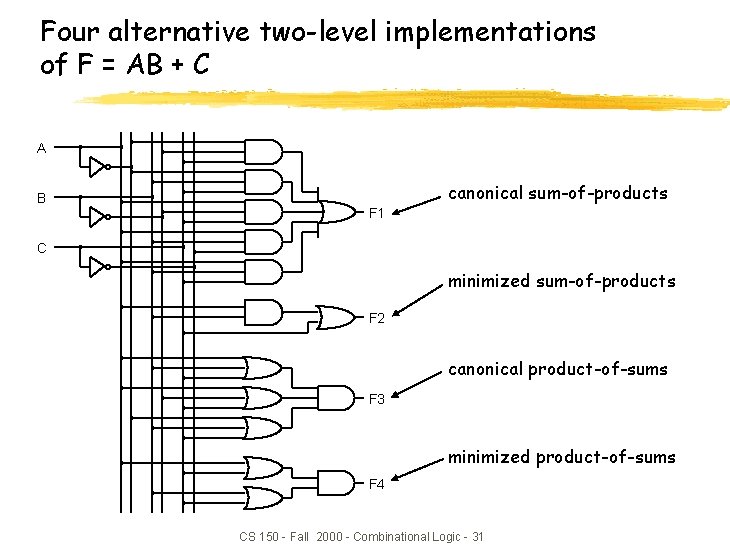
Four alternative two-level implementations of F = AB + C A B canonical sum-of-products F 1 C minimized sum-of-products F 2 canonical product-of-sums F 3 minimized product-of-sums F 4 CS 150 - Fall 2000 - Combinational Logic - 31

Waveforms for the four alternatives z Waveforms are essentially identical y Except for timing hazards (glitches) y Delays almost identical (modeled as a delay per level, not type of gate or number of inputs to gate) CS 150 - Fall 2000 - Combinational Logic - 32

Mapping between canonical forms z Minterm to maxterm conversion y Use maxterms whose indices do not appear in minterm expansion y e. g. , F(A, B, C) = m(1, 3, 5, 6, 7) = M(0, 2, 4) z Maxterm to minterm conversion y Use minterms whose indices do not appear in maxterm expansion y e. g. , F(A, B, C) = M(0, 2, 4) = m(1, 3, 5, 6, 7) z Minterm expansion of F to minterm expansion of F' y Use minterms whose indices do not appear y e. g. , F(A, B, C) = m(1, 3, 5, 6, 7) F'(A, B, C) = m(0, 2, 4) z Maxterm expansion of F to maxterm expansion of F' y Use maxterms whose indices do not appear y e. g. , F(A, B, C) = M(0, 2, 4) F'(A, B, C) = M(1, 3, 5, 6, 7) CS 150 - Fall 2000 - Combinational Logic - 33

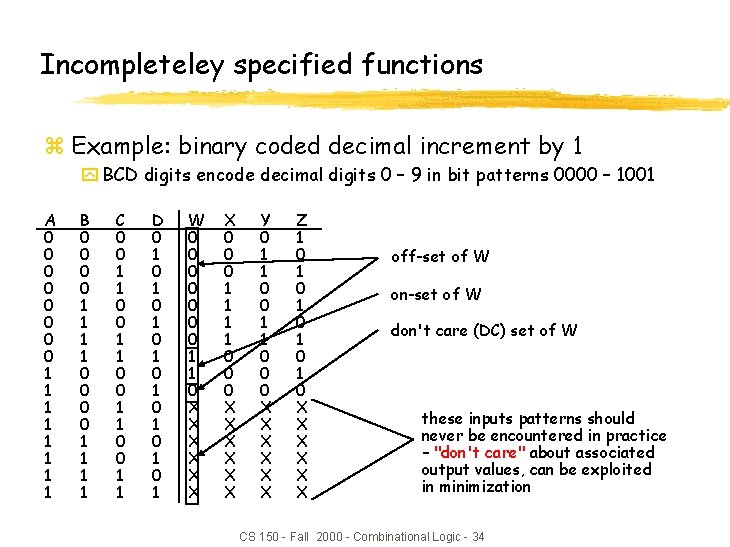
Incompleteley specified functions z Example: binary coded decimal increment by 1 y BCD digits encode decimal digits 0 – 9 in bit patterns 0000 – 1001 A 0 0 0 0 1 1 1 1 B 0 0 0 0 1 1 1 1 C 0 0 1 1 D 0 1 0 1 W 0 0 0 0 1 1 0 X X X X 0 0 0 1 1 0 0 0 X X X Y 0 1 1 0 0 0 X X X Z 1 0 1 0 1 0 X X X off-set of W on-set of W don't care (DC) set of W these inputs patterns should never be encountered in practice – "don't care" about associated output values, can be exploited in minimization CS 150 - Fall 2000 - Combinational Logic - 34

Notation for incompletely specified functions z Don't cares and canonical forms y So far, only represented on-set y Also represent don't-care-set y Need two of the three sets (on-set, off-set, dc-set) z Canonical representations of the BCD increment by 1 function: y Z = m 0 + m 2 + m 4 + m 6 + m 8 + d 10 + d 11 + d 12 + d 13 + d 14 + d 15 y Z = [ m(0, 2, 4, 6, 8) + d(10, 11, 12, 13, 14, 15) ] y Z = M 1 • M 3 • M 5 • M 7 • M 9 • D 10 • D 11 • D 12 • D 13 • D 14 • D 15 y Z = [ M(1, 3, 5, 7, 9) • D(10, 11, 12, 13, 14, 15) ] CS 150 - Fall 2000 - Combinational Logic - 35

Simplification of two-level combinational logic z Finding a minimal sum of products or product of sums realization y Exploit don't care information in the process z Algebraic simplification y Not an algorithmic/systematic procedure y How do you know when the minimum realization has been found? z Computer-aided design tools y Precise solutions require very long computation times, especially for functions with many inputs (> 10) y Heuristic methods employed – "educated guesses" to reduce amount of computation and yield good if not best solutions z Hand methods still relevant y To understand automatic tools and their strengths and weaknesses y Ability to check results (on small examples) CS 150 - Fall 2000 - Combinational Logic - 36

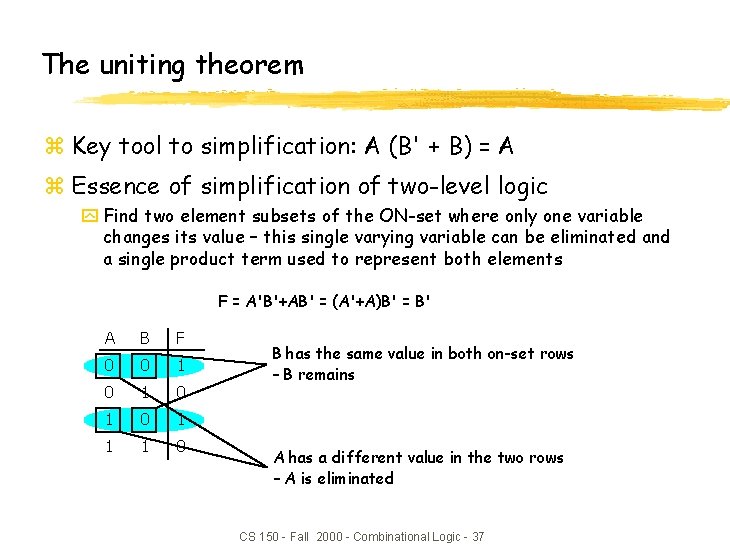
The uniting theorem z Key tool to simplification: A (B' + B) = A z Essence of simplification of two-level logic y Find two element subsets of the ON-set where only one variable changes its value – this single varying variable can be eliminated and a single product term used to represent both elements F = A'B'+AB' = (A'+A)B' = B' A B F 0 0 1 0 1 1 1 0 B has the same value in both on-set rows – B remains A has a different value in the two rows – A is eliminated CS 150 - Fall 2000 - Combinational Logic - 37

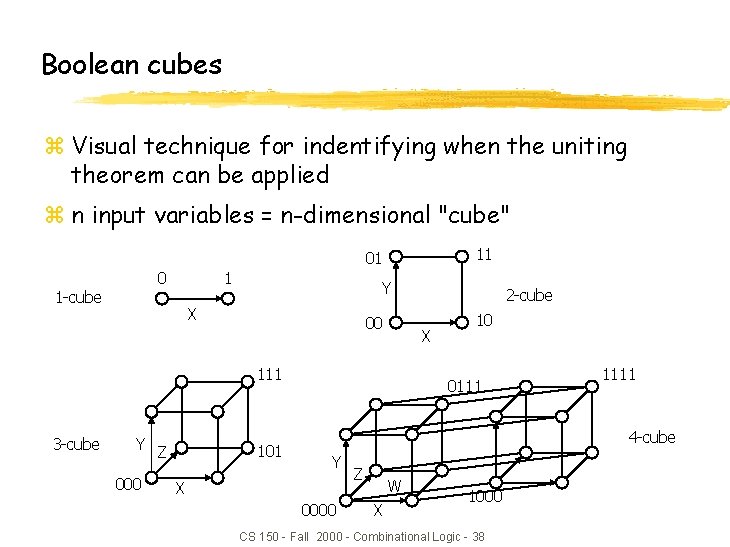
Boolean cubes z Visual technique for indentifying when the uniting theorem can be applied z n input variables = n-dimensional "cube" 11 01 0 1 -cube 1 Y X 00 X 111 3 -cube Y Z 000 101 2 -cube 10 0111 1111 4 -cube Y X 0000 Z W X 1000 CS 150 - Fall 2000 - Combinational Logic - 38

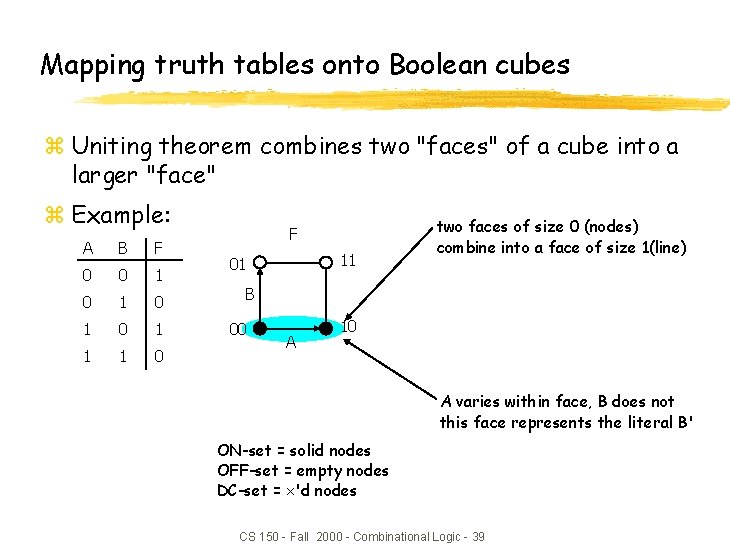
Mapping truth tables onto Boolean cubes z Uniting theorem combines two "faces" of a cube into a larger "face" z Example: A B F 0 0 1 0 1 1 1 0 F 11 01 two faces of size 0 (nodes) combine into a face of size 1(line) B 00 A 10 A varies within face, B does not this face represents the literal B' ON-set = solid nodes OFF-set = empty nodes DC-set = 'd nodes CS 150 - Fall 2000 - Combinational Logic - 39

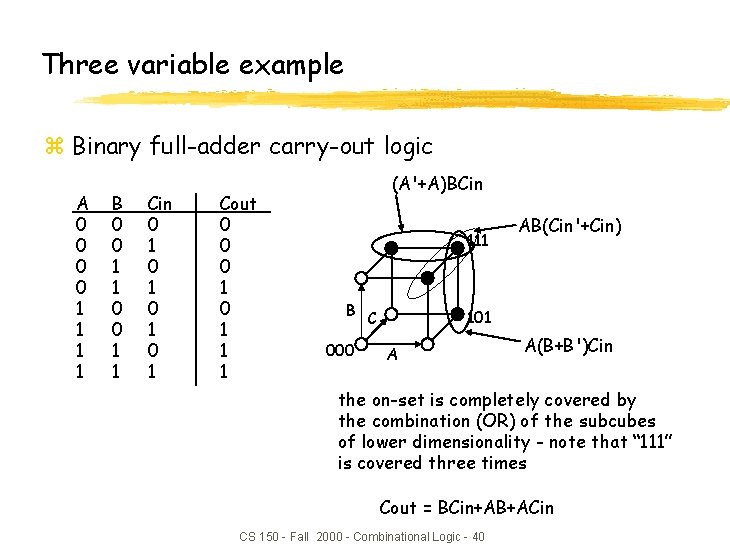
Three variable example z Binary full-adder carry-out logic A 0 0 1 1 B 0 0 1 1 Cin 0 1 0 1 Cout 0 0 0 1 1 1 (A'+A)BCin 111 B C 000 AB(Cin'+Cin) 101 A A(B+B')Cin the on-set is completely covered by the combination (OR) of the subcubes of lower dimensionality - note that “ 111” is covered three times Cout = BCin+AB+ACin CS 150 - Fall 2000 - Combinational Logic - 40

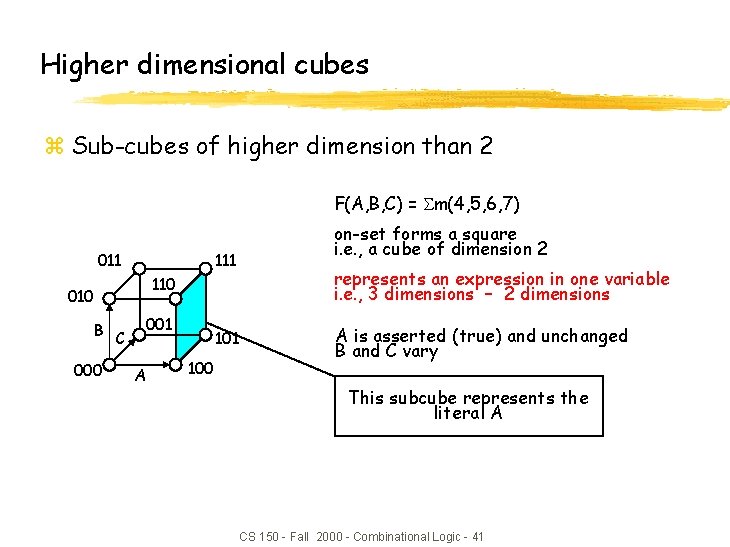
Higher dimensional cubes z Sub-cubes of higher dimension than 2 F(A, B, C) = m(4, 5, 6, 7) 011 on-set forms a square i. e. , a cube of dimension 2 111 represents an expression in one variable i. e. , 3 dimensions – 2 dimensions 110 010 B C 000 001 A 101 100 A is asserted (true) and unchanged B and C vary This subcube represents the literal A CS 150 - Fall 2000 - Combinational Logic - 41

m-dimensional cubes in a n-dimensional Boolean space z In a 3 -cube (three variables): y 0 -cube, i. e. , a single node, yields a term in 3 literals y 1 -cube, i. e. , a line of two nodes, yields a term in 2 literals y 2 -cube, i. e. , a plane of four nodes, yields a term in 1 literal y 3 -cube, i. e. , a cube of eight nodes, yields a constant term "1" z In general, y m-subcube within an n-cube (m < n) yields a term with n – m literals CS 150 - Fall 2000 - Combinational Logic - 42

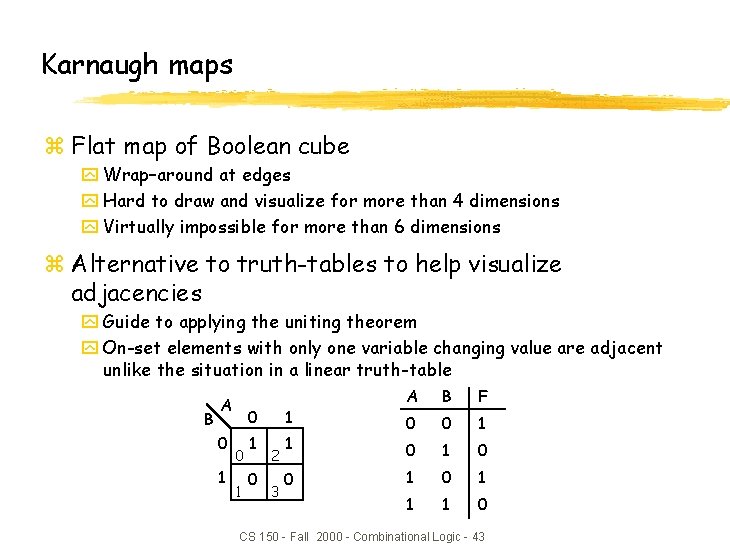
Karnaugh maps z Flat map of Boolean cube y Wrap–around at edges y Hard to draw and visualize for more than 4 dimensions y Virtually impossible for more than 6 dimensions z Alternative to truth-tables to help visualize adjacencies y Guide to applying the uniting theorem y On-set elements with only one variable changing value are adjacent unlike the situation in a linear truth-table B A 0 1 0 0 1 1 0 1 2 3 1 0 A B F 0 0 1 0 1 1 1 0 CS 150 - Fall 2000 - Combinational Logic - 43

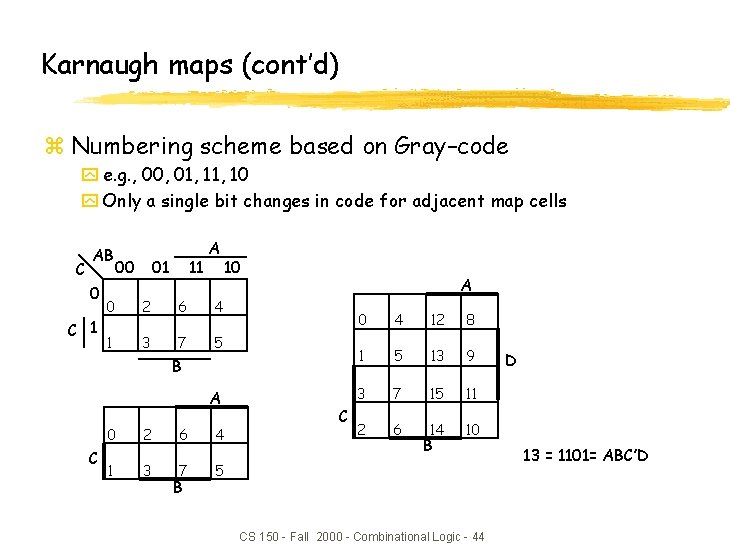
Karnaugh maps (cont’d) z Numbering scheme based on Gray–code y e. g. , 00, 01, 10 y Only a single bit changes in code for adjacent map cells C AB 0 C 1 00 11 01 A 0 2 6 4 1 3 7 5 10 A B A C 0 2 6 4 1 3 7 5 B C 0 4 12 8 1 5 13 9 3 7 15 11 2 6 14 10 B CS 150 - Fall 2000 - Combinational Logic - 44 D 13 = 1101= ABC’D

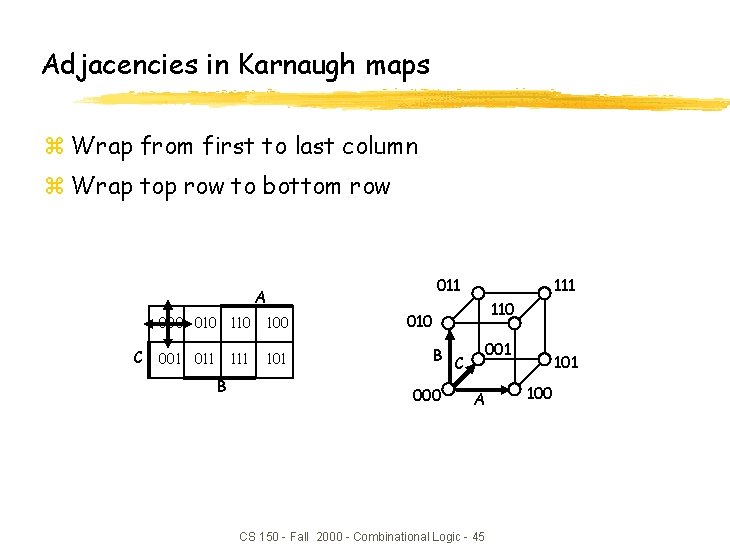
Adjacencies in Karnaugh maps z Wrap from first to last column z Wrap top row to bottom row 011 A 000 010 100 C 001 011 101 B 111 110 010 B C 000 001 A CS 150 - Fall 2000 - Combinational Logic - 45 101 100

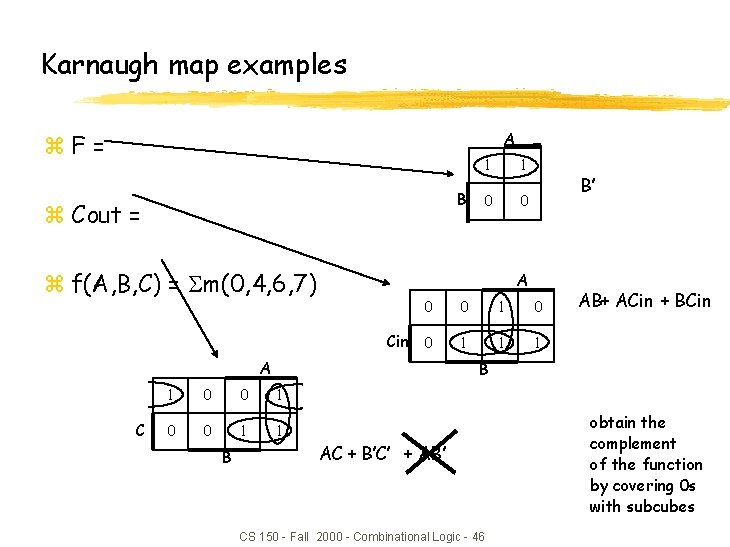
Karnaugh map examples A z. F= B z Cout = z f(A, B, C) = m(0, 4, 6, 7) 0 0 B’ 0 0 1 0 Cin 0 1 1 1 AB+ ACin + BCin B 1 0 0 1 1 B 1 A A C 1 AC + B’C’ + AB’ CS 150 - Fall 2000 - Combinational Logic - 46 obtain the complement of the function by covering 0 s with subcubes

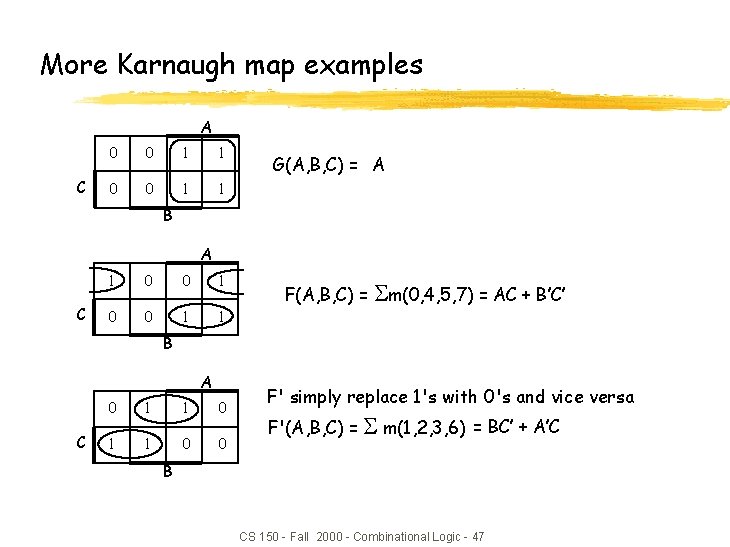
More Karnaugh map examples A C 0 0 1 1 G(A, B, C) = A B A C 1 0 0 1 1 F(A, B, C) = m(0, 4, 5, 7) = AC + B’C’ B A C 0 1 1 0 0 F' simply replace 1's with 0's and vice versa F'(A, B, C) = m(1, 2, 3, 6) = BC’ + A’C B CS 150 - Fall 2000 - Combinational Logic - 47

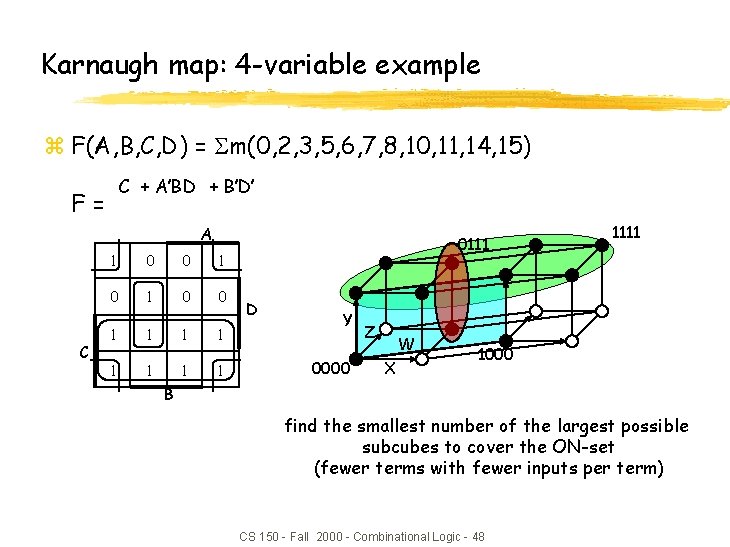
Karnaugh map: 4 -variable example z F(A, B, C, D) = m(0, 2, 3, 5, 6, 7, 8, 10, 11, 14, 15) C + A’BD + B’D’ F= A C 1 0 0 1 1 1 1 0111 D Y 0000 Z W X 1111 1000 B find the smallest number of the largest possible subcubes to cover the ON-set (fewer terms with fewer inputs per term) CS 150 - Fall 2000 - Combinational Logic - 48

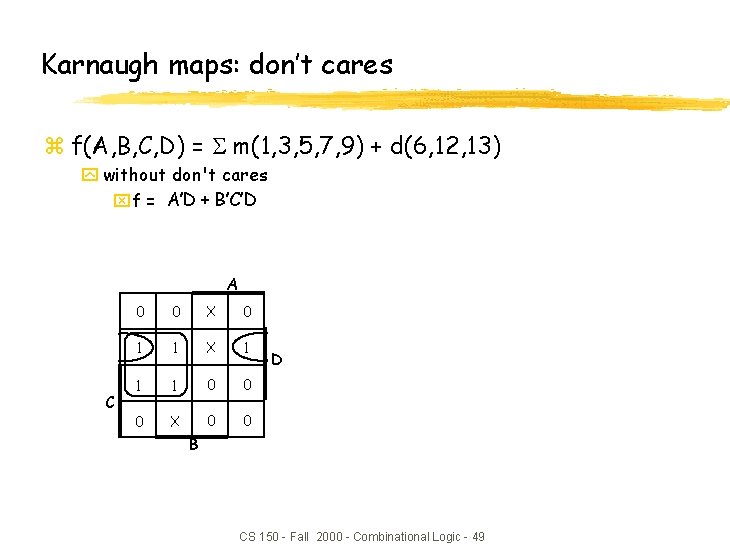
Karnaugh maps: don’t cares z f(A, B, C, D) = m(1, 3, 5, 7, 9) + d(6, 12, 13) y without don't cares xf = A’D + B’C’D A C 0 0 X 0 1 1 X 1 1 1 0 0 0 X 0 0 D B CS 150 - Fall 2000 - Combinational Logic - 49

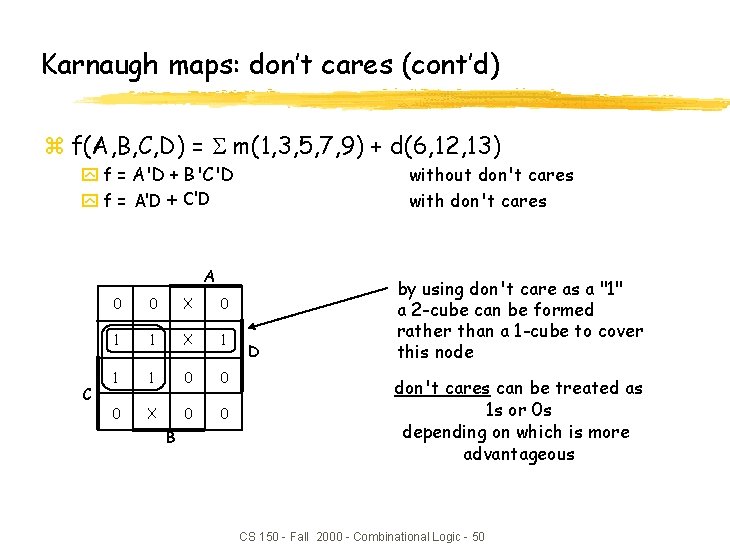
Karnaugh maps: don’t cares (cont’d) z f(A, B, C, D) = m(1, 3, 5, 7, 9) + d(6, 12, 13) y f = A'D + B'C'D y f = A'D + C'D without don't cares with don't cares A C 0 0 X 0 1 1 X 1 1 1 0 0 0 X 0 0 B D by using don't care as a "1" a 2 -cube can be formed rather than a 1 -cube to cover this node don't cares can be treated as 1 s or 0 s depending on which is more advantageous CS 150 - Fall 2000 - Combinational Logic - 50

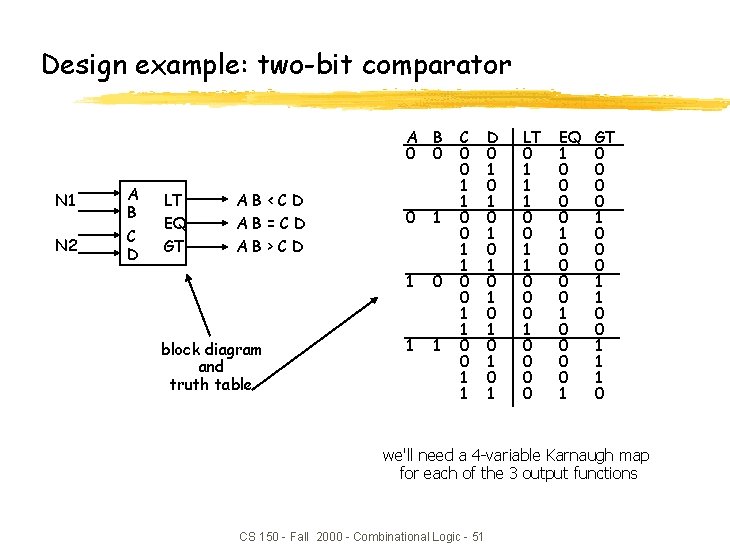
Design example: two-bit comparator A B 0 0 N 1 A B N 2 C D LT EQ GT AB<CD AB=CD AB>CD block diagram and truth table 0 1 1 C 0 0 1 1 D 0 1 0 1 LT 0 1 1 1 0 0 0 1 0 0 EQ 1 0 0 0 0 1 GT 0 0 1 0 0 0 1 1 1 0 we'll need a 4 -variable Karnaugh map for each of the 3 output functions CS 150 - Fall 2000 - Combinational Logic - 51

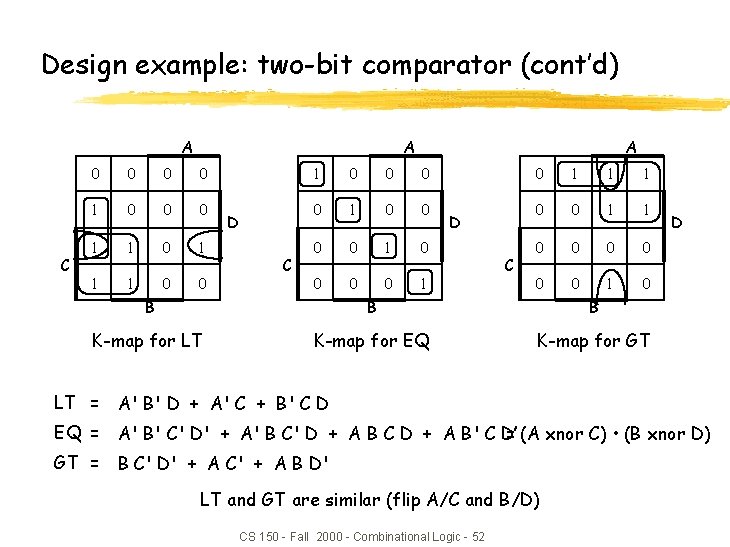
Design example: two-bit comparator (cont’d) A C A 0 0 1 0 0 0 1 1 1 0 0 D C A 1 0 0 0 0 1 D C 0 1 1 1 0 0 0 0 1 0 B B B K-map for LT K-map for EQ K-map for GT D LT = A' B' D + A' C + B' C D EQ = A' B' C' D' + A' B C' D + A B C D + A B' C D’ = (A xnor C) • (B xnor D) GT = B C' D' + A C' + A B D' LT and GT are similar (flip A/C and B/D) CS 150 - Fall 2000 - Combinational Logic - 52

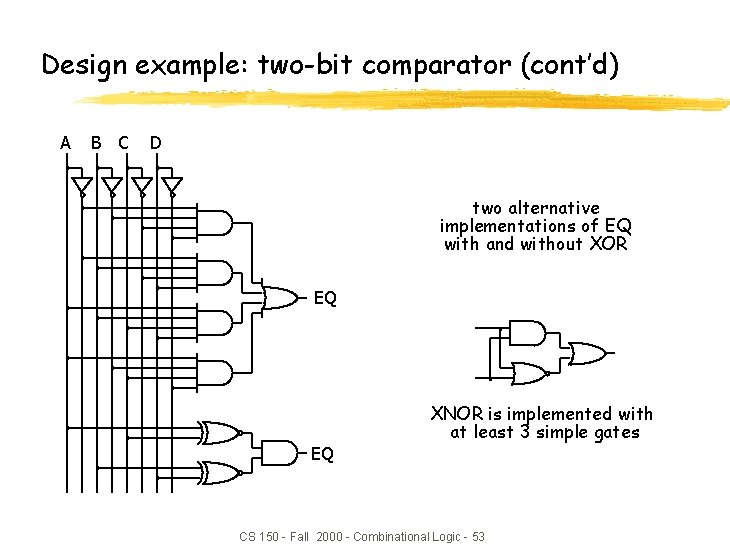
Design example: two-bit comparator (cont’d) A B C D two alternative implementations of EQ with and without XOR EQ EQ XNOR is implemented with at least 3 simple gates CS 150 - Fall 2000 - Combinational Logic - 53

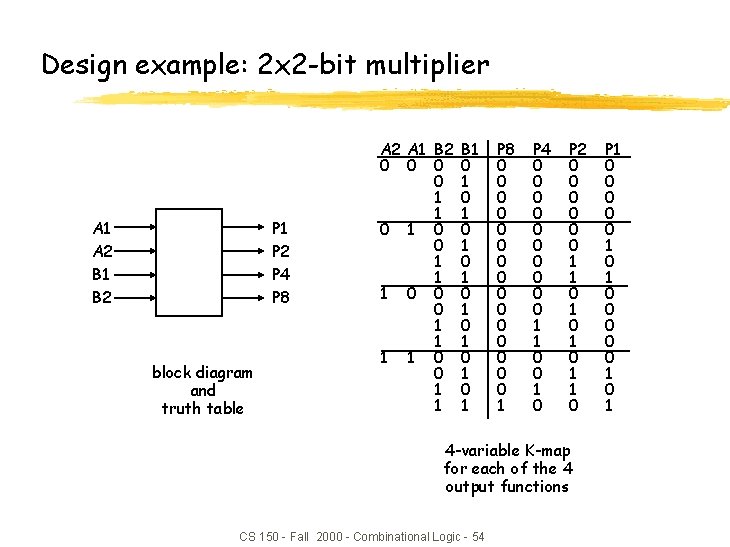
Design example: 2 x 2 -bit multiplier A 1 A 2 B 1 B 2 P 1 P 2 P 4 P 8 block diagram and truth table A 2 A 1 B 2 0 0 1 1 1 0 0 0 1 1 B 1 0 1 0 1 P 8 0 0 0 0 1 P 4 0 0 0 0 0 1 1 0 0 1 0 P 2 0 0 0 1 1 0 1 0 1 1 0 4 -variable K-map for each of the 4 output functions CS 150 - Fall 2000 - Combinational Logic - 54 P 1 0 0 0 0 0 1 0 1

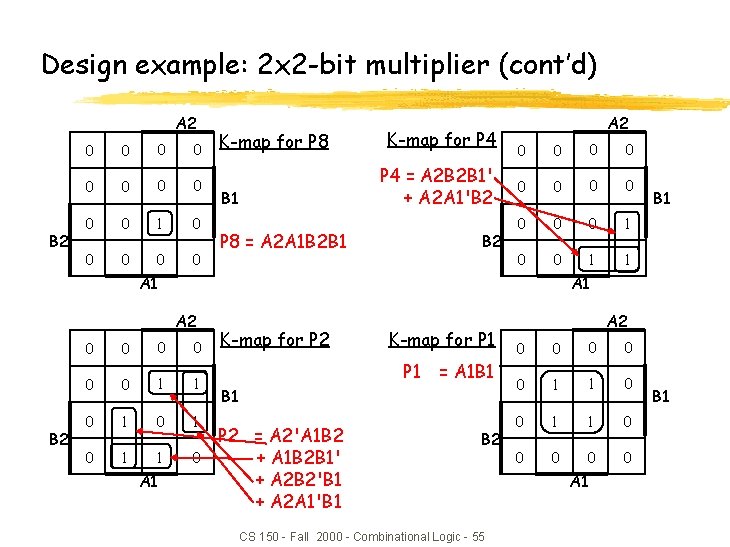
Design example: 2 x 2 -bit multiplier (cont’d) A 2 B 2 0 0 0 0 0 1 0 0 0 K-map for P 8 K-map for P 4 = A 2 B 2 B 1' + A 2 A 1'B 2 B 1 P 8 = A 2 A 1 B 2 B 1 B 2 A 2 0 0 0 1 0 0 1 1 A 1 A 2 B 2 0 0 0 1 1 0 1 0 1 1 0 A 1 B 1 K-map for P 2 K-map for P 1 = A 1 B 1 P 2 = A 2'A 1 B 2 + A 1 B 2 B 1' + A 2 B 2'B 1 + A 2 A 1'B 1 B 2 CS 150 - Fall 2000 - Combinational Logic - 55 A 2 0 0 0 1 1 0 0 0 A 1 B 1

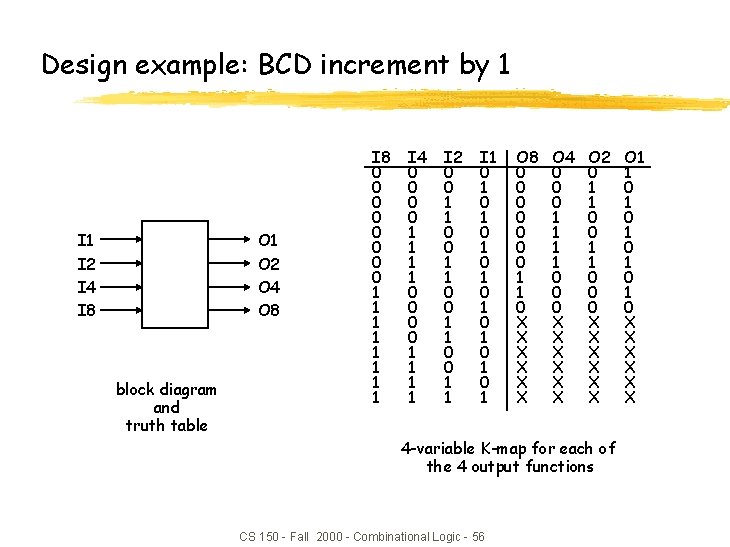
Design example: BCD increment by 1 I 2 I 4 I 8 O 1 O 2 O 4 O 8 block diagram and truth table I 8 0 0 0 0 1 1 1 1 I 4 0 0 0 0 1 1 1 1 I 2 0 0 1 1 I 1 0 1 0 1 O 8 0 0 0 0 1 1 0 X X X O 4 0 0 0 1 1 0 0 0 X X X O 2 0 1 1 0 0 0 X X X 4 -variable K-map for each of the 4 output functions CS 150 - Fall 2000 - Combinational Logic - 56 O 1 1 0 1 0 1 0 X X X

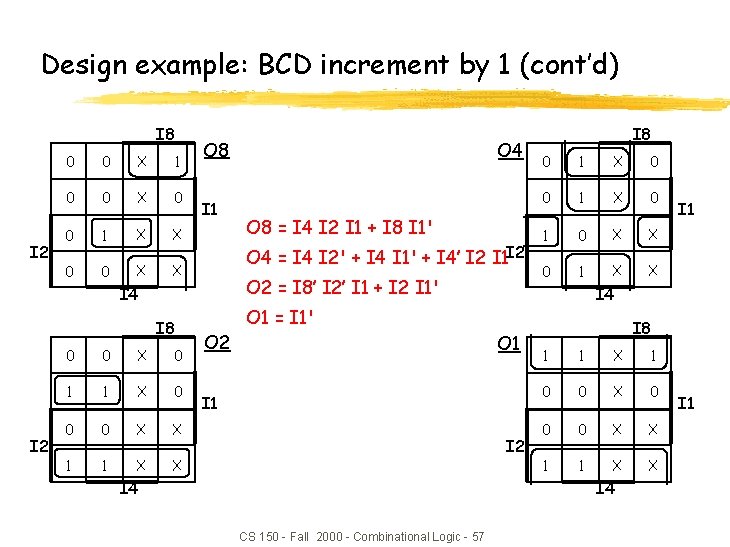
Design example: BCD increment by 1 (cont’d) I 8 I 2 0 0 X 1 0 0 X 0 0 1 X X 0 0 X X O 8 I 1 I 2 0 0 X 0 1 1 X 0 0 0 X X 1 1 X X O 8 = I 4 I 2 I 1 + I 8 I 1' O 4 = I 4 I 2' + I 4 I 1' + I 4’ I 2 I 1 I 2 O 2 = I 8’ I 2’ I 1 + I 2 I 1' I 4 I 8 O 4 O 2 I 8 0 1 X 0 1 0 X X 0 1 X X I 4 O 1 = I 1' O 1 I 2 I 4 I 8 1 1 X 1 0 0 X 0 0 0 X X 1 1 X X I 4 CS 150 - Fall 2000 - Combinational Logic - 57 I 1

Definition of terms for two-level simplification z Implicant y Single element of ON-set or DC-set or any group of these elements that can be combined to form a subcube z Prime implicant y Implicant that can't be combined with another to form a larger subcube z Essential prime implicant y Prime implicant is essential if it alone covers an element of ON-set y Will participate in ALL possible covers of the ON-set y DC-set used to form prime implicants but not to make implicant essential z Objective: y Grow implicant into prime implicants (minimize literals per term) y Cover the ON-set with as few prime implicants as possible (minimize number of product terms) CS 150 - Fall 2000 - Combinational Logic - 58

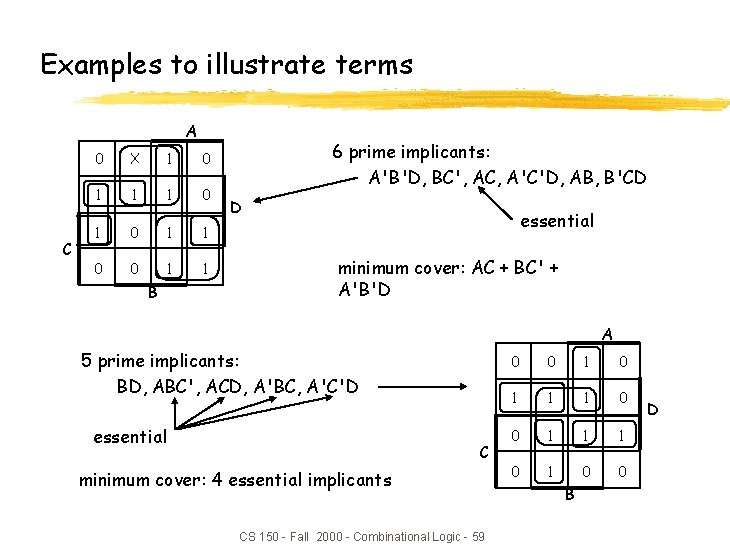
Examples to illustrate terms A C 0 X 1 0 1 1 0 0 1 1 B 6 prime implicants: A'B'D, BC', AC, A'C'D, AB, B'CD D essential minimum cover: AC + BC' + A'B'D A 5 prime implicants: BD, ABC', ACD, A'BC, A'C'D essential C minimum cover: 4 essential implicants CS 150 - Fall 2000 - Combinational Logic - 59 0 0 1 1 1 0 0 B D

Algorithm for two-level simplification z Algorithm: minimum sum-of-products expression from a Karnaugh map y Step 1: choose an element of the ON-set y Step 2: find "maximal" groupings of 1 s and Xs adjacent to that element xconsider top/bottom row, left/right column, and corner adjacencies xthis forms prime implicants (number of elements always a power of 2) y Repeat Steps 1 and 2 to find all prime implicants y Step 3: revisit the 1 s in the K-map xif covered by single prime implicant, it is essential, and participates in final cover x 1 s covered by essential prime implicant do not need to be revisited y Step 4: if there remain 1 s not covered by essential prime implicants xselect the smallest number of prime implicants that cover the remaining 1 s CS 150 - Fall 2000 - Combinational Logic - 60

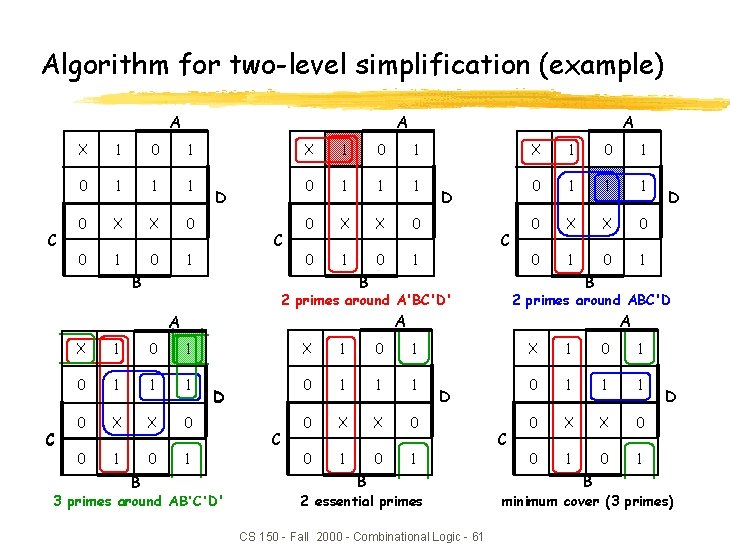
Algorithm for two-level simplification (example) A A C X 1 0 1 1 1 0 X X 0 0 1 D C X 1 0 1 0 1 1 1 0 X X 0 0 1 0 1 2 primes around ABC'D A X 1 0 1 1 1 0 X X 0 0 1 D 3 primes around AB'C'D' C D B 2 primes around A'BC'D' A B D B B C A A X 1 0 1 1 1 0 X X 0 0 1 D B 2 essential primes CS 150 - Fall 2000 - Combinational Logic - 61 C X 1 0 1 1 1 0 X X 0 0 1 B D minimum cover (3 primes)

Combinational logic summary z Logic functions, truth tables, and switches y NOT, AND, OR, NAND, NOR, XOR, . . . , minimal set z Axioms and theorems of Boolean algebra y Proofs by re-writing and perfect induction z Gate logic y Networks of Boolean functions and their time behavior z Canonical forms y Two-level and incompletely specified functions z Simplification y Two-level simplification z Later y Automation of simplification y Multi-level logic y Design case studies y Time behavior CS 150 - Fall 2000 - Combinational Logic - 62