Boolean Algebra 91509 L 5 Boolean Algebra Copyright

Boolean Algebra 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 1

Class 5 outline o Boolean Algebra n n n o Basic Boolean Equations Multiple Level Logic Representation Basic Identities Algebraic Manipulation Complements and Duals Material from section 2 -2 of text 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 2

History o George Boole n n o 2 November 1815 Lincolnshire, England – 8 December 1864 Ballintemple, Ireland Professor at Queens College, Cork, Ireland “spring of 1847 that he put his ideas into the pamphlet called Mathematical Analysis of Logic. ” from wikipedia. com 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 3

Basic Boolean Equations o o For the basic gates/functions AND n n n o 3 input gate 4 input gate OR n n o Z=AB X=CDE Y=FGHK Z=A+B Y=F+G+H+K 4 input gate NOT n n Z=A Y = (F G H K) 9/15/09 - L 5 Boolean Algebra actually 2 level logic Copyright 2009 - Joanne De. Groat, ECE, OSU 4

2 Level Logic o Consider the following logic equation n n Z(A, B, C, D) = A B + C D The Z(A, B, C, D) means that the output is a function of the four variables within the (). The AB and CD are terms of the expression. This form of representing the function is an algebraic expression. For this function to be True, either both A AND B are True OR both C AND D are True. 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 5
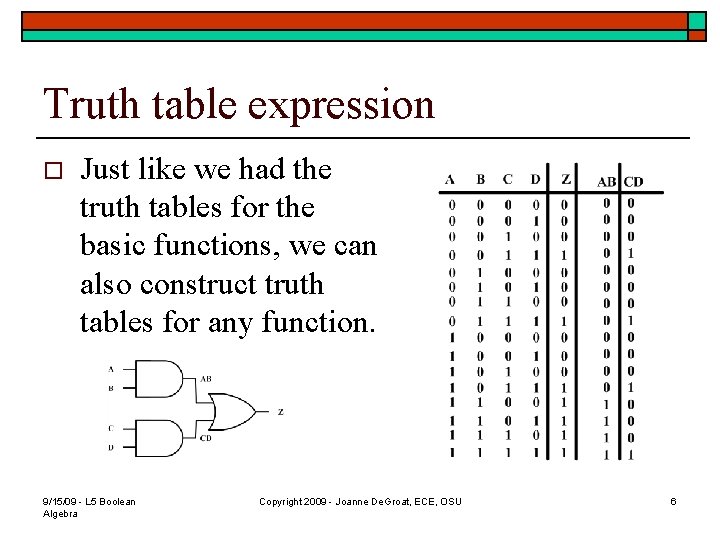
Truth table expression o Just like we had the truth tables for the basic functions, we can also construct truth tables for any function. 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 6

Examples of Boolean Equations o Some examples n n n F = AB + CD + BD’ Y = CD + A’B’ SUM = AB + A Cin + B Cin P = A 0 A 1 A 2 A 3 A 4 B 0 B 1 B 2 B 3 B 4 + … Equations can be very complex Usually desire a minimal expression 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 7

Basic Identities of Boolean Algebra o 1. X + 0 = X o o 3. X + 1 = 1 5. X + X = X o o 9/15/09 - L 5 Boolean Algebra o 2. X · 1 = X 4. X · 0 = 0 6. X · X = X Copyright 2009 - Joanne De. Groat, ECE, OSU 8

Basic Identities (2) o 7. X + X’ = 1 o 9. (X’)’ = X 9/15/09 - L 5 Boolean Algebra o 8. X · X’ = 0 Copyright 2009 - Joanne De. Groat, ECE, OSU 9

Basic Properties (Laws) o Commutative n o 10. X + Y = Y + X Associative n o o n n n o 12. X+(Y+Z)=(X+Y)+Z Distributive 9/15/09 - L 5 Boolean Algebra 11. X · Y = Y · X Associative n o 14. X(Y+Z) =XY+XZ AND distributes over OR Commutative 13. X(YZ) = (XY)Z Distributive n n 15. X+YZ=(X+Y)(X+Z) OR distributes over AND Copyright 2009 - Joanne De. Groat, ECE, OSU 10

Basic Properties (2) o o De. Morgan’s Theorem Very important in simplifying equations n n 16. (X + Y)’ = X’ · Y’ 17. (XY)’ = X’ + Y’ 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 11

Simplify, simplify o These properties (Laws and Theorems) can be used to simplify equations to their simplest form. n Simplify 9/15/09 - L 5 Boolean Algebra F=X’YZ+X’YZ’+XZ Copyright 2009 - Joanne De. Groat, ECE, OSU 12
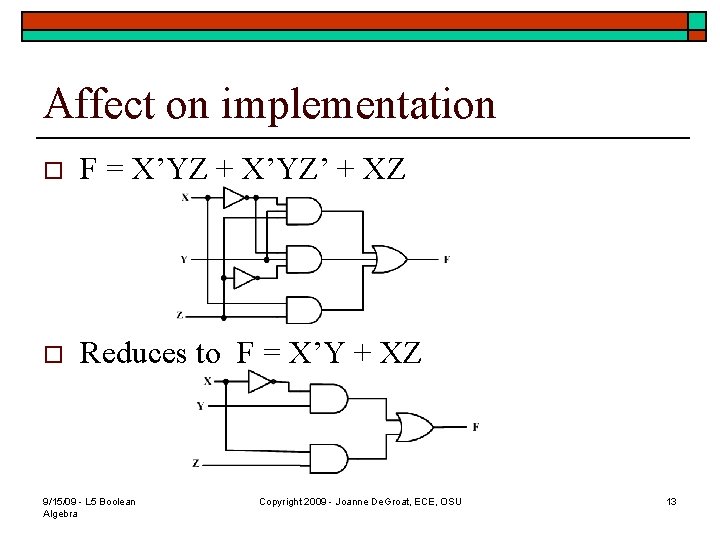
Affect on implementation o F = X’YZ + X’YZ’ + XZ o Reduces to F = X’Y + XZ 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 13

Other examples o Examples from the text n 1. X + XY = X· 1 + XY = X(1+Y) = X· 1 = X o n 2 14 3 2 2. XY+XY’ = X(Y + Y’) = X· 1 = X o n Use 14 7 2 3. X+X’Y = (X+X’)(X+Y) = 1· (X+Y) = X+Y o 9/15/09 - L 5 Boolean Algebra Use 15 Copyright 2009 - Joanne De. Groat, ECE, OSU 7 2 14

Further Examples o Examples from the text n 4. X· (X+Y)=X·X+X·Y= X+XY=X(1+Y)=X· 1=X o n n Use 14 6 14 3 2 5. (X+Y) ·(X+Y’)=XX+XY’+XY+YY’= X+XY’+XY+0=X(1+Y’+Y)=X· 1=X by a slightly different reduction 6. X(X’+Y) = XX’+XY = 0 + XY = XY 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 15

Consensus Theorem o Theorem gives us the relationship n n n XY + X’Z + YZ = XY + X’Z Proof is on page 47. Note that in doing the reduction the first step is to and in a 1 to the YZ term. That 1 is in the form, (X+X’). 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 16

Application of Consensus Theorem o Consider (page 47 of text) n n n (A+B)(A’+C) = AA’ + AC + A’B + BC = AC + A’B 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 17

Complement of a function o In real implementation sometimes the complement of a function is needed. n Have 9/15/09 - L 5 Boolean Algebra F=X’YZ’+X’Y’Z Copyright 2009 - Joanne De. Groat, ECE, OSU 18

Duals o What is meant by the dual of a function? n o The dual of a function is obtained by interchanging OR and AND operations and replacing 1 s and 0 s with 0 s and 1 s. Shortcut to getting function complement n n Starting with the equation on the previous slide Generate the dual F=(X’+Y+Z’)(X’+Y’+Z) Complement each literal to get: F’=(X+Y’+Z)(X+Y+Z’) 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 19

Getting XILINX software o o Go to www. xilinx. com In the upper line you have n o o Sign in Language Documentation Downloads Choose Downloads On the right side of the page you will see n n “Logic design tools” Choose ISE Web. Pack. TM 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 20

Class 5 assignment o o Covered section 2 -2 Problems for hand in n o Problems for practice n o 2 -7 2 -2 a, b, c 2 -6 b, c, d Reading for next class: section 2 -3 9/15/09 - L 5 Boolean Algebra Copyright 2009 - Joanne De. Groat, ECE, OSU 21
- Slides: 21