Boolean Algebra Learning Objectives Learn that Boolean algebra

Boolean Algebra Learning Objectives • Learn that Boolean algebra produces a result that equals TRUE or FALSE • Learn how truth tables are used to represent Boolean expressions • Learn how to use the AND, OR and NOT operators on their own or grouped together. • Learn how to use NAND, NOR and XOR operators • Learn how to simplify Boolean expresssions • Learn how De Morgan’s Law allows Boolean expressions to be created using only NAND or NOR operators.

Boolean Algebra • Computers work essentially on logical instructions. • One way of demonstrating this is with Boolean Algebra and visually with Logic gates. A shorthand notation for a system of logic originally set forth by Aristotle and developed by George Boole (Boolean) is considering a set of statements either true or false. It is raining today A statement Possible Outcomes True False If the statement is represented by the variable X then you can say X Meaning True It is raining today False It is not raining today or X Meaning 1 It is raining today 0 It is not raining today

Boolean Algebra This is Boolean algebra – the concept of whether something is true or false. Since the introduction of digital electronics and computers which works with binary – a state of 0 s and 1 s – Boolean Algebra has now become very useful. Boolean Algebra can be represented in Truth Tables. Take this electronic diagram

Boolean Algebra Let transfer that diagram into a truth table. Switch Lamp Switch Closed Lamp Off Switch Closed Open Closed On False 0 0 True 1 1 OR Function The above was just stating that if this state is true then this happens. Now we are going to say if this is true OR this is true then this happens. Consider the following diagram. In programming terms this would be something like: IF (num 1 < 10 || num 1 > 20) ….
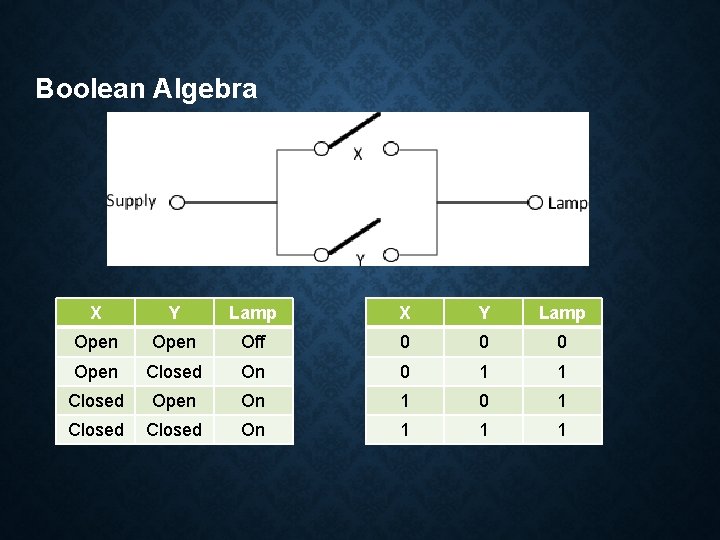
Boolean Algebra X Y Lamp Open Off 0 0 0 Open Closed On 0 1 1 Closed Open On 1 0 1 Closed On 1 1 1

Boolean Algebra This can be written in equation form X+Y=Q Where Q is a true setting for Lamp on. The + here means OR and not addition like in normal arithmetic. A truth table for the above will be the same as previous except that you replace the Lamp with Q. X Y Q 0 0 1 1 1 0 1 1 This can be shown in a black box diagram as: X Y OR Q

Boolean Algebra AND Function Consider the following diagram In this diagram both X and Y need to on or true for the lamp to be on. This is like saying that your fridge needs to be switched on and the door open for the light to come on. The equation syntax for this is to use a dot. So if Q is the lamp again. X. Y = Q And the truth table would look like this – In Programming terms: IF (num 1 > 10 && num 1 < 20) … X Y Q 0 0 1 1 1

Boolean Algebra NOT Function The not function can be stated as such: If a State P was true then R is false and vice versa. This can be put in a truth table like so: P R 0 1 1 0 From this we can state the P = NOT R – or the opposite of what R is. The syntax for this in equation form is this: _ P=R (note the _ over the R) Programming terms: IF (!valid) ….

Boolean Algebra Combinations of AND and OR You can use more complex Boolean algebra expressions by combining AND and ORs together. Consider the following diagram The notation for this can be written as: Q = (X AND Y) OR (X AND Z) or alternatively be written as: Q = X. Y + X. Z or Q = X. (Y + Z) Create a truth table for the above diagram.

Boolean Algebra NAND Function This is a combination of a NOT and an AND The notation would be something like this A. B Can you draw a truth table for a NAND Function

Boolean Algebra NOR Function This is a combination of a NOT and a OR The notation would be something like this A+B Can you draw a truth table for a NOR Function
Boolean Algebra XOR Function This function is true only if one value is true and not both. The notation would be something like this A B Can you draw a truth table for a NOR Function

Boolean Algebra Simplifying Boolean Expressions Some complex Boolean expressions can be simplified. This will enable circuitry to also be simplified in a computer. For instance Draw a truth table for the expression: (A. B) + A What do you think this can be simplified to? Task Use truth tables to show that the laws on table 30. 12 on page 251 are indeed the case. Put your answer in Specification Journal 19.

Boolean Algebra De Morgans Law This law is another way of simplifying Boolean equasions. 1) In a single expression invert all the ANDs to ORs and vice versa 2) Invert the whole expression – from NOT to normal and vice versa 3) Rule 1 – NOT (A AND B) is the same as (NOT A) OR (NOT B) 4) Rule 2 – NOT (A OR B) is the same as (NOT A) AND (NOT B) WORKING EXAMPLE
Boolean Algebra De Morgans Law Task Answer Question 4 on page 255 of the Text Book.
- Slides: 15