Algebra 1 boot camp Algebra and Modeling Day

Algebra 1 boot camp Algebra and Modeling Day 1

MAFS. 912. A-APR. 1. 1 D

MAFS. 912. A-APR. 1. 1

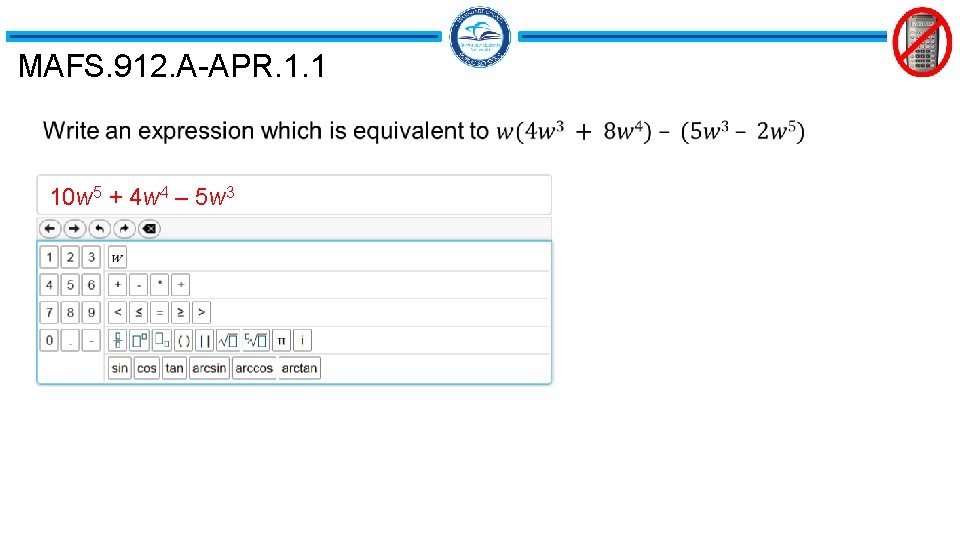
MAFS. 912. A-APR. 1. 1 10 w 5 + 4 w 4 – 5 w 3

MAFS. 912. A-APR. 1. 1

MAFS. 912. A-APR. 1. 1 C

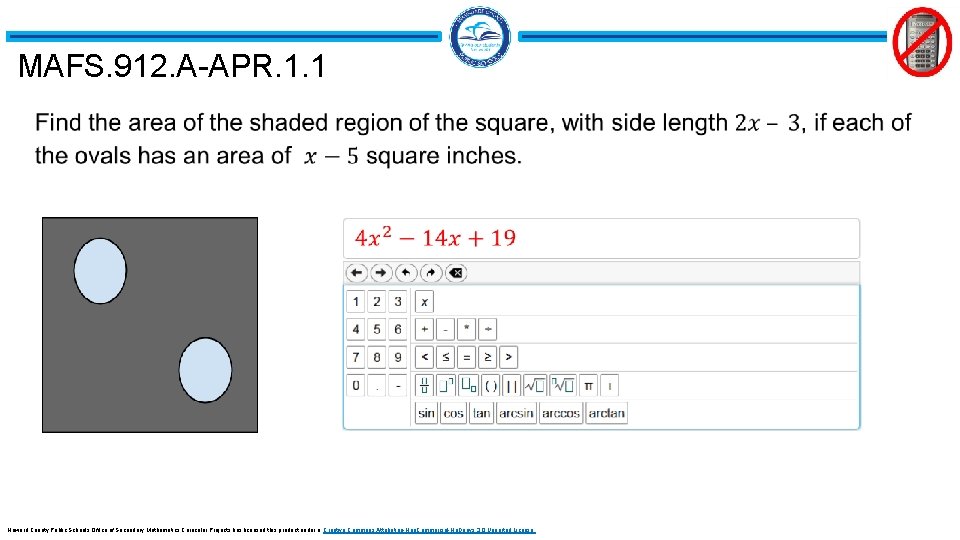
MAFS. 912. A-APR. 1. 1 Howard County Public Schools Office of Secondary Mathematics Curricular Projects has licensed this product under a Creative Commons Attribution-Non. Commercial-No. Derivs 3. 0 Unported License

MAFS. 912. A-APR. 1. 1

MAFS. 912. A-APR. 1. 1 Kiera claimed that the sum of two linear polynomials with rational coefficients is always a linear polynomial with rational coefficients. Drag the six statements into a logical sequence to outline an argument that proves this claim.

MAFS. 912. A-CED. 1. 1 A parking garage charges a base rate of $3. 50 for up to 2 hours, and an hourly rate for each additional hour. The sign below gives the prices for up to 5 hours of parking. Which linear equation can be used to find x, the additional hourly parking rate? C

MAFS. 912. A-CED. 1. 1 Kyran was given a check for $100 by his grandmother for his birthday, but had to promise her that he would invest the money in a bank until it had at least doubled in value. Kyran agreed, reluctantly, and found a bank where he could invest the $100 in a simple interest account that would gain 5% interest per year. If �� represents the number of years that Kyran will invest his money, which inequality could be used to find when he would have at least $200 in his account? B

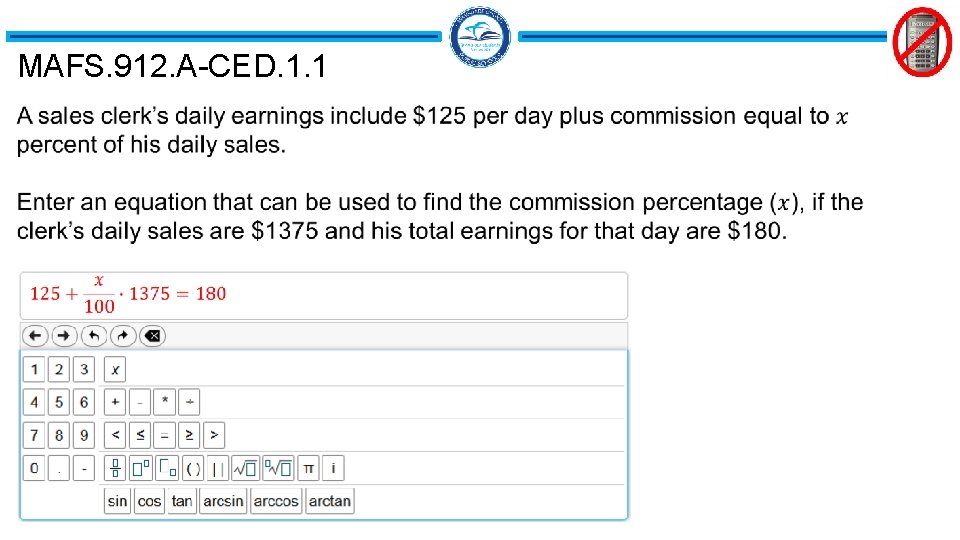
MAFS. 912. A-CED. 1. 1

MAFS. 912. A-CED. 1. 1 C

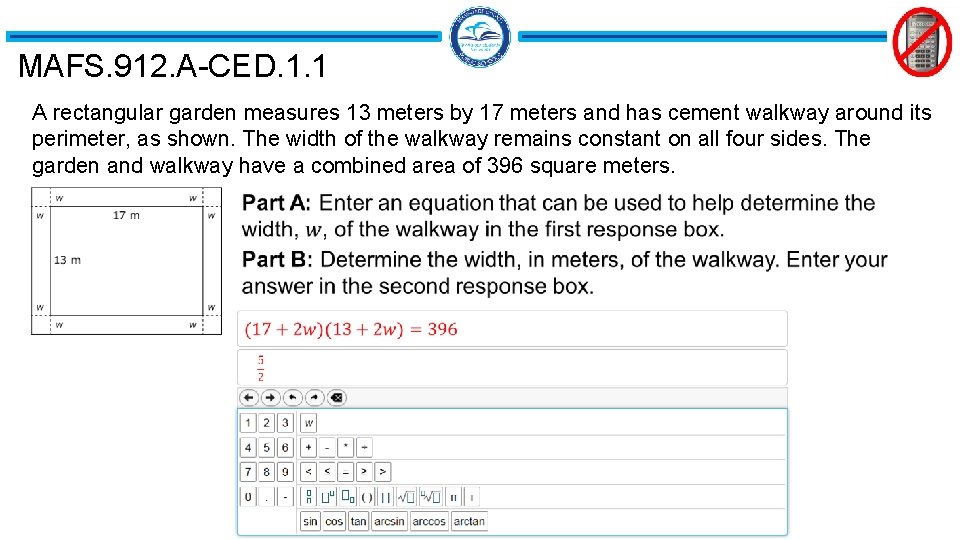
MAFS. 912. A-CED. 1. 1 A rectangular garden measures 13 meters by 17 meters and has cement walkway around its perimeter, as shown. The width of the walkway remains constant on all four sides. The garden and walkway have a combined area of 396 square meters.

MAFS. 912. A-CED. 1. 1 q Width: 4 in q Length: 4 in q Width: 6 in q Length: 6 in q Width: 7 in q Length: 7 in Length: 6 in, Width: 7 in

MAFS. 912. A-REI. 2. 3

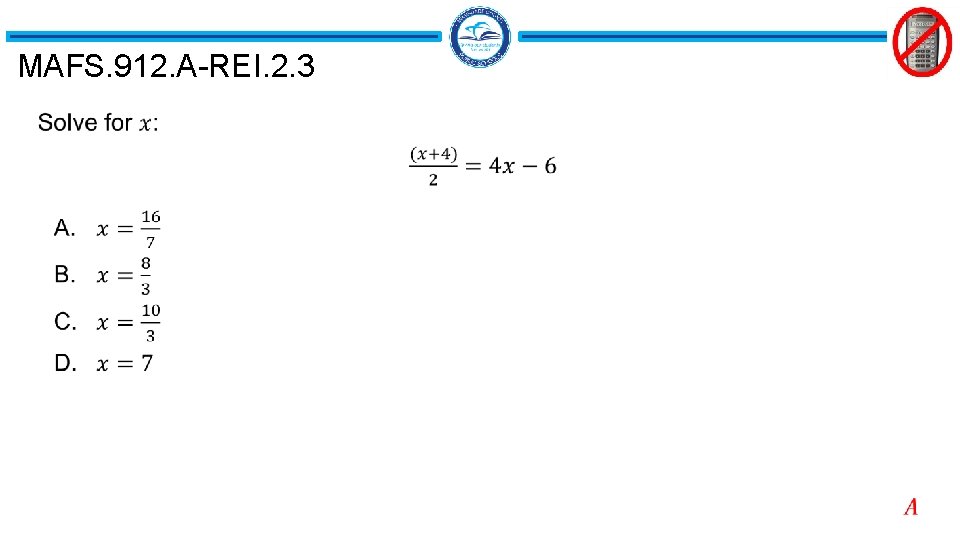
MAFS. 912. A-REI. 2. 3 Equation Yes No

MAFS. 912. A-CED. 1. 4

MAFS. 912. A-CED. 1. 2 An elementary school is having sand delivered for the playground. Sadie’s Sand charges $5. 00 per ton of sand plus a delivery fee of $200. Greg’s Sand Pit charges $12. 00 per ton of sand plus a delivery fee of $50. Use the graph below to represent functions that show the cost C of buying T tons of sand from each company.

MAFS. 912. A-CED. 1. 2

MAFS. 912. A-CED. 1. 2 A and D

MAFS. 912. A-CED. 1. 2 Meredith is purchasing a new toilet for her home. Toilet A costs $149 and uses approximately 380 gallons of water per month. Toilet B costs $169 and uses approximately 300 gallons of water per month. Water costs $2. 75 per 1000 gallons. Part A: Write a system of equations that models this situation. A. C. B. D. Part B: How many months will it take for Toilet B to be more cost effective?

MAFS. 912. A-CED. 1. 2 Malik and Nora are playing a video game. • Malik starts with m points and Nora starts n points. • Then Malik gets 150 more points, while Nora loses 50 points. • Finally, Nora gets a bonus and her score is doubled. • Nora now has 50 more points than Malik.

MAFS. 912. A-CED. 1. 2 Years Money in Bank 1 5, 665. 00 2 5, 834. 95 3 6, 009. 99 4 6, 190. 30 5 6, 376. 01 6 6, 567. 29

MAFS. 912. A-REI. 3. 5 Which system of equations has the same solution as the system below? A. B. C. D.

MAFS. 912. A-REI. 3. 5 A. B. C. D.

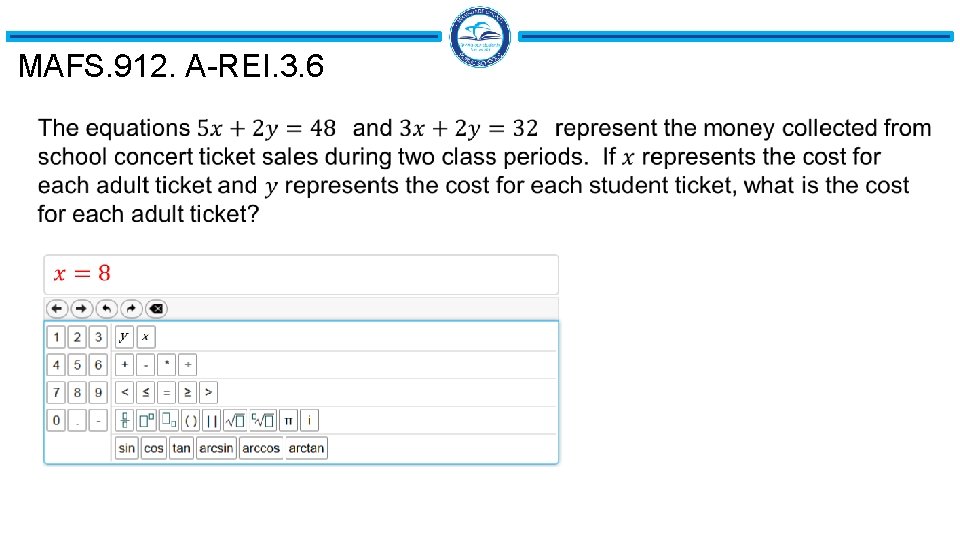
MAFS. 912. A-REI. 3. 6

MAFS. 912. A-REI. 3. 6 A restaurant serves a vegetarian and a chicken lunch special each day. Each vegetarian special is the same price. Each chicken special is the same price. However, the price of the vegetarian special is different from the price of the chicken special. • On Thursday, the restaurant collected $467 selling 21 vegetarian specials and 40 chicken specials. • On Friday, the restaurant collected $484 selling 28 vegetarian specials and 36 chicken specials. What is the cost, in dollars, of each lunch special?

MAFS. 912. A-REI. 3. 6 The basketball team sold t-shirts and hats as a fund-raiser. They sold a total of 23 items and made a profit of $246. They made a profit of $10 for every t-shirt they sold and $12 for every hat they sold. Determine the number of t-shirts and the number of hats the basketball team sold. • Enter the number of t-shirts in the first response box. • Enter the number of hats in the second response box.

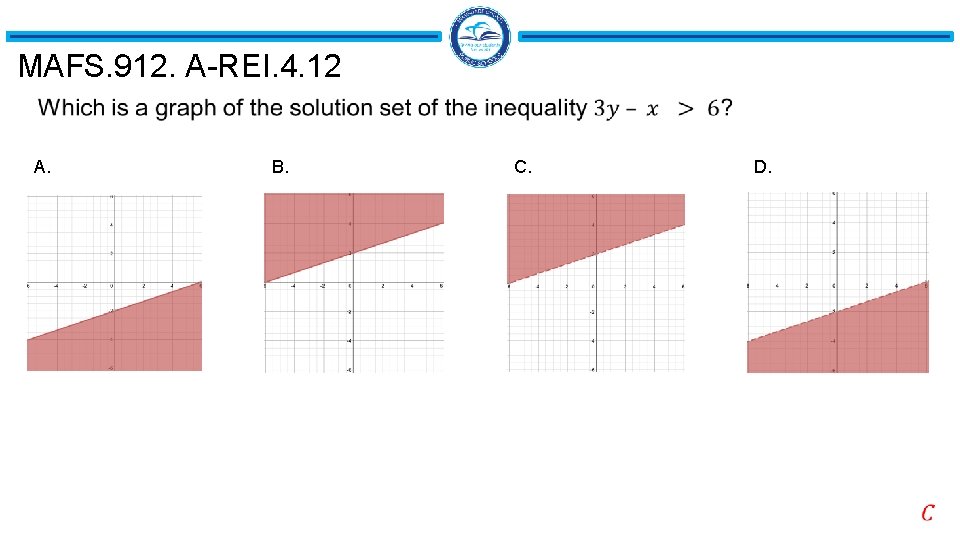
MAFS. 912. A-REI. 4. 12 A. B. C. D.

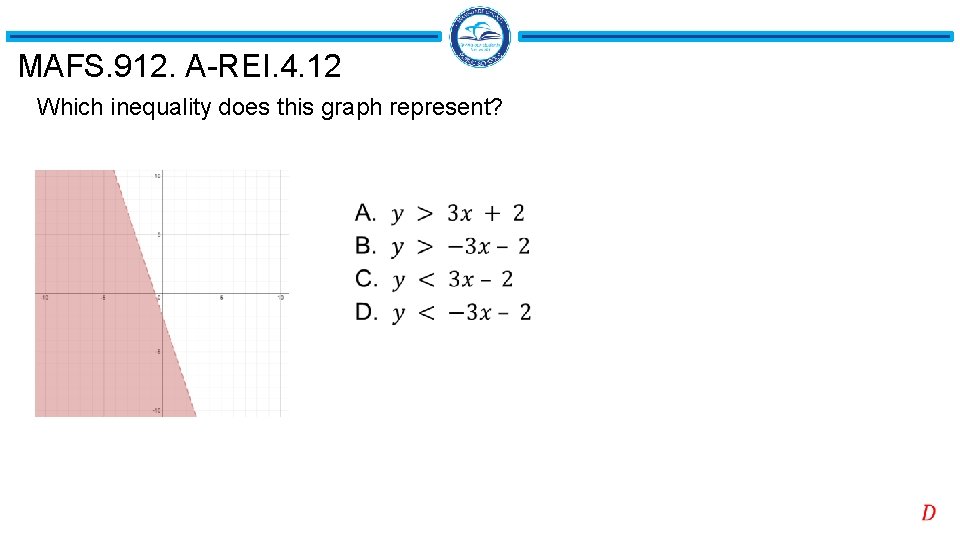
MAFS. 912. A-REI. 4. 12 Which inequality does this graph represent?

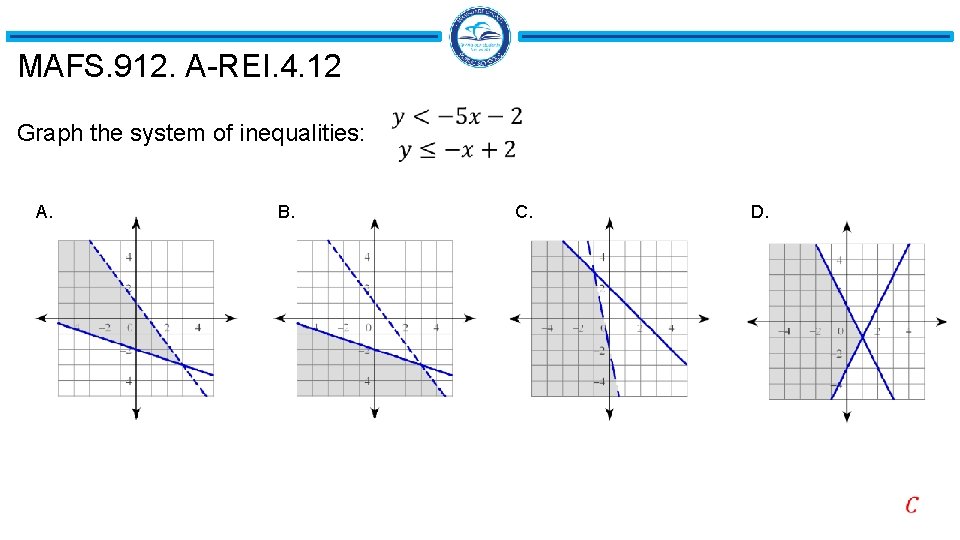
MAFS. 912. A-REI. 4. 12 Graph the system of inequalities: A. B. C. D.

MAFS. 912. A-REI. 4. 12 Determine the solution to the system of inequalities:

MAFS. 912. A-REI. 4. 12 The coordinate grid below shows points A through J. Given the system of inequalities shown below, select all the points that are solutions to this system of inequalities. q. A q. B q. C q. D q. E q. F q. G A , F, and G

MAFS. 912. A-CED. 1. 3 Part A: For what number of athletes would Part B: Is this a viable answer? Explain. both teams have the same number of Olympic medals? This answer is not a viable solution because you cannot have part of an athlete. 6. 5 athletes implies half an athlete, which is not possible in the context of the problem.

MAFS. 912. A-CED. 1. 3 David has two jobs. He earns $8 per hour babysitting his neighbor’s children and he earns $11 per hour working at the coffee shop. Part B: David worked 15 hours at the coffee shop. Use the inequality to find the number of full hours he must babysit to reach his goal of $200.

MAFS. 912. A-CED. 1. 3 In a community service program, students earn points for painting over graffiti and picking up trash. The following restrictions are imposed on the program: • A student may not serve more than 10 total hours per week; and • A student must serve at least 1 hour per week at each task. Part A: Which system represents the imposed Part B: Which numbers of hours spent painting constraints? over graffiti and hours spent picking up trash could fit the community service requirements? Select all A. C. that apply. q 3 graffiti hours and 4 trash hours q 6 graffiti hours and 7 trash hours q 8 graffiti hours and 3 trash hours B. D. q 9 graffiti hours and 1 trash hours q 0 graffiti hours and 10 trash hours A A, D, and F q 5 graffiti hours and 5 trash hours

MAFS. 912. A-REI. 1. 1 Step 1 Step 2 Step 3 Step 4 Step 5 Which property was used incorrectly when going from Step 2 to Step 3? A. B. C. D. Addition Property Distributive Property Substitution Property Transitive Property

MAFS. 912. A-REI. 1. 1 Step 1 Step 2 Step 3 Step 4 Step 5 Which step is the first incorrect step in Martha’s solution shown above? A. B. C. D. Step 2 Step 3 Step 4 Step 5

MAFS. 912. A-REI. 2. 4

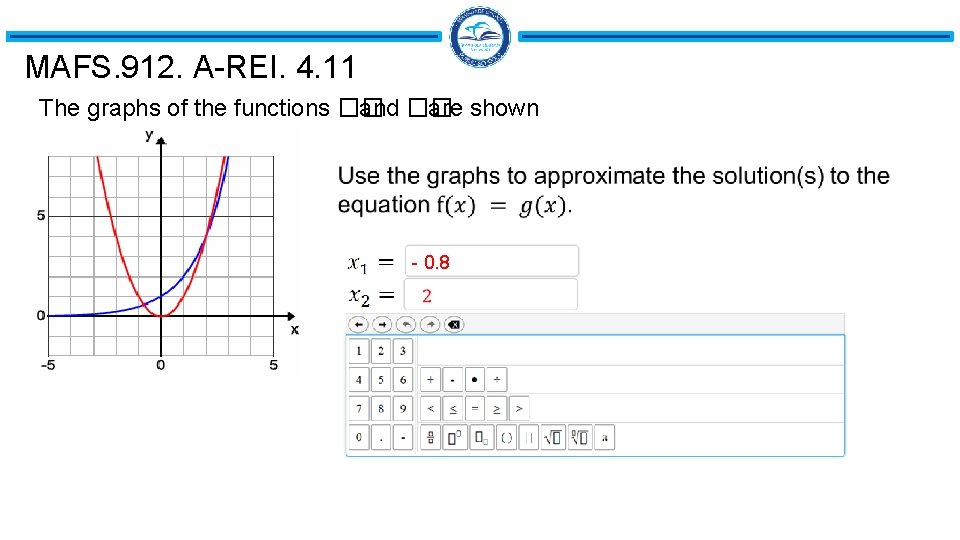
MAFS. 912. A-REI. 4. 11 The graphs of the functions �� and �� are shown - 0. 8

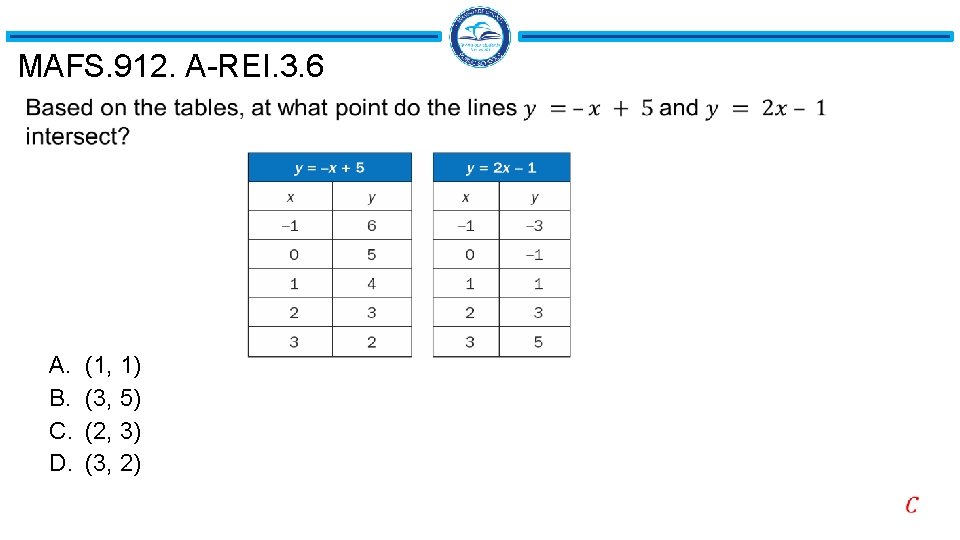
MAFS. 912. A-REI. 3. 6 A. B. C. D. (1, 1) (3, 5) (2, 3) (3, 2)

MAFS. 912. A-REI. 3. 6

MAFS. 912. A-REI. 4. 10 Choose the ordered pair that is a solution to the equation represented by the graph.

MAFS. 912. A-REI. 4. 10 q (-2, -10) q (-1, 1) q (0, 4) q (4, 8) q (6, 14) A, D, and E

MAFS. 912. A-REI. 4. 10 When is this statement true?

MAFS. 912. A-REI. 4. 10 Yes, it is a solution. Two raised to the power of 5 is equal 32.

MAFS. 912. A-REI. 4. 10

MAFS. 912. A-SSE. 2. 3 To complete the square, Arturo should have added 9 inside the parenthesis instead of subtracting 9. To keep the equation balanced he should have subtracted 9 instead of adding it. The correct minimum value of the function is 1.

MAFS. 912. A-SSE. 2. 3

MAFS. 912. A-SSE. 2. 3 Select all the equations with equivalent zeros. B and D

MAFS. 912. A-SSE. 2. 3

MAFS. 912. A-SSE. 2. 3 B

MAFS. 912. A-SSE. 1. 1

MAFS. 912. A-SSE. 1. 1 The total number of trips both trucks make to the job site. The total number of cubic yards that the two trucks deliver in one trip. The total number of cubic yards delivered to the job site.

MAFS. 912. A-SSE. 1. 1 Part A: Explain what the parameter 2, 400 represents in the equation of the function. The parameter 2, 400 represents the initial cost of the printer. Part B: What is the factor by which the printer depreciates each year? The factor is 0. 86. Part C: Amy also considered purchasing a printer that costs $4, 000 and depreciates by 25% each year. Which printer will have more value in 5 years? The printer that cost $2, 400 will have a better value by $179. 80

MAFS. 912. A. SSE. 1. 2