BOOLEAN ALGEBRA APPLICATIONS RELIABILITY OF CIRCUITS Boolean Algebra

BOOLEAN ALGEBRA APPLICATIONS RELIABILITY OF CIRCUITS Boolean Algebra Applications 1
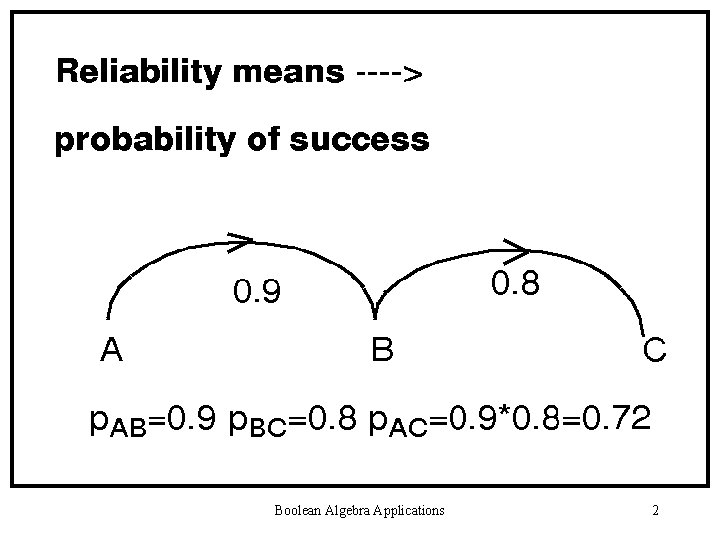
Boolean Algebra Applications 2
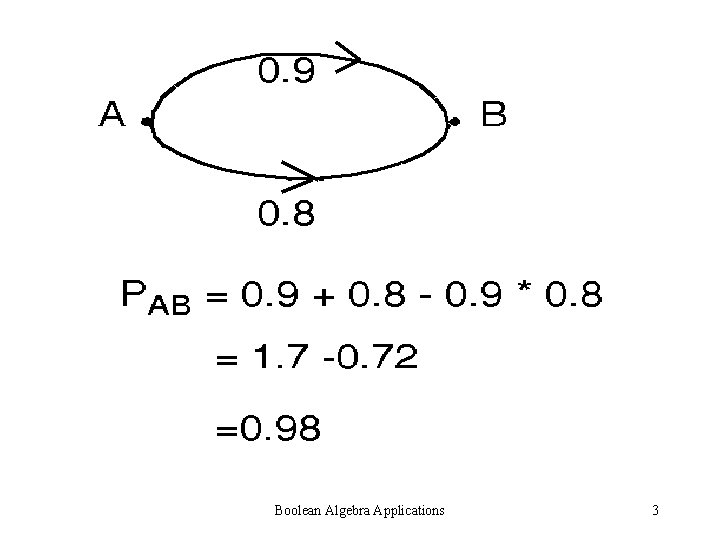
Boolean Algebra Applications 3
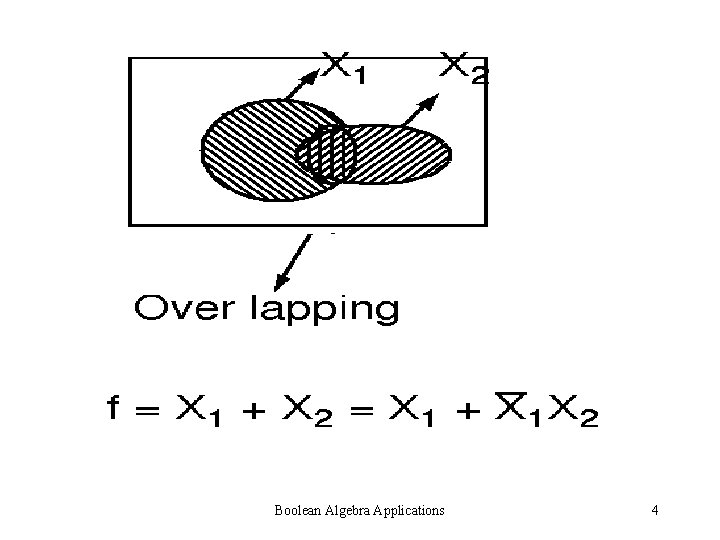
Boolean Algebra Applications 4
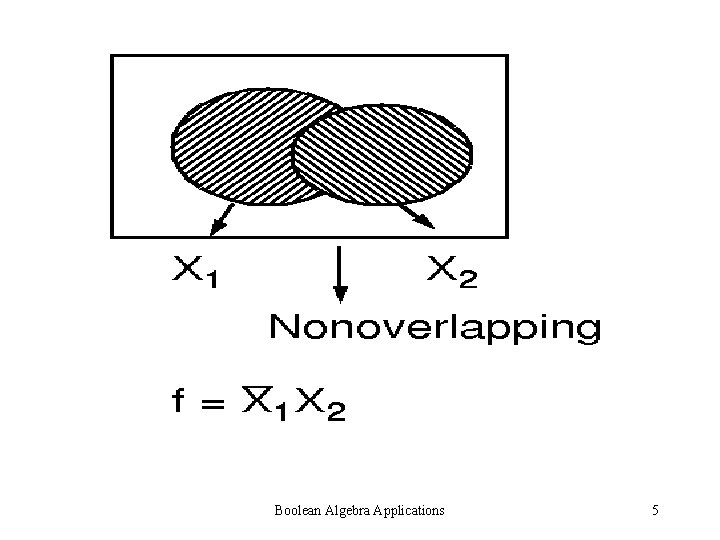
Boolean Algebra Applications 5

Boolean Algebra Applications 6
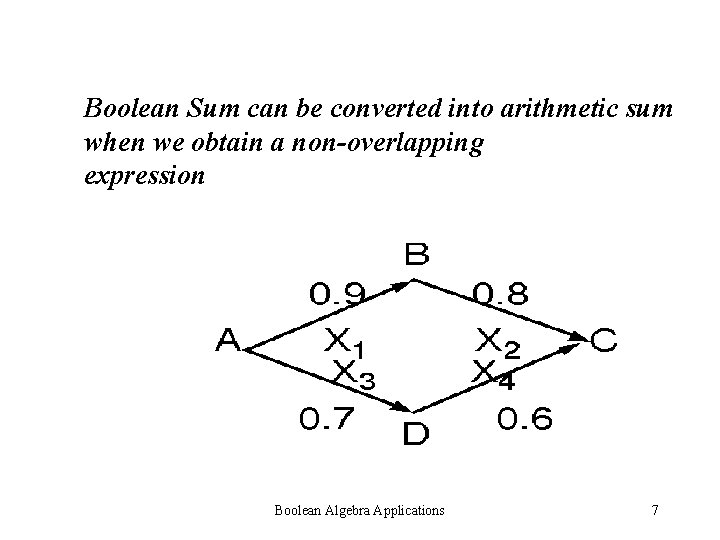
Boolean Sum can be converted into arithmetic sum when we obtain a non-overlapping expression Boolean Algebra Applications 7
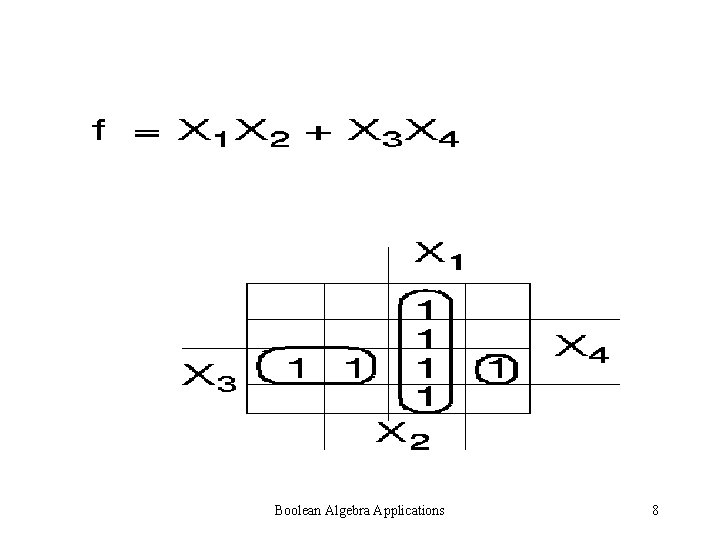
Boolean Algebra Applications 8
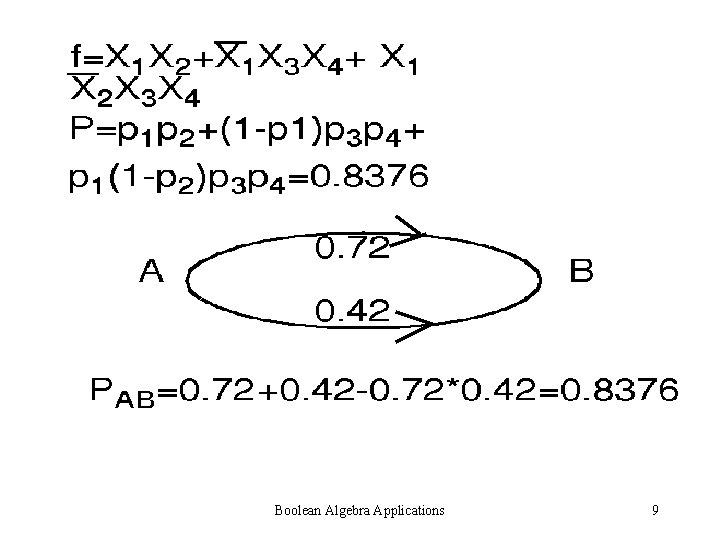
Boolean Algebra Applications 9
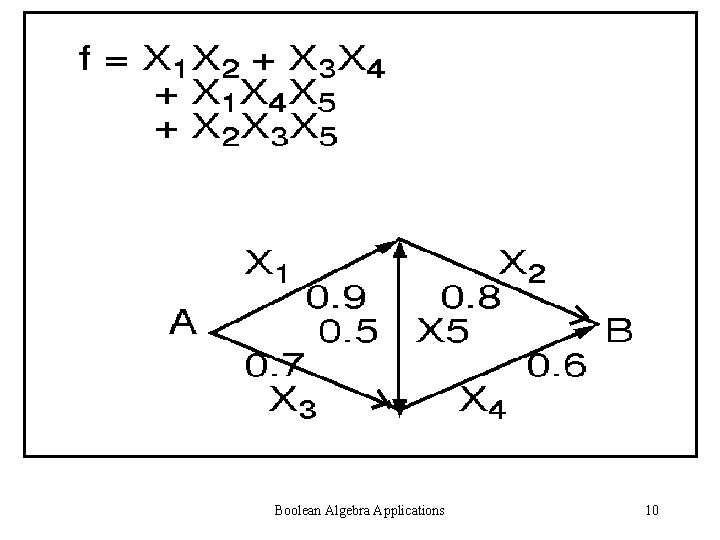
Boolean Algebra Applications 10
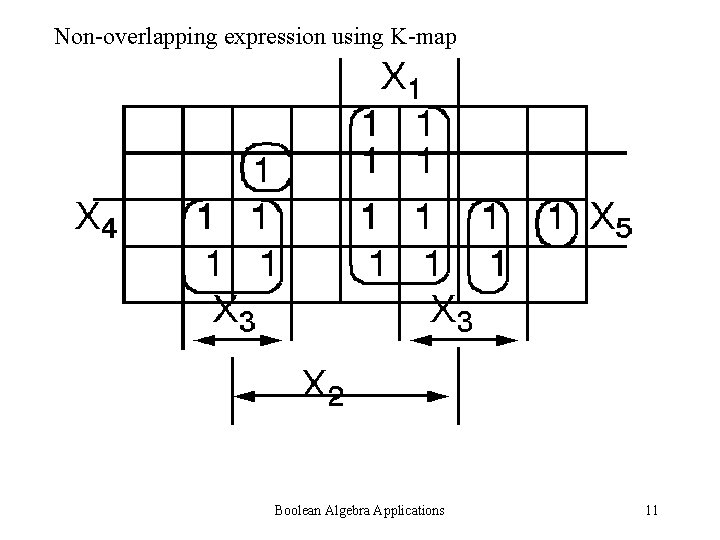
Non-overlapping expression using K-map Boolean Algebra Applications 11

Boolean Algebra Applications 12

F & M METHOD L. Fratta & V. Montanari Discuss boolean algebra approach for determining terminal reliability Boolean Algebra Applications 13

Algorithm • Determine all paths • Write down the corresponding boolean expression • Determine non-overlapping simplification • Transform into mathematical expression • Substitute reliability values Boolean Algebra Applications 14

Algorithm Step 1: Let S be the set of all simple paths between the terminal nodes. Construct a Boolean sum of products f, where each product corresponds to a path S and whose factors are exactly the noncomplemented variables corresponding to the arcs in the path Boolean Algebra Applications 15

Algorithm Let P = 0 Step 2: If f has no terms, stop Step 3: Select any term A of f Step 4: Let A’ be the arithmetic monomial which is equivalent to A Boolean Algebra Applications 16

Algorithm Let P = P + A’ Step 5: Let A’. f --> f and reduce f to a sum of products. Go to step 2. Boolean Algebra Applications 17
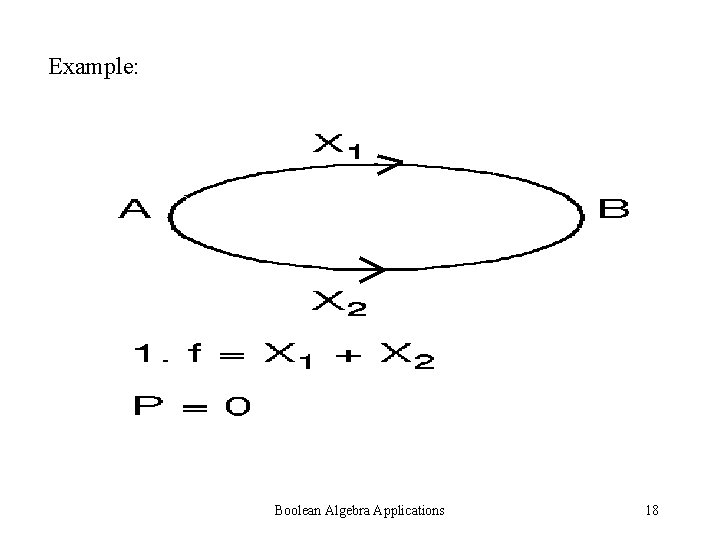
Example: Boolean Algebra Applications 18

Boolean Algebra Applications 19
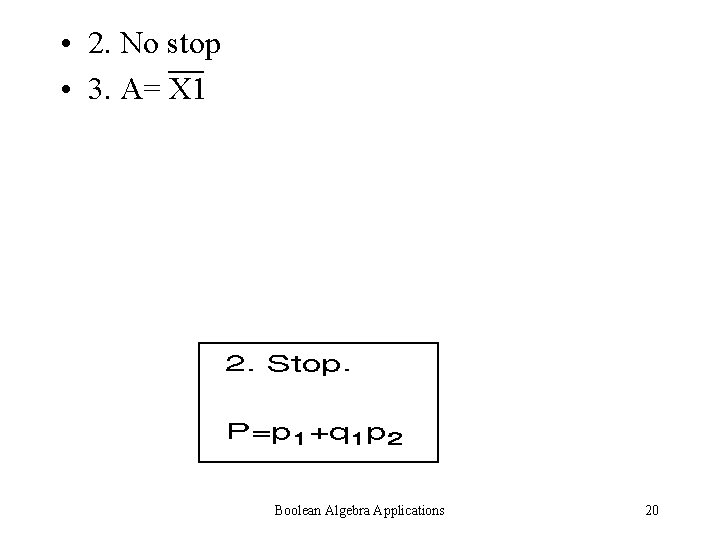
• 2. No stop • 3. A= X 1 Boolean Algebra Applications 20
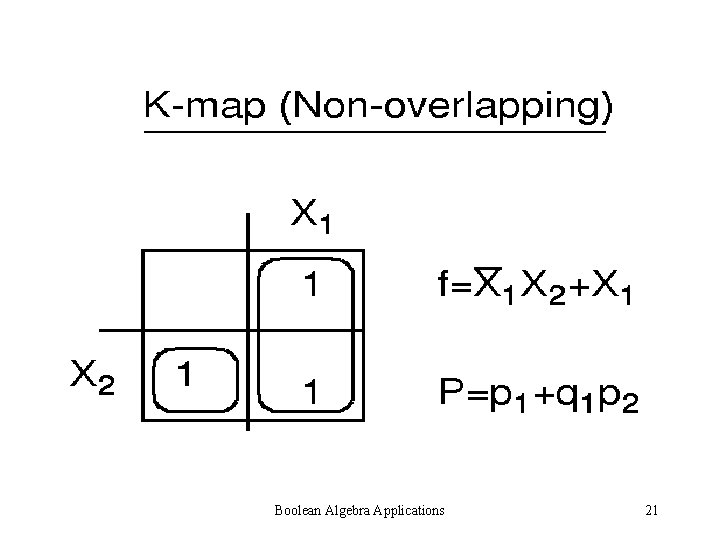
Boolean Algebra Applications 21
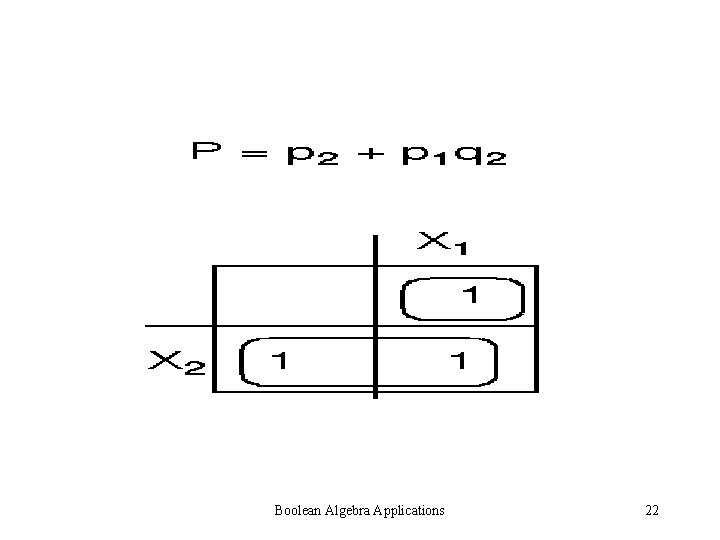
Boolean Algebra Applications 22
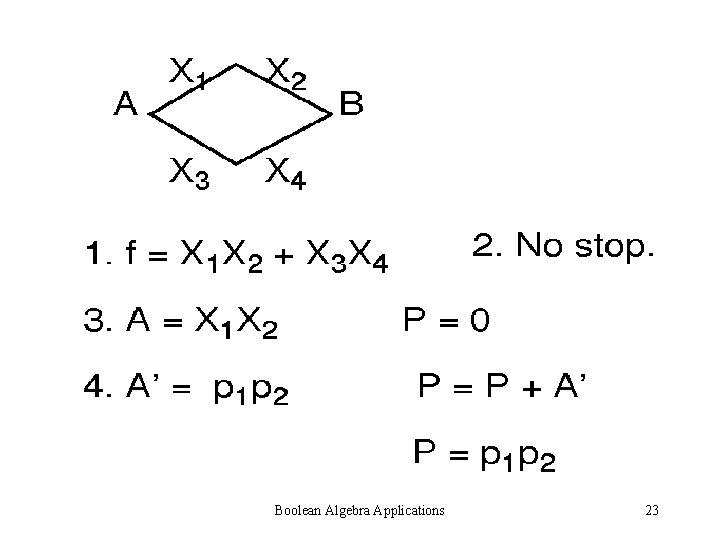
Boolean Algebra Applications 23

Boolean Algebra Applications 24

Boolean Algebra Applications 25

Boolean Algebra Applications 26

K- Map Method Boolean Algebra Applications 27
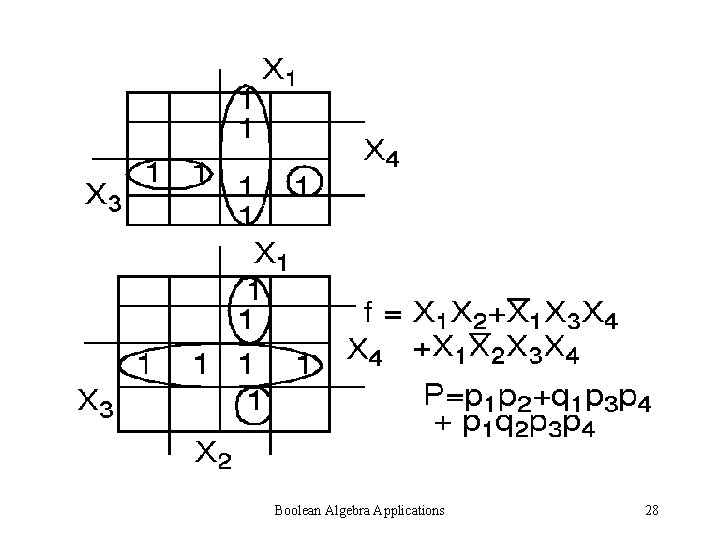
Boolean Algebra Applications 28

Boolean Algebra Applications 29
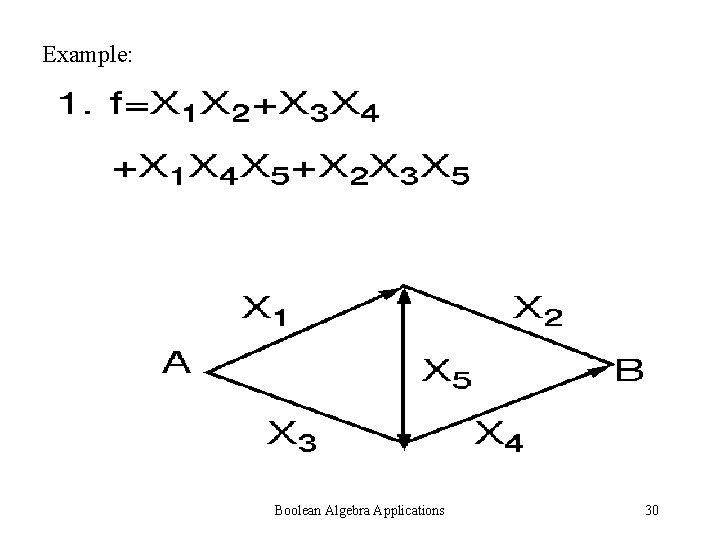
Example: Boolean Algebra Applications 30

Boolean Algebra Applications 31

Boolean Algebra Applications 32

Boolean Algebra Applications 33

Boolean Algebra Applications 34

Boolean Algebra Applications 35

Boolean Algebra Applications 36

Boolean Algebra Applications 37

Boolean Algebra Applications 38

Boolean Algebra Applications 39
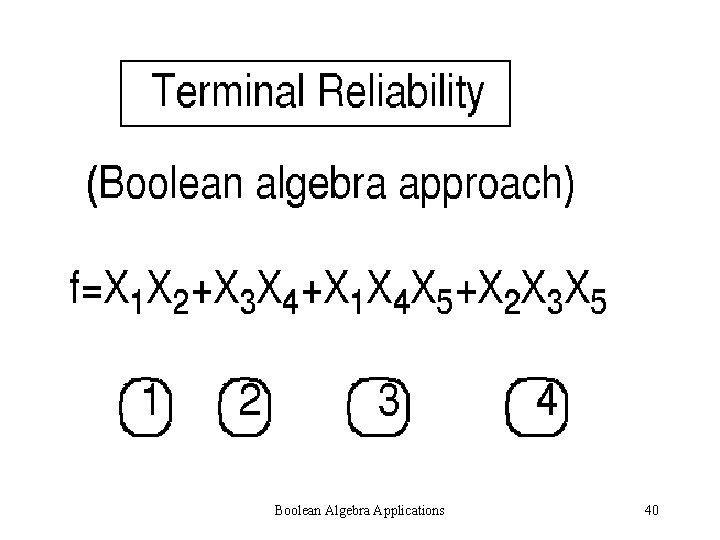
Boolean Algebra Applications 40

X 1 X 2 Boolean Algebra Applications 41

X 3 X 4 Boolean Algebra Applications 42

X 1 X 4 X 5 Boolean Algebra Applications 43

X 2 X 3 X 5 Boolean Algebra Applications 44
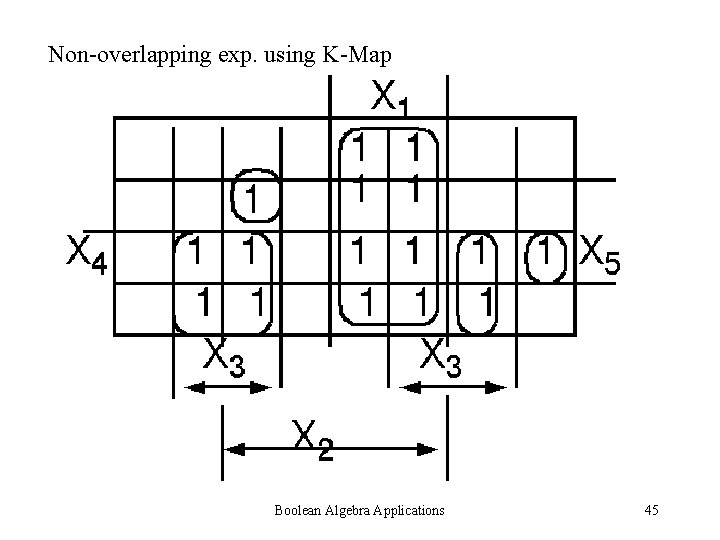
Non-overlapping exp. using K-Map Boolean Algebra Applications 45

Boolean Algebra Applications 46
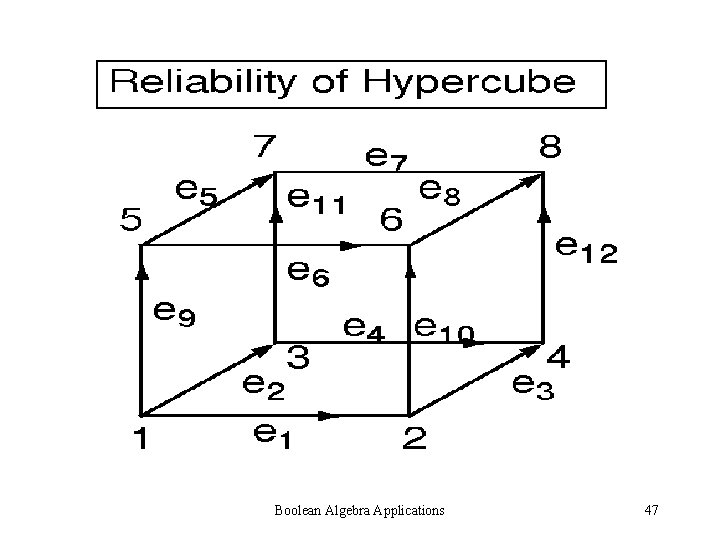
Boolean Algebra Applications 47

Boolean Algebra Applications 48
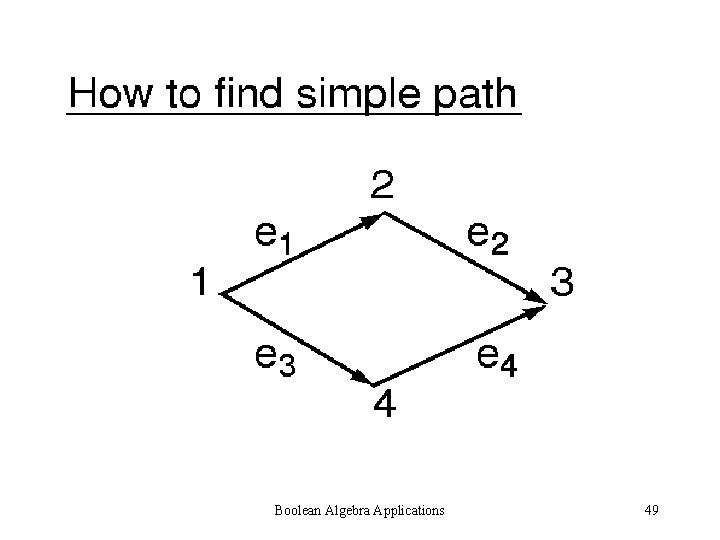
Boolean Algebra Applications 49
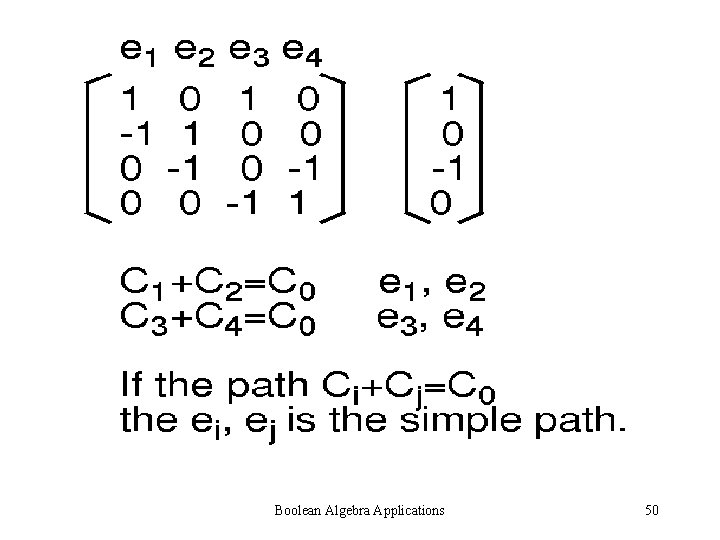
Boolean Algebra Applications 50
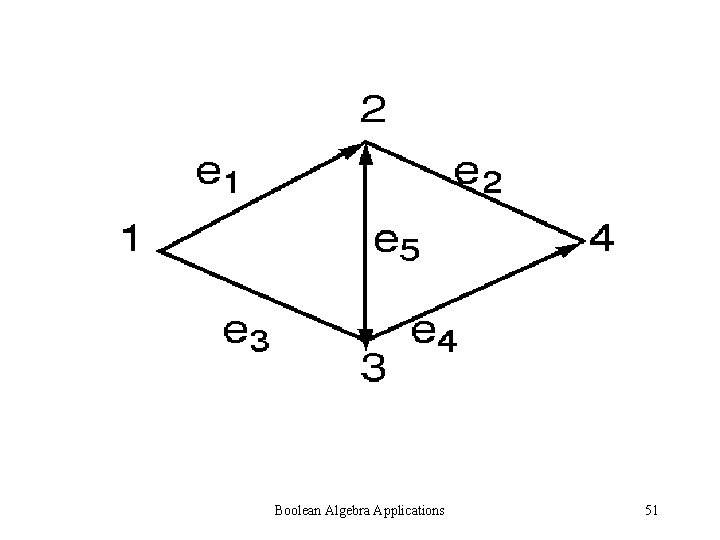
Boolean Algebra Applications 51
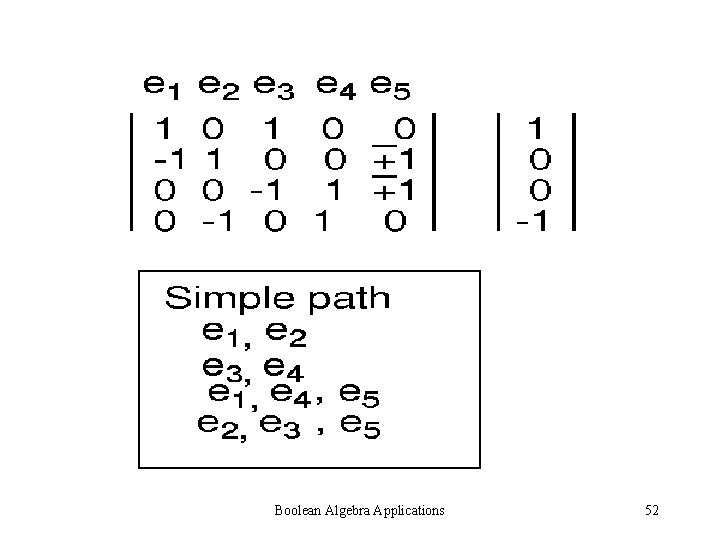
Boolean Algebra Applications 52
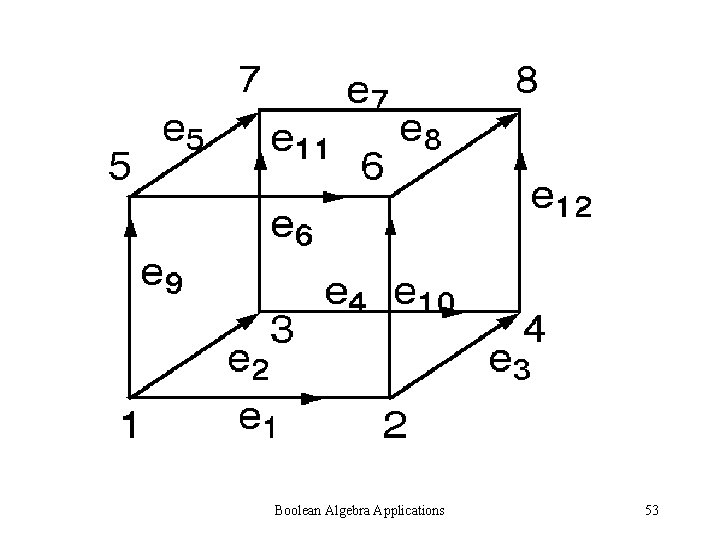
Boolean Algebra Applications 53
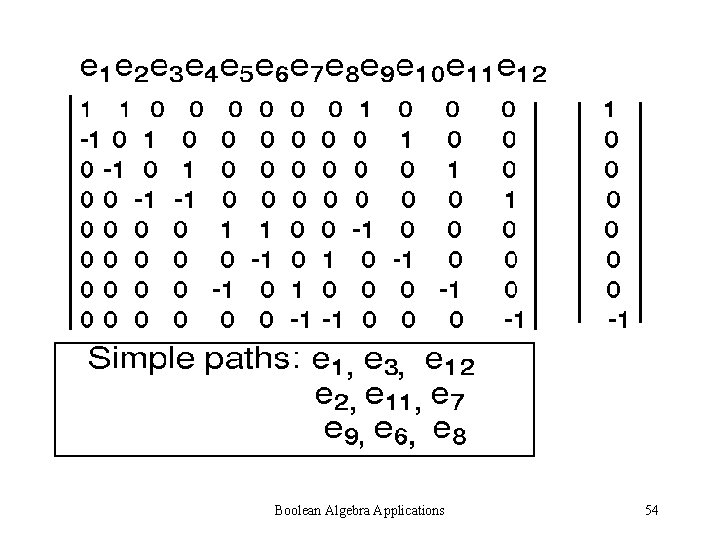
Boolean Algebra Applications 54
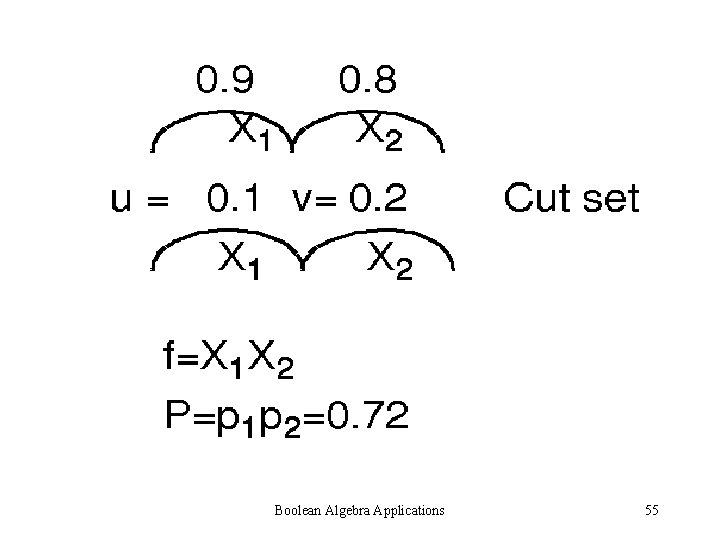
Boolean Algebra Applications 55

Boolean Algebra Applications 56
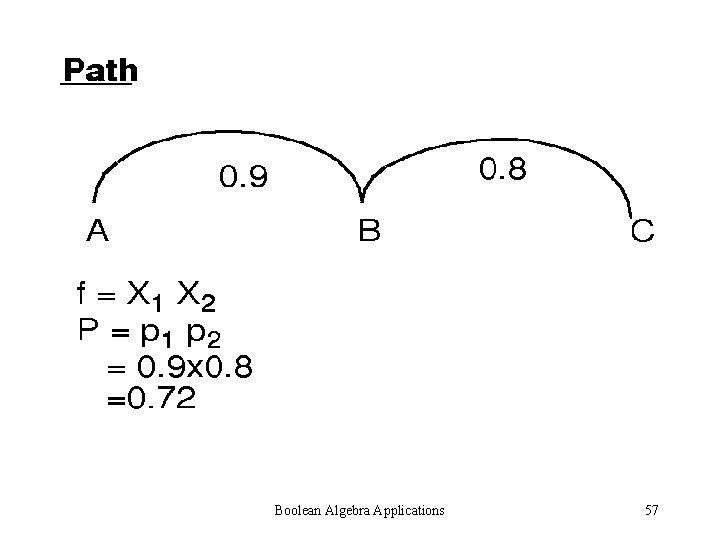
Boolean Algebra Applications 57
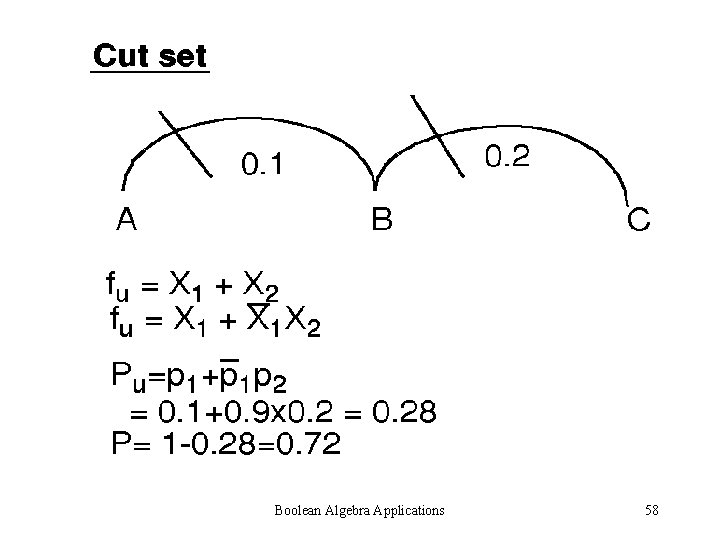
Boolean Algebra Applications 58
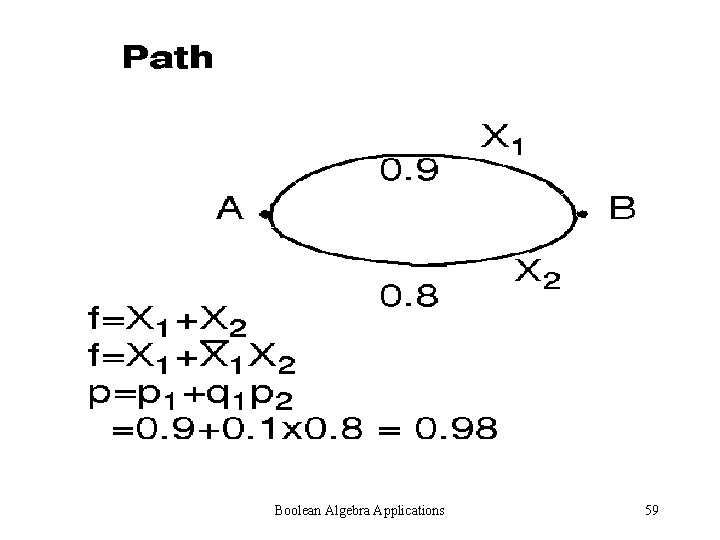
Boolean Algebra Applications 59
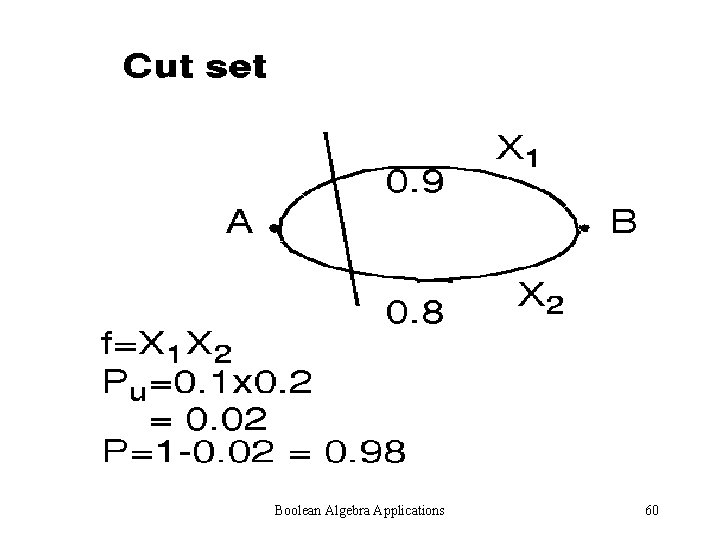
Boolean Algebra Applications 60

Questions ? Boolean Algebra Applications 61
- Slides: 61