Logic Chapter 2 Proposition Proposition can be defined

Logic Chapter 2

Proposition • "Proposition" can be defined as a declarative statement having a specific truth-value, true or false. • Examples: ü 2 is a odd number. ü 4 is a perfect square. • The above statements are propositions as they have precise truth values. Their truth values are false and true, respectively.

Connective • "Connective": Two or more propositions can be combined together to make compound propositions with the help of logical connectives. • Examples: ü 2 is an odd number AND 4 is a perfect square. ü 2 is an odd number OR 4 is a perfect square. • Above two propositions can be used to make a compound proposition using any of the logical connectives. • Their truth vales are false and true respectively. For the first compound proposition to be true both the propositions have to be true as the connective is AND. • As OR is the connective for the second one if either of the propositions is true the truth value of the compound proposition is true.

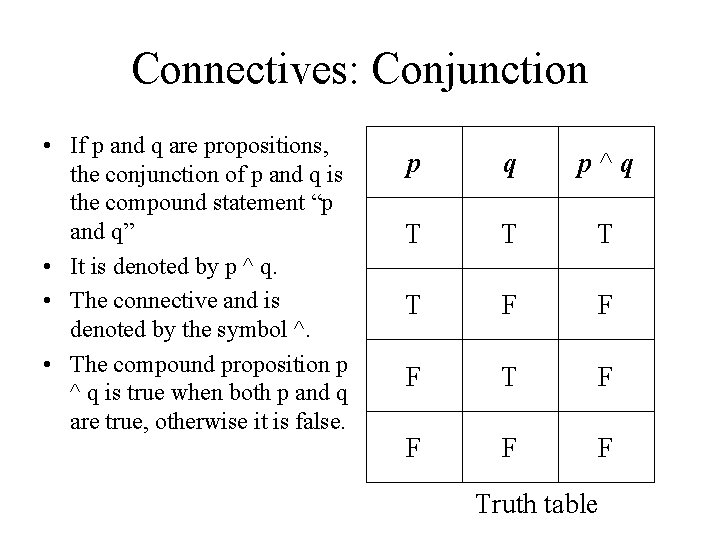
Connectives: Conjunction • If p and q are propositions, the conjunction of p and q is the compound statement “p and q” • It is denoted by p ^ q. • The connective and is denoted by the symbol ^. • The compound proposition p ^ q is true when both p and q are true, otherwise it is false. p q p ^ q T T F F F Truth table

Connectives: Disjunction • If p and q are propositions, the disjunction of p and q is the compound statement “p or q” • It is denoted by p v q. • The connective or is denoted by the symbol v. • The compound proposition p v q is true if at least one of p or q is true, it is false when both p and q are false. p q p v q T T F F F Truth table

Negation • If p is a proposition, the negation of p is the statement not p. • It is denoted by ~p or ¬p. p ~ p or ¬p T F F T

Conditional Statement • If p and q are statements, the compound statement ‘if p then q’ (denoted by p => q) is called a conditional statement / implication. • The statement p is called hypothesis. • The statement q is called the consequent /conclusion. • The connective if …then is denoted by the symbol =>.

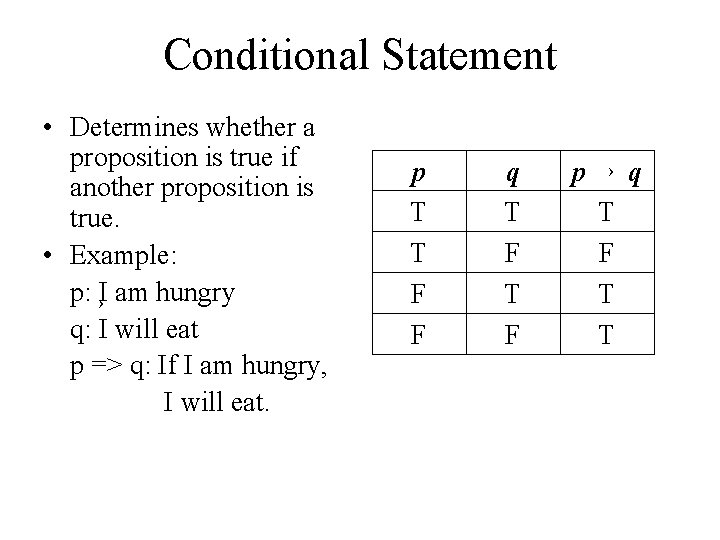
Conditional Statement • Determines whether a proposition is true if another proposition is true. • Example: p: I am hungry q: I will eat p => q: If I am hungry, I will eat. p T T F F q T F p q T F T T

Conditional Statement • p -> q is also expressed in a number of different (but equivalent) ways in English. • For example, the following are all different ways of saying "if p then q". ü "p only if q" , ü "if not q then not p" , ü "p is sufficient for q" , ü "q is necessary for p", ü "q is a necessity/consequence of p" and ü "q whenever p"

Converse, Contrapositive, and Inverse • If p =>q is an implication, then √ the converse of p => is the implication q => p. √ the contrapositive of p => q is the implication ~q => ~p. ü the inverse of p => q is is the implication ~p => ~q. • Examples: p: I am elected q: I will lower taxes p => q: If I am elected, then I will lower taxes. Converse: q => p: I will lower taxes if I am elected. Contrapositive: ~q => ~p: I will not lower taxes if I am not elected. Inverse: ~p => ~q: If I am not elected, then I will not lower the taxes.

Converse, Contrapositive, and Inverse Q What are the contrapositive, the converse, and the inverse of the implication “The home team wins whenever it is raining”? S “q whenever p” is one of the ways to express the implication p => q, the original statement can be written as ”If it is raining, then home team wins”. ü Contrapositive: If the home team does not win, then it is not raining. ü Converse: If the home team wins, then it is raining. ü Inverse: If it is not raining, then the home team does not win.

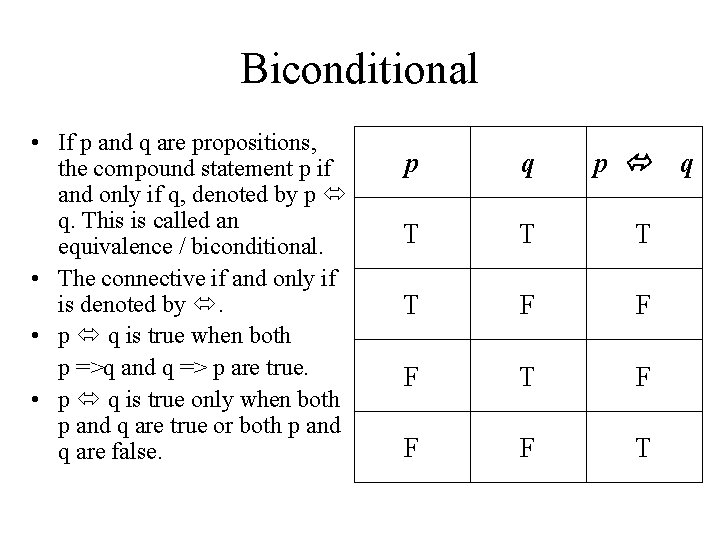
Biconditional • If p and q are propositions, the compound statement p if and only if q, denoted by p q. This is called an equivalence / biconditional. • The connective if and only if is denoted by . • p q is true when both p =>q and q => p are true. • p q is true only when both p and q are true or both p and q are false. p q p T T F F F T q

Biconditional • There are some other common ways to express p q: ü “p is necessary and sufficient for q” ü “if p then q, and conversely” ü “p iff q” (iff is the abbreviation for ‘if and only if”) • Note: p q has exactly the same truth value as (p => q) ^ (q => p).

Biconditional • Example 1: p: You can take the flight, q: You buy a ticket. p q : You can take the flight if and only if you buy a ticket. • Example 2: p: You can have dessert, q: You finish your meal. p q : You can have dessert if and only if you finish your meal.

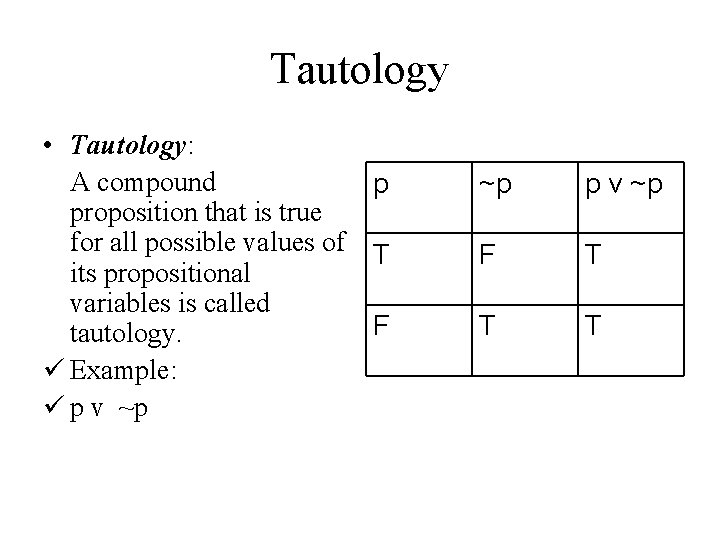
Tautology • Tautology: A compound p proposition that is true for all possible values of T its propositional variables is called F tautology. ü Example: ü p v ~p F T T T

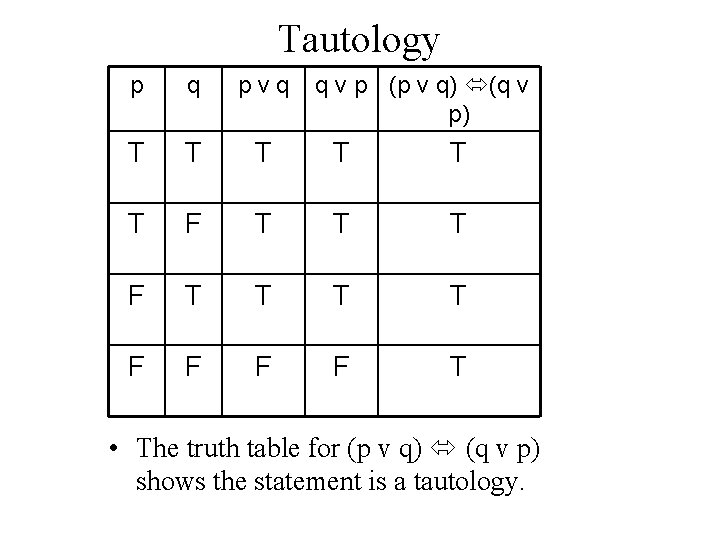
Tautology q v p (p v q) (q v p) p q pvq T T T F T T T T F F T • The truth table for (p v q) (q v p) shows the statement is a tautology.

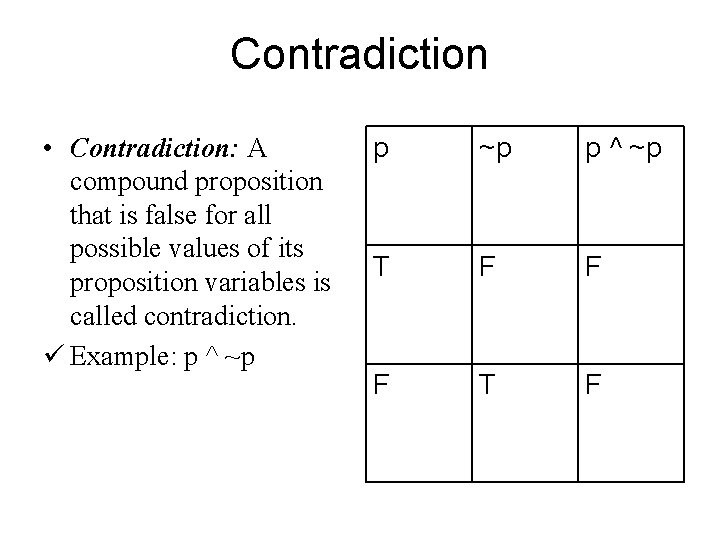
Contradiction • Contradiction: A compound proposition that is false for all possible values of its proposition variables is called contradiction. ü Example: p ^ ~p T F F F T F

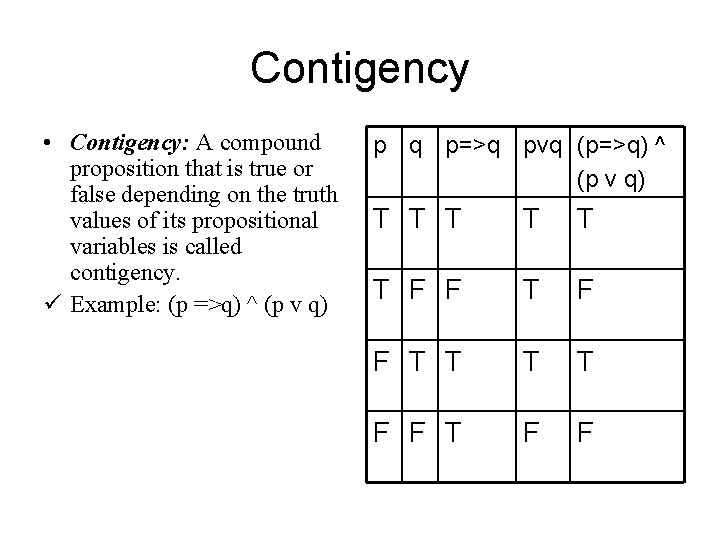
Contigency • Contigency: A compound proposition that is true or false depending on the truth values of its propositional variables is called contigency. ü Example: (p =>q) ^ (p v q) p q p=>q pvq (p=>q) ^ (p v q) T T T F F T T T T F F

Quantifiers • Set is defined as A = {x | P(x)} where p(x) is predicate/propositional function • Quantification: universal & existential quantifications • The universal quantification of P(x) is the proposition “P(x) is true for all values of x in the universe of discourse”. • The notation Vx P(x) denotes the universal quantification of P(x). V is called the universal quantifier

Universal Quantifier Q Let P(x) be the statement “x+1>x”. What is the truth value of the quantification Vx P(x), where the universe of discourse consists of all real numbers? S Since P(x) is true for all real numbers x, the quantification Vx P(x) is true. Q Let Q(x) be the statement “x < 2”. What is the truth value of the quantification Vx Q(x), where the universe of discourse consists of all real numbers? S Q(x) is not true for all real numbers x, since for instance Q(3) is false. Thus the quantification Vx Q(x) is false.

Existential Quantifier • With existential quantification, we form a proposition that is true if and only if P(x) is true for at least one value of x in the universe of discourse. • The existential quantification P(x) is the proposition “There exists an element x in the universe of discourse such that P(x) is true” • We can use the notation Ξ x P(x) for existential quantification of P(x). Ξ is called the existential quantifier.

Existential Quantifier Q Let P(x) be the statement “x>3”. What is the truth value of the quantification Ξ P(x), where the universe of discourse consists of all real numbers? S Since “x>3” is true – for instance, when x = 4 - the existential quantification of P(x), which is Ξ x P(x), is true. Q Let Q(x) be the statement “x = x + 1”. What is the truth value of the quantification Ξ x Q(x), where the universe of discourse consists of all real numbers? S Q(x) is false for all real numbers x, the existential quantification of Q(x), which is Ξ x Q(x), is false.