Boolean Algebra Supplementary material A Boolean algebra B

Boolean Algebra Supplementary material

A Boolean algebra • B is a boolean algebra means B is a set with elements in it a, b, …, 0, 1Є B and operators * (and), + (or) and ‘ (not) following the axioms • Closure: if a, b Є B then a+b Є B , a*b Є B and a’ Є B • Commutative: if a, b Є B then a+b=b+a and a*b=b*a • Distributive: if a, b, c Є B then a*(b+c)=a*b+a*c and a+(b*c) =(a+b)*(a+c) • Identitity elements: there are elements 0, 1 Є B such that 1*a=a and 0+a=a • Complementary Law: for aЄ B a+a’=1 and a*a’=0

Theorems (to prove) • • • Associative law. For a, b, c Є B a*(b*c)=(a*b)*c and a+(b+c)=(a+b)+c Idempotent property: for a Є B, a+a=a and a*a=a Identity elements act as null elements: For a Є B, a+1=1 and a*0=0 Involution: For a Є B, (a’)’ =a Absorption: for a, b Є B, a+(a*b)=a and a*(a+b)=a De. Morgan’s Laws: for a, b Є B, (a*b)’=a’+b’ and (a+b)’=a’*b’

Some sample proofs • a+a=a • Proof: • a=0+a – =a*a’+a – =a+a*a’ – (a+a)*(a+a’) – (a+a)*1 – a+a

More sample proofs • a+1=1 • Proof: • 1=a+a’ – – – =a+1*a’ =(a+1)*(a+a’) =(a+1)*1 1*(a+1) a+1

Sample proofs continued • a*0=0 • Proof • a*0=0+a*0 – a*a’+a*0 – a*(a’+0) – a*(0+a’) – a*a’ – 0

Absorption: proof of one of them • a+a*b=a • Proof • a+a*b=1*a+a*b – – – =a*1+a*b =a*(1+b) =a*1 =1*a =a

De. Morgan • • (a*b)’=a’+b’ proof: This is a complicated proof that requires two parts. Notice that theorem seems to say that if you negate the parenthesized expression on the LHS you wind up with the RHS, sort of like x’=z, (which is something like saying the negation of x is z). We might use this idea. First, x and z should behave like “opposites”, that is, if we take x and + it with z we should get 1 and x*z should be 0. • Also, we’ll need to show that if two booleans behave this way, then they are “opposites”, that is, if x+z=1 and x*z=0 then x’=z

De. Morgan continued • Show if x+z=1 and x*z=0 then x’=z. • (proof) • x’ =1*x’ – – – – =(x+z)*x’ =x’*(x+z) =x’*x+x’*z =0+x’*z x*z+x’*z z*(x+x’) z

Completeness • A set of operators is complete iff all switching functions of n variables can be written using only that set. • The set {*, +, ’} is complete. • DNF==SOP and CNF==POS are canonical representations of switching functions. They use the idea of Duals – one is the dual of the other.

Generating switching functions using DNF • Start with the table for f • For each row in f which has a value of 1, generate one term in the DNF and put an ‘or’ symbol (+) between each term. • Generate the terms as follows, if the variable v is a 0 in this row, put v’ into the product, if v is a 1 in this row, put v in the product.
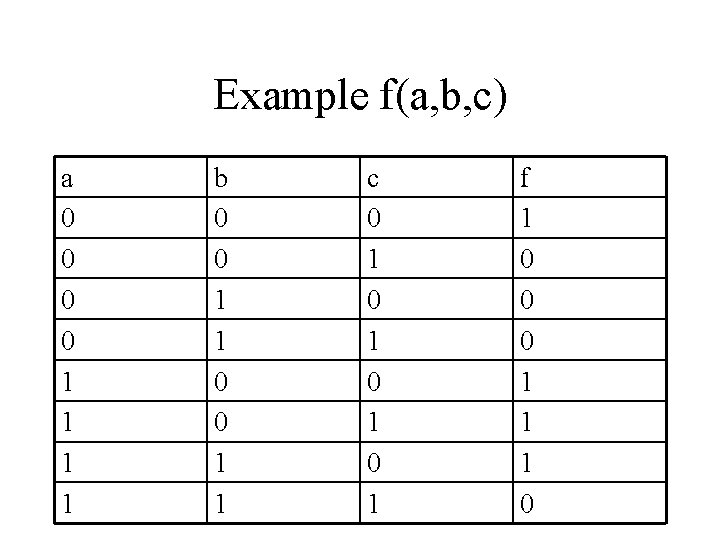
Example f(a, b, c) a 0 0 1 1 b 0 0 1 1 c 0 1 0 1 f 1 0 0 0 1 1 1 0

DNF (or POS) for f • f’s DNF has 4 terms, corresponding to the numerical values – rows - 0, 4, 5, 6 • f=a’*b’*c’+a*b’*c+a*b*c’

CNF • To get the cnf use the dual concept. Generate a term (a sum, though) for each 0 valued row of f. For variable v a 0 add v to the sum, if v is a 1 add v’ to the sum. Conjunct all terms.
- Slides: 14