1 4 Basic Rules of Algebra Terms terms

1. 4 Basic Rules of Algebra

Terms terms – parts of an algebraic expression separated by addition (or subtraction) signs Ex: 2 x + 5 2 terms 2 x (2 times x) 2 is the “coefficient” or # part 5 is a “constant” (no variable)

Properties commutative property of addition a+b=b+a Ex: 2 + 3 = 3 + 2 commutative property of multiplication a∙b=b∙a Ex: 2 ∙ 3 = 3 ∙ 2 (we can change the order when we add or mult. without changing the result)

associative property of addition (a + b) + c = a + (b + c) Ex: (2 + 3) + 4 = 2 + (3 + 4) associative property of multiplication (a ∙ b) ∙ c = a ∙ (b ∙ c) Ex: (2 ∙ 3) ∙ 4 = 2 ∙ (3 ∙ 4) 6 ∙ 4 = 2 ∙ 12 24 = 24 (we can change the grouping of #s when we add or mult. w/o changing the result)
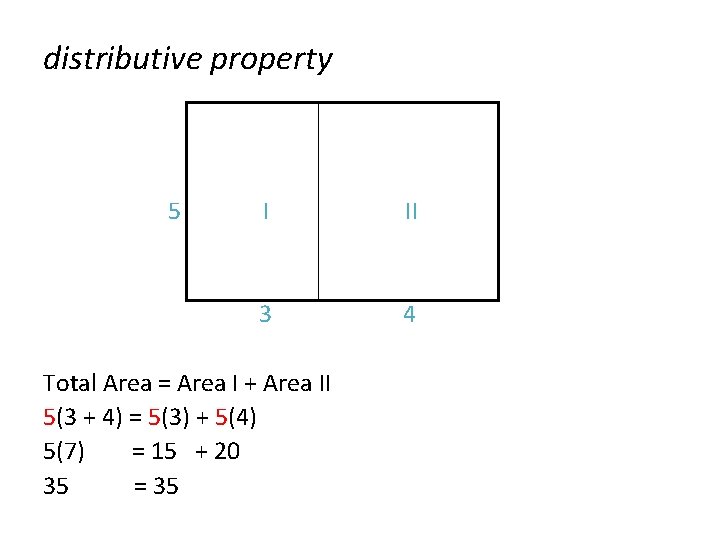
distributive property 5 I II 3 4 Total Area = Area I + Area II 5(3 + 4) = 5(3) + 5(4) 5(7) = 15 + 20 35 = 35

distributive property a(b + c) = ab + ac a(b – c) = ab – ac Ex: 3(r + 2) (2 x + 7)4 = 3(r) + 3(2) = 3 r + 6 = 4(2 x) + 4(7) = 8 x + 28
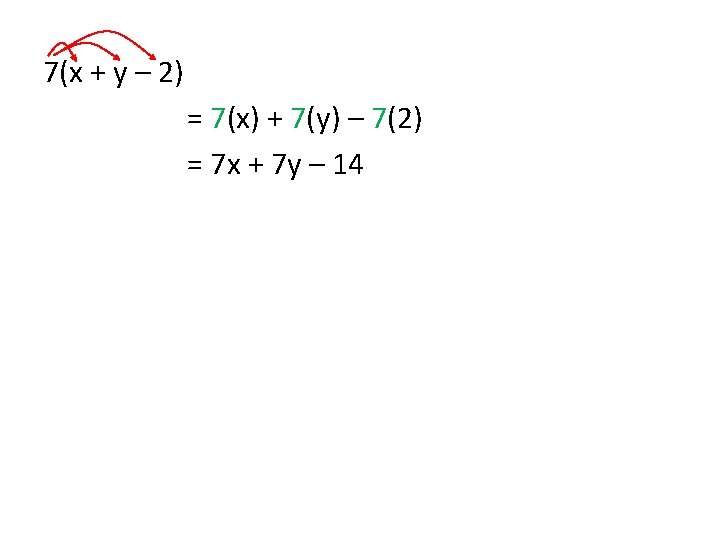

Simplifying an Algebraic Expression like (or similar) terms – 2 or more terms with the same variables raised to the same powers Ex: terms 3 x, 4 x 2 a 2 b, -7 a 2 b ½x 2 y, 13 xy 2 5, 8 m, 12 m like terms?

Ex: terms 3 x, 4 x 2 a 2 b, -7 a 2 b ½x 2 y, 13 xy 2 5, 8 m, 12 m like terms? yes no no

simplify – reduce the # of terms in an expression Ex: Simplify by combining like terms (a) 5 x + 2 x = (5 + 2)x = 7 x (b) 13 y – 7 y = (13 – 7)y = 6 y • to combine like terms, just add/sub. the coefficients • If there are ( ), use the distributive property first
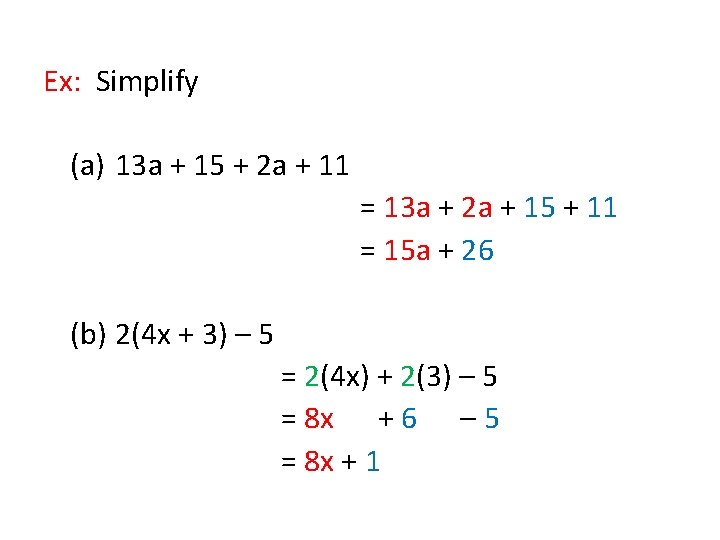
Ex: Simplify (a) 13 a + 15 + 2 a + 11 = 13 a + 2 a + 15 + 11 = 15 a + 26 (b) 2(4 x + 3) – 5 = 2(4 x) + 2(3) – 5 = 8 x + 6 – 5 = 8 x + 1
- Slides: 11