2016 2017 Algebra 2 Midterm Exam Review Solutions

2016 -2017 Algebra 2 Midterm Exam Review Solutions

Use the Distributive Property. Collect like terms.

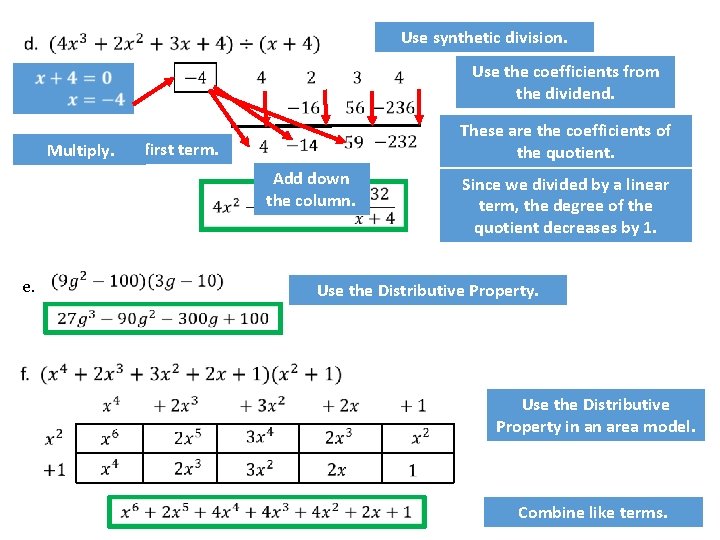
Use synthetic division. Use the coefficients from the dividend. Bring Multiply. down the first term. Multiply. These are the coefficients of the quotient. Add down the column. e. Since we divided by a linear term, the degree of the quotient decreases by 1. Use the Distributive Property. Use the Distributive Property in an area model. Combine like terms.

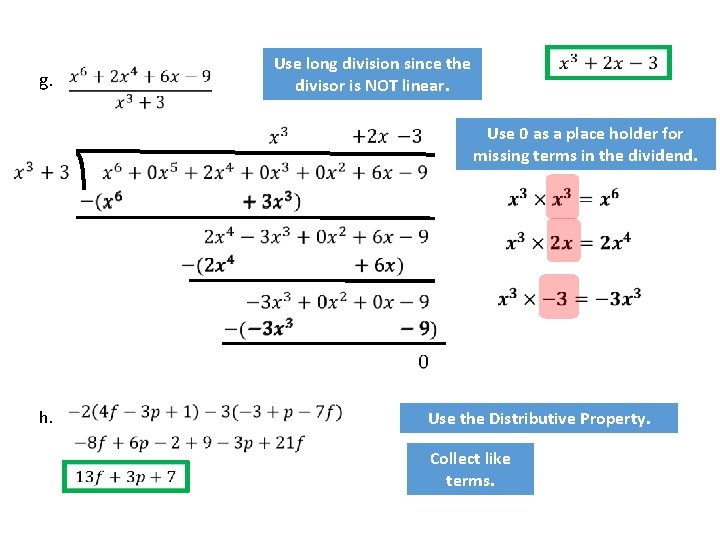
Use long division since the divisor is NOT linear. g. Use 0 as a place holder for missing terms in the dividend. h. Use the Distributive Property. Collect like terms.

Interchange x and y. Not Invertible because the inverse would not be a function. Solve for y. c. d. Interchange x and y. Solve for y. Interchange x and y. Solve for y.

Not Invertible because the inverse would not be a function. Interchange x and y. Solve for y. Move all y’s to one side of the equal sign. Factor.

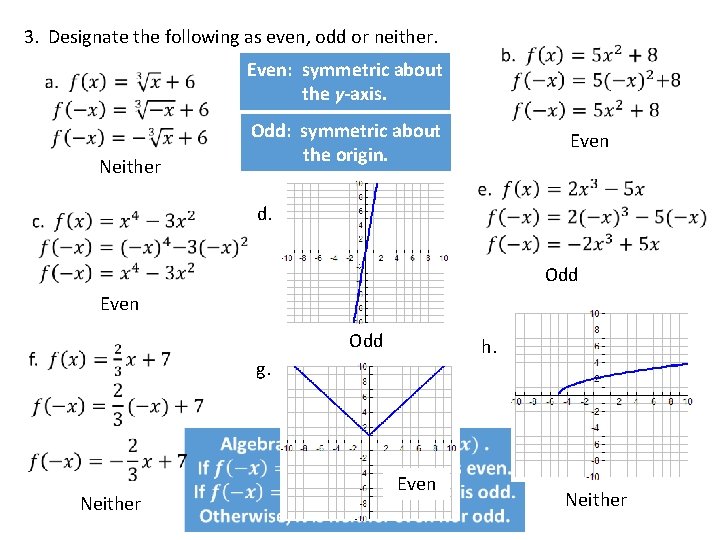
3. Designate the following as even, odd or neither. Even: symmetric about the y-axis. Odd: symmetric about the origin. Neither Even d. Odd Even Odd h. g. Neither Even Neither

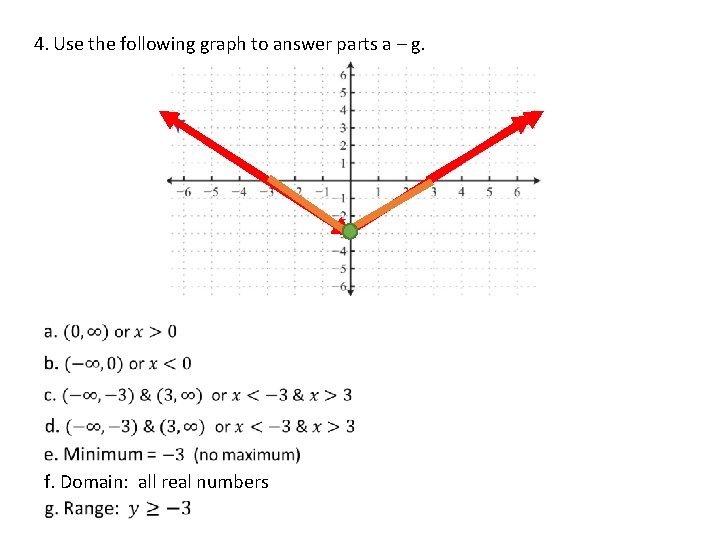
4. Use the following graph to answer parts a – g. f. Domain: all real numbers

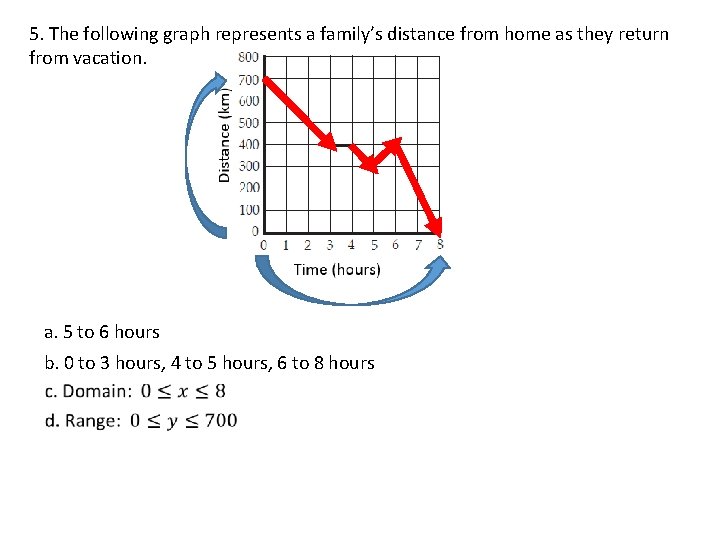
5. The following graph represents a family’s distance from home as they return from vacation. a. 5 to 6 hours b. 0 to 3 hours, 4 to 5 hours, 6 to 8 hours

The vertical compression results in this equation: Adding a translation 5 units to the right results in this equation: Adding a translation 4 units down results in this equation:

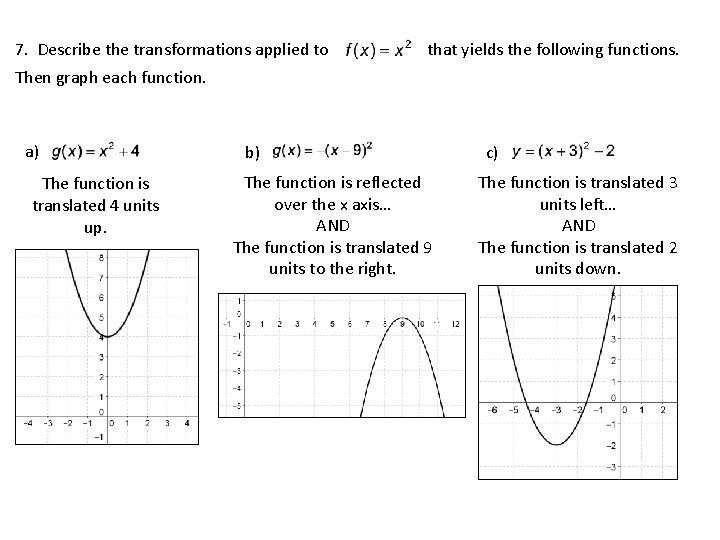
7. Describe the transformations applied to that yields the following functions. Then graph each function. a) The function is translated 4 units up. b) The function is reflected over the x axis… AND The function is translated 9 units to the right. c) The function is translated 3 units left… AND The function is translated 2 units down.

Take the square root of both sides of the equation Subtract.

slope: There is an additional $25 cost for each additional person attending prom. y-intercept: There is a $110 flat fee in the cost of the prom. (Perhaps the venue, music, etc. ) slope: Plants grow an additional 4. 2 cm each week. y-intercept: The plants started at a height of 12 cm.

10. Solve the following systems of equations. This is one method. a. Subtract y from both sides of the second equation. 0 Add the 2 equations together. Divide both sides of the equation by 7. Substitute x = 2 into one of the equations to solve for y. 0

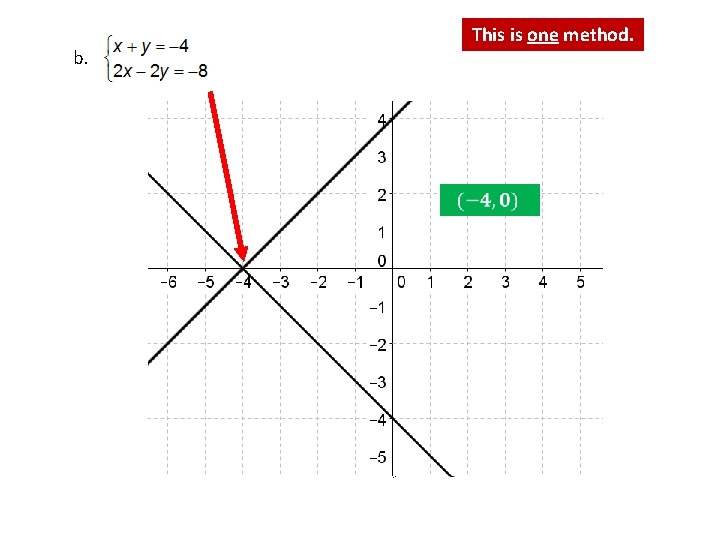
This is one method. b.

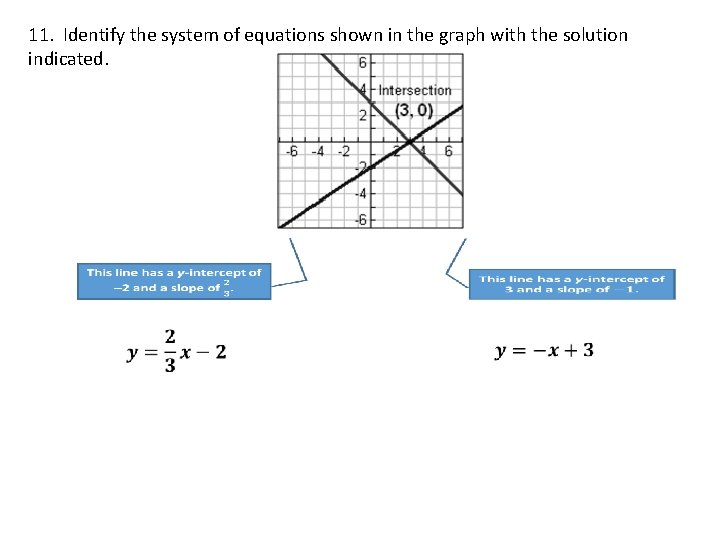
11. Identify the system of equations shown in the graph with the solution indicated.

12. At a bookstore, used hardcover books sell for $8 each and used paperback books sell for $2 each. Sheila purchased 36 used books and spent $144. Write a system of equations that can be used to find how many hardcover and paperback books Sheila bought. Then state how many paperback books Sheila actually purchased Write a system of equations to model the situation. Let’s eliminate h since we are looking for p. Add the 2 equations together. Let h = # hardcover books and p = # of paperback books. Mulitply the first equation by – 8. Divide both sides of the equation by – 6. 24 paperbacks

13. A group of 52 people attended a ball game. There were three times as many children as adults in the group. Set up a system of equations that represents the numbers of adults and children who attended the game and solve the system to find the number of children who were in the group Write a system of equations to model the situation. Let a = # adults at the game and c = # of children at the game. Combine like terms. Divide both sides of the equation by 4. Substitute a = 13 into one of the equations to find c. 39 children

14. Let g = # of pounds of gummy worms c = # of pounds of candy corn s = # of pounds of sourballs Let m = # of mums o = # of orchids r = # of roses

15. Marco is buying hamburgers and hot dogs for a party and only has $40 to spend. Hamburgers cost $6. 49 per pound. Hot dogs cost $4. 99 per pound and Marco needs at least 5 pounds of hot dogs. Write a system of inequalities to represent this situation. Let h = # hamburgers and d = # of hot dogs. 16. The boys and girls golf teams are trying to raise $750 for an out-of-county tournament. The boys team is selling candy bars for $2 each. The girls team is selling candles for $4 each. The girls need to sell at least 100 candles to clear out already purchased inventory. Write a system of inequalities to represent this situation. Let b = # of candy bars the boys sell and g = # of candles the girls sell.

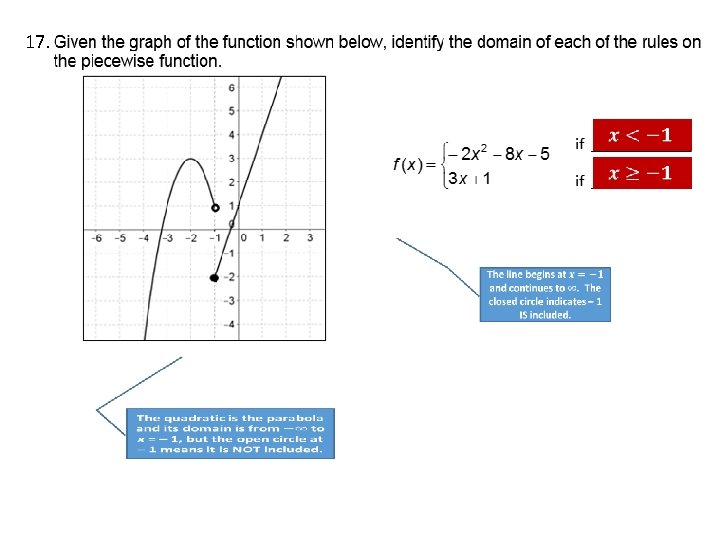
17.

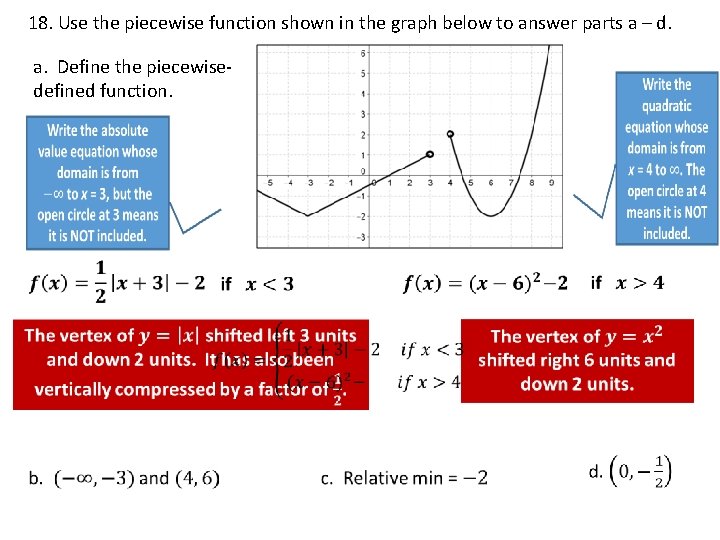
18. Use the piecewise function shown in the graph below to answer parts a – d. a. Define the piecewisedefined function.

19. The local pet store charges for grooming according to your pet’s weight. If your pet is 10 pounds or less, they charge $30. If your pet is between 10 and 30 pounds, they charge $35. If your pet is 30 pounds or more, they charge $40, plus an additional $2 for each pound over 30. a. How much does it cost to groom a pet who weighs 47 pounds? Let’s define the function where x = # pounds a pet weighs. Since 47 > 30, we use the last piece of the function. b. Over what interval is this piecewise-defined function increasing? c. What does the y-intercept of this graph mean in context? A pet that weighs 0 pounds (or no pet) costs $0 to groom.

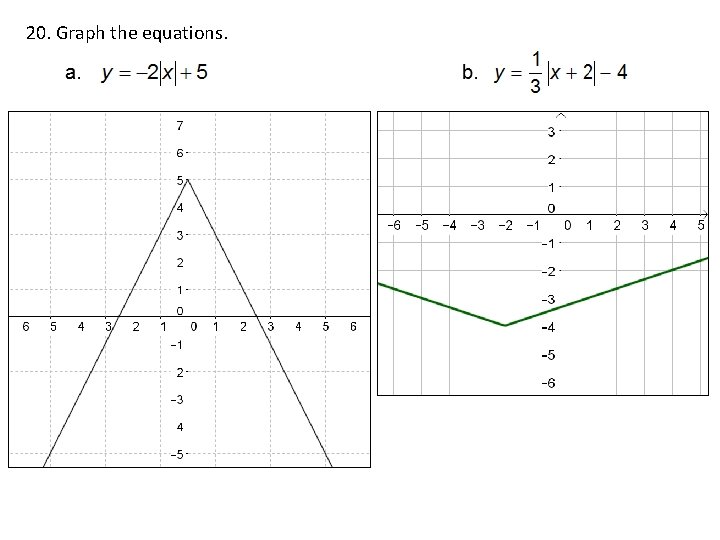
20. Graph the equations.

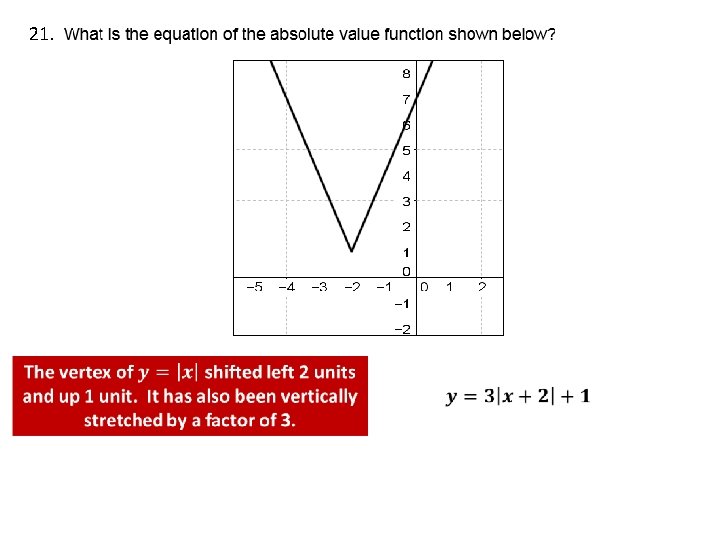
21.

22. Fill in the missing properties for the solution of the equation given below. [5 x was subtracted from both sides. This is an example of the…] Subtraction Property of Equality. [The left side of the equation was factored. This is an example of …] Factor. [Each factor is set equal to zero. This is an example of the…] Zero Product Property. [Each factor experiences the same process. A number was added to each side of both equations. This is an example of the…] Addition Property of Equality. [The left equation is multiplied by ½ or is divided by 2. Either (but not both) are correct. This is an example of either the…] Multiplication Property of Equality OR Division Property of Equality (but NOT both).

23. Select all of the following justifications NOT used in the solution of the equation shown below. 75 was added to or – 75 was subtracted from both sides of the equation. This is either the Addition Property of Equality OR the Subtraction Property of Equality. But it cannot be both. Square root both sides of the equation. Simplify the radical. Answers may vary: a or b (but not both), c, d or e (but not both), f, g, i

24. When the ball hits the ground, the height is 0. Since time cannot be negative, the ball hit the ground after 5 seconds.

a. What expression can be used to find the length of one side? Factor. b. What is the length of the rug? (Answers may vary) The length of the rug must be greater than 8 feet.

26. To identify the zeros, set y equal to 0 and factor. Identify two numbers that. Factor multiply – 60 outto the GCF and addcolumns to – 11. and up the Multiply across – 15 andthe +4 rows. and

To identify the zeros, set y equal to 0 and factor. Identify numbers Factor two the GCF up that – 15 themultiply columnsto and add 2. across theto rows Multiply +5 and – 3 and

To identify the zeros, set y equal to 0 and factor. Factor out the GCF. Identify two Factor thenumbers GCF up that multiply toand 30 the columns and addthe to 11. across rows Multiply +5 and +6 and

Simplify the radicals. Distribute the negative. Combine like terms. Simplify the radicals. Combine like terms.

Distribute the negative. Use the Distributive Property Distribute the negative.

Subtract 49 from both sides of the equation. Divide both sides of the equation by 25. Use square roots.

This equation is not factorable, so we can use the Quadratic Formula. a = 1 b = 2 c = -2 Substitute the values for a, b, and c into the formula. Simplify. Simplify the numerator and denominator using a factor of 2.

Use completing the square and square roots to solve. Take half of the x coefficient To keep the equation add 9 to square it. balanced, Add this and number to create a both sides of the equation. perfect square trinomial. Factor the perfect square trinomial and combine like terms. Square root both sides of the equation. Add 3 to both sides of the equation.

This equation is not factorable, so we can use the Quadratic Formula. a = 3 b = 3 c = 2 Substitute the values for a, b, and c into the formula. Simplify.

Divide both sides of the equation by 5. Use square roots.

Set the equation equal to zero by subtracting 4 x from both sides of it. This equation is not factorable, so we can use the Quadratic Formula. a = 3 b = -4 c = 10 Substitute the values for a, b, and c into the formula. Simplify. Simplify the numerator and denominator using a factor of 2.

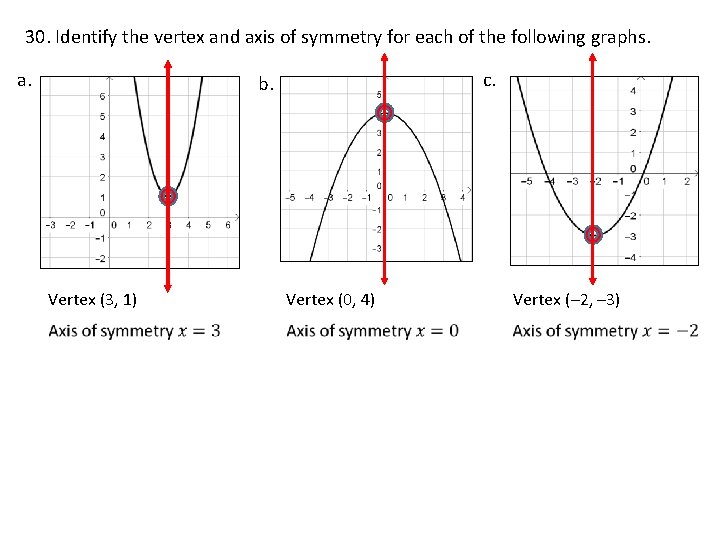
30. Identify the vertex and axis of symmetry for each of the following graphs. a. c. b. Vertex (3, 1) Vertex (0, 4) Vertex (– 2, – 3)

31. Since a = +1, the parabola opens up and has a minimum value. The minimum = 11 and occurs at the vertex (2, 11). Part b has a smaller minimum. The parabola opens up and has a minimum value. The minimum = 3 and occurs at the vertex (2, 3).

32. Which of the following functions has the largest maximum? a) To find the vertex, solve for c) b) Note the duplicated y values when x=0 and x=4 (and again at x=-2 & x=6). This shows the vertex of the parabola is at (2, -4). Plug in the x coordinate of ½ to find the y coordinate of the vertex. The above has a vertex at (-2, -1) and opens down. Since it opens down, it has a maximum. The maximum is at y = -1. The leading coefficient is negative, so this parabola opens down. The vertex is (. 5, -2. 75). The maximum is y= – 2. 75. Since the y values are decreasing on either side of the vertex, the parabola is opening down. Since it opens down, it has a maximum. The maximum is at y = -4. Comparing the maximum values from (a), (b), and (c), the function with the largest maximum is (b).

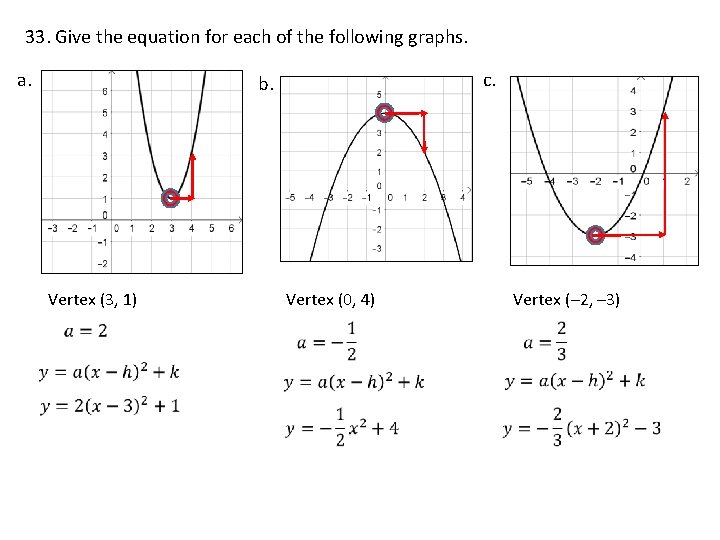
33. Give the equation for each of the following graphs. a. c. b. Vertex (3, 1) Vertex (0, 4) Vertex (– 2, – 3)

Use completing the square. Combine like terms.

half ofthe x Add Take this number toequation create a square. To. Use keep balanced, subtract 1 completing the coefficient and square it. a total of 0 has been perfectassquare trinomial. well. This way, added to the right side of the equation. Factor the perfect square trinomial. Combine like terms. Factor out the GCF of the terms with variables. keep theof equation add 8 as To. Take half the x balanced, Add this number to create a Useway, completing square. well. This a total it. ofthe 0 has been added coefficient and square perfect square trinomial. to the right side of the equation. Factor the perfect square trinomial and combine like terms.

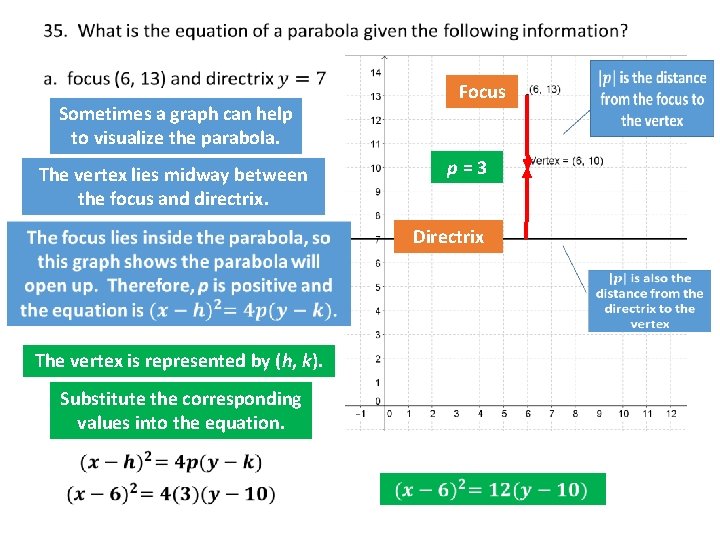
Focus Sometimes a graph can help to visualize the parabola. p=3 The vertex lies midway between the focus and directrix. Directrix The vertex is represented by (h, k). Substitute the corresponding values into the equation.

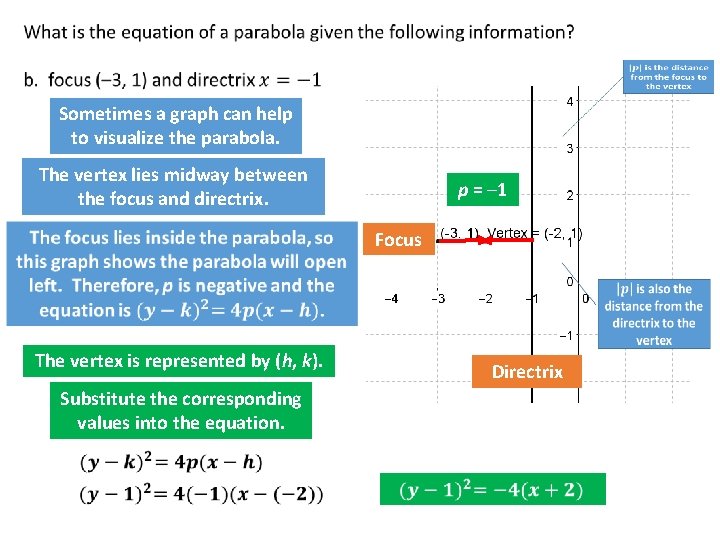
Sometimes a graph can help to visualize the parabola. The vertex lies midway between the focus and directrix. p = – 1 Focus The vertex is represented by (h, k). Directrix Substitute the corresponding values into the equation.

Set the equation equal to 0. Divide both sides of the equation by – 1 to create a positive leading coefficient. Substitute the x-values into one of the equations to solve for the corresponding y-values. Factor and solve. and

Collect like terms. Set the equation equal to 0. Factor and solve. and Substitute the x-values into one of the equations to solve for the corresponding y-values.

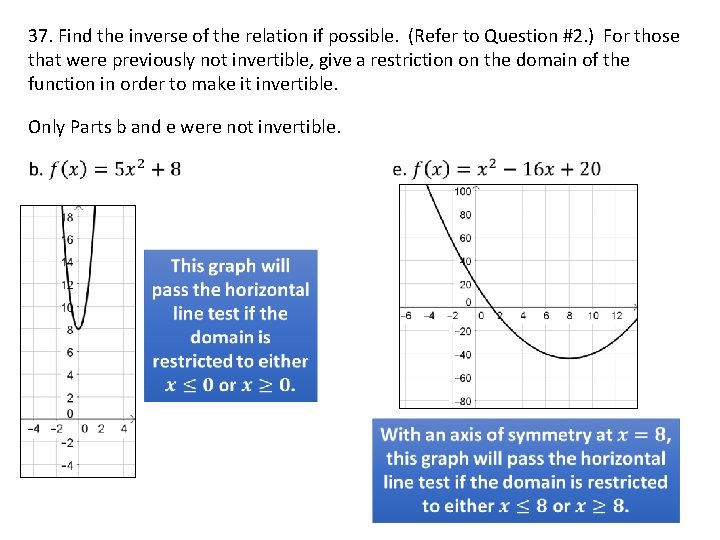
37. Find the inverse of the relation if possible. (Refer to Question #2. ) For those that were previously not invertible, give a restriction on the domain of the function in order to make it invertible. Only Parts b and e were not invertible.

38. Name all of the operations under which polynomials are closed. Addition, Subtraction and Multiplication 39. Is the set of whole numbers closed under a. Addition? Remember whole numbers are 0, 1, 2, 3, …. Adding whole numbers will result in equivalent or larger whole numbers, so YES b. Subtraction? c. Multiplication? d. Division? Multiplying whole numbers will result in equivalent or larger whole numbers, so YES

Make sure the equation is written in standard form. Then look to the leading term to determine end behavior. The polynomial is even (degree of 4), so the end behavior will either be up on the left and right, or down on the left and right. Since the leading coefficient is positive, the end behavior goes up on the left and right. The polynomial is odd (degree of 3), so the end behavior will either be down on the right and up on the left or up on the right and down on the left. Since the leading coefficient is positive, the end behavior goes down on the left and up on the right.

Identify the zeros of the polynomial. Factor out the GCF of 2. Use the Rational Root Theorem or other tools to test possible zeros. Let’s test +2 using synthetic division. 2 is a zero! Let’s test +2 again using synthetic division to see if it is a double root. Factor. Zeros = – 1 and 2, each with a multiplicity of 2.

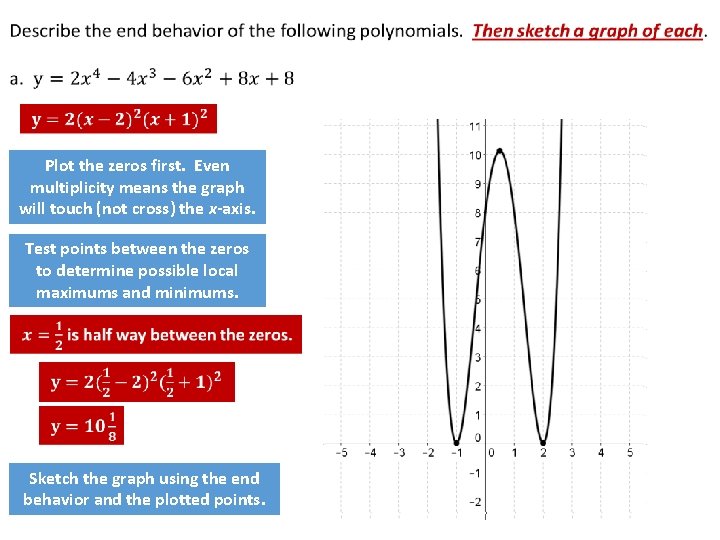
Plot the zeros first. Even multiplicity means the graph will touch (not cross) the x-axis. Test points between the zeros to determine possible local maximums and minimums. Sketch the graph using the end behavior and the plotted points.

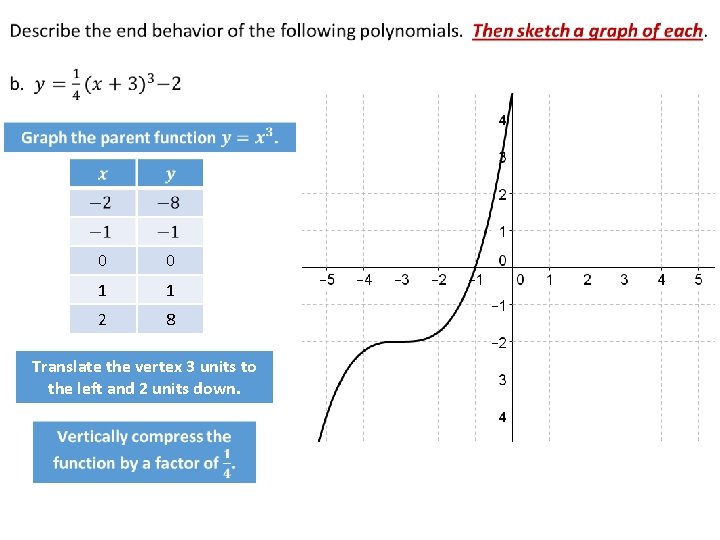
0 0 1 1 2 8 Translate the vertex 3 units to the left and 2 units down.

Set each factor equal to 0. Use the quadratic formula to solve. and a = 4 b = 2 c = 1 Substitute the values for a, b, and c into the formula. Simplify. Simplify using a factor of 2.

Set the equation equal to 0. Set each factor equal to 0. Use the quadratic formula to solve. and a = 1 b = -5 c = 25 Substitute the values for a, b, and c into the formula. Simplify.

Factor again – difference of squares. Set each factor equal to zero. Set the equation equal to zero. Factor by grouping. Factor again – difference of squares. Set each factor equal to zero.

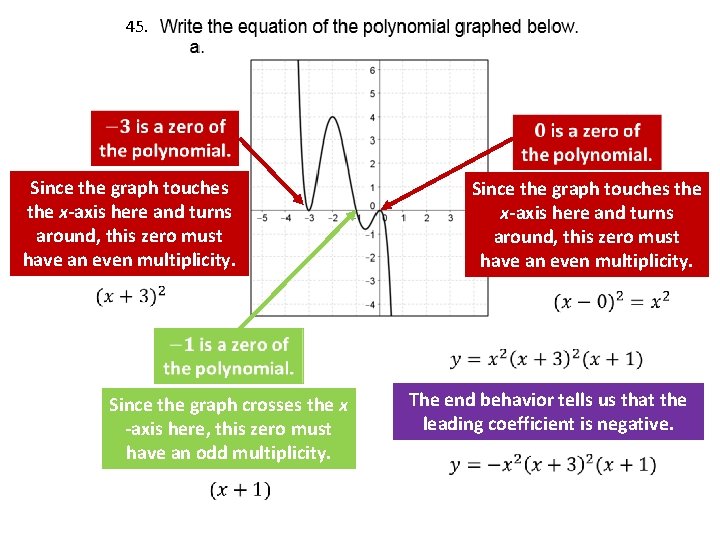
45. Since the graph touches the x-axis here and turns around, this zero must have an even multiplicity. Since the graph crosses the x -axis here, this zero must have an odd multiplicity. The end behavior tells us that the leading coefficient is negative.

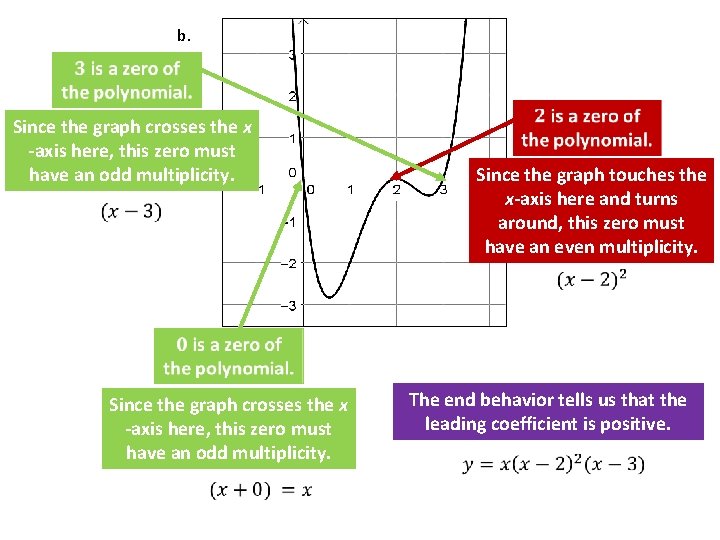
b. Since the graph crosses the x -axis here, this zero must have an odd multiplicity. Since the graph touches the x-axis here and turns around, this zero must have an even multiplicity. Since the graph crosses the x -axis here, this zero must have an odd multiplicity. The end behavior tells us that the leading coefficient is positive.

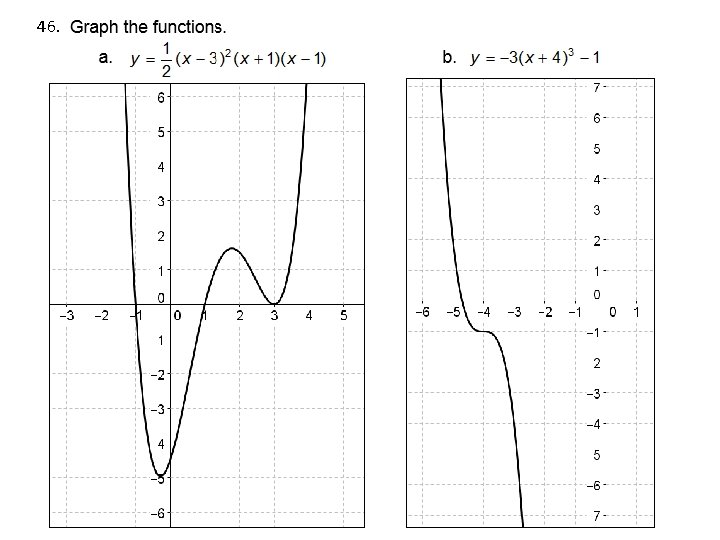
46.

Since the remainder is 0, 2 is a zero of the polynomial.

48. Find the solutions to the following equations and name any extraneous solutions that arise. Factor the denominator to a. find all of the factors needed for a common denominator. Clear the denominator. Factor and solve.

Factor the denominator to find all of the factors needed for a common denominator. b. Set the equation = 0 and combine numerators with a common denominator. Clear the denominator and simplify. Factor and solve.

49. Find the value(s) of x for which f(x) = g(x). Name any extraneous solutions that arise. a. Cross multiply b. Simplify Cross multiply Set the quadratic equal to 0 and solve.

50. Name any vertical and horizontal asymptotes of the graphs of the following equations. a. VA: Set the denominator = to 0 and solve. HA: BOB 0 BOTN EATS DC BOB 0

50. Name any vertical and horizontal asymptotes of the graphs of the following equations. b. Simplify the fraction VA: HA: EATS DC

50. Name any vertical and horizontal asymptotes of the graphs of the following equations. c. Factor to see if the fraction can be simplified. The numerator is not factorable. Look to the degree of the numerator and the degree of the denominator for the horizontal asymptote. Since the degree of the numerator = the degree of the denominator, divide the leading coefficients. Degree = 2

50. Name any vertical and horizontal asymptotes of the graphs of the Degree = 1 following equations. d. The denominator is not factorable. Degree = 2 There are no vertical asymptotes.