Matematika Sistem Informasi ALJABAR BOOLEAN Aljabar Boolean Definisi

Matematika Sistem Informasi ALJABAR BOOLEAN

Aljabar Boolean Definisi Aljabar Boolean Prinsip Dualitas Sifat-sifat Aljabar Boolean Daftar Isi Fungsi Boolean Fungsi Kompleman Bentuk Kanonik Aplikasi Aljabar Boolean
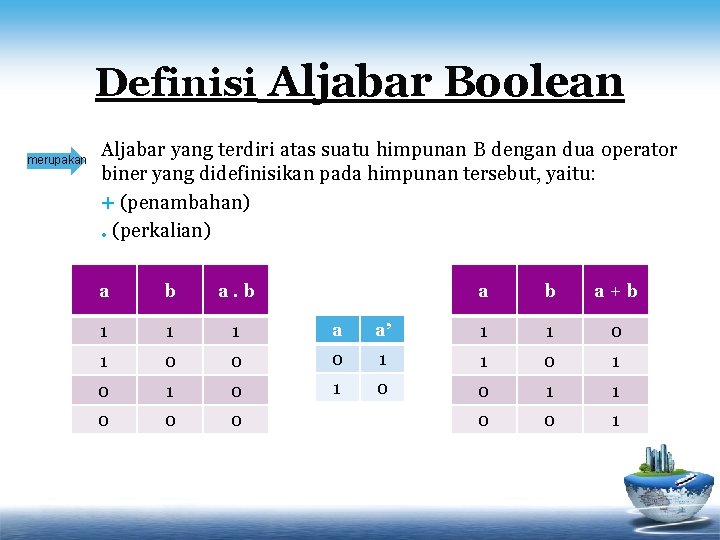
Definisi Aljabar Boolean merupakan Aljabar yang terdiri atas suatu himpunan B dengan dua operator biner yang didefinisikan pada himpunan tersebut, yaitu: + (penambahan). (perkalian) a b a+b 1 1 1 a a’ 1 1 0 0 0 1 1 0 1 0 0 1 1 0 0 0 1

Definisi Aljabar Boolean Perbedaan antara Aljabar Boolean dengan Aljabar Biasa ü Hukum distributif + dan. benar untuk aljabar boolean, tetapi tidak benar untuk aljabar biasa ü Aljabar boolean tidak memiliki operasi pembagian dan pengurangan ü Aljabar biasa memperlakukan bilangan riil dengan himpunan elemen yang tidak berhingga, sedangkan aljabar boolean memperlakukan himpunan elemen B yang sampai sekarang belum didefinisikan, tetapi pada aljabar boolean dual-nilai B didefinisikan sebagai himpunan dengan hanya dua nilai, yaitu 0 dan 1

Prinsip Dualitas Misal, S adalah kesamaan tentang aljabar Boolean, maka dual dari S atau S* diperoleh dengan cara mengganti : . dengan + 0 dengan 1 + dengan. 1 dengan 0 Tentukan dual dari: C 1. a. (b + c) = (a. b) + (a. c) O 2. a + 0 Jawab : N T 1. a + (b. c) = (a + b). (a + c) O 2. a. 0 H
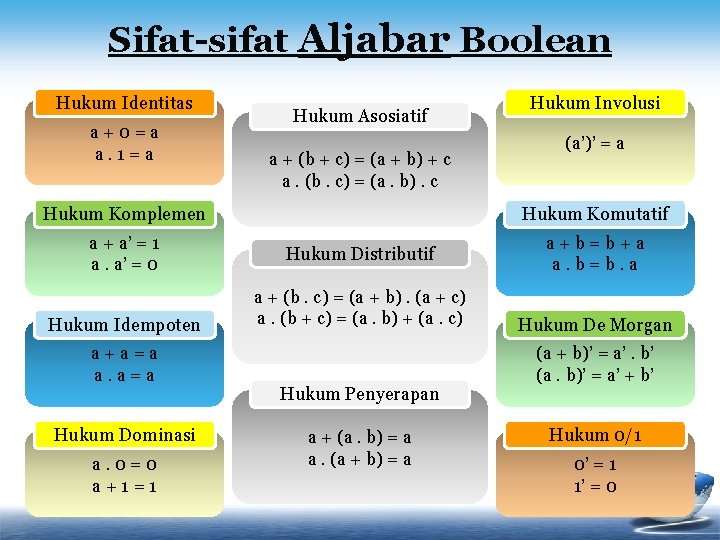
Sifat-sifat Aljabar Boolean Hukum Identitas a+0=a a. 1=a Hukum Asosiatif a + (b + c) = (a + b) + c a. (b. c) = (a. b). c Hukum Komplemen a + a’ = 1 a. a’ = 0 Hukum Idempoten a+a=a a. a=a Hukum Dominasi a. 0=0 a+1=1 Hukum Involusi (a’)’ = a Hukum Komutatif Hukum Distributif a + (b. c) = (a + b). (a + c) a. (b + c) = (a. b) + (a. c) Hukum Penyerapan a + (a. b) = a a. (a + b) = a a+b=b+a a. b=b. a Hukum De Morgan (a + b)’ = a’. b’ (a. b)’ = a’ + b’ Hukum 0/1 0’ = 1 1’ = 0

Sifat-sifat Aljabar Boolean CONTOH Buktikan bahwa untuk sembarang elemen a dan b dari aljabar Boolean : a+a. b=a Jawab: a+a. b=a. 1+a. b = a. (1 + b) =a. 1 =a (Identitas) (Distributif) (Dominasi) (Identitas) a b a+a. b 1 1 1 0 0 0

Fungsi Boolean Pada aljabar dua-nilai, B = (0, 1). Peubah (variabel) x disebut peubah boolean atau peubah biner, jika nilainya hanya dari B. Fungsi Boolean ( Fungsi Biner ) à Ekspresi yang dibentuk dari peubah biner, dua buah operator biner (+ dan. ) , operator uner komplemen ( ¯ ), tanda kurung, dan tanda sama dengan (=). Setiap peubah boolean, termasuk komplemennya, disebut literal. Contoh-contoh fungsi Boolean : 1. f(x) = x 2. f(x, y) = x’y + xy’ + y’ 3. f(x, y) = x’y’ 4. f(x, y) = (x + y)’ 5. f(x, y) = xyz’
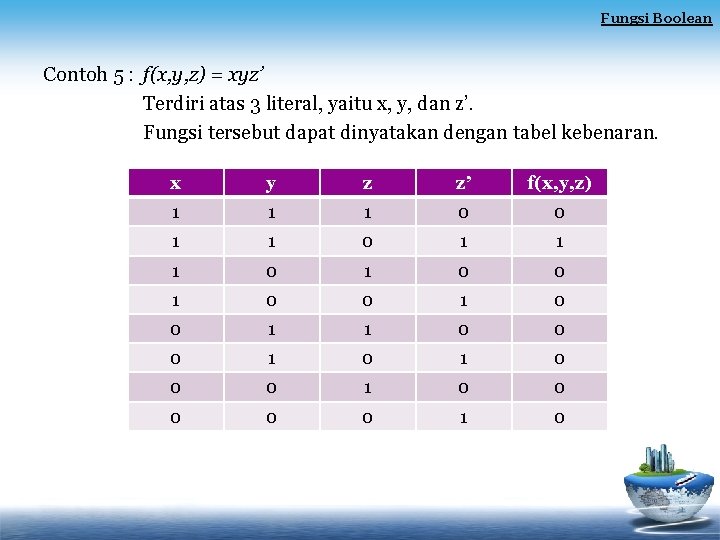
Fungsi Boolean Contoh 5 : f(x, y, z) = xyz’ Terdiri atas 3 literal, yaitu x, y, dan z’. Fungsi tersebut dapat dinyatakan dengan tabel kebenaran. x y z z’ f(x, y, z) 1 1 1 0 0 1 0 0 1 1 0 0 0 1 0

Fungsi Boolean Penyederhanaan Fungsi Boolean seringkali mengandung operasi-operasi biner yang tidak perlu, literal atau suku-suku yang berlebihan. Dari segi penerapan, fungsi Boolean yang lebih sederhana berarti rangkaian logikanya juga sederhana. Penyederhanaan fungsi Boolean disebut juga minimisasi fungsi. Penyederhanaan fungsi Boolean dapat dilakukan dengan 3 cara, yaitu: 1. Secara aljabar, menggunakan rumus-rumus/aksioma-aksioma yang berlaku pada fungsi Boolean. 2. Menggunakan Peta Karnaugh 3. Menggunakan metode Quine Mc Cluskey (metode Tabulasi).

Fungsi Komplemen Fungsi komplemen dari suatu fungsi f, yaitu f’ dapat dicari dengan menukarkan nilai 0 menjadi 1 dan 1 menjadi 0. Untuk n buah peubah, Cara 1 Hukum De Morgan x 1, x 2, . . . , xn : (x 1 + x 2 +. . . + xn)’ = x 1’x 2’. . . Xn’ dan dualnya Contoh : f (x, y, z) = x (y’z’ + yz) maka, f’ (x, y, z) = x ( y’z’ + yz) = x’ + (y’z’ + yz)’ = x’ + (y’z’)’ + (yz)’ = x’ + (y + z) (y’ + z’) (x 1. x 2. . . xn)’ = x 1’ + x 2’ +. . . + xn’ Cara 2 Prinsip Dualitas Cari dual dari f, lalu komplemenkan setiap literalnya Contoh : f (x, y, z) = x (y’z’ + yz) maka, f’ (x, y, z) = x ( y’z’ + yz) = x + (y’ + z’ ) (y + z) = x’ + (y + z) (y’ + z’)

Bentuk Kanonik Fungsi Boolean yang dinyatakan sebagai jumlah dari hasil kali, hasil kali dari jumlah, dengan setiap suku mengandung literal lengkap, disebut bentuk kanonik. Ada 2 macam bentuk kanonik, yaitu: Minterm atau Sum of Product (SOP) Untuk membentuk minterm, tinjau kombinasi peubah-peubah yang menghasilkan nilai 1. Kombinasi 001, 100, dan 111 ditulis sebagai x’y’z, xy’z’, dan xyz. Maxterm atau Product of Sum (POS) Untuk membentuk maxterm, tinjau kombinasi peubah-peubah yang menghasilkan nilai 0. Kombinasi 000, 010, 101, dan 110 ditulis sebagai x’y’z’, x’yz’, xy’z, dan xyz’.

Bentuk Kanonik Minterm dan Maxterm dari dua peubah biner x y 0 Minterm Maxterm Suku Lambang 0 x’ y’ m 0 x+y M 0 0 1 x’ y m 1 x + y’ M 1 1 0 x y’ m 2 x’ + y M 2 1 1 xy m 3 x’ + y’ M 3
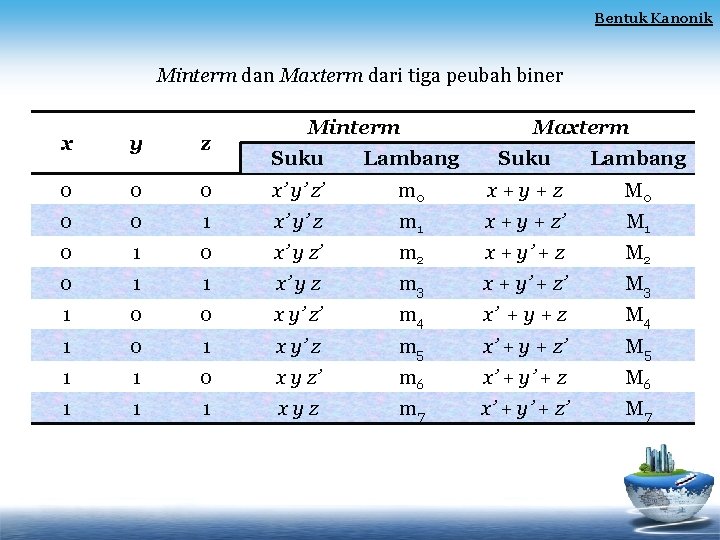
Bentuk Kanonik Minterm dan Maxterm dari tiga peubah biner x y z 0 0 0 Minterm Maxterm Suku Lambang 0 x’ y’ z’ m 0 x+y+z M 0 0 1 x’ y’ z m 1 x + y + z’ M 1 0 x’ y z’ m 2 x + y’ + z M 2 0 1 1 x’ y z m 3 x + y’ + z’ M 3 1 0 0 x y’ z’ m 4 x’ + y + z M 4 1 0 1 x y’ z m 5 x’ + y + z’ M 5 1 1 0 x y z’ m 6 x’ + y’ + z M 6 1 1 1 xyz m 7 x’ + y’ + z’ M 7

Bentuk Kanonik Contoh : Tinjau fungsi Boolean yang diekspresikan dalam bentuk tabel kebenaran di bawah ini. Nyatakan fungsi tersebut dalam bentuk kanonik SOP dan POS ! x y z f (x, y, z) 0 0 0 1 1 0 1 0 1 1 0 0 1 1 Jawab 1. SOP (tinjau kombinasi peubah yang menghasilkan nilai 1) f(x, y, z) = x’y’z + xy’z’ + x y z = m 1 + m 4 + m 7 = ( 1, 4, 7) 2. POS (tinjau kombinasi peubah yang menghasilkan nilai 0) f(x, y, z) = (x + y + z) (x + y’ + z’) (x’ + y’ + z) = M 0 M 2 M 3 M 5 M 6 = ( 0, 2, 3, 5, 6)
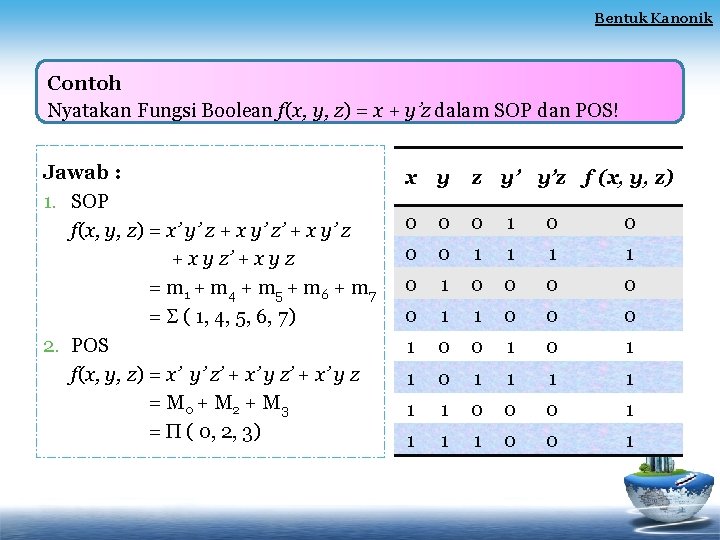
Bentuk Kanonik Contoh Nyatakan Fungsi Boolean f(x, y, z) = x + y’z dalam SOP dan POS! Jawab : 1. SOP f(x, y, z) = x’ y’ z + x y’ z’ + x y’ z + x y z’ + x y z = m 1 + m 4 + m 5 + m 6 + m 7 = ( 1, 4, 5, 6, 7) 2. POS f(x, y, z) = x’ y’ z’ + x’ y z = M 0 + M 2 + M 3 = ( 0, 2, 3) x y z y’ y’z f (x, y, z) 0 0 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 0 0 1 1 0 0 1

Aplikasi Aljabar Boolean 1. Jaringan Pensaklaran Saklar adalah obyek yang mempunyai 2 buah keadaan (buka dan tutup). Kita dapat mengasosiasikan setiap peubah dalam fungsi Boolean sebagai gerbang “gate” di dalam sebuah saluran. Secara fisik, gerbang ini dapat berupa keran di dalam pipa hidrolik, transistor, dispatcher pada alat rumah tangga, atau sembarang alat lain yang dapat melewatkan atau menghambat aliran.
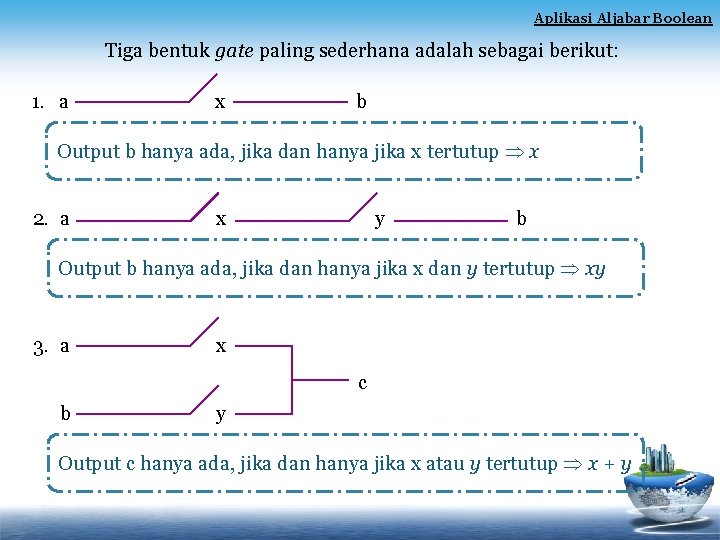
Aplikasi Aljabar Boolean Tiga bentuk gate paling sederhana adalah sebagai berikut: 1. a x b Output b hanya ada, jika dan hanya jika x tertutup x 2. a x y b Output b hanya ada, jika dan hanya jika x dan y tertutup xy 3. a x c b y Output c hanya ada, jika dan hanya jika x atau y tertutup x + y
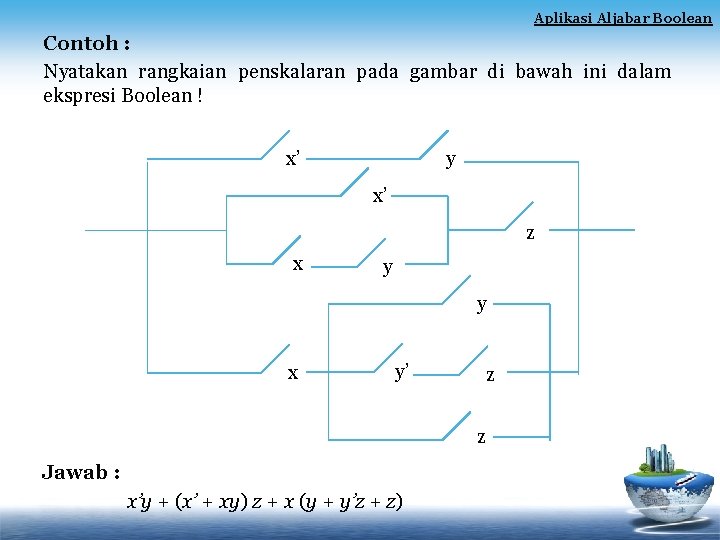
Aplikasi Aljabar Boolean Contoh : Nyatakan rangkaian penskalaran pada gambar di bawah ini dalam ekspresi Boolean ! x’ y x’ z x y y x y’ z z Jawab : x’y + (x’ + xy) z + x (y + y’z + z)

2. Rangkaian Digital Elektronik Rangkaian digital elektronikbiasanya dimodelkan dalam bentuk gerbang logika. Ada 3 macam gerbang dasar: AND, OR, dan NOT. Rangkaian yang dibentuk oleh gerbang logika disebut rangkaian logika. Secara fisik, rangkaian logika diimplementasikan dalam rangkaian listrik spesifik (di luar pembahasan bab ini). x y xy Gerbang AND dua-masukan x y x+y Gerbang OR dua-masukan x x’ Gerbang NOT

Aplikasi Aljabar Boolean Contoh : Nyatakan fungsi f(x, y, z) = xy + x’y ke dalam rangkaian logika ! Jawab : x xy y xy + x’y x y x’ x’y

TUGAS 1. Nyatakan bahwa untuk sembarang elemen a dan b dari aljabar Boolean berikut ini: a + a’b = a + b 2. Cari komplemen dari fungsi f(x, y, z) = x’ (yz’ + y’z)! 3. Nyatakan fungsi Boolean f(x, y, z) = xy + x’z dalam bentuk kanonik SOP dan POS! Tugas dikumpulkan via email ke alamat kartinihalief@staff. gunadarma. ac. id Dengan subjek : AB, (Kelas)-(Kelompok ke-. . . ) Penerimaan terakhir pukul 21. 00 WIB hari ini.
- Slides: 22