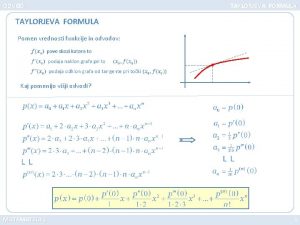
Odvod Kako merimo hitrost spreminjanja funkcije glede na

Odvod Kako merimo hitrost spreminjanja funkcije glede na spremembo argumenta? Diferenčni količnik je povprečna hitrost spreminjanja funkcije f na intervalu med x 0 in x 1. ‘Trenutna’ hitrost je

Primer: Alternativni zapis: vpeljemo novo spremenljivko h=x-x 0

F I Z I K A L N I P O M E N O D V O D A x=x(t) pot v odvisnosti od časa t povprečna hitrost v času od t 0 do t 1 trenutna hitrost v t 0 v(t) hitrost gibanja v času t Dv(t 0) pospešek W(t) toplotna energija telesa v času t DW(t 0) toplotni tok Q(t) električni naboj na prevodniku v času t DQ(t 0) električni tok

G E O M E T RI J S KI P O M E N O D V O D A smerni koeficient premice, ki seka graf funkcije f v točkah T 0(x 0, f(x 0)) in T 1(x 1, f(x 1)). Df(x 0) je smerni koeficient tangente na graf funkcije f v točki T 0. T 1 T 0 x 0 Enačba tangente: x 1

A N A L I T I Č N I P O M E N O D V O D A f naraščajoča na intervalu I okoli točke x 0 Opozorilo: obratno ni res! f lokalno naraščajoča pri x 0

Računanje odvodov I. korak: funkcija odvod Predpis x ↦ Df(x) določa funkcijo f ’: A → ℝ točke, kjer je f odvedljiva odvod funkcije f

II. korak: računske operacije in sestavljanje

III. korak: odvodi osnovnih funkcij In še. . .

Višji odvodi Primeri Vrednosti višjih odvodov v neki točki f(x 0), f ''(x 0), f '''(x 0), . . . določajo celotno funkcijo

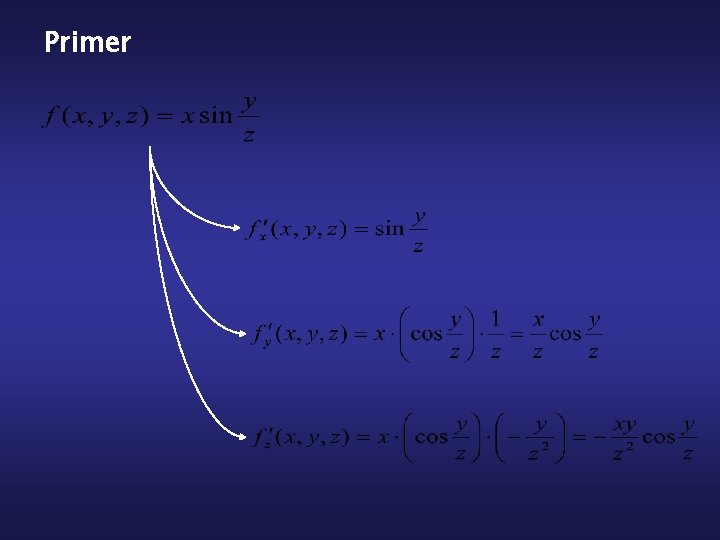
Parcialni odvod po spremenljivki T odvod po spremenljivki V funkcija n spremenljivk i -ti parcialni odvod

Primer

Zveznost in odvedljivost Kjer je f odvedljiva je tudi zvezna.

Odvedljivost in lokalni ekstremi f ima lokalni maksimum pri x 0 (tj. f(x 0) je maksimum f na intervalu I okoli x 0) in Če je f odvedljiva pri x 0 Df(x 0) =0 (stacionarna točka) Če je funkcija v lokalnem ekstremu odvedljiva, je tam njen odvod enak 0. Lokalni ekstremi odvedljive funkcije so v stacionarnih točkah.

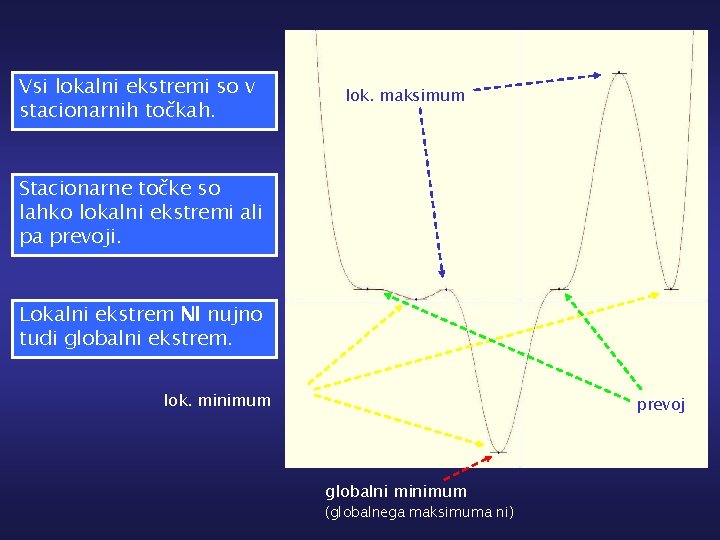
Vsi lokalni ekstremi so v stacionarnih točkah. lok. maksimum Stacionarne točke so lahko lokalni ekstremi ali pa prevoji. Lokalni ekstrem NI nujno tudi globalni ekstrem. lok. minimum prevoj globalni minimum (globalnega maksimuma ni)

Lokalni ekstremi funkcij več spremenljivk f ima lokalni maksimum pri (x 1, . . . , xn) za vsako spremenljivko posebej vsi parcialni odvodi so enaki 0 kandidati za lokalne ekstreme so rešitve sistema enačb

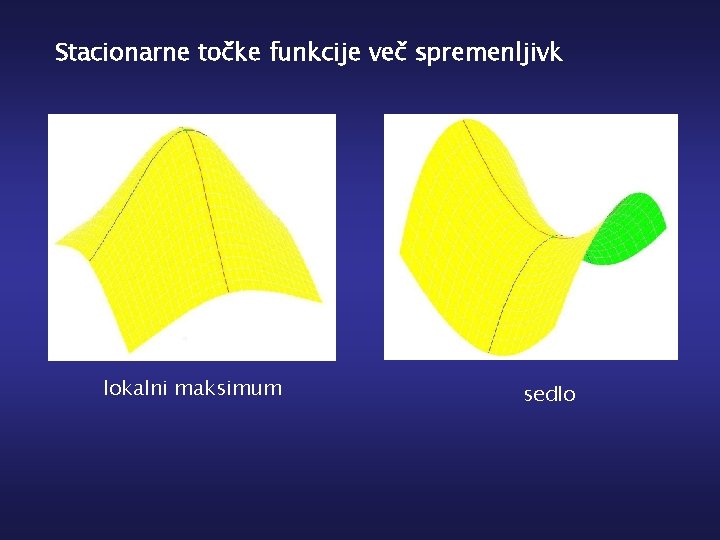
Stacionarne točke funkcije več spremenljivk lokalni maksimum sedlo

lastnosti funkcije vrednosti odvoda (naraščanje, padanje, lokalni ekstremi) . . . (predznak, ničle) ? . . . Ali lahko s pomočjo odvoda izrazimo točno vrednost diferenčnega količnika?

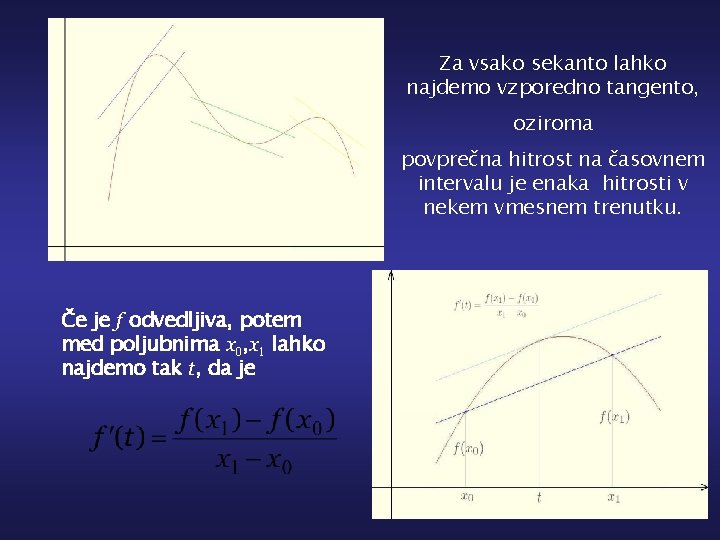
Za vsako sekanto lahko najdemo vzporedno tangento, oziroma povprečna hitrost na časovnem intervalu je enaka hitrosti v nekem vmesnem trenutku. Če je f odvedljiva, potem med poljubnima x 0, x 1 lahko najdemo tak t, da je

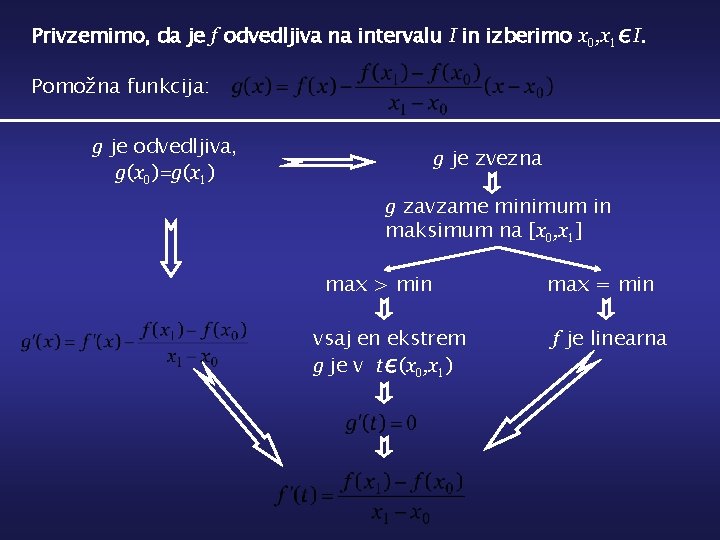
Privzemimo, da je f odvedljiva na intervalu I in izberimo x 0, x 1∊I. Pomožna funkcija: g je odvedljiva, g(x 0)=g(x 1) g je zvezna g zavzame minimum in maksimum na [x 0, x 1] max > min vsaj en ekstrem g je v t∊(x 0, x 1) max = min f je linearna

Lagrangev izrek: f odvedljiva na intervalu I za poljubni točki x 0, x 1∊I obstaja tak t med x 0 in x 1 , da je alternativni opisi:

Posledice: Primer

f narašča na [a, b] f je naraščajoča na I f je padajoča na I

f strogo narašča na [a, b] Podobno: f ’<0 na [a, b] ⇒ f strogo pada na [a, b] Obratno ne velja: f(x)=x 3 strogo narašča okoli 0, vendar je f ’(0)=0

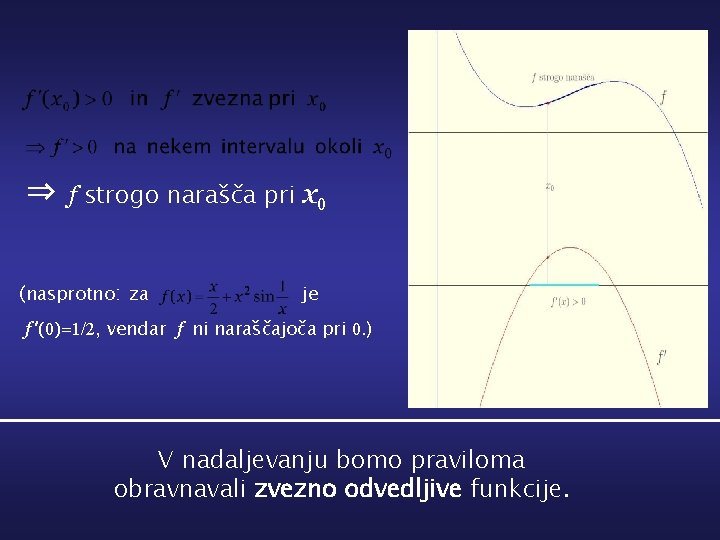
⇒ f strogo narašča pri x 0 (nasprotno: za je f ’(0)=1/2, vendar f ni naraščajoča pri 0. ) V nadaljevanju bomo praviloma obravnavali zvezno odvedljive funkcije.

Posredno odvajanje funkcij več spremenljivk f=f(u, v) + u=u(x) v=v(x) Kako bi odvajali f(u(x), v(x))? Če je funkcija f=f(u 1, . . . , un) zvezno odvedljiva in če so vsi ui odvedljive funkcije spremenljivke x, potem velja

Primer: posredni odvod

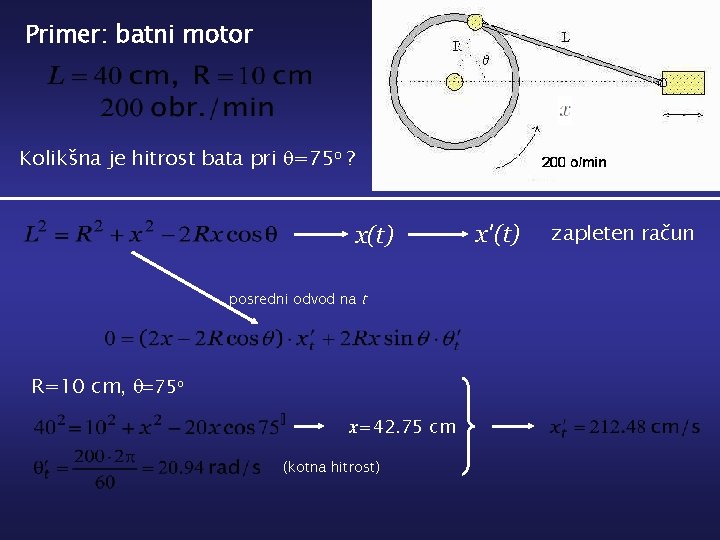
Primer: batni motor Kolikšna je hitrost bata pri q=75 o ? x(t) posredni odvod na t R=10 cm, q=75 o x=42. 75 cm (kotna hitrost) x ’(t) zapleten račun

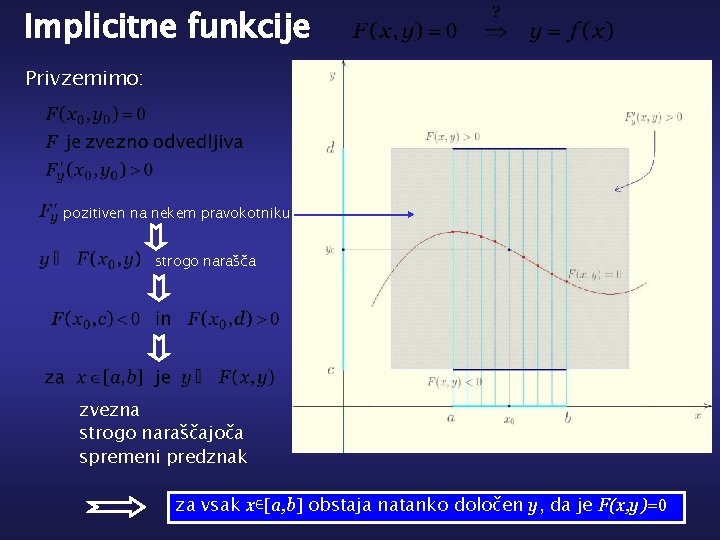
Implicitne funkcije Privzemimo: pozitiven na nekem pravokotniku strogo narašča zvezna strogo naraščajoča spremeni predznak za vsak x∊[a, b] obstaja natanko določen y, da je F(x, y)=0

Iz enačbe F(x, y)=0 lahko izrazimo y kot funkcijo x, če so v neki točki (x 0, y 0) izpolnjeni naslednji pogoji: • F(x 0, y 0)=0 • F je zvezno odvedljiva okoli (x 0, y 0) in F ’y(x 0, y 0) ≠ 0 S temi podatki je na nekem intervalu okoli x 0 natanko določena funkcija f, za katero je f(x 0)=y 0 in F(x, f(x))=0. Primer (0, 1) Rešitev okoli T(0, 1) lahko podaljšamo do točk v kateri je tangenta navpična. Dobimo jih iz pogoja F ’y=0

Odvod: povzetek Odvod je limita diferenčnega količnika. Odvod meri spreminjanje funkcije, hitrost, smerni koeficient. . . Funkcijo odvod računamo z uporabo računskih pravil (odvodi osnovnih funkcij, odvajanje računskih operacij, posredno odvajanje). Odvedljivost ima za posledico zveznost. Lokalni ekstremi so v stacionarnih točkah. Lagrangev izrek. Če je odvod funkcije na intervalu negativen/nič/pozitiven, potem je funkcija padajoča/konstantna/naraščajoča. Posredno odvajanje funkcij več spremenljivk. Implicitno podane funkcije.

Uporaba odvoda: Računanje limit Natančno risanje grafov Ekstremi funkcij ene in več spremenljivk Vezani ekstremi Izravnananje numeričnih podatkov Newtonova metoda za reševanje enačb Numerično odvajanje

Računanje limit Računamo pri pogoju (Nedoločena oblika Velja: L’Hospitalovo pravilo )

Primeri: L’Hospitalovo pravilo uporabimo tudi za in ko je

Risanje grafov (Območje definicije, obnašanje na robu, ničle, območja naraščanja in padanja, stacionarne točke, ukrivljenost, prevoji, simetrije. ) 1. Definicijsko območje: določimo na podlagi lastnosti osnovnih funkcij. 2. Rob definicijskega območja: obnašanje funkcije (pole, asimptote) izrazimo s pomočjo limit; pri računanju si pomagamo z L’Hospitalovim pravilom. 3. Ničle: določimo s pomočjo raznih, tudi približnih, metod za reševanje enačb.

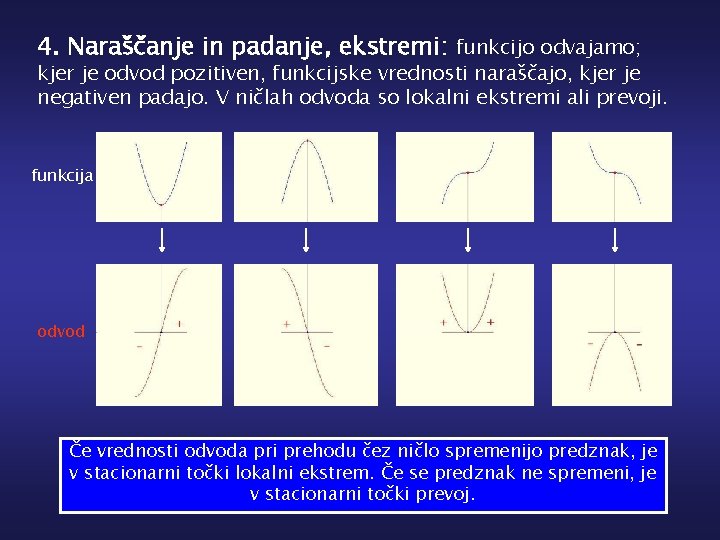
4. Naraščanje in padanje, ekstremi: funkcijo odvajamo; kjer je odvod pozitiven, funkcijske vrednosti naraščajo, kjer je negativen padajo. V ničlah odvoda so lokalni ekstremi ali prevoji. funkcija odvod Če vrednosti odvoda pri prehodu čez ničlo spremenijo predznak, je v stacionarni točki lokalni ekstrem. Če se predznak ne spremeni, je v stacionarni točki prevoj.

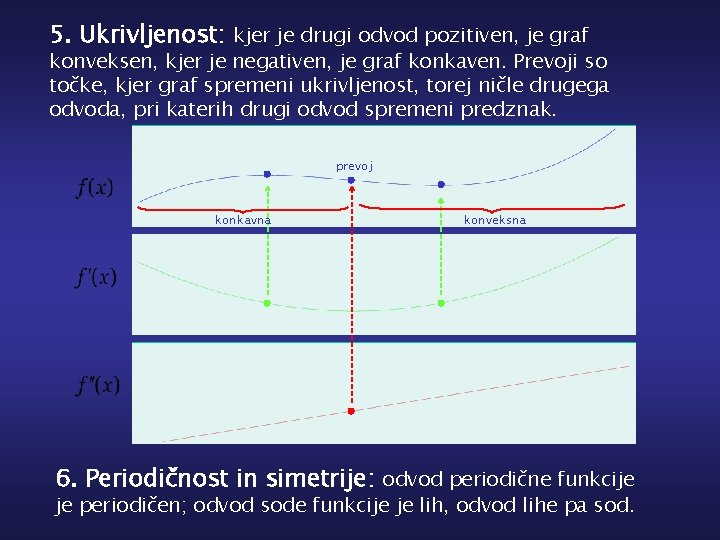
5. Ukrivljenost: kjer je drugi odvod pozitiven, je graf konveksen, kjer je negativen, je graf konkaven. Prevoji so točke, kjer graf spremeni ukrivljenost, torej ničle drugega odvoda, pri katerih drugi odvod spremeni predznak. prevoj konkavna konveksna 6. Periodičnost in simetrije: odvod periodične funkcije je periodičen; odvod sode funkcije je lih, odvod lihe pa sod.

Nariši graf Definicijsko območje: navpična asimptota (pol) x=0 vodoravna asimptota y=0 Ničle funkcije, 1. in 2. odvoda:

Globalni ekstremi Globalni ekstrem v notranjosti območja (če je funkcija odvedljiva) v stacionarni točki na robu območja (rob tvorijo točke/krivulje/ploskve/. . . ) funkcija odvisna od manj spremenljivk Vedno premislimo, ali funkcija sploh zavzame ekstrem.

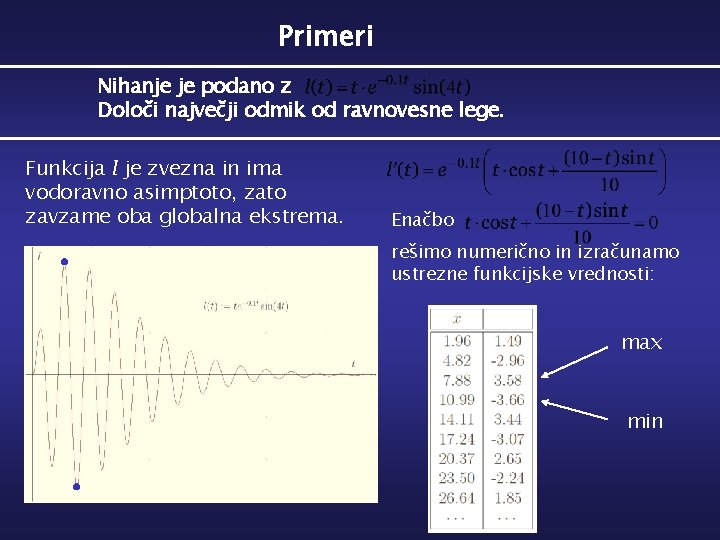
Primeri Nihanje je podano z Določi največji odmik od ravnovesne lege. Funkcija l je zvezna in ima vodoravno asimptoto, zato zavzame oba globalna ekstrema. Enačbo rešimo numerično in izračunamo ustrezne funkcijske vrednosti: l(x) max min

Poišči ekstreme funkcije f(x, y)=2 x 2+xy-y 2 -2 x+4 y na trikotniku z oglišči A(0, 1), B(3, 4), C(-1, 4). stacionarna točka T 1(0, 2); f(0, 2)=4. max C min B A

Vezani ekstremi Iščemo ekstreme funkcije f(x, y) med vsemi (x, y), ki zadoščajo pogoju G(x, y)=0. Primer Poišči točko na elipsi, določeni z enačbo (x-2)2+2(y-3)2=1, ki je najbolj oddaljena od izhodišča. Drugače povedano: poišči maksimum funkcije f(x, y) =x 2+y 2 pri pogoju G(x, y)=(x-2)2+2(y-3)2 -1=0

Običajni postopek: iz enačbe G(x, y)=0 izrazimo y in ga vstavimo v funkcijo f(x, y), ki jo potem odvajamo na x. brezupno!

Drugačen pristop: Vzdolž G(x, y)=0 je y=y(x); f(x, y(x)) odvajamo na x: odvod je izračunamo s posrednim odvajanjem G(x, y)=0; V stacionarni točki (x 0, y 0) velja (=-t)

Vpeljemo novo funkcijo Lagrangeva funkcija Pogoj za lokalni ekstrem f(x, y), vzdolž G(x, y)=0: tj. , kandidati za lokalne ekstreme f(x, y), vzdolž G(x, y)=0 so stacionarne točke Lagrangeve funkcije F=f+t. G

Primer V stacionarni točki je Enačba je 4. stopnje, rešujemo jo numerično:

Geometrični premislek: v ekstremih se krivulja G(x, y)=0 dotika nivojnic funkcije f(x, y). V teh točkah je normala vzporedna z normalo na krivuljo G(x, y)=0 na nivojnico f(x, y)=konst.

Splošno pravilo: Če iščemo ekstreme funkcije f(x 1, . . . , xn) pri pogojih Gi(x 1, . . . , xn) =0 za i=1, . . . , m vpeljemo Lagrangevo funkcijo Vezani ekstremi f so v stacionarnih točkah Lagrangeve funkcije F.

Izravnavanje numeričnih podatkov Naloga: iz tabele numeričnih podatkov (xi, yi) določi funkcijsko zvezo y=f(x), ki se s temi podatki najbolje ujema. Primer: v tabeli so podane vrednosti količine y v odvisnosti od x. Določi ustrezno funkcijsko zvezo y=f(x). Oceni vrednost y pri x =1. 5 (interpolacija) in pri x=2 (ekstrapolacija).

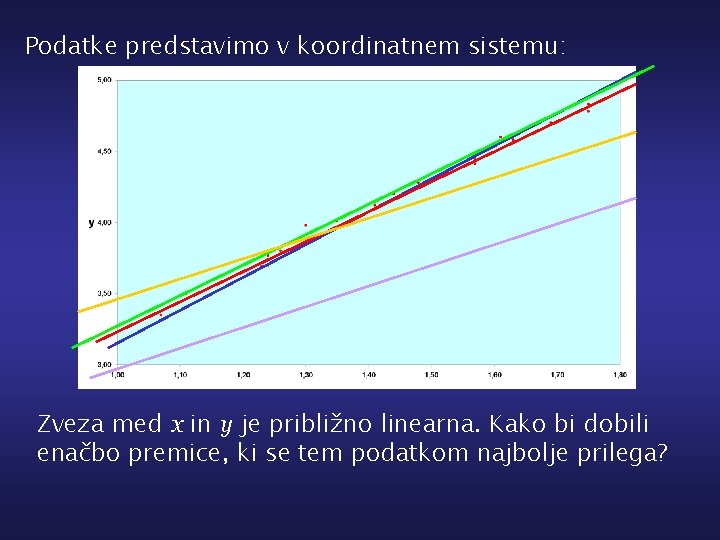
Podatke predstavimo v koordinatnem sistemu: Zveza med x in y je približno linearna. Kako bi dobili enačbo premice, ki se tem podatkom najbolje prilega?

Enačba premice y=A+Bx je odvisna od parametrov A in B. Ustreznost parametrov preskusimo na množici podatkov (xi, yi), i=1, 2, . . . , n, s pomočjo testne funkcije Če ležijo vsi podatki na premici y=A+Bx je F(A, B)=0, kar je najboljši možni rezultat. V splošnem primeru iščemo vrednosti A in B, pri katerih testna funkcija zavzame minimum. Lastnosti funkcije F: F je zvezna in odvedljiva za vse (A, B)∊ℝ 2 Ko gre A, B → ∞ narašča F čez vsako mejo, zato F zavzame minimum na ℝ 2 Ker ℝ 2 nima robnih točk, je minimum F v stacionarni točki.

Testna funkcija po kriteriju najmanjših kvadratov Sistem dveh linearnih enačb in dveh neznank: ima natanko eno rešitev, ki ustreza globalnemu minimumu testne funkcije.

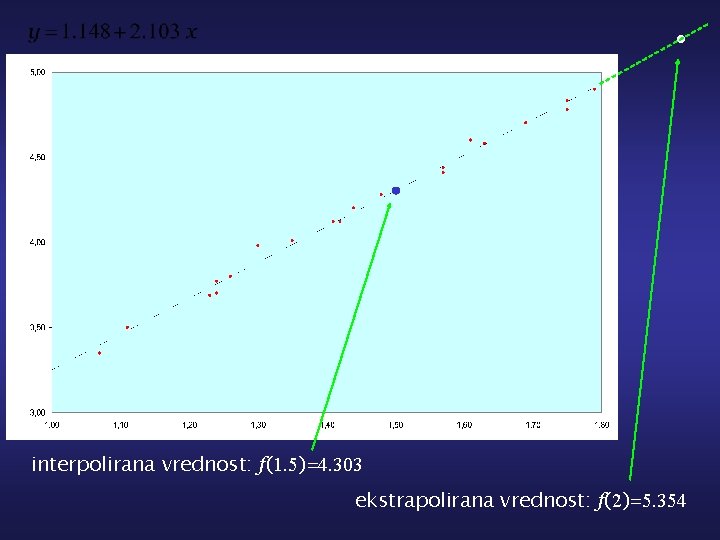
interpolirana vrednost: f(1. 5)=4. 303 ekstrapolirana vrednost: f(2)=5. 354

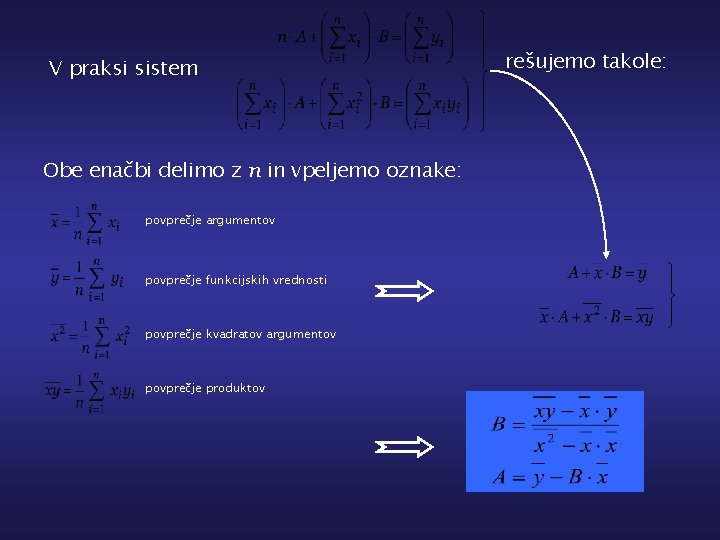
V praksi sistem Obe enačbi delimo z n in vpeljemo oznake: povprečje argumentov povprečje funkcijskih vrednosti povprečje kvadratov argumentov povprečje produktov rešujemo takole:

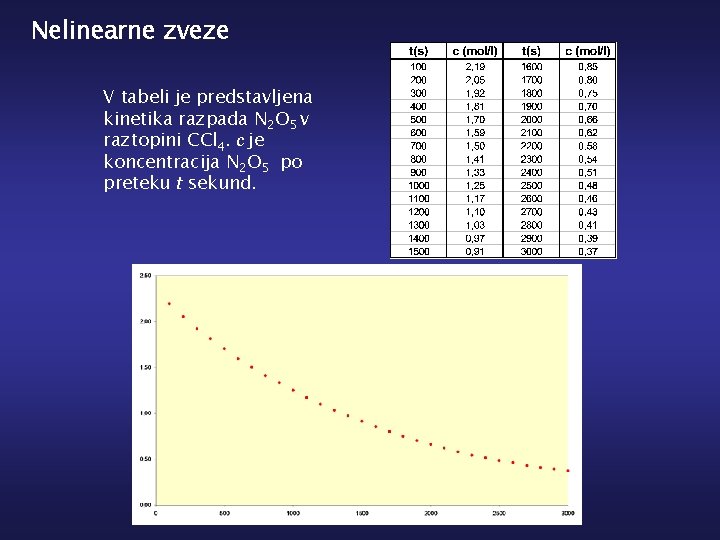
Nelinearne zveze V tabeli je predstavljena kinetika razpada N 2 O 5 v raztopini CCl 4. c je koncentracija N 2 O 5 po preteku t sekund.

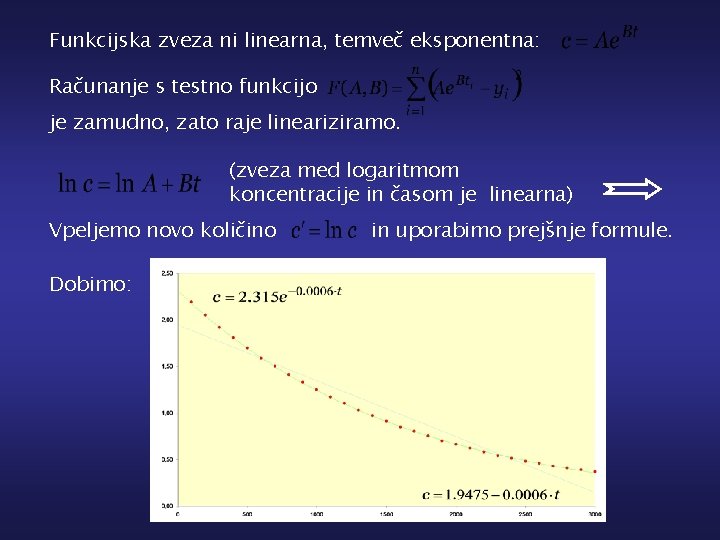
Funkcijska zveza ni linearna, temveč eksponentna: Računanje s testno funkcijo je zamudno, zato raje lineariziramo. (zveza med logaritmom koncentracije in časom je linearna) Vpeljemo novo količino Dobimo: in uporabimo prejšnje formule.

Numerično reševanje enačb Spomnimo se: x je negibna točka funkcije f, če velja f(x)=x. Če je f zvezno odvedljiva in če za negibno točko velja f ’(x)<1, potem je x privlačna negibna točka. Če začetni člen izberemo blizu privlačne negibne točke x, potem rekurzivno zaporedje xn=f(xn-1) konvergira proti x. Hitrost konvergence je večja, če je f ’(x) blizu 0.

Ideja: Enačbo g(x)=0 rešimo tako, da jo preoblikujemo v ekvivalentno enačbo oblike f(x)=x, kjer ima f čim bolj privlačne negibne točke. Newtonova iteracijska metoda

Primeri: Računanje korenov: je rešitev enačbe x 2=a Npr. a=10. Iteracijo začnemo z x 0=1: 1, 5. 5, 3. 659090, 3. 196005, 3. 162455, 3. 162277 (3. 162277 2=9. 99999582) je rešitev enačbe xn=a 1, 5, 3. 784, 2. 916439, 2. 358658, 2. 092880, 2. 033273, 2. 030548, 2. 030543 (2. 030543 2=16. 99999380) 2, 2. 03125, 2. 030543 Dober začetek je zlata vreden!

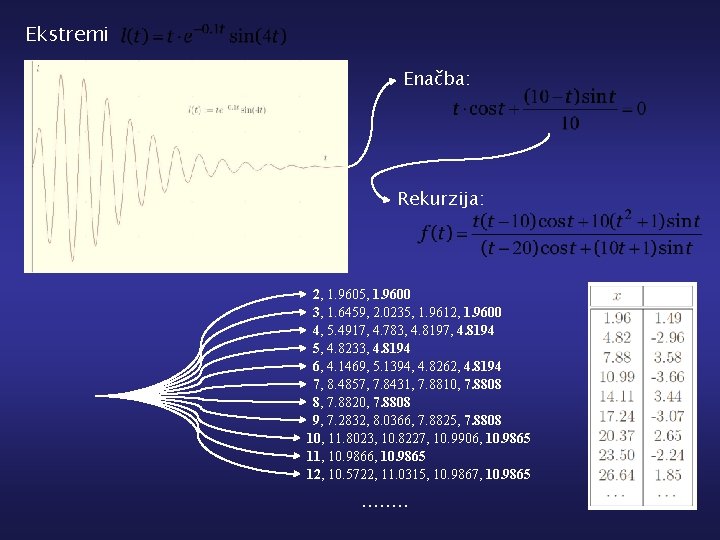
Ekstremi Enačba: Rekurzija: 2, 1. 9605, 1. 9600 3, 1. 6459, 2. 0235, 1. 9612, 1. 9600 4, 5. 4917, 4. 783, 4. 8197, 4. 8194 5, 4. 8233, 4. 8194 6, 4. 1469, 5. 1394, 4. 8262, 4. 8194 7, 8. 4857, 7. 8431, 7. 8810, 7. 8808 8, 7. 8820, 7. 8808 9, 7. 2832, 8. 0366, 7. 8825, 7. 8808 10, 11. 8023, 10. 8227, 10. 9906, 10. 9865 11, 10. 9866, 10. 9865 12, 10. 5722, 11. 0315, 10. 9867, 10. 9865 . . . . l(x)

Določi prostornino enega mola CO 2 pri temperaturi 50 o. C in pritisku 20 atmosfer. Pri teh pogojih se CO 2 ne obnaša kot idealni plin, zato uporabimo Van der Waalsovo enačbo: a ∼ interakcija med molekulami b ∼ velikost molekule Nova spremenljivka: p=20 • 1. 013 • 105 Pa = 2 026 000 Pa T=323 K a. CO 2=0. 3643 Jm 3/mol 2 b. CO 2=4. 269 • 10 -5 m 3/mol R=8. 314 J/mol K Kot začetni približek vzamemo prostornino po enačbi idealnega plina: 0. 0013254, 0. 0012274, 0. 0012266 Prostornina je 1. 23 litra.

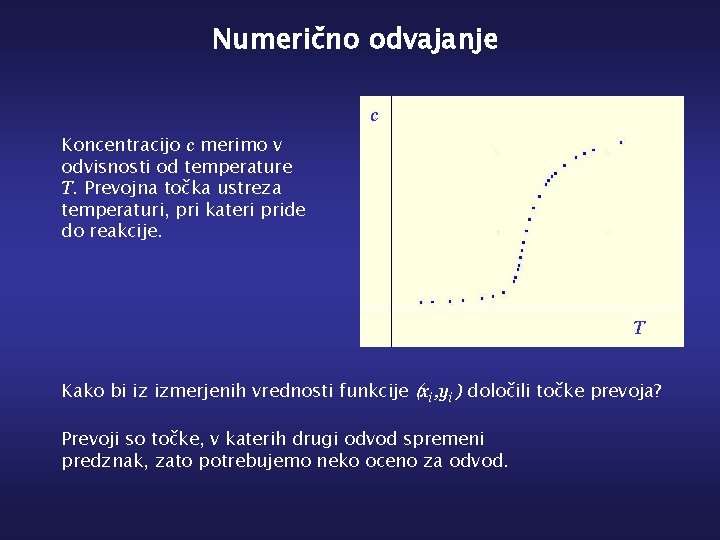
Numerično odvajanje c Koncentracijo c merimo v odvisnosti od temperature T. Prevojna točka ustreza temperaturi, pri kateri pride do reakcije. T Kako bi iz izmerjenih vrednosti funkcije (xi , yi ) določili točke prevoja? Prevoji so točke, v katerih drugi odvod spremeni predznak, zato potrebujemo neko oceno za odvod.

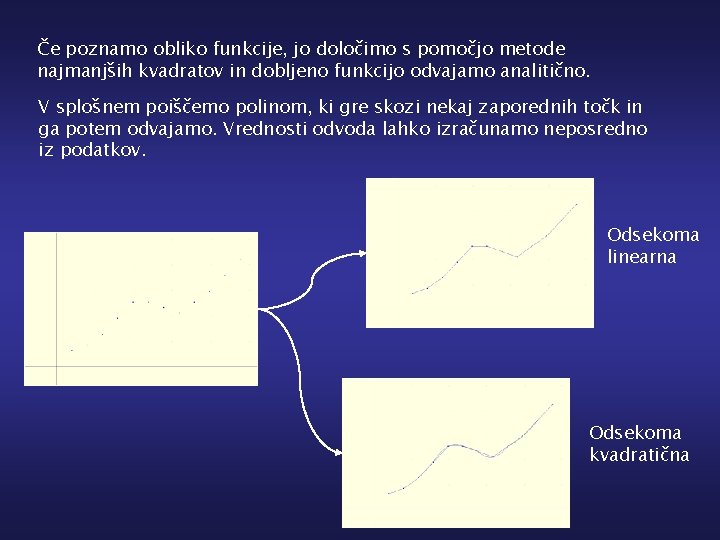
Če poznamo obliko funkcije, jo določimo s pomočjo metode najmanjših kvadratov in dobljeno funkcijo odvajamo analitično. V splošnem poiščemo polinom, ki gre skozi nekaj zaporednih točk in ga potem odvajamo. Vrednosti odvoda lahko izračunamo neposredno iz podatkov. Odsekoma linearna Odsekoma kvadratična

Formule se poenostavijo, če so točke na enakomernih razdaljah (npr. h). Za dve zaporedni točki: Za tri zaporedne točke: Za pet zaporednih točk: Numerično odvajanje je zelo občutljivo na napake v podatkih.

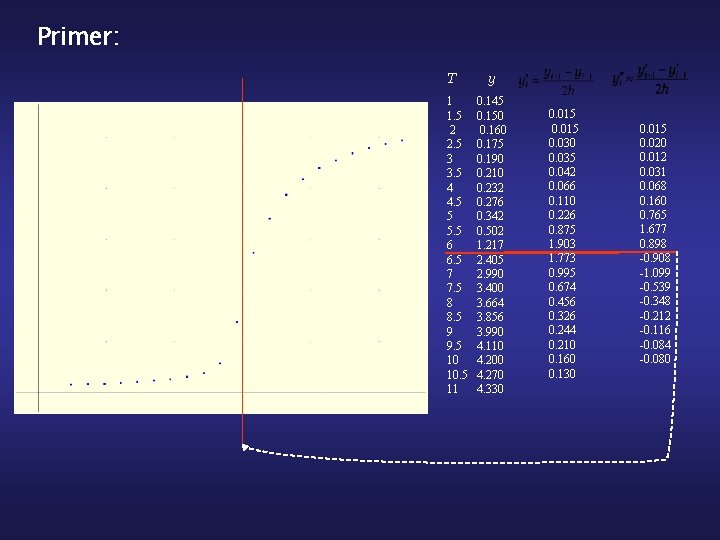
Primer: T 1 1. 5 2 2. 5 3 3. 5 4 4. 5 5 5. 5 6 6. 5 7 7. 5 8 8. 5 9 9. 5 10 10. 5 11 y 0. 145 0. 150 0. 160 0. 175 0. 190 0. 210 0. 232 0. 276 0. 342 0. 502 1. 217 2. 405 2. 990 3. 400 3. 664 3. 856 3. 990 4. 110 4. 200 4. 270 4. 330 0. 015 0. 030 0. 035 0. 042 0. 066 0. 110 0. 226 0. 875 1. 903 1. 773 0. 995 0. 674 0. 456 0. 326 0. 244 0. 210 0. 160 0. 130 0. 015 0. 020 0. 012 0. 031 0. 068 0. 160 0. 765 1. 677 0. 898 -0. 908 -1. 099 -0. 539 -0. 348 -0. 212 -0. 116 -0. 084 -0. 080