Odvod Kako opiemo hitrost spreminjanja funkcije glede na

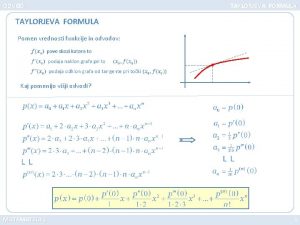
Odvod Kako opišemo hitrost spreminjanja funkcije glede na spremembo argumenta? Povprečna hitrost spremembe f v času od t 0 do t 1 : Diferenčni količnik Trenutna hitrost je

Primeri Alternativni zapis: Nova spremenljivka h=t-t 0

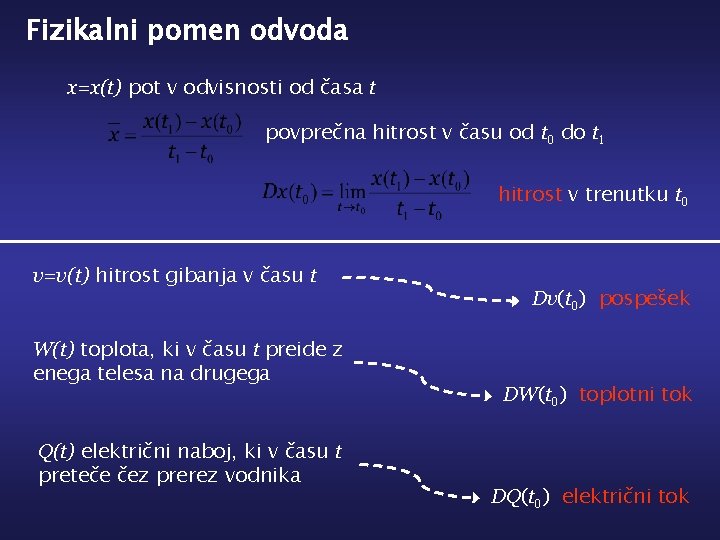
Fizikalni pomen odvoda x=x(t) pot v odvisnosti od časa t povprečna hitrost v času od t 0 do t 1 hitrost v trenutku t 0 v=v(t) hitrost gibanja v času t W(t) toplota, ki v času t preide z enega telesa na drugega Q(t) električni naboj, ki v času t preteče čez prerez vodnika Dv(t 0) pospešek DW(t 0) toplotni tok DQ(t 0) električni tok

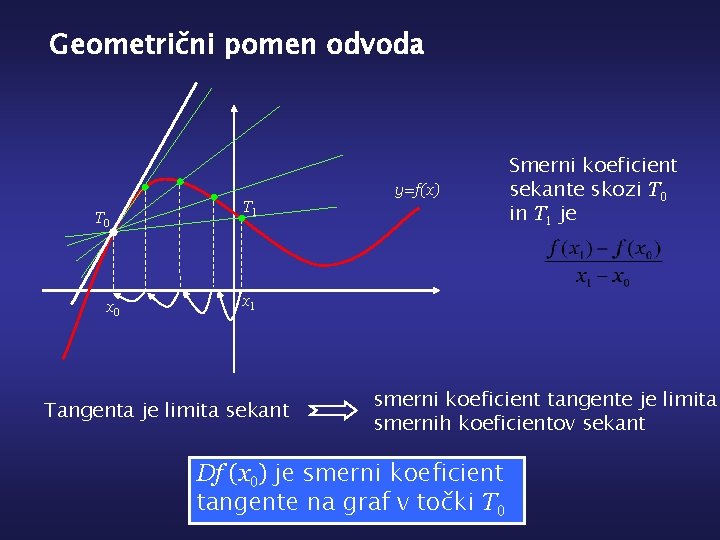
Geometrični pomen odvoda T 0 x 0 T 1 y=f(x) Smerni koeficient sekante skozi T 0 in T 1 je x 1 Tangenta je limita sekant smerni koeficient tangente je limita smernih koeficientov sekant Df (x 0) je smerni koeficient tangente na graf v točki T 0

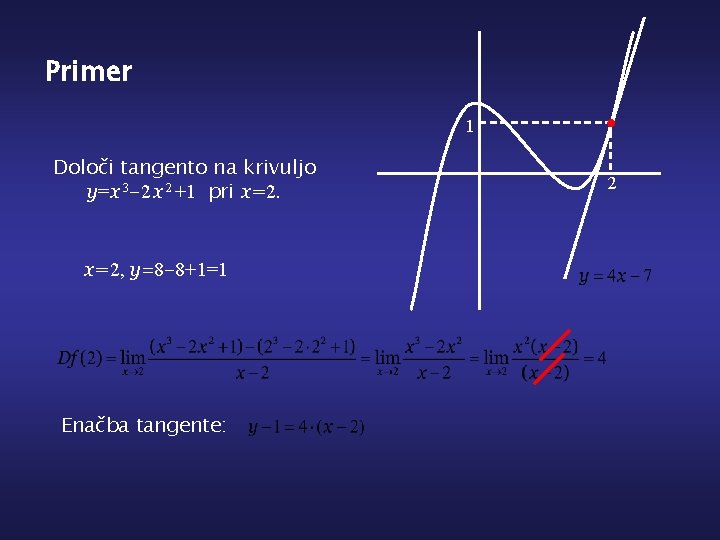
Primer 1 Določi tangento na krivuljo y=x 3 -2 x 2 +1 pri x=2, y=8 -8+1=1 Enačba tangente: 2

Odvedljivost Odvod je definiran kot limita diferenčnih količnikov, zato se lahko zgodi, da v nekaterih točkah njegova vrednost ni določena. f(x)=|x| Limita je odvisna od tega, s katere strani gre x proti 0! y=|x| Tangenta na graf je navpična!

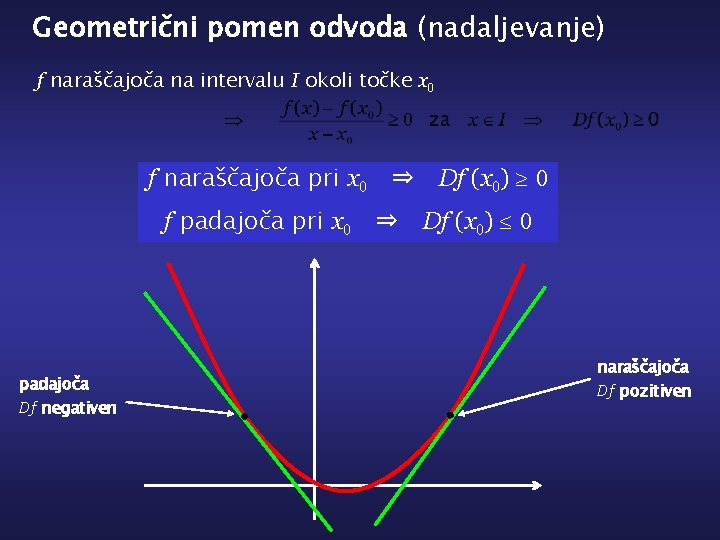
Geometrični pomen odvoda (nadaljevanje) f naraščajoča na intervalu I okoli točke x 0 f naraščajoča pri x 0 ⇒ Df (x 0) ≥ 0 f padajoča pri x 0 ⇒ Df (x 0) ≤ 0 padajoča Df negativen naraščajoča Df pozitiven

Računanje odvodov I. korak: funkcija odvod Predpis x ↦ Df(x) določa funkcijo f ' : A → ℝ. odvod funkcije f Primeri

II. korak: računske operacije in sestavljanje seštevanje (in odštevanje) množenje: deljenje: sestavljanje:

Primeri

III. korak: osnovne funkcije

Primeri

Višji odvodi Primeri Vrednosti višjih odvodov v neki točki f(x 0), f ''(x 0), f '''(x 0), . . . določajo celotno funkcijo

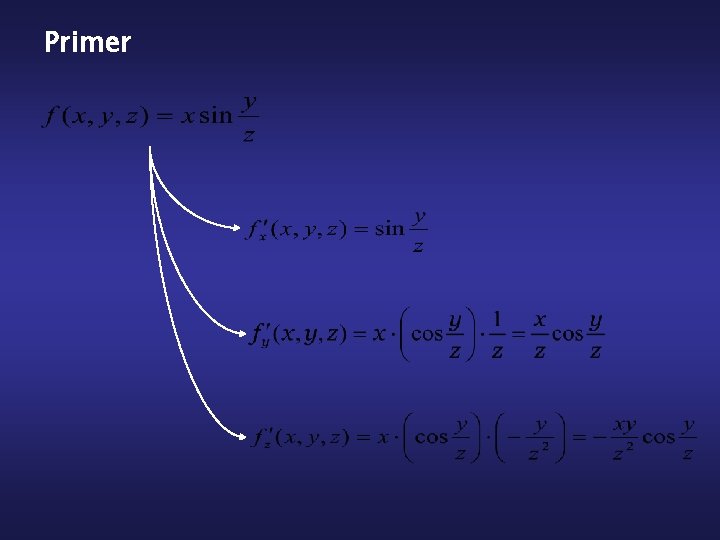
Parcialni odvod po spremenljivki T odvod po spremenljivki V funkcija n spremenljivk i -ti parcialni odvod

Primer

Lokalni ekstremi Če je f(x 0) ≥ f(x) za vse x na nekem intervalu okoli x 0 pravimo, da ima f v x 0 lokalni maksimum. Če pa je f(x 0) ≤ f(x) za vse x na nekem intervalu okoli x 0 pravimo, da ima f v x 0 lokalni minimum. Odvedljiva funkcija ima pri lokalnem ekstremu vodoravno tangento. V lokalnem ekstremu velja: f '(x 0)=0 (stacionarna točka)

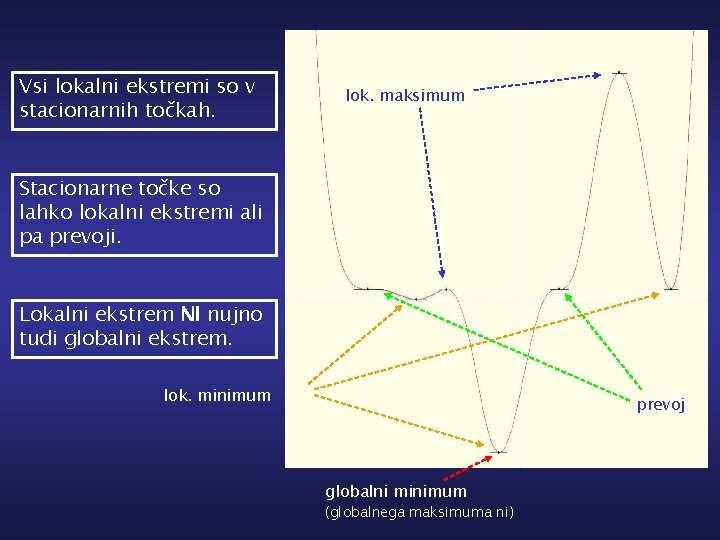
Vsi lokalni ekstremi so v stacionarnih točkah. lok. maksimum Stacionarne točke so lahko lokalni ekstremi ali pa prevoji. Lokalni ekstrem NI nujno tudi globalni ekstrem. lok. minimum prevoj globalni minimum (globalnega maksimuma ni)

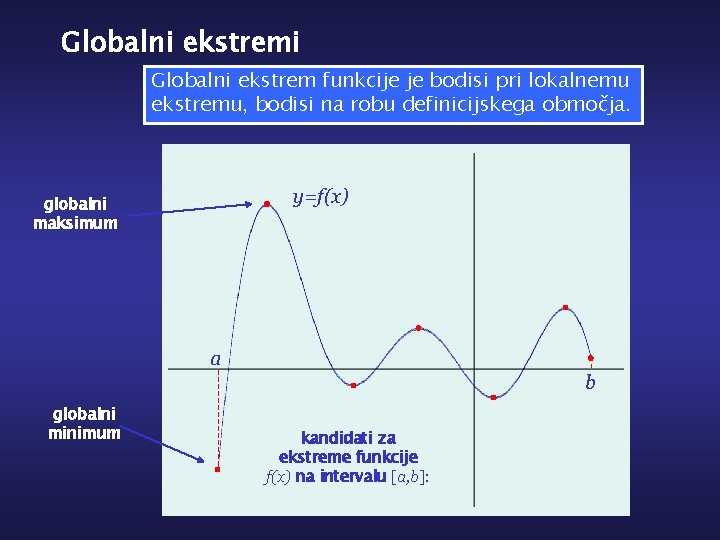
Globalni ekstremi Globalni ekstrem funkcije je bodisi pri lokalnemu ekstremu, bodisi na robu definicijskega območja. y=f(x) globalni maksimum a b globalni minimum kandidati za ekstreme funkcije f(x) na intervalu [a, b]:

Postopek za določanje globalnih ekstremov odvedljive funkcije f(x) na intervalu [a, b]: 1. Izračunamo odvod f '(x); 2. Določimo ničle odvoda, npr. x 1, x 2, . . . ; 3. Izmed vrednosti f (a), f (b), f (x 1), f (x 2), . . . določimo največjo in najmanjšo - to sta globalni maksimum in globalni minimum. Primer Določi globalne ekstreme funkcije f(x)=x 3 -4 x 2+6 na intervalu [-1, 4]. Globalni maksimum je f(0)=f(4)=6, globalni minimum je f(8/3) ≈ -3. 48

Optimizacijske naloge 1. Za katero pozitivno število je vsota števila in njegove recipročne vrednosti najmanjša? Najmanjšo vsoto dobimo pri x=1. 2. Kateri izmed pravokotnikov z obsegom 5 m ima največjo ploščino? Največjo ploščino ima kvadrat s stranico 1, 25 m.

3. Kakšne dimenzije mora imeti valjasta pločevinka s prostornino V, da bo za njeno izdelavo potrebno najmanj pločevine? r h Optimalna pločevinka ima višino enako premeru.

Lokalni ekstremi funkcij več spremenljivk f ima lokalni maksimum pri (x 1, . . . , xn) za vsako spremenljivko posebej vsi parcialni odvodi so enaki 0 kandidati za lokalne ekstreme so rešitve sistema enačb

Stacionarne točke funkcije več spremenljivk lokalni maksimum sedlo

Primeri Edina stacionarna točka je (0, 0). Stacionarni točki sta (0, 0) in .

Globalni ekstremi funkcij več spremenljivk f(x, y) je definirana na delu ravnine. Če je odvedljiva, zavzame ekstrem bodisi v stacionarni točki v notranjosti območja, ali pa na robu. Postopek za določanje globalnih ekstremov odvedljive funkcije f(x, y) na območju D ⊆ ℝ : 1. Izračunamo parcialna odvoda f x'(x, y) in f y'(x, y); 2. Določimo stacionarne točke kot rešitve enačb f x'(x, y) =0 in f y'(x, y)=0; 3. Točke na robu območja D obravnavamo kot funkcijo ene spremenljivke in poiščemo pripadajoče stacionarne točke. 4. Izmed vrednosti funkcije f v vseh stacionarnih točkah določimo največjo in najmanjšo - to sta globalni maksimum in globalni minimum.

Primer Poišči minimum in maksimum funkcije na trikotniku z oglišči A(0, 0), B(3, 0) in C(0, 3). notranjost trikotnika: C -1 daljica AB: stacionarna točka (0, 0) ni v notranjosti daljice daljica AC: A daljica BC: oglišča: minimum je f (1, 1)= -1, maksimum je f (0, 3)=12 B

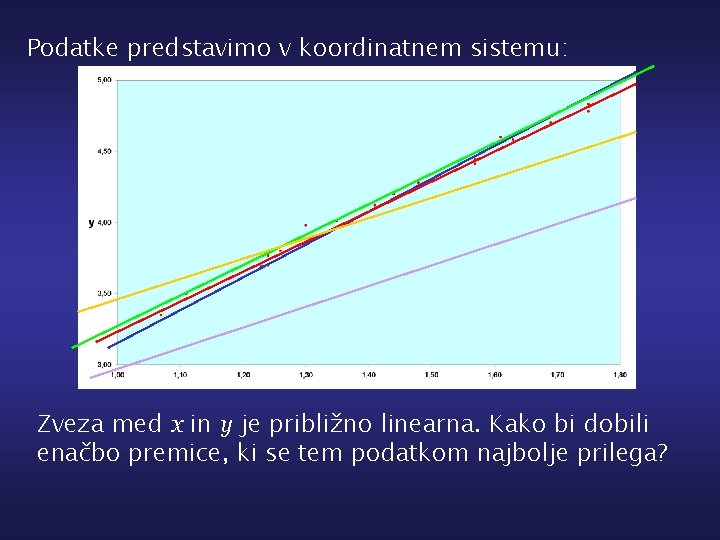
Izravnavanje numeričnih podatkov Naloga: iz tabele numeričnih podatkov (xi, yi) določi funkcijsko zvezo y=f(x), ki se s temi podatki najbolje ujema. Primer: v tabeli so podane vrednosti količine y v odvisnosti od x. Določi ustrezno funkcijsko zvezo y=f(x). Oceni vrednost y pri x =1. 5 (interpolacija) in pri x=2 (ekstrapolacija).

Podatke predstavimo v koordinatnem sistemu: Zveza med x in y je približno linearna. Kako bi dobili enačbo premice, ki se tem podatkom najbolje prilega?

Enačba premice y=A+Bx je odvisna od parametrov A in B. Ustreznost parametrov preskusimo na množici podatkov (xi, yi), i=1, 2, . . . , n, s pomočjo testne funkcije Če ležijo vsi podatki na premici y=A+Bx je F(A, B)=0, kar je najboljši možni rezultat. V splošnem primeru iščemo vrednosti A in B, pri katerih testna funkcija zavzame minimum.

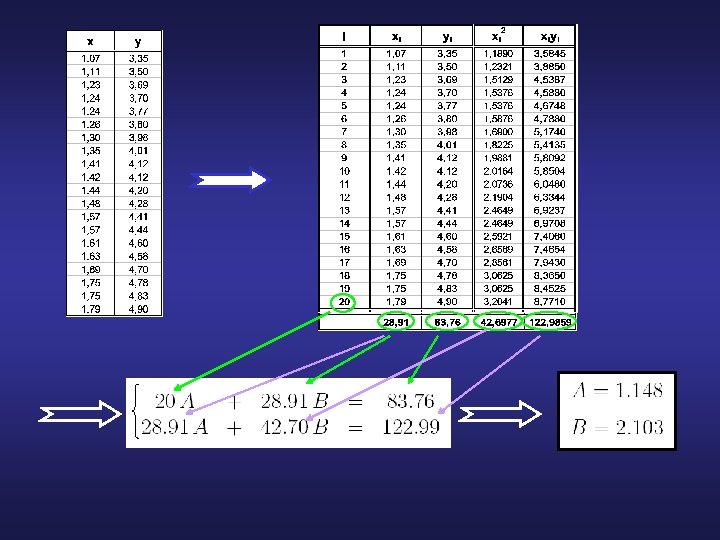
Testna funkcija po kriteriju najmanjših kvadratov Sistem dveh linearnih enačb in dveh neznank: ima natanko eno rešitev, ki ustreza globalnemu minimumu testne funkcije.

interpolirana vrednost: f(1. 5)=4. 303 ekstrapolirana vrednost: f(2)=5. 354

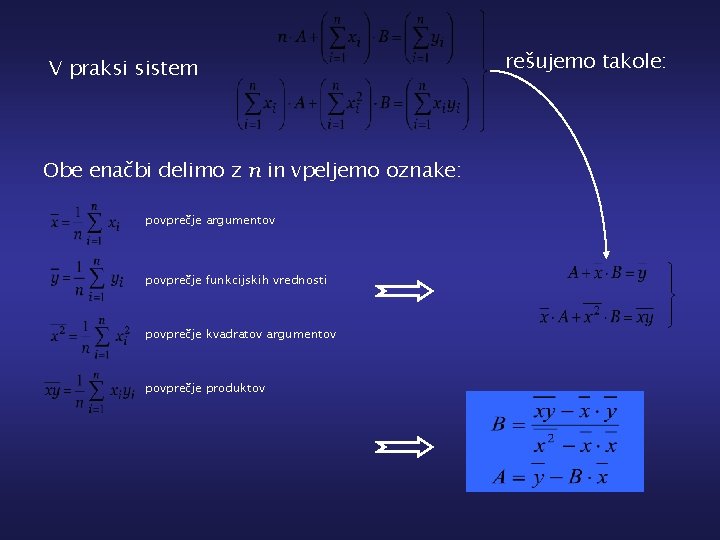
V praksi sistem Obe enačbi delimo z n in vpeljemo oznake: povprečje argumentov povprečje funkcijskih vrednosti povprečje kvadratov argumentov povprečje produktov rešujemo takole:

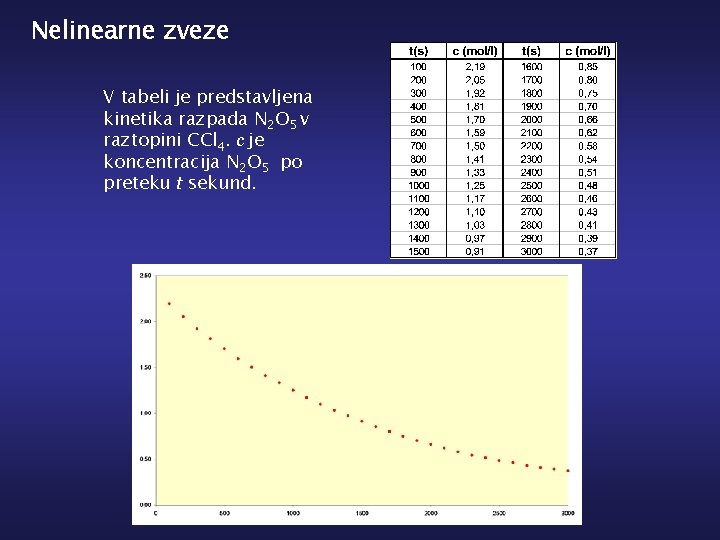
Nelinearne zveze V tabeli je predstavljena kinetika razpada N 2 O 5 v raztopini CCl 4. c je koncentracija N 2 O 5 po preteku t sekund.

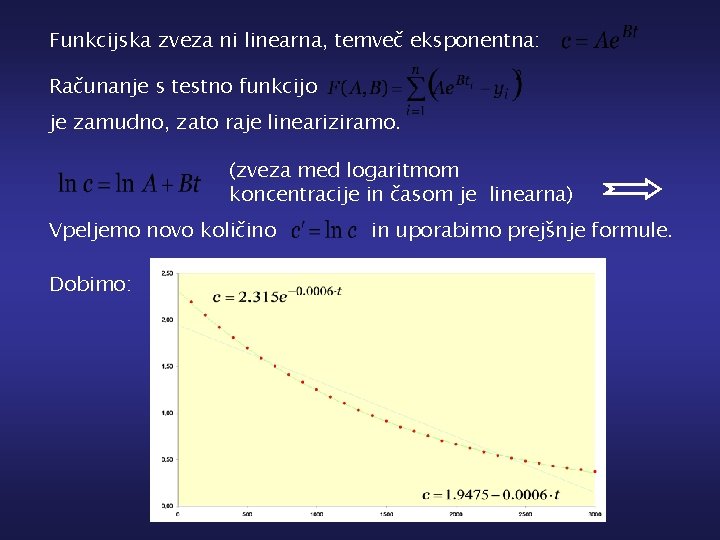
Funkcijska zveza ni linearna, temveč eksponentna: Računanje s testno funkcijo je zamudno, zato raje lineariziramo. (zveza med logaritmom koncentracije in časom je linearna) Vpeljemo novo količino Dobimo: in uporabimo prejšnje formule.

Računanje limit Računamo pri pogoju (Nedoločena oblika Velja: L’Hospitalovo pravilo )

Primeri: L’Hospitalovo pravilo uporabimo tudi za in ko je

Risanje grafov (Območje definicije, obnašanje na robu, ničle, območja naraščanja in padanja, stacionarne točke, ukrivljenost, prevoji, simetrije. ) 1. Definicijsko območje: določimo na podlagi lastnosti osnovnih funkcij. 2. Rob definicijskega območja: obnašanje funkcije (pole, asimptote) izrazimo s pomočjo limit; pri računanju si pomagamo z L’Hospitalovim pravilom. 3. Ničle: določimo s pomočjo raznih, tudi približnih, metod za reševanje enačb.

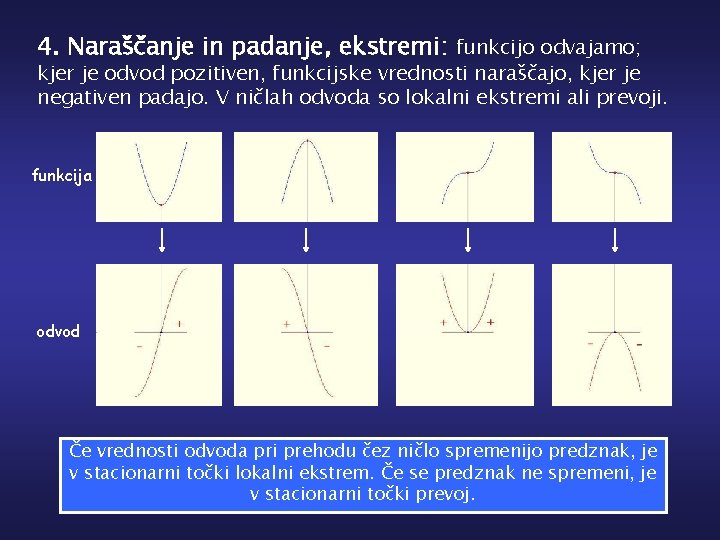
4. Naraščanje in padanje, ekstremi: funkcijo odvajamo; kjer je odvod pozitiven, funkcijske vrednosti naraščajo, kjer je negativen padajo. V ničlah odvoda so lokalni ekstremi ali prevoji. funkcija odvod Če vrednosti odvoda pri prehodu čez ničlo spremenijo predznak, je v stacionarni točki lokalni ekstrem. Če se predznak ne spremeni, je v stacionarni točki prevoj.

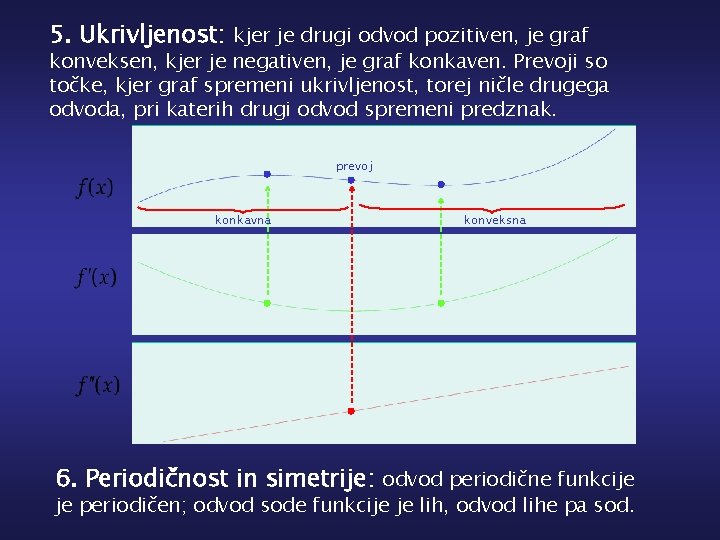
5. Ukrivljenost: kjer je drugi odvod pozitiven, je graf konveksen, kjer je negativen, je graf konkaven. Prevoji so točke, kjer graf spremeni ukrivljenost, torej ničle drugega odvoda, pri katerih drugi odvod spremeni predznak. prevoj konkavna konveksna 6. Periodičnost in simetrije: odvod periodične funkcije je periodičen; odvod sode funkcije je lih, odvod lihe pa sod.

Primeri Natančno nariši graf funkcije Definicijsko območje: imenovalec je pozitiven, funkcija je definirana povsod. Obnašanje na robu: f(x) ima vodoravno asimptoto y=0 Ničle: edina ničla števca je x=0. Simetrije: funkcija je liha.

Naraščanje, padanje, ekstremi: Ničli odvoda sta -1 in +1; odvod je negativen za x<-1 in x>1 in pozitiven za -1<x<1. Ukrivljenost: f ima prevoje za konveksna je za konkavna je za f narašča za -1<x<1 in pada sicer; v -1 ima lokalni minimum, v 1 pa lokalni maksimum.

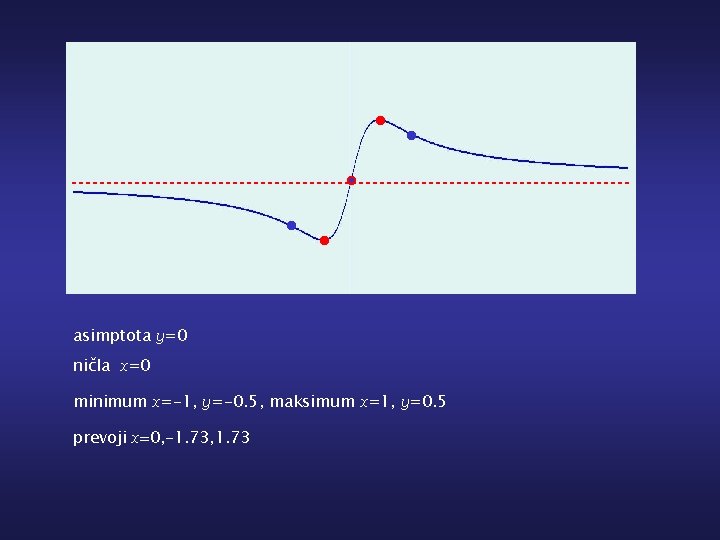
asimptota y=0 ničla x=0 minimum x=-1, y=-0. 5, maksimum x=1, y=0. 5 prevoji x=0, -1. 73, 1. 73

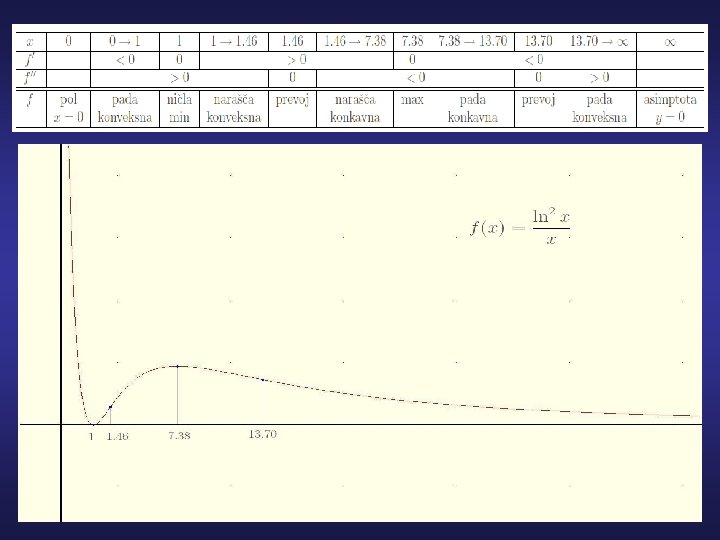
Nariši graf Definicijsko območje: navpična asimptota (pol) x=0 vodoravna asimptota y=0 Ničle funkcije, 1. in 2. odvoda: (numerično)