KVADRATNA FUNKCIJA Kvadratna funkcija je oblika gde je

KVADRATNA FUNKCIJA

Kvadratna funkcija je oblika: gde je �� ∊ℝ, a≠ 0 i a, b, c∊ℝ. Kriva u ravni koja predstavlja grafik funkcije je parabola.

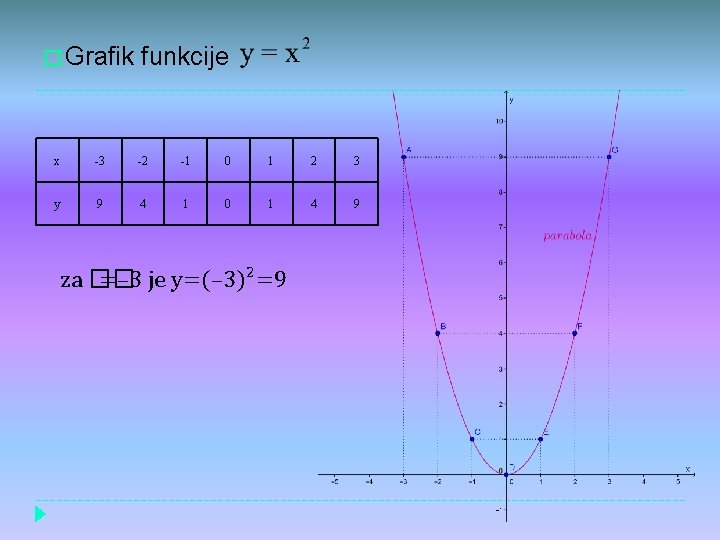
� Grafik funkcije x -3 -2 -1 0 1 2 3 y 9 4 1 0 1 4 9 za �� =– 3 je y=(– 3)²=9

� Grafik funkcije Razlikovaćemo 2 situacije: a>0 i a<0. 1. Za a>0 je parabola okrenuta „otvorom nagore”. a>0 a) a>1 U odnosu na početni grafik y=x² , ovaj grafik y=ax² se „sužava”. b) 0<a<1 U odnosu na početni grafik y=x², ovaj grafik y=ax² se „širi”.

Grafik funkcije 2. Za a<0 je parabola okrenuta „otvorom nadole”. a<0 Početni grafik je y=–x² a) a<– 1 U odnosu na početni grafik y=–x² , ovaj grafik y=ax² se „sužava”. b) – 1<a<0 U odnosu na početni grafik y=–x², ovaj grafik y=ax² se „širi”.

� Grafik funkcije → Prvo nacrtamo grafik funkcije y=ax² → taj grafik pomeramo duž y-ose i to: 1. β>0 Ako je pozitivan „podižemo” grafik, odnosno pomeramo ga u pozitivnom smeru y-ose. 2. β<0 Ako je negativan, „spuštamo” grafik, odnosno pomeramo ga u negativnom smeru y-ose. Pogledaj video.

� Grafik funkcije → Prvo nacrtamo grafik funkcije y=ax² → taj grafik pomeramo duž x-ose i to: 1. α>0 Ako je to znači da funkciju pomeramo za po x-osi udesno. 2. α<0 Ako je to znači da finkciju pomeramo za po x-osi ulevo. Pogledaj video.

� Grafik funkcije Najpre moramo funkciju svesti na takozvani kanonski oblik. Tu nam pomaže formula: ili ako uvedemo da je: i dobijamo: kanonski oblik. Tačka T(α, β) je teme parabole.

� Postupak je: → Datu funkciju y=ax²+bx+c najpre svedemo na kanonski oblik y=a(x-α)²+β → Nacrtamo grafik funkcije y=ax² → Izvršimo pomeranje (transliranje) duž x–ose za α → Izvršimo pomeranje (transliranje) duž y-ose za β

� Primer 1: Nacrtati grafik funkcije � Rešenje:

vršimo pomeranje za 3 udesno

grafik y=(x-3)² spustimo za 4 „nadole”

� Primer 2: Nacrtati grafik funkcije � Rešenje:

vršimo pomeranje za 2 ulevo grafik y=-(x+2)² spustimo za 3 „nadole”

Tok i grafik kvadratne funkcije � Ispituje se u 8 tačaka: 1. 2. 3. 4. 5. 6. 7. 8. Domen (oblast definisanosti) Nule kvadratne funkcije Presek sa y-osom Ekstremne vrednosti Monotonost Znak kvadratne funkcije Grafik funkcije Kodomen (oblast vrednosti)

1. Oblast definisanosti - Domen �Domen kvadratne funkcije je skup svih realnih brojeva. �Pišemo: �� ƒ=ℝ ili �� ∊(−∞, +∞)

2. Nule kvadratne funkcije � Nule kvadratne funkcije su realna rešenja kvadratne jednačine q Kako? � Nule funkcije su presek grafika te funkcije sa x-osom � Označimo ih sa:

2. Nule kvadratne funkcije

3. Presek sa y-osom �Presek kvadratne funkcije sa y-osom dobijamo kada u jednačini uvrstimo x=0 �Dobijemo da je presek u tački A(0, c) q Kako?

4. Ekstremne vrednosti � Kvadratna funkcija ima jednu ekstremnu vrednost i to je teme T: � Ako je a>0 imamo minimum, a ako je a<0 imamo maksimum

5. Monotonost �U zavisnosti od vrednosti koeficijenata a razlikujemo dva slučaja: 1) a>0 2) a<0

6. Znak kvadratne funkcije � U zavisnosti od vrednosti koeficijenata a i diskriminante D razlikujemo slučajeve:

7. Grafik funkcije � Grafik kvadratne funkcije je kriva koje se zove parabola

8. Oblast vrednosti - Kodomen � Kodomen funkcije je skup svih vrednosti te funkcije � Označimo sa � Ako je a>0 tada: � Ako je a<0 tada: