Lecture 8 Periodic Structures Image Parameter Method Insertion





























































- Slides: 81

Lecture 8 Periodic Structures Image Parameter Method Insertion Loss Method Filter Transformation EE 41139 Microwave Technique 1

Periodic Structures periodic structures have passband stopband characteristics and can be employed as filters EE 41139 Microwave Technique 2

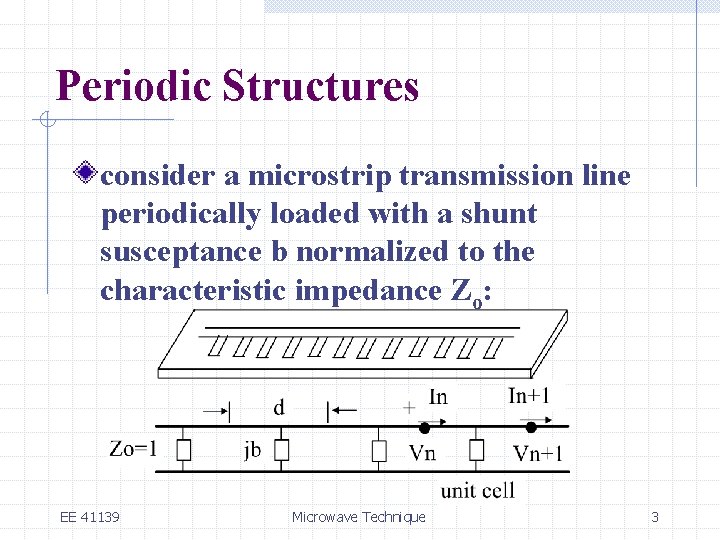
Periodic Structures consider a microstrip transmission line periodically loaded with a shunt susceptance b normalized to the characteristic impedance Zo: EE 41139 Microwave Technique 3

Periodic Structures the ABCD matrix is composed by cascading three matrices, two for the transmission lines of length d/2 each and one for the shunt susceptance, EE 41139 Microwave Technique 4

Periodic Structures i. e. EE 41139 Microwave Technique 5

Periodic Structures q = kd, and k is the propagation constant of the unloaded line AD-BC = 1 for reciprocal networks assuming the propagation constant of the loaded line is denoted by g, then EE 41139 Microwave Technique 6

Periodic Structures therefore, or EE 41139 Microwave Technique 7

Periodic Structures for a nontrivial solution, the determinant of the matrix must vanish leading to recall that AD-CB = 0 for a reciprocal network, then Or EE 41139 Microwave Technique 8

Periodic Structures Knowing that, the above equation can be written as since the right-hand side is always real, therefore, either a or b is zero, but not both EE 41139 Microwave Technique 9

Periodic Structures if a=0, we have a passband, b can be obtained from the solution to if the magnitude of the rhs is less than 1 EE 41139 Microwave Technique 10

Periodic Structures if b=0, we have a stopband, a can be obtained from the solution to as cosh function is always larger than 1, a is positive forward going wave and is negative for the backward going wave EE 41139 Microwave Technique 11

Periodic Structures therefore, depending on the frequency, the periodic structure will exhibit either a passband or a stopband EE 41139 Microwave Technique 12

Periodic Structures the characteristic impedance of the load line is given by , + forward wave and - for backward wavehere the unit cell is symmetric so that A=D ZB is real for the passband imaginary for the stopband EE 41139 Microwave Technique 13

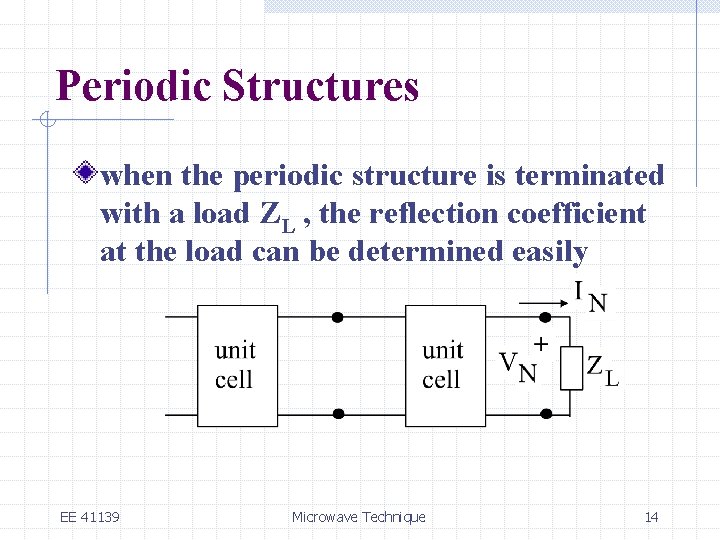
Periodic Structures when the periodic structure is terminated with a load ZL , the reflection coefficient at the load can be determined easily EE 41139 Microwave Technique 14

Periodic Structures Which is the usual result EE 41139 Microwave Technique 15

Periodic Structures it is useful to look at the k-b diagram (Brillouin) of the periodic structure EE 41139 Microwave Technique 16

Periodic Structures in the region where b < k, it is a slow wave structure, the phase velocity is slow down in certain device so that microwave signal can interacts with electron beam more efficiently when b = k, we have a TEM line EE 41139 Microwave Technique 17

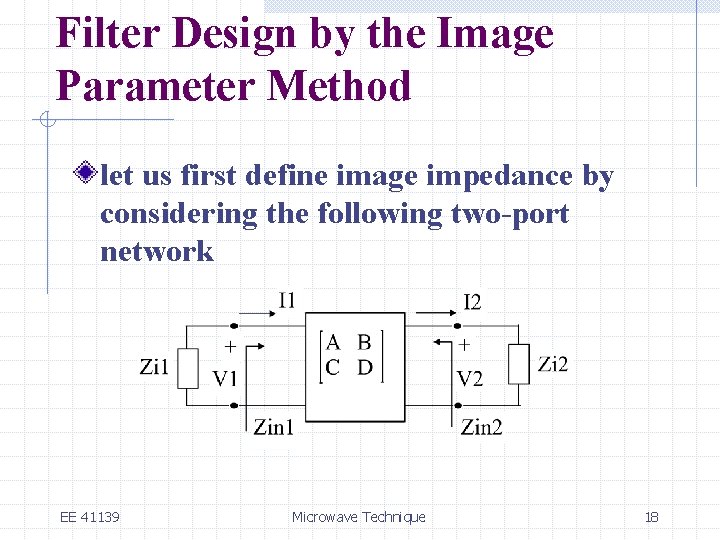
Filter Design by the Image Parameter Method let us first define image impedance by considering the following two-port network EE 41139 Microwave Technique 18

Filter Design by the Image Parameter Method if Port 2 is terminated with Zi 2, the input impedance at Port 1 is Zi 1 if Port 1 is terminated with Zi 1, the input impedance at Port 2 is Zi 2 both ports are terminated with matched loads EE 41139 Microwave Technique 19

Filter Design by the Image Parameter Method at Port 1, the port voltage and current are related as the input impedance at Port 1, with Port 2 terminated in , is EE 41139 Microwave Technique 20

Filter Design by the Image Parameter Method similarly, at Port 2, we have these are obtained by taking the inverse of the ABCD matrix knowing that AB-CD=1 the input impedance at Port 2, with Port 1 terminated in , is EE 41139 Microwave Technique 21

Filter Design by the Image Parameter Method Given and , we have , , if the network is symmetric, i. e. , A = D, then EE 41139 Microwave Technique 22

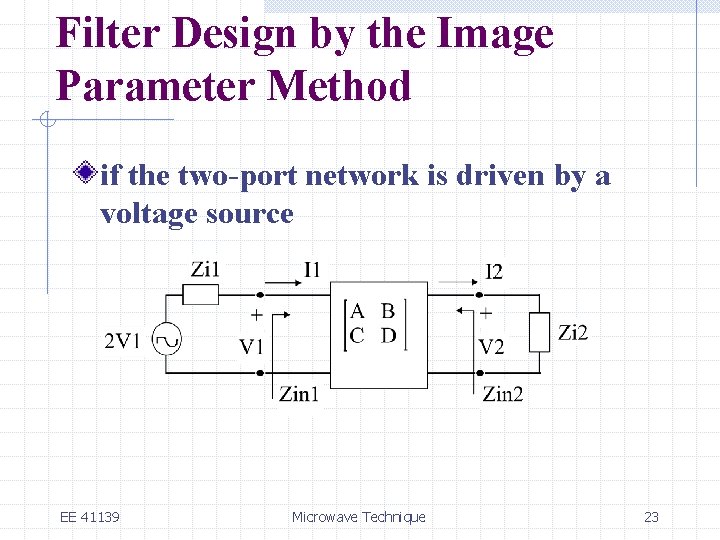
Filter Design by the Image Parameter Method if the two-port network is driven by a voltage source EE 41139 Microwave Technique 23

Filter Design by the Image Parameter Method Similarly we have, A = D for symmetric network Define EE 41139 , , Microwave Technique 24

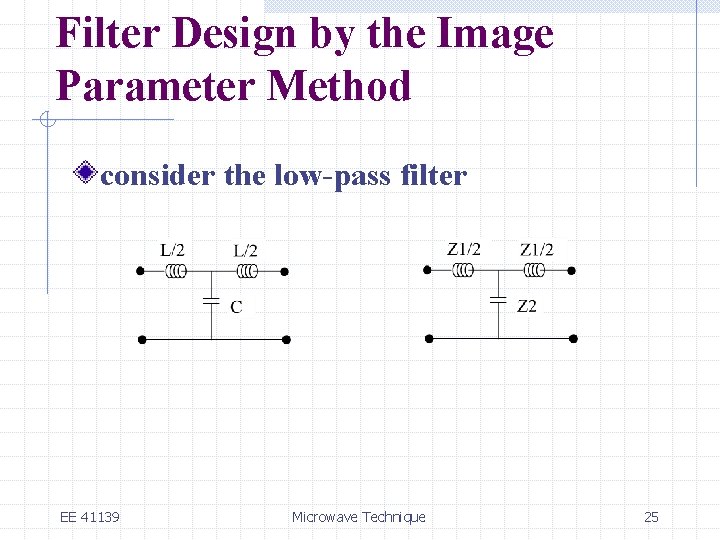
Filter Design by the Image Parameter Method consider the low-pass filter EE 41139 Microwave Technique 25

Filter Design by the Image Parameter Method the series inductors and shunt capacitor will block high-frequency signals a high-pass filter can be obtained by replacing L/2 by 2 C and C by L in Tnetwork EE 41139 Microwave Technique 26

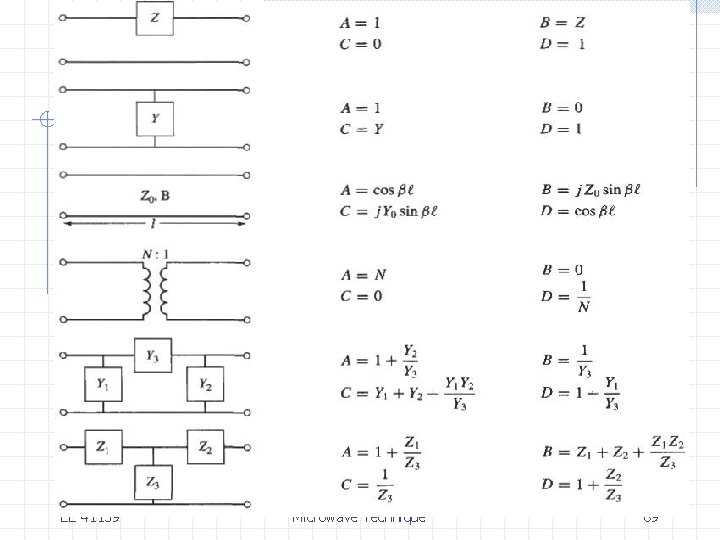
Filter Design by the Image Parameter Method the ABCD matrix is given by Image impedance EE 41139 Microwave Technique 27

Filter Design by the Image Parameter Method Propagation constant For the above T-network, EE 41139 Microwave Technique 28

Filter Design by the Image Parameter Method Define a cutoff frequency as, a nominal characteristic impedance Ro , k is a constant EE 41139 Microwave Technique 29

Filter Design by the Image Parameter Method the image impedance is then written as the propagation factor is given as EE 41139 Microwave Technique 30

Filter Design by the Image Parameter Method For , is real and which imply a passband For , have a stopband EE 41139 is imaginary and we Microwave Technique 31

Filter Design by the Image Parameter Method this is a constant-k low pass filter, there are two parameters to choose (L and C) which are determined by wc and Ro when , the attenuation is slow, furthermore, the image impedance is not a constant when frequency changes EE 41139 Microwave Technique 32

Filter Design by the Image Parameter Method the m-derived filter section is designed to alleviate these difficulties let us replace the impedances Z 1 with EE 41139 Microwave Technique 33

Filter Design by the Image Parameter Method we choose Z 2 so that Zi. T remains the same therefore, Z 2 is given by EE 41139 Microwave Technique 34

Filter Design by the Image Parameter Method recall that Z 1 = jw. L and Z 2 = 1/jw. C, the m-derived components are EE 41139 Microwave Technique 35

Filter Design by the Image Parameter Method the propagation factor for the m-derived section is EE 41139 Microwave Technique 36

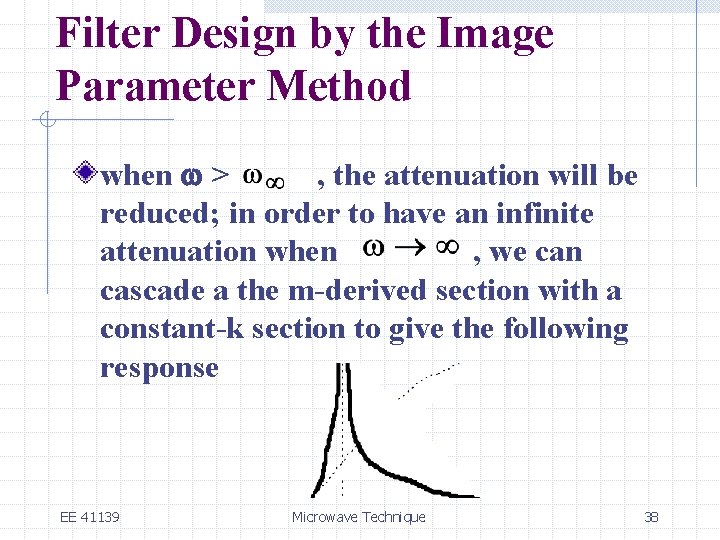
Filter Design by the Image Parameter Method if we restrict 0 < m < 1, is real and >1 , for w > the stopband begins at w = as for the constant-k section When w = , where e becomes infinity and the filter has an infinite attenuation EE 41139 Microwave Technique 37

Filter Design by the Image Parameter Method when w > , the attenuation will be reduced; in order to have an infinite attenuation when , we can cascade a the m-derived section with a constant-k section to give the following response EE 41139 Microwave Technique 38

Filter Design by the Image Parameter Method the image impedance method cannot incorporate arbitrary frequency response; filter design by the insertion loss method allows a high degree of control over the passband stopband amplitude and phase characteristics EE 41139 Microwave Technique 39

Filter Design by the Insertion Loss Method if a minimum insertion loss is most important, a binomial response can be used if a sharp cutoff is needed, a Chebyshev response is better in the insertion loss method a filter response is defined by its insertion loss or power loss ratio EE 41139 Microwave Technique 40

Filter Design by the Insertion Loss Method , IL = 10 log , , M and N are real polynomials EE 41139 Microwave Technique 41

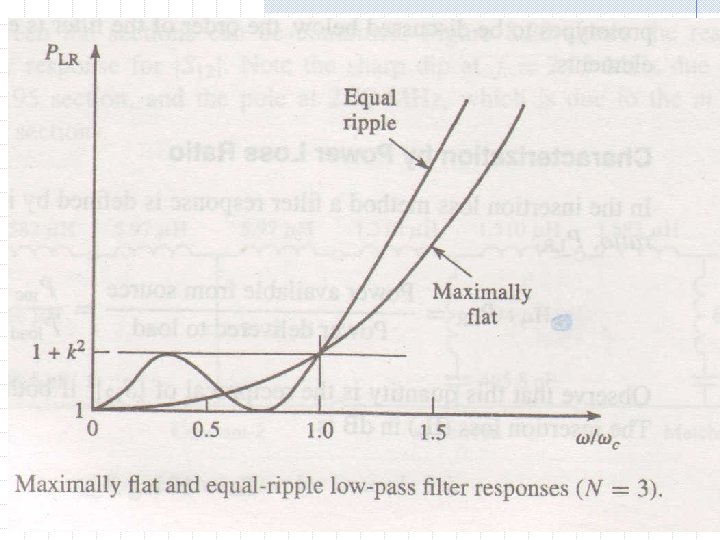
Filter Design by the Insertion Loss Method for a filter to be physically realizable, its power loss ratio must be of the form shown above maximally flat (binomial or Butterworth response) provides the flattest possible passband response for a given filter order N EE 41139 Microwave Technique 42

Filter Design by the Insertion Loss Method The passband goes from to , beyond , the attenuation increases with frequency the first (2 N-1) derivatives are zero for and for , the insertion loss increases at a rate of 20 N d. B/decade EE 41139 Microwave Technique 43

EE 41139 Microwave Technique 44

Filter Design by the Insertion Loss Method equal ripple can be achieved by using a Chebyshev polynomial to specify the insertion loss of an N-order low-pass filter as EE 41139 Microwave Technique 45

Filter Design by the Insertion Loss Method a sharper cutoff will result; (x) oscillates between -1 and 1 for |x| < 1, the passband response will have a ripple of 1+ in the amplitude For large x, and therefore for EE 41139 Microwave Technique 46

Filter Design by the Insertion Loss Method therefore, the insertion loss of the Chebyshev case is times of the binomial response for linear phase response is sometime necessary to avoid signal distortion, there is usually a tradeoff between the sharpcutoff response and linear phase response EE 41139 Microwave Technique 47

Filter Design by the Insertion Loss Method a linear phase characteristic can be achieved with the phase response EE 41139 Microwave Technique 48

Filter Design by the Insertion Loss Method a group delay is given by this is also a maximally flat function, therefore, signal distortion is reduced in the passband EE 41139 Microwave Technique 49

Filter Design by the Insertion Loss Method it is convenient to design the filter prototypes which are normalized in terms of impedance and frequency the designed prototypes will be scaled in frequency and impedance lumped-elements will be replaced by distributive elements for microwave frequency operations EE 41139 Microwave Technique 50

Insertion Loss Method

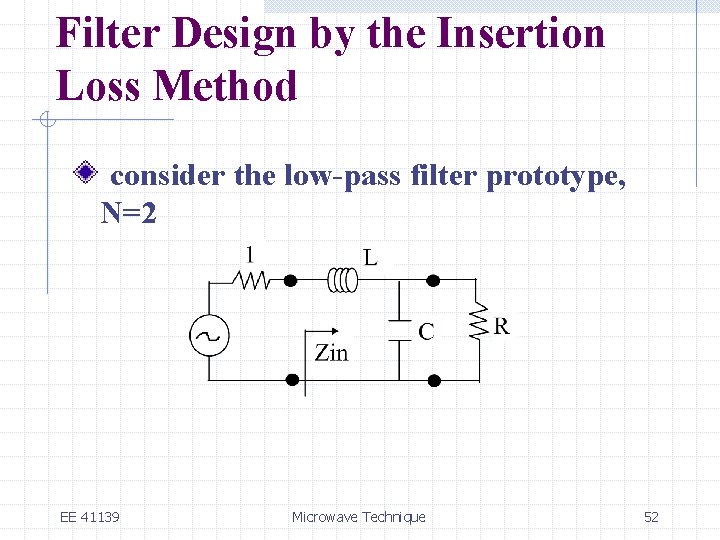
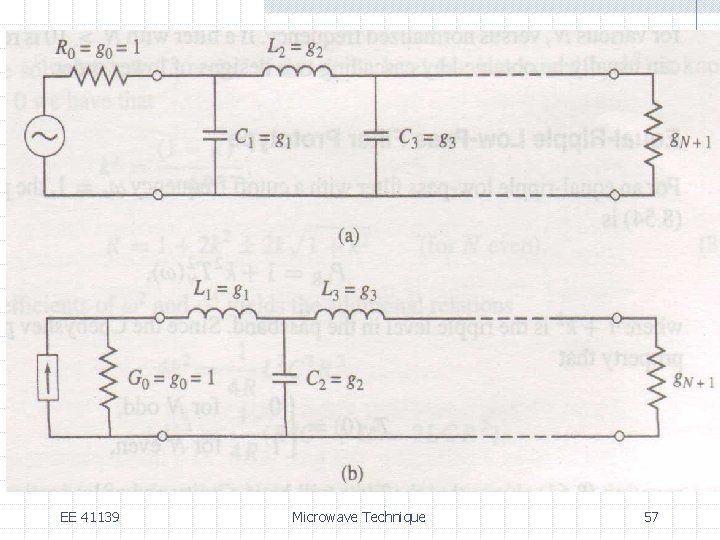
Filter Design by the Insertion Loss Method consider the low-pass filter prototype, N=2 EE 41139 Microwave Technique 52

Filter Design by the Insertion Loss Method assume a source impedance of 1 W and a cutoff frequency the input impedance is given by EE 41139 Microwave Technique 53

Filter Design by the Insertion Loss Method the reflection coefficient at the source impedance is given by the power loss ratio is given by EE 41139 Microwave Technique 54

the power loss ratio is given by EE 41139 Microwave Technique 55

Filter Design by the Insertion Loss Method compare this equation with the maximally flat equation, we have R=1, which implies C = L as R = 1 which implies C = L = EE 41139 Microwave Technique 56

EE 41139 Microwave Technique 57

Filter Design by the Insertion Loss Method for equal-ripple prototype, we have the power loss ratio Since Compare this with EE 41139 Microwave Technique 58

Filter Design by the Insertion Loss Method we have or note that R is not unity, a mismatch will result if the load is R=1; a quarter-wave transformer can be used to match the load EE 41139 Microwave Technique 59

Filter Design by the Insertion Loss Method after the filter prototypes have been designed, we need to perform impedance and frequency scaling EE 41139 Microwave Technique 60

Filter Transformations impedance and frequency scaling the impedance scaled quantities are: EE 41139 Microwave Technique 61

Filter Transformations both impedance and frequency scaling low-pass to high-pass transformation , EE 41139 Microwave Technique 62

Filter Transformations Bandpass transmission As a series indicator , is transformed into a series LC with element values A shunt capacitor, , is transformed into a shunt LC with element values 63

Filter Transformations bandstop transformation A series indicator, , is transformed into a parallel LC with element values A shunt capacitor, , is transformed into a series LC with element values EE 41139 Microwave Technique 64

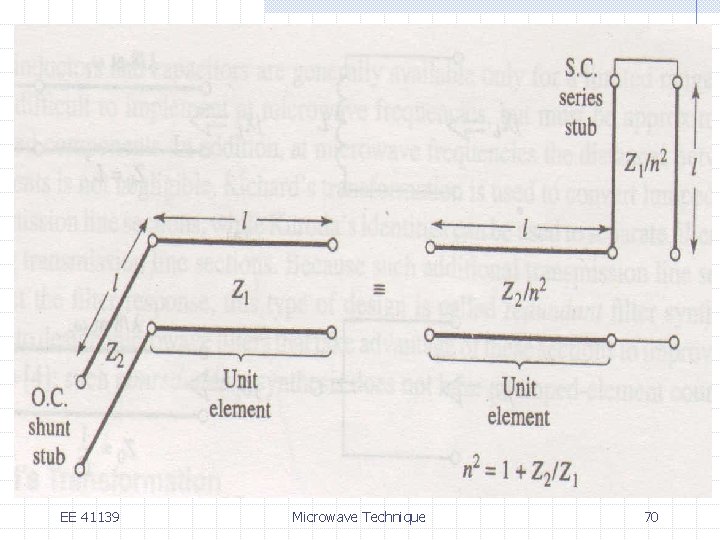
Filter Implementation we need to replace lumped-elements by distributive elements: EE 41139 Microwave Technique 65

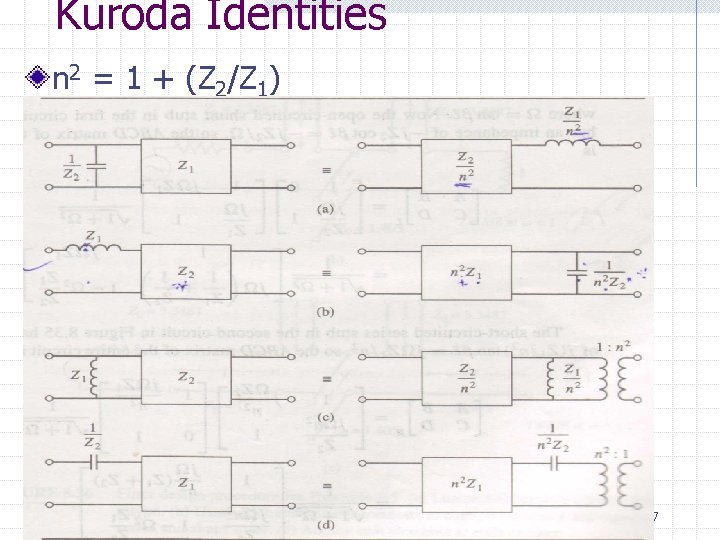
Filter Implementation there are four Kuroda identities to perform any of the following operations: n n n EE 41139 physically separate transmission line stubs transform series stubs into shunt stubs, or vice versa change impractical characteristic impedances into more realizable ones Microwave Technique 66

Kuroda Identities n 2 = 1 + (Z 2/Z 1) EE 41139 Microwave Technique 67

The inductors and capacitors represent shortcircuit and open-circuit stubs respectively. EE 41139 Microwave Technique 68

EE 41139 Microwave Technique 69

EE 41139 Microwave Technique 70

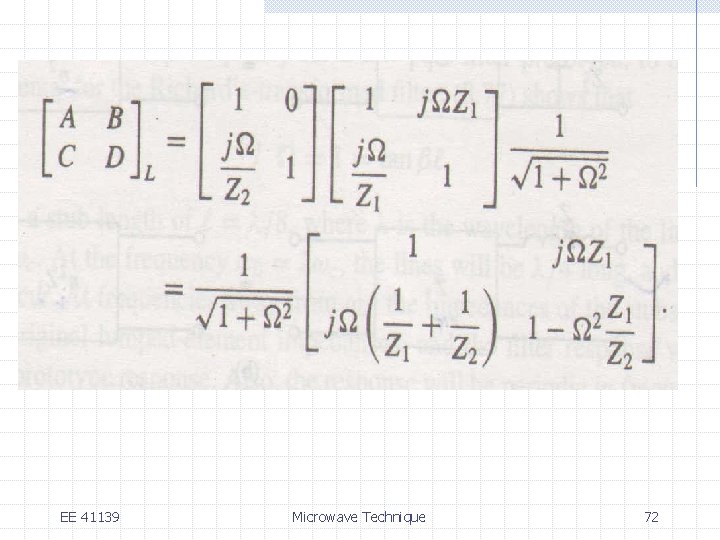
The O. C shunt stub in the first circuit has an impedance of So the ABCD matrix of the entire circuit is EE 41139 Microwave Technique 71

EE 41139 Microwave Technique 72

The S. C series stub in the second circuit has an impedance of So the ABCD matrix of the entire circuit is EE 41139 Microwave Technique 73

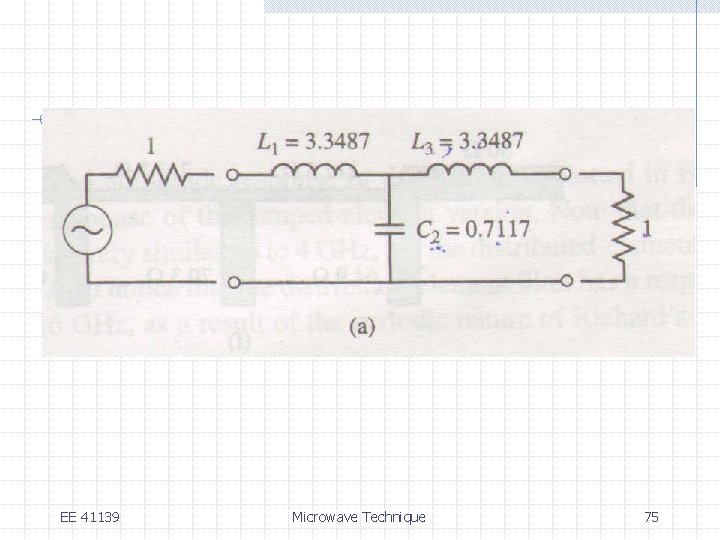
EE 41139 Microwave Technique 74

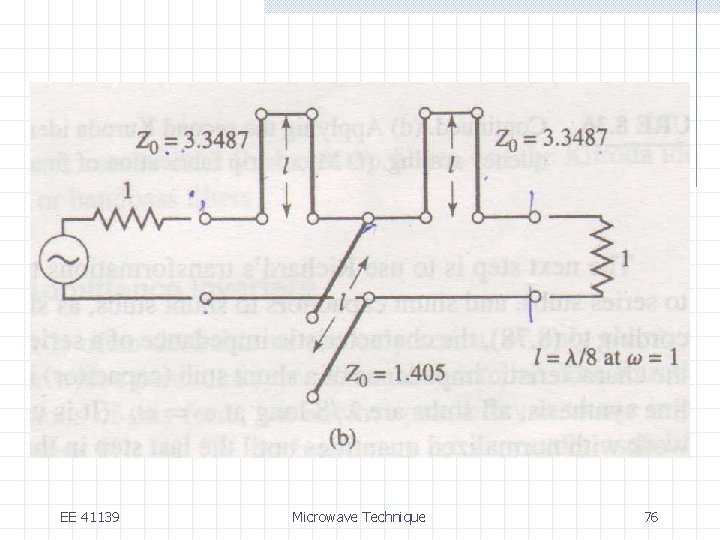
EE 41139 Microwave Technique 75

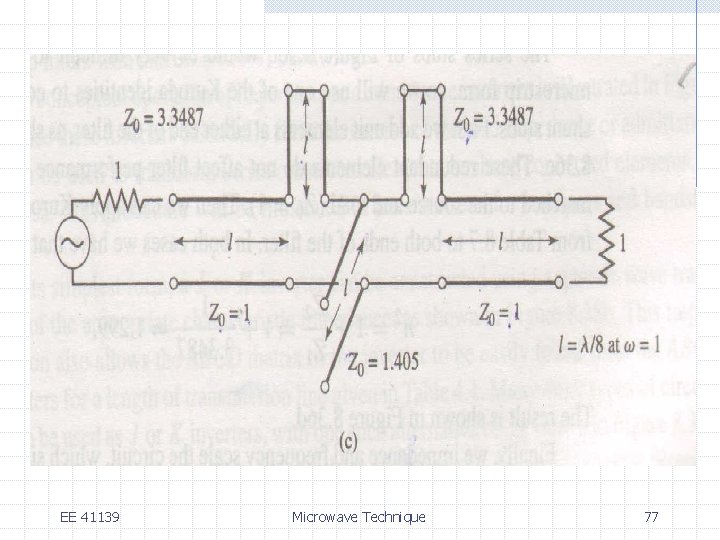
EE 41139 Microwave Technique 76

EE 41139 Microwave Technique 77

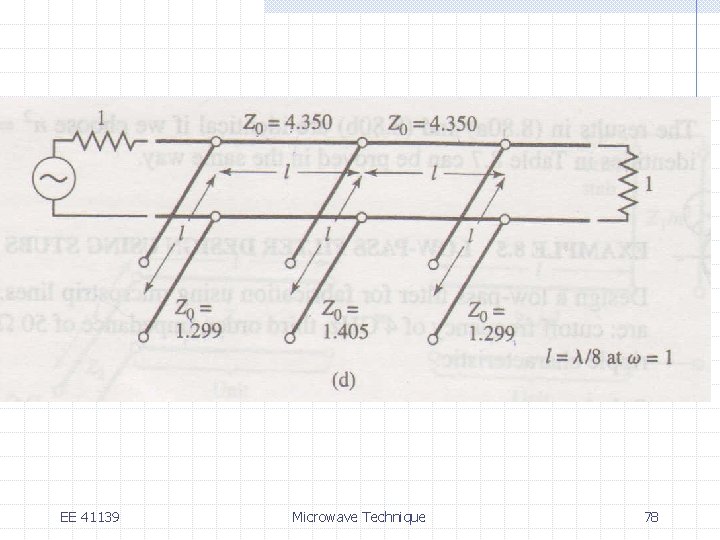
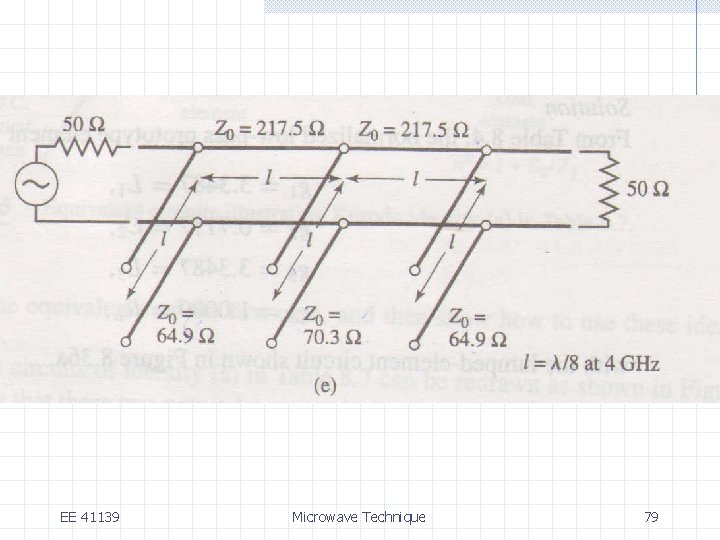
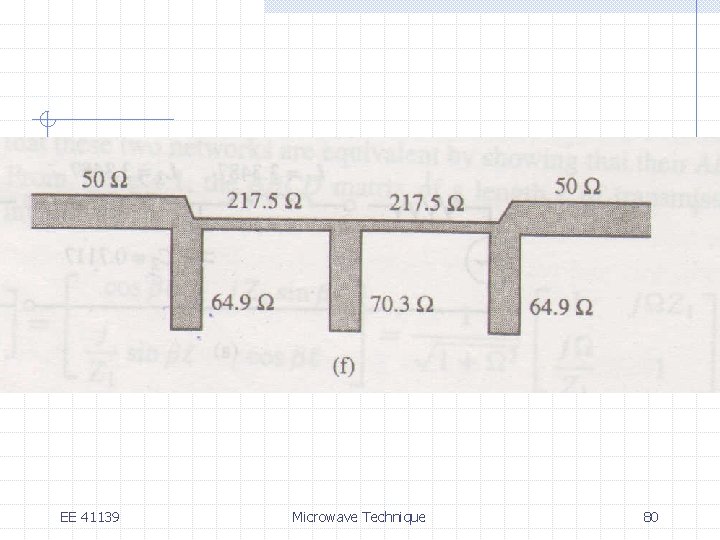
EE 41139 Microwave Technique 78

EE 41139 Microwave Technique 79

EE 41139 Microwave Technique 80

EE 41139 Microwave Technique 81
 Image parameter method
Image parameter method 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Analogous structure
Analogous structure Chapter 6 the periodic table
Chapter 6 the periodic table Atomic trends
Atomic trends Boron group number
Boron group number 6 the periodic table
6 the periodic table The periodic table and periodic law chapter 6
The periodic table and periodic law chapter 6 Image processing lecture notes
Image processing lecture notes Euclidean transformation in digital image processing
Euclidean transformation in digital image processing Purpose of symposium
Purpose of symposium Global stiffness matrix
Global stiffness matrix Comparative education definition
Comparative education definition Definition of teaching method
Definition of teaching method Hamza kashgari
Hamza kashgari Real image vs virtual image
Real image vs virtual image Real vs virtual images
Real vs virtual images Translate
Translate What is image restoration in digital image processing
What is image restoration in digital image processing Arithmetic coding in digital image processing
Arithmetic coding in digital image processing Image segmentation in digital image processing
Image segmentation in digital image processing Analog image and digital image
Analog image and digital image Huffman coding example
Huffman coding example Image sharpening and restoration
Image sharpening and restoration Motion segmentation
Motion segmentation Image geometry in digital image processing
Image geometry in digital image processing Area of convergence
Area of convergence Zooming and shrinking in digital image processing
Zooming and shrinking in digital image processing Ce n'est pas une image juste c'est juste une image
Ce n'est pas une image juste c'est juste une image Difference between logical file and physical file
Difference between logical file and physical file Resultado
Resultado Cameraman.tif
Cameraman.tif Image transforms in digital image processing
Image transforms in digital image processing Maketform matlab
Maketform matlab Noise
Noise Xuite blog
Xuite blog Generative adversarial networks
Generative adversarial networks Time parameter in jcl
Time parameter in jcl Parameter (informatik)
Parameter (informatik) Hur kontrollerar du de vitala parametrarna
Hur kontrollerar du de vitala parametrarna Contoh estimasi parameter
Contoh estimasi parameter Revit built in parameter
Revit built in parameter Parameters asl
Parameters asl Gambar struktur kristal
Gambar struktur kristal Parameter fisik fluida
Parameter fisik fluida Stir shaken verstat
Stir shaken verstat Statistic vs parameter example
Statistic vs parameter example Whats a parameter in stats
Whats a parameter in stats Sampling distribution sample mean
Sampling distribution sample mean Proboyo
Proboyo Pengertian pendugaan parameter
Pengertian pendugaan parameter Jenis pendugaan parameter
Jenis pendugaan parameter Pendugaan rasio dua ragam
Pendugaan rasio dua ragam Contoh soal penaksiran parameter
Contoh soal penaksiran parameter Readonly struct
Readonly struct Kriteria kesehatan lingkungan
Kriteria kesehatan lingkungan Laju pertumbuhan intrinsik
Laju pertumbuhan intrinsik Parameter fisik kualitas air
Parameter fisik kualitas air Bayesian estimation
Bayesian estimation Population of interest
Population of interest Variation in mathematics
Variation in mathematics Jenis passing parameter
Jenis passing parameter Musikalische parameter
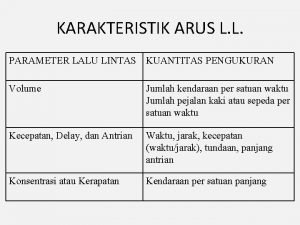
Musikalische parameter Parameter lalu lintas
Parameter lalu lintas Weaning parameter
Weaning parameter What is parameter in programming
What is parameter in programming Fmea boundary diagram example
Fmea boundary diagram example Rumus distribusi t
Rumus distribusi t Point of estimate formula
Point of estimate formula Verilog parameters
Verilog parameters Method of variation of parameters
Method of variation of parameters Contoh soal estimasi parameter
Contoh soal estimasi parameter Parameter computer science
Parameter computer science Larson miller
Larson miller Screening business ideas positive and negative
Screening business ideas positive and negative Algoritma prosedur
Algoritma prosedur Matlab parameter estimation
Matlab parameter estimation Nomenklatur übertragungsglieder
Nomenklatur übertragungsglieder Ukuran lokasi
Ukuran lokasi Toomre q parameter
Toomre q parameter Colorize photo
Colorize photo Parameter geometrik jalan
Parameter geometrik jalan