Image Restoration The main aim of restoration is

Image Restoration • The main aim of restoration is to improve an image in some predefined way. • Image Enhancement is a subjective process whereas Image restoration tries to reconstruct or recover an image which was degraded using a priori knowledge of degradation. • Here we model the degradation and apply the inverse process to recover the original image. • Enhancement techniques take advantage of the psychophysical aspects of human visual system. • (eg) contrast stretching is an enhancement method as it is concerned with the pleasing aspects of a viewer, whereas removal of image blur is a restoration process.

Model of Image Degradation / Restoration Process • In this model, we assume that there is an additive noise term, operating on an input image f(x, y) to produce a degraded image g(x, y). • Given g(x, y) and some information about degradation function H, and knowledge about noise term η(x, y). • The aim of restoration is to get an estimate f(x, y) of original image. • The more we know about H and term η, we get better results.

Model of Image Degradation / Restoration Process • Here H is a linear, position-invariant process. The degraded image is given as: • g(x, y) = h(x, y)*f(x, y) + η(x, y) • Here h(x, y) is the spatial representation of the degradation function. • The symbol * indicates convolution. • The convolution in spatial domain is equal to multiplication in frequency domain. • In Frequency domain we have: • G(u, v) = H(u, v)F(u, v) + N(u, v) • Here capital letters are the Fourier transforms of the corresponding terms. • For simplicity, we consider the case of H being the identity operator.

Origin of Noise • Noise in a digital image arises mainly due to acquisition (digitization) and / or transmission. • Environmental conditions, quality of sensing elements, interference in the transmission channel, lightning and atmospheric disturbance are some examples.

Properties of Noise • When the Fourier spectrum of noise is constant, the noise is called a white noise. • This is similar to white light, which contains nearly all frequencies in the visible spectrum in equal quantities. • Fourier spectrum of a function containing all frequencies in equal proportions is a constant. • We assume that noise is independent of coordinates, and it is uncorrelated with respect to the pixel values.

Noise Probability Density Functions • The noise component is considered to be a random variable and characterized by a probability density function (PDF). • Some common PDFs used in image processing are: • Gaussian noise • Gaussian (or normal) noise wide spread in usage. The PDF of a Gaussian random variable, z is given by • p(z) = (1/sqrt(2*Л*σ)). exp (-(z-μ)2/2* σ2) • Here z represents gray level, μ is the mean of z, and σ is the standard deviation. • The square of standard deviation is called the variance of z. • Nearly 70% of the value of this function lies in the range [(μ – σ), (μ + σ)] and about 95% of its value lies in the range [(μ – 2 σ), (μ + 2σ)].

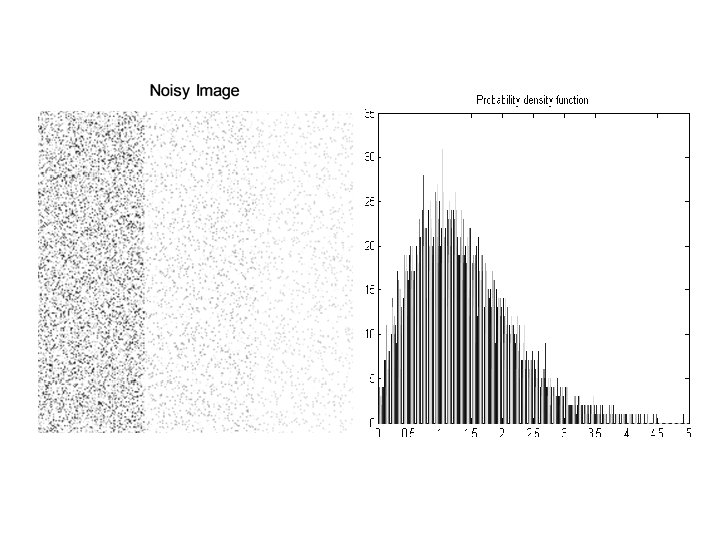
% Gaussian noise % Read a gray scale image (having few regulat patterns) and add gaussian % noise of certain mean value, standard deviation and certain percentage. % plot the histogram of noise, noisy image. ensure that the profile of the % noise is visible in the profile of the noisy image. clear all; close all; clc; a = imread('pattern. png'); a = im 2 double(a); size. A = size(a); p 3 = 0; % Gaussian noise mean value p 4 = 1; % Gaussian noise variance value R = p 3+p 4*randn([256, 256]); R 1 = a+R; figure, imshow(R 1), title('Noisy Image'); figure, hist(R, 50), title('Probability density function');

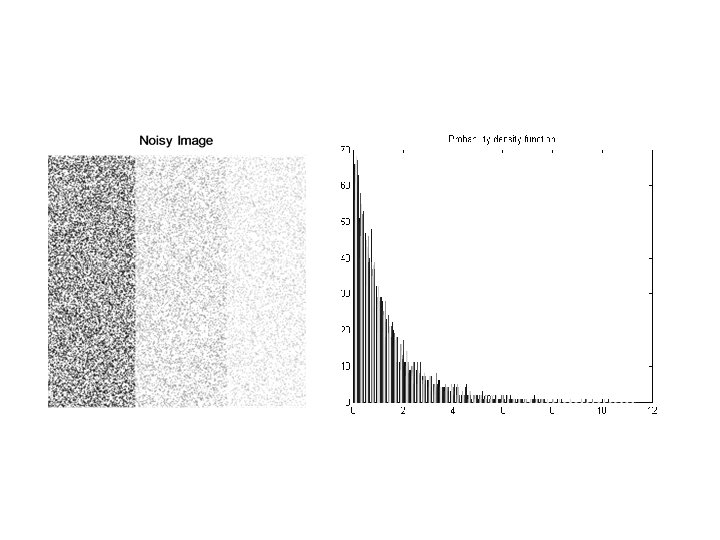
Rayleigh noise • • • The PDF of Rayleigh noise is given by p(z) = (2/b)*(z-a)*exp(-(z-a)2/b for z ≥ a = 0 for z < a The mean and variance of this PDF are: μ = a + sqrt(Πb/4) and σ2 = b(r – Π)/4. One has to note the displacement of PDF from the origin and skewed to the right. • Thus this is useful for skewed histograms.

% Rayleigh noise % Read a gray scale image (having few regulat patterns) and add rayleigh % noise of certain mean value, standard deviation and certain percentage. % plot the histogram of noise, noisy image. ensure that the profile of the % noise is visible in the profile of the noisy image. clear all; close all; clc; a = imread('pattern. png'); a = im 2 double(a); size. A = size(a); p 3 = 0. 95; A = 0; B = 2; R = A + (-B*log(1 -rand(size. A))). ^0. 5; x = rand(size. A); b=a; for i=1: size. A(1) for j=1: size. A(2) if (x(i, j)< p 3) b(i, j)=a(i, j)+R(i, j); end end figure, imshow(a); figure, imshow(b), title('Noisy Image'); figure, hist(R, 50), title('Probability density function'); figure, hist(b);

Erlang (Gamma) noise • The PDF of Erlang noise is given by • abzb-1 • p(z) = ---- e-az for z ≥ 0 • (b -1) ! • = 0 for z < 0 • Here a > 0, b is a positive integer. The mean and variance of this density are: • μ = (b/a) and σ2 = (b/a 2).

% noise of certain mean value, standard deviation and certain percentage. % plot the histogram of noise, noisy image. ensure that the profile of the % noise is visible in the profile of the noisy image. clear all; close all; clc; a = imread('pattern. png'); a = im 2 double(a); size. A = size(a); p 3 = 0. 9; A = 2; B = 5; k = -1/A; R = zeros(size. A); for i=1: B R = R+k*log(1 -rand(size. A)); end x = rand(size. A); b=a; for i=1: size. A(1) for j=1: size. A(2) if (x(i, j)< p 3) b(i, j)=a(i, j)+R(i, j); end end figure, imshow(a); figure, imshow(b), title('Noisy Image');

Exponential noise • The PDF of exponential noise is given as: • p(z) = ae-az for z ≥ 0 • = 0 for z < 0 • Here a > 0. The mean and variance of this density function are • μ = (1/a) and σ2 = (1/a 2). • This PDF is the special case of the Erlang PDF, with b =1.

% Exponential noise % Read a gray scale image (having few regulat patterns) and add exponential % noise of certain mean value, standard deviation and certain percentage. % plot the histogram of noise, noisy image. ensure that the profile of the % noise is visible in the profile of the noisy image. clear all; close all; clc; a = imread('pattern. png'); a = im 2 double(a); size. A = size(a); p 3 = 0. 9; A = 1; k = -1/A; R = k*log(1 -rand(size. A)); x = rand(size. A); b=a; for i=1: size. A(1) for j=1: size. A(2) if (x(i, j)< p 3) b(i, j)=a(i, j)+R(i, j); end end figure, imshow(a); figure, imshow(b), title('Noisy Image'); figure, hist(R, 50), title('Probability density function'); figure, hist(b);

Uniform noise • The PDF of uniform noise is given by: • p(z) = (1/(b-a)) if a ≤ z ≤ b • = 0 otherwise • The mean and variance are given as: • μ = (a+b)/2 and σ2 = ((b-a)2)/12.

% Uniform noise % Read a gray scale image (having few regulat patterns) and add uniform % noise of certain mean value, standard deviation and certain percentage. % plot the histogram of noise, noisy image. ensure that the profile of the % noise is visible in the profile of the noisy image. clear all; close all; clc; a = imread('pattern. png'); %a = zeros([256, 256]); a = im 2 double(a); size. A = size(a); A = 0; % Min noise level B = 1; % Max noise level p 3 = 0. 95; % Noise percentage R = A + (B - A)*rand(size. A); x = rand(size. A); b=a; for i=1: size. A(1) for j=1: size. A(2) if x(i, j) < p 3 b(i, j)=a(i, j)+R(i, j); end end figure, imshow(a); figure, imshow(b), title('Noisy Image'); figure, hist(R, 50), title('Probability density function'); figure, hist(b);

Impulse ( salt and pepper) noise • The PDF of (bipolar) impulse noise is given by: • p(z) = Pa for z = a • = Pb for z = b • = 0 otherwise • If b > a, gray-level b will appear as a light dot in the image. Level a will appear like a dark dot. • If either Pa or Pb is zero, the impulse noise is called unipolar. • If both the probabilities are equal, impulse noise will resemble salt and pepper noise. • Hence bipolar noise is also called as salt-andpepper noise or Shot and spike noise.

Impulse Noise • Noise impulses can be positive or negative. • Generally impulse corruption is large compared to the strength of image signal and hence are treated as extreme (black or white) values. • Negative impulses appear s black (pepper) points. • Positive impulses appear white (salt) noise. • For an 8 bit image a = 0 (black) and b = 255 (white).

% Salt & pepper noise % Read a gray scale image (having few regulat patterns) and add salt & % pepper noise of certain mean value, standard deviation and certain percentage. % plot the histogram of noise, noisy image. ensure that the profile of the % noise is visible in the profile of the noisy image. clear all; close all; clc; %a = imread('pattern. png'); a = zeros([256, 256]); a = im 2 double(a); size. A = size(a); p 3 = 0. 3; b = a; x = rand(size. A); b(x < p 3/2) = 0; % Minimum value b(x >= p 3/2 & x < p 3) = 1; % Maximum (saturated) value figure, imshow(a); figure, imshow(b), title('Noisy Image'); figure, hist(b, 50), title('Probability density function');

Origin of Noises • Gaussian noise arises in an image such as electronic circuit noise and sensor noise due to poor illumination and/or high temperature. • The Rayleigh noise arises in range imaging. • The exponential and gamma noises appear in laser imaging. • Impulse noise is found in places where quick transients, such as faulty switching take place during imaging.

Restoring Noisy images in spatial domain • Spatial filtering is good when only additive noise is present. • Arithmetic mean filter • Let Sxy represent the set of coordinates in a rectangular subimage window of size m X n, centered at (x, y). • The arithmetic mean filter computes the average value of the corrupted image g(x, y) in the area of Sxy. • The restored image f’ at any point (x, y) is the arithmetic mean calculated using the region of Sxy. Thus, • f’(x, y) = (1/mn) * Σ g(s, t) • This operation is carried on a convolution mask in which all coefficients have the value (1/mn). • This filter simply smoothes local variations in an image. • Noise is reduce as a result of blurring.

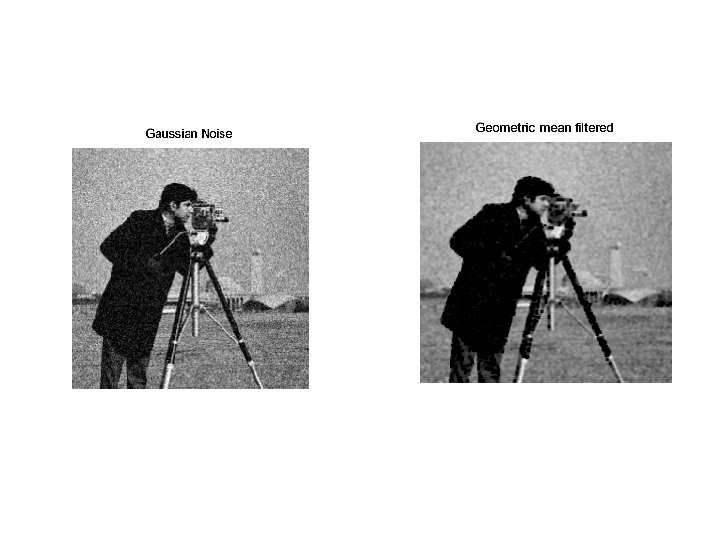
Geometric mean filter • This filter can be implemented using the expression: • f’(x, y) = [ Π g(s, t) ]1/mn • Here each restored pixel is given by the product of the pixels in the subimage window, raised to the power of 1/mn. • It gives smoothing comparable to that of arithmetic mean filter, but tends to lose less image detail during the process.

Harmonic mean filter • • • This filter can be given by: f’(x, y) = (mn) / Σ (1/g(s, t)). This filter is good for removing salt noise. But fails to remove pepper noise. It works well with other noises such as Gaussian noise.

% Harmonic mean filter % Read a gray scale image and add a noise to it and filter it using % Harmonic mean filter. clear all; close all; clc; f = imread('Saltcman. tif'); %f = imnoise(f, 'gaussian', 0, 0. 02); f = im 2 double(f); %subplot(1, 2, 1), imshow(f), title('Original Image'); figure, imshow(f), title('Salt Noise'); [m n]=size(f); for i = 2: m-1 for j = 2: n-1 con=0; s 1=0; for k 1 = i-1: i+1 for p 1 = j-1: j+1 con = con+1; if f(k 1, p 1)==0 s 1 = s 1+0; else s 1=s 1+(1/f(k 1, p 1)); end end b 1(i, j)=con/s 1; end %subplot(1, 2, 2), imshow(b 1), title('Harmonic mean filtered'); figure, imshow(b 1), title('Harmonic mean filtered');

Contra harmonic mean filter • This filer can be implemented using the expression: • f’(x, y) = Σ g(s, t)Q+1/Σ g(s, t)Q • Here Q is the order of the filter. • It is good for reducing the effect of salt and pepper noise. • For positive values of Q, it eliminates pepper noise and for negative values of Q it eliminates salt noise. • It reduces to arithmetic mean filter for Q = 0 and harmonic mean filter for Q = -1. • Generally, the positive order filter cleans the background, by blurring dark areas.

Contra harmonic mean filter • Arithmetic and geometric mean filters are good for removing random noise like Gaussian or uniform noise. • Contraharmonic filer is good for impulse noise. • But it must be known before hand that whether the noise is dark or light to fix the Q value.

% Contraharmonic mean filter % Read a gray scale image and applay contraharmonic filter for verious Q % values. prove that for negative values of Q salt noise is removed, for % positive values of Q pepper noise is removed. check that % for Q=0 it becomes mean filter and for Q=-1 it becomes harmonic filter. clear all; close all; clc; f = imread('Peppercman. tif'); %f = imnoise(f, 'salt & pepper', 0. 1); f = im 2 double(f); %subplot(1, 2, 1), imshow(f), title('Original Image'); figure, imshow(f), title('Pepper Noise'); [m n]=size(f); Q=1; for i = 2: m-1 for j = 2: n-1 con=0; s 1=0; s 2=0; for k 1 = i-1: i+1 for p 1 = j-1: j+1 con = con+1; s 1=s 1+(f(k 1, p 1)^Q); s 2=s 2+(f(k 1, p 1)^(Q+1)); end b 1(i, j)=s 2/s 1; end %subplot(1, 2, 2), imshow(b 1), title('Cantraharmonic mean filtered'); figure, imshow(b 1), title('Contraharmonic mean filtered');

Order Statistics Filter • These are spatial filters whose response is based on ordering (ranking) the pixels in the image area encompassed by the filter. • Median filter • Here we replace the value of a pixel by the median of the gray values in the neighborhood of that pixel: • f’(x, y) = median {g(s, t)} • The original value of the pixel is included in the calculation of the median. • For some types of random noise, they give excellent noise-reduction with less blurring than linear smoothing filters of same size. • They work well with unipolar and bipolar impulse noises.

Max and min filters • Median is the 50 th percentile of a ranked set of numbers. The 100 th percentile results in max filter given as: • f’(x, y) = max {g(s, t)} • This filter is useful in finding the brightest spots in an image. • As pepper noise has very low intensity values, they are reduced by this filter. • The 0 th percentile filter is the min filter: • f’(x, y) = min {g(s, t)} • this filter is capable of identifying the darkest points in an image. • It reducecs salt noise as a result of min operation.

% Max and Min filters % Read a gray scale image and add salt & pepper noise and remove the same % with min filter and max filter. clear all; close all; clc; f = imread('cameraman. tif'); f = imnoise(f, 'salt & pepper', 0. 01); f = im 2 double(f); %subplot(2, 2, 1), imshow(f), title('Original Image'); figure, imshow(f), title('Noisy Image'); [m n]=size(f); Q=0; for i = 2: m-1 for j = 1: n-1 con=0; for k 1 = i-1: i+1 for p 1 = j-1: j+1 con = con+1; s 1(con)=(f(k 1, p 1)); end b 1(i, j)=min(s 1); b 2(i, j)=max(s 1); end %subplot(2, 2, 2), imshow(b 1), title('Min filter'); %subplot(2, 2, 3), imshow(b 2), title('Max filter'); figure, imshow(b 1), title('Min filter'); figure, imshow(b 2), title('Max filter');

Midpoint filter • This filter is simply the midpoint between the maximum and minimum values in the area enclosed by the filter: • f’(x, y) = (1/2) * [ max {g(s, t)} + min {g(s, t)}] • This filter combines order statistic and averaging. • It is good for randomly distributed noise, like Gaussian or uniform noise.

% Midpoint filter % Read a gray scale image and add gaussian noise and remove the noise using % midpoint filter clear all; close all; clc; f = imread('cameraman. tif'); f = imnoise(f, 'gaussian', 0, 0. 01); f = im 2 double(f); %subplot(1, 2, 1), imshow(f), title('Noisy Image'); figure, imshow(f), title('Noisy Image'); [m n]=size(f); Q=0; for i = 2: m-1 for j = 2: n-1 con=0; for k 1 = i-1: i+1 for p 1 = j-1: j+1 con = con+1; s 1(con)=(f(k 1, p 1)); end b 1=min(s 1); b 2=max(s 1); R_img(i, j)=(b 1+b 2)/2; end %subplot(1, 2, 2), imshow(R_img), title('Midpoint filtered'); figure, imshow(R_img), title('Midpoint filtered');

Alpha trimmed mean filter • Let us delete the d/2 lowest and the d/2 highest gray -level values of g(s, t) in the neighborhood of Sxy. • Let gr(s, t) represent the remaining (mn – d ) pixels. • A filter formed by averaging these remaining pixels is called an alpha-trimmed mean filter: • f’(x, y) = (1/(mn-d))* Σ gr(s, t) • Here the value of d can vary from 0 to (mn – 1). • When d = 0, it reduces to arithmetic mean filter. • For d = (mn-1)/2, it becomes a median filter. • For other values of d, it is useful in situations involving multiple types of noise, such as combination of salt and pepper and Gaussian noise.

% trimed mean filter. prove that for D=0 it becomes arithmetic mean filter % and for d=(mn-1)/2 it becomes median filter. show that this filter % removes combination of gaussian and salt & pepper noise. clear all; close all; clc; f = imread('cameraman. tif'); f = im 2 double(f); f = imnoise(f, 'salt & pepper', 0. 1); f = imnoise(f, 'gaussian', 0, 0. 01); [m n]=size(f); f 1=zeros(m, n); D = 4; d = D/2; for i=3: m-2 for j=3: n-2 con=0; for k=i-2: i+2 for p=j-2: j+2 con=con+1; s(con)=f(k, p); end s = sort(s); r = (size(s, 2)-d); s 1= s(d+1: r); f 1(i, j)= sum(s 1)/(con-D); end figure, imshow(f), title('Noisy Image');

Adaptive filters • The filters discussed above, do not worry about the image characteristics. • Adaptive filters are one whose behavior changes based on statistical characteristics of the image inside the filter region defined by the m X n subimage. • Adaptive, local noise reduction filter • Mean and variance are the simple statistical feature of a random variable. • They are related to the appearance of an image. • Mean gives a measure of average gray level in the region over which the mean is computed and variance gives a measure of average contrast in that region.

Response of a filter • The response of a filter at (x, y) depends on: • g(x, y), the value of the noisy image at (x, y). • ση 2, the variance of the noise corrupting the image f(x, y) • m. L, the local mean of the pixels in Sxy. • σL 2, the local variance of the pixels in Sxy.

Behavior of a filter • The filter should behave as follows: • If ση 2 is zero, filter should return the value of g(x, y). • If local variance is high relative to ση 2, the filter should return a value close to g(x, y). • A high local variance is related with edges, and should be preserved. • If the 2 variances are equal, the filter should return the arithmetic mean value of the pixels in Sxy.

Behavior of a filter • An adaptive expression for obtaining f’(x, y) based on these assumptions is given as: • f’(x, y) = g(x, y) – (ση 2 / σL 2) * [g(x, y) – m. L] • One needs to know or estimate the variance of overall noise ση 2. • Other parameters are calculated from the pixels in Sxy. • A general assumption is that ση 2 ≤ σL 2. • This is true because we assume that our noise is additive and position independent as the subimge is the subset of g(x, y).

Behavior of a filter • Here if the estimate of ση 2 is too low, then the algorithm will return an image that resembles the original image as the correction factors are too small. • If the estimates are too high, the ratio of the variances need to be clipped at 1. 0 and the algorithm will subtract the man from the image more frequently than it would normally do so. • If negative values are permitted, the image is rescaled at the end and the result is a loss of dynamic range.

% Read a gray scale image and add gaussian noise with 0 mean then apply % the Adaptive local noise reduction filter. clear all; close all; clc; f = imread('cameraman. tif'); f = im 2 double(f); [m n]=size(f); f 1=zeros(m, n); f = imnoise(f, 'gaussian', 0, 0. 1); D = std 2(f); M = mean 2(f); for i=3: m-2 for j=3: n-2 con=0; s 1=0; for k=i-2: i+2 for p=j-2: j+2 con=con+1; s = s+f(k, p); s 1(con)=f(k, p); end lm=s/con; ld = std(s 1); if ld >0 f 1(i, j) = f(i, j)-((D*(f(i, j)-lm)/ld)); else f 1(i, j) = f(i, j)-0; end end figure, imshow(f), title('Gaussian Noise Image'); figure, imshow(f 1), title('Adaptive Local Noise Filtered');

Adaptive median filter • The median filter works well if the spatial density of impulse noise is not large (if Pa and Pb are less than 0. 2). • But adaptive median filters can handle impulse noises of greater strength. • Adaptive median filter preserve the detail while smoothing nonimpulse noise, which is not done by normal median filter. • The adaptive median filter changes (increases) the size of Sxy during the filter operation. • The output of a median filter is a single value replacing the value of the pixel at (x, y), the point at which the window is centered.

Adaptive median filter • Let zmin, zmax = minimum and maximum gray level value in Sxy • zmed = median of gray level value in Sxy • zxy = gray level at coordinates (x, y) • Smax = maximum allowed size of Sxy

Working of adaptive median filter • The adaptive median filter works in 2 levels, called as level A and level B. • Level A : A 1 = zmed - zmin • A 2 = zmed – zmax • If A 1 > 0 AND A 2 < 0, Go to level B • Else increase the window size • If window size ≤ Smax repeat level A • Else output zxy. • Level B : B 1 = zxy - zmin • B 2 = zxy – zmax • If B 1 > 0 AND B 2 < 0, output zxy. • Else output zmed.

Working of adaptive median filter • • This algorithm does 3 things: Removes slat and pepper noise (impulse noise) Smoothing other non-impulsive noises. Reduce distortion such as excessive thinning or thickening of object boundaries. • The purpose of level A is to find if the median filter output, zmed is an impulse (black and white) or not. If the condition zmin < z med < zmax holds, then z med cannot be an impulse noise.

Working of adaptive median filter • Now we go to level B and test whether the center pixel zxy itself is an impulse. • If B 1 > 0 AND B 2 < 0 is true, then zmin < zxy < zmax and zxy cannot be an impulse. • Now the output of the algorithm is unchanged pixel value zxy. • By not changing these “intermediate level” points, distortion is reduced in the image. • If the condition B 1 > 0 AND B 2 < 0 is false, then either zxy = zmin or zxy = zmax. • In both the cases, the value of the pixel is an extreme value and the algorithm outputs the median value zmed which we know from level A is not a noise impulse.