Restoration With Image Restoration one tries to repair

Restoration With Image Restoration one tries to repair errors or distortions in an image, caused during the image creation process. In general our starting point is a degradation and noise model: g(x, y) = H ( f(x, y) ) + (x, y) Determined by quality of equipment and image taking conditions: • image restoration is computationally complex • equipment as degradation free as possible • seen technical and financial limitations • medical: low radiation, little time in magnet-tube • lowest image quality to achieve medical goals • web-cams: cheap lens distortions corrected by CPU in cam 2007 Theo Schouten 1

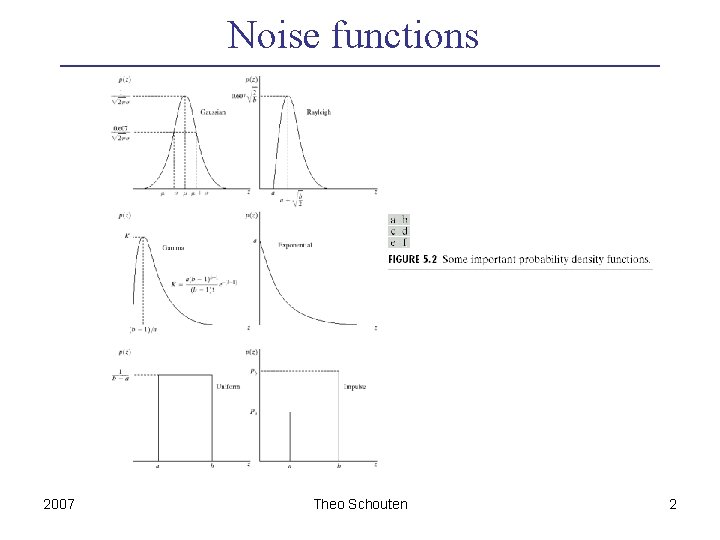
Noise functions 2007 Theo Schouten 2

Only noise See also enhancement, mean and median filters 2007 Theo Schouten 3

Mars, mariner 6 2007 Theo Schouten 4

Linear degradation When the degradation process is linear: H( k 1 f 1 + k 2 f 2 ) = k 1 H( f 1) + k 2 H( f 2 ) we can write (we temporarily leave the noise out of consideration): g(x, y) = H(f(x, y)) = H( f( , ) (x- , y- ) d d ) = f( , ) H( (x- , y- ) ) d d = f( , ) h(x, , y, ) d d h(x, , y, ) is the "impulse response" or "point spread function", the degraded image of an ideal light point. The integral is called the "superposition“ or "Fredholm” integral of the first kind. 2007 Theo Schouten 5

Position invariant, inverse filtering When H is a spatial invariant: Hf(x- , y- )=g(x- , y- ) then: h(x, , y, ) = h(x- , y- ) and g(x, y) = f( , ) h(x- , y- ) d d a convolution integral, and taking into account the noise: G(u, v) = H(u, v)F(u, v) + N(u, v) Inverse filtering: G(u, v)/H(u, v) = F(u, v) + N(u, v)/H(u, v) Problems: if H(u, v) = 0, or small: noise is blown up pseudo-inverse filter: use only parts of H(u, v) 2007 Theo Schouten 6

Degradation function by experiment 2007 Theo Schouten 7

by modelling H(u, v)= exp( -k(u 2+v 2)5/6 ) atmosferic turbulence model 2007 Theo Schouten 8

by calculation, linear motion Suppose a movement of the image during shutter opening: g(x, y) = 0 T f(x-x 0(t), y-y 0(t)) dt G(u, v) = [ 0 T f(x-x 0(t), y-y 0(t)) dt ] e -j 2 (ux+vy) dxdy = F(u, v) 0 T e -j 2 [uxo(t)+vy 0(t)] dt = F(u, v) H(u, v) With linear motion x 0(t)=at/T and y 0(t)=bt/T : H(u, v) = {T/[ (ua+vb)] } sin[ (ua+vb)] e -j [ua+vb] This has a lot of 0’s : (ua+vb) = n (any integer) pseudo-inverse filter is useless 2007 Theo Schouten 9

Linear motion blur 2007 Theo Schouten 10

Pseudo-inverse filter 2007 Theo Schouten 11

Gaussian movement A 1 -D Gaussian kernel for distortions in the horizontal direction. The intensity of each pixel is spread out over the neighboring pixels according to this kernel. Power spectrum Inverse filter 2007 Theo Schouten 12

with noise Uniform noise [0, 1] added (rounding floating point to unsigned byte) Movement lines disappear due to noise Inverse filter: nothing Pseudo-inverse filter, only when H(u, v) > T 2007 Theo Schouten 13

Wiener filtering minimum mean square error: e 2 = E{ (f-fc)2} Fc(u, v) =[1/H(u, v)] [ |H(u, v|2 / (|H(u, v|2 +S (u, v)/Sf(u, v))] G(u, v) S (u, v) = |N(u, v)|2 power spectrum of noise Approximations of S (u, v)/Sf(u, v): K (constant) |P(u, v)|2 (power spectrum of Laplacian) found by iterative method to minimize e 2 (constrained least squares filtering) 2007 Theo Schouten 14

Example Wiener filter Original Noise added Pseudo-inverse Wiener filter 2007 Theo Schouten 15

Linear motion Wiener filter 2007 Theo Schouten 16

Geometric distorsion Lenses often show a typical pincushion or barrel deviation. When the projection function x'=g(x) is known, for each measured pixel it can be determined from which parts of ideal pixels it is buit up. If the inverse function g-1 is known, then for each ideal pixel we can determine from which parts of the distorted pixels it is built up of. 2007 Theo Schouten 17

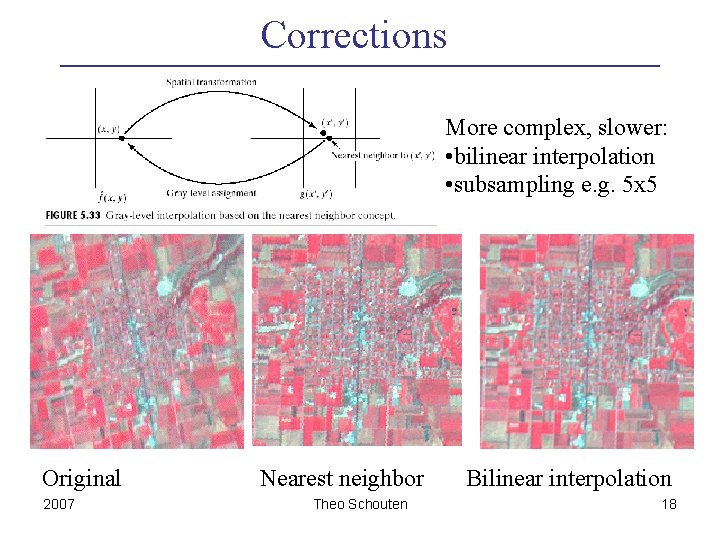
Corrections More complex, slower: • bilinear interpolation • subsampling e. g. 5 x 5 Original Nearest neighbor Bilinear interpolation 2007 Theo Schouten 18

Calibration, e. g. x’ = a +b x +c y and y’ = r +s x +t y : affine transformations Also higher order terms like d x 2 + e y 2 + f xy 2007 Theo Schouten 19

Fish eye lens x' = x + x*(K 1*r 2 + K 2*r 4 + K 3*r 6) + P 1*(r 2 + 2*x 2) + 2*P 2*x*y y' = y + y*(K 1*r 2 + K 2*r 4 + K 3*r 6) + P 2*(r 2 + 2*y 2) + 2*P 1*x*y 2007 Theo Schouten 20