50 th Anniversary of The Curse of Dimensionality































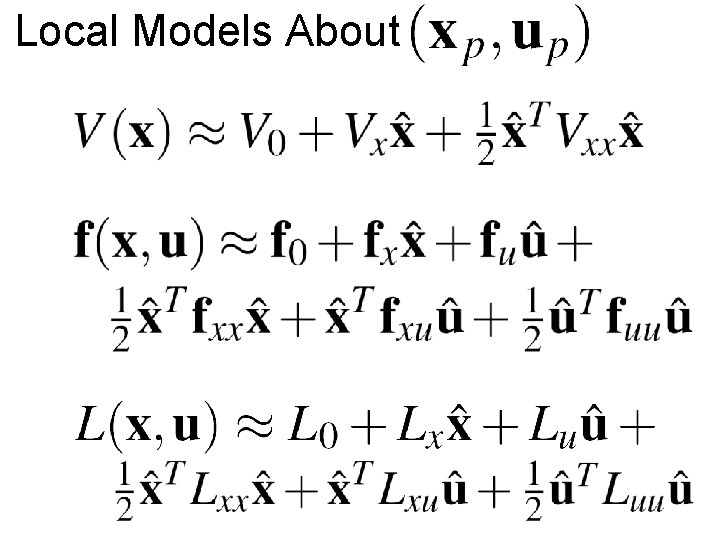

![Differential Dynamic Programming (DDP) [Mc. Reynolds 70, Jacobson 70] Value function (update) Execution Improved Differential Dynamic Programming (DDP) [Mc. Reynolds 70, Jacobson 70] Value function (update) Execution Improved](https://slidetodoc.com/presentation_image/400e3456dd085188d8e4390d34f959ec/image-51.jpg)











- Slides: 79

50 th Anniversary of The Curse of Dimensionality • Continuous States: Storage cost: resolutiondx Computational cost: resolutiondx • Continuous Actions: Computational cost: resolutiondu

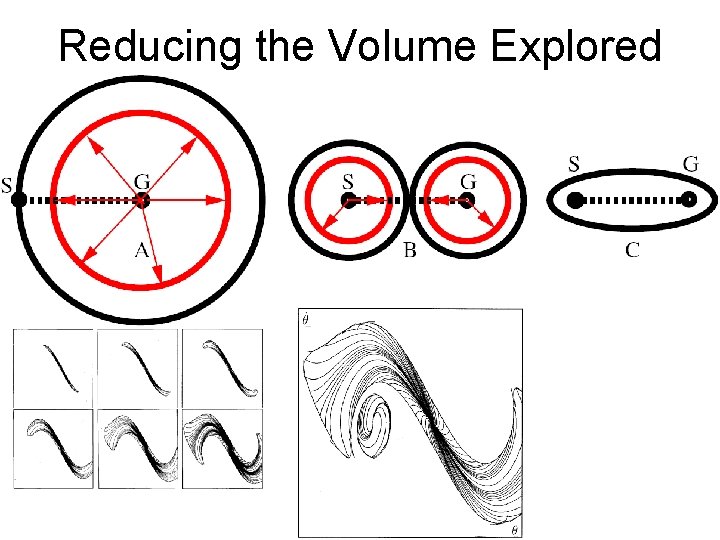
Beating The Curse Of Dimensionality • • • Reduce dimensionality (biped examples) Use primitives (Poincare section) Parameterize V, policy (future lecture) Reduce volume of state space explored Use greater depth search Adaptive/Problem-specific grid/sampling – Split where needed – Random sampling – add where needed • Random action search • Random state search • Hybrid Approaches: combine local and global opt.

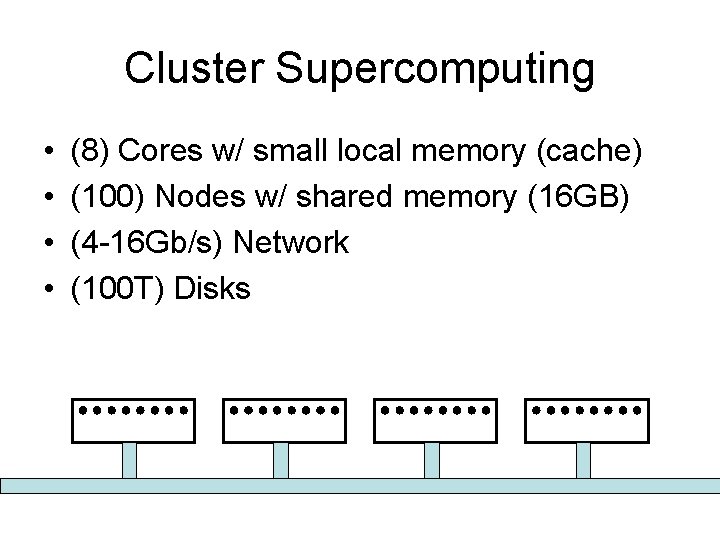
Use Brute Force • Deal with computational cost by using cluster supercomputer. • Main issue is minimizing communication between nodes.

Cluster Supercomputing • • (8) Cores w/ small local memory (cache) (100) Nodes w/ shared memory (16 GB) (4 -16 Gb/s) Network (100 T) Disks

Q(x, u) = L(x, u) + V(f(x, u)) • c = L(x, u): as in desktop case • x_next = f(x, u): as in desktop case • V(x_next) – Uniform grid – Multilinear interpolation if all values available, distance weighted averaging if bad values

Allocate grid to cores/nodes

Handle Overlap

Push Updated V’s To Users

So what does this all mean for programming? • On a node, split grid cells among threads, which execute on cores. • Share updates of V(x) and u(x) within node almost for free using shared memory. • Pushing updated V(x) and u(x) to other nodes uses the network which is relatively slow…. .

Dealing with the slow network • Organize grid cells into packet-sized blocks. Send them as a unit. • Threshold updates: too small, don’t send it. • Only do 1/N updates for each block (maximum skip time). • Tolerate packet loss (UDP) vs. verification (TCP/MPI)

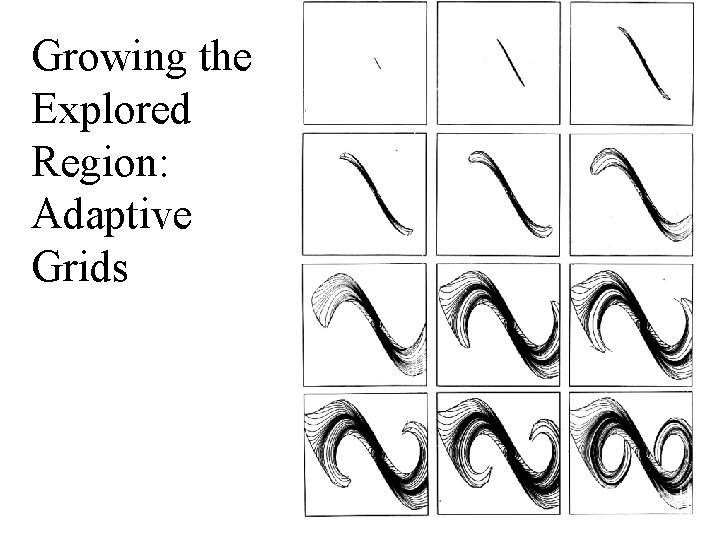
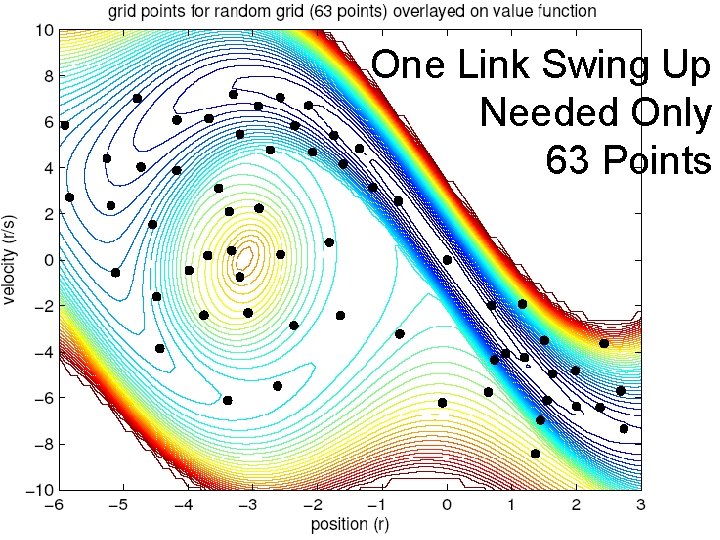
Use Adaptive Grid • Reduce computational and storage costs by using adaptive grid. • Generate adaptive grid using random sampling.

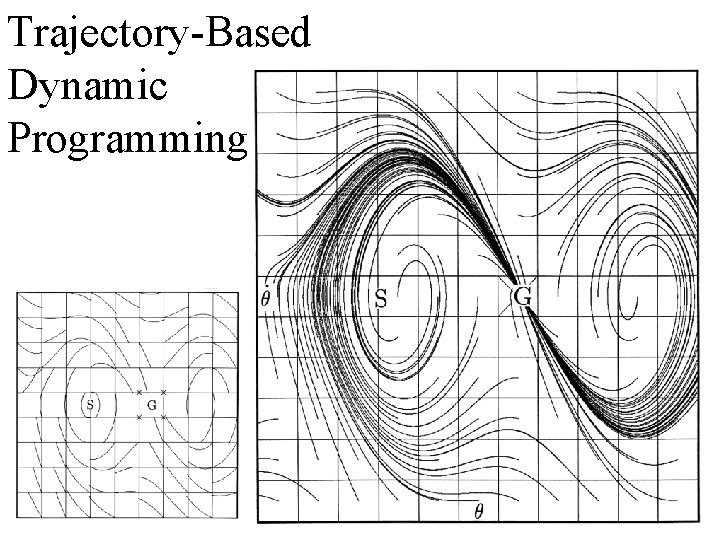
Trajectory-Based Dynamic Programming

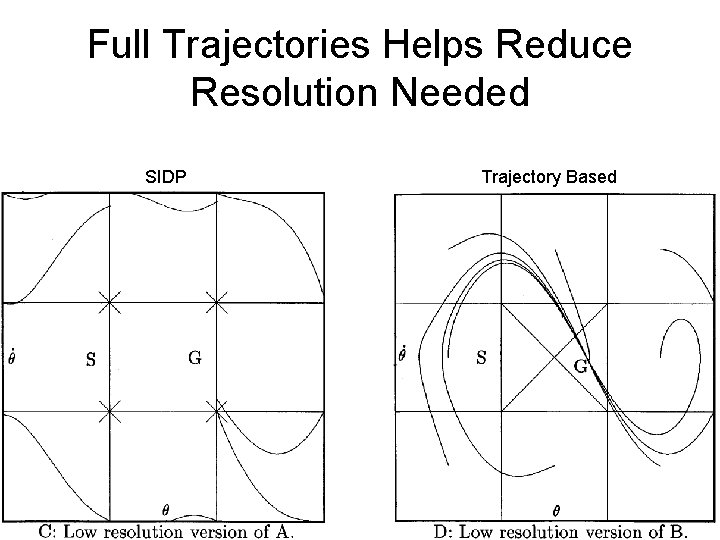
Full Trajectories Helps Reduce Resolution Needed SIDP Trajectory Based

Reducing the Volume Explored

An Adaptive Grid Approach





Global Planning Propagate Value Function Across Trajectories in Adaptive Grid

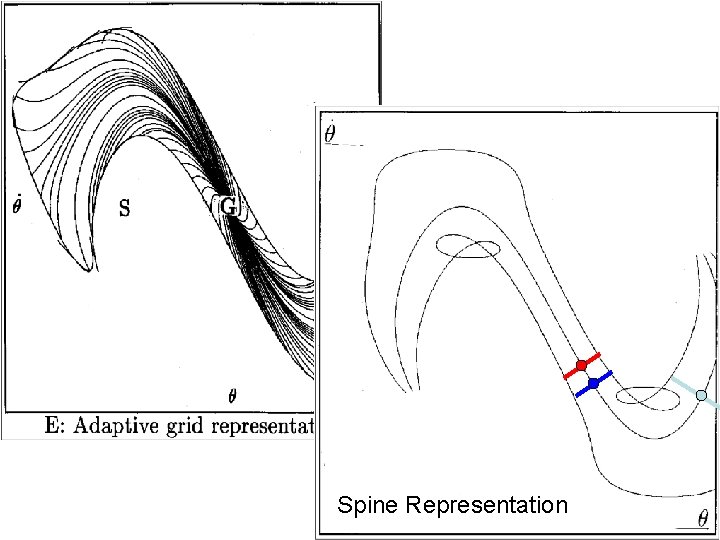
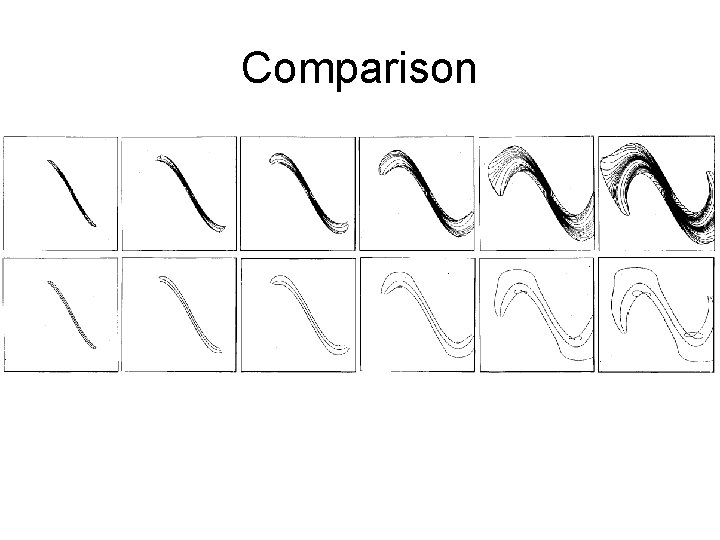
Growing the Explored Region: Adaptive Grids

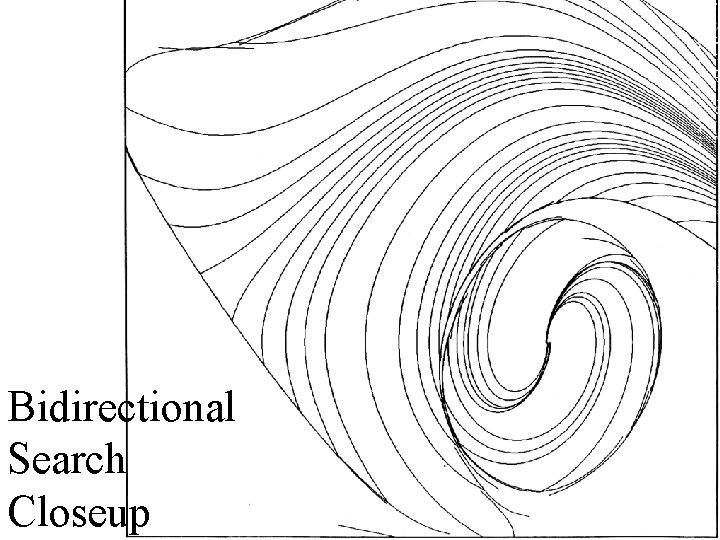
Bidirectional Search

Bidirectional Search Closeup

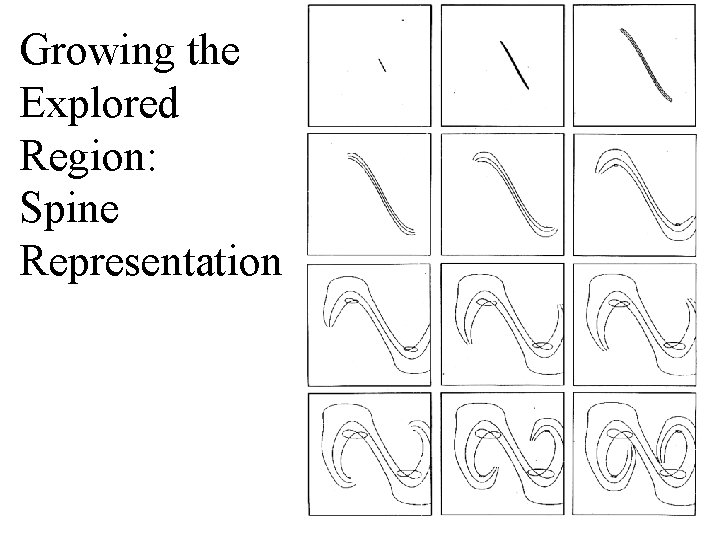
Spine Representation

Growing the Explored Region: Spine Representation

Comparison


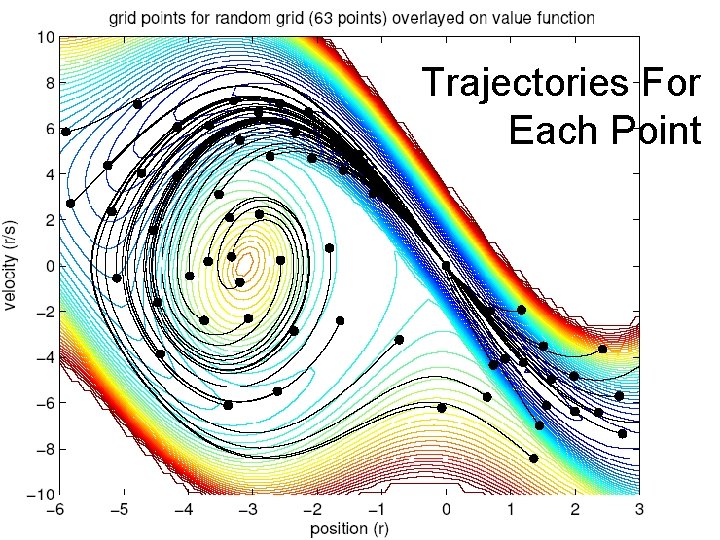
One Link Swing Up Needed Only 63 Points

Trajectories For Each Point

Random Sampling of States • Initialize with a point at the goal with local models based on LQR. • Choose a random new state x. • Use the nearest stored point’s local model of the value function to predict the value of the new point (VP). • Optimize a trajectory from x to the goal. At each step use the nearest stored point’s local model of the policy to create an action. Use DDP to refine this trajectory. VT is cost of trajectory starting from x. • Store point at start of trajectory if |VT - VP |> λ (surprise), VT < Vlimit and VP < Vlimit, otherwise discard. • Interleave re-optimization of all stored points. Only update if Vnew < V (V is upper bound on value). • Gradually increase Vlimit.

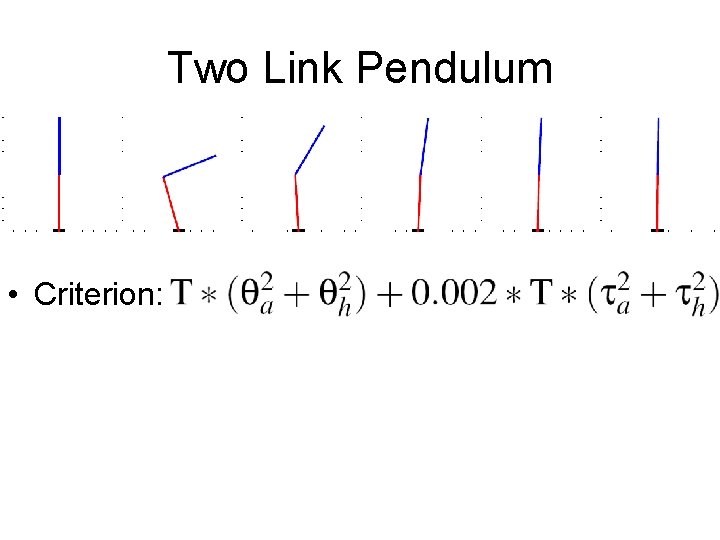
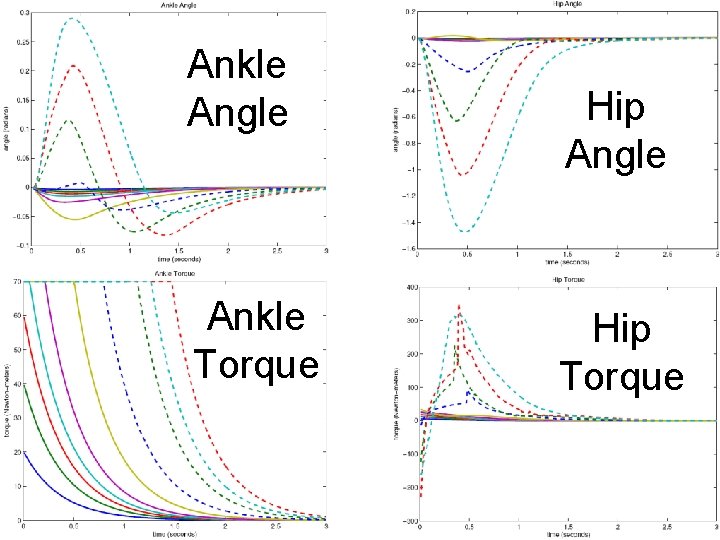
Two Link Pendulum • Criterion:


Ankle Angle Ankle Torque Hip Angle Hip Torque



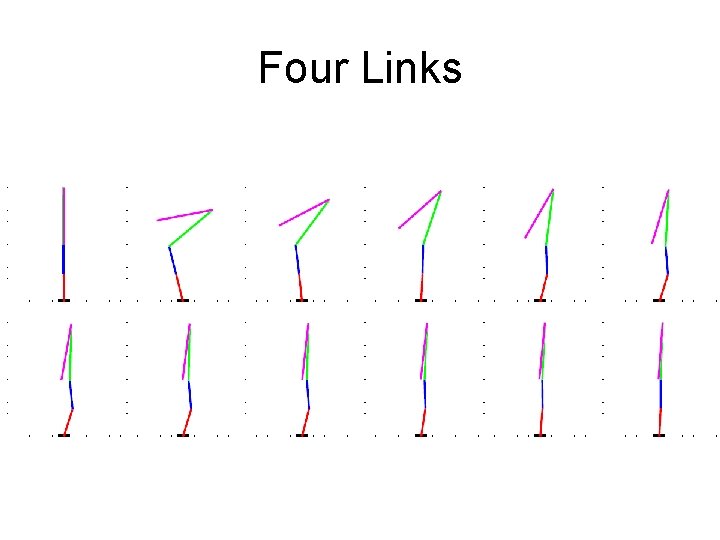
Four Links

Four Links: 8 dimensional system


Convergence? • Because we create trajectories to the goal, each value function estimate at a point is an upper bound for the value at that point. • Eventually all value function entries will be consistent with their nearest neighbor’s local model, and no new points can be added. • We are using more aggressive acceptance tests for new points: VB < λVP, λ < 1, and VP < Vlimit vs. |VB – VP| < ε and VB < Vlimit • Not clear if needed new points can be blocked.

Use Local Models • Try to achieve a sparse representation using local models.

Linear Quadratic Regulators

Learning From Observation

Regulator tasks • Examples: balance a pole, move at a constant velocity • A reasonable starting point is a Linear Quadratic Regulator (LQR controller) • Might have nonlinear dynamics xk+1 = f(xk, uk), but since stay around xd, can locally linearize xk+1 = Axk + Buk • Might have complex scoring function c(x, u), but can locally approximate with a quadratic model c x. TQx + u. TRu • dlqr() in matlab

Linearization Example • • • Iθdd = -mgl sin(θ) – μθd + τ Linearize Discretize time Vectorize (θ θd) k+1 T = (1 T; -mgl. T/I 1 -μT/I) (θ θd) k. T + (0 T/I)T τk

LQR Derivation • • Assume V() quadratic: Vk+1(x) = x. TVxx: k+1 x C(x, u) = x. TQx + u. TRu + (Ax+Bu)TVxx: k+1 (Ax+Bu) Want C/ u = 0 BTVxx: k+1 Ax = -(BTVxx: k+1 B + R)u u = Kx (linear controller) K = - (BTVxx: k+1 B + R)-1 BTVxx: k+1 A Vxx: k= ATVxx: k+1 A + Q + ATVxx: k+1 BK

Trajectory Optimization (closed loop) • Differential Dynamic Programming (local approach to DP).

Learning Trajectories

Q function • • x: state, u: control or action Dynamics: xk+1 = f(xk, uk) Cost function: L(x, u) Value function V(x) = ∑L(x, u) Q function Q(x, u) = L(x, u) + V(f(x, u)) Bellman’s Equation V(x) = minu Q(x, u) Policy/control law: u(x) = argminu Q(x, u)
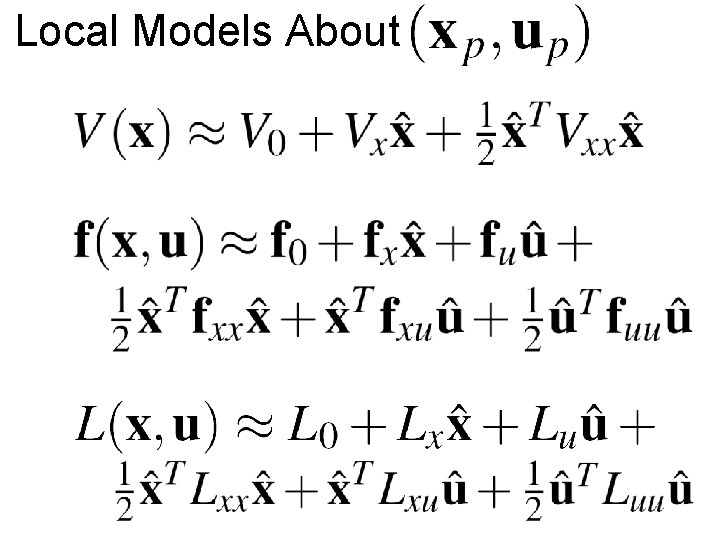
Local Models About

Propagating Local Models Along a Trajectory: Differential Dynamic Programming Gradient version • Vx: k-1 = Qx = Lx + Vxfx • Δu = Qu = Lu + Vxfu
![Differential Dynamic Programming DDP Mc Reynolds 70 Jacobson 70 Value function update Execution Improved Differential Dynamic Programming (DDP) [Mc. Reynolds 70, Jacobson 70] Value function (update) Execution Improved](https://slidetodoc.com/presentation_image/400e3456dd085188d8e4390d34f959ec/image-51.jpg)
Differential Dynamic Programming (DDP) [Mc. Reynolds 70, Jacobson 70] Value function (update) Execution Improved trajectory Terminal V(T) Initial Require: • Dynamics model • Penalty function Nominal trajectory Q(T-2) u’(T-2) V(T-2) Q(T-1): Action value function u’(T-1): New control output V(T-1): State value function t

Propagating Local Models Along a Trajectory: Differential Dynamic Programming

Levenberg Marquardt • • • y = f(x) minx (s = y. Ty/2) gradient ∂s/∂x = (∂f/∂x)Ty = JTy Hessian ∂2 s/∂2 x = H = (∂2 f/∂2 x) y + JTJ 2 nd order gradient descent Δx = H-1 JTy Problem: H not positive definite Solution: Δx = (H + λI)-1 JTy λ small: 2 nd order approach λ large: 1 st order approach, Δx = JTy/λ Trick 2: H ≈ JTJ

Levenberg Marquardt-like DDP • Δu = (Quu + λI)-1 Qu • K = (Quu + λI)-1 Qux • Drop fxx, fxu, fux, and fuu terms

Other tricks • If Δu fails, try ε Δu • Just optimize last part of trajectory. • Regularize Qxx

Neighboring Optimal Control

What Changes When Task Periodic? • Discount factor means V() might increase along trajectory. V() cannot always decrease in periodic tasks.


Robot Hopper Example

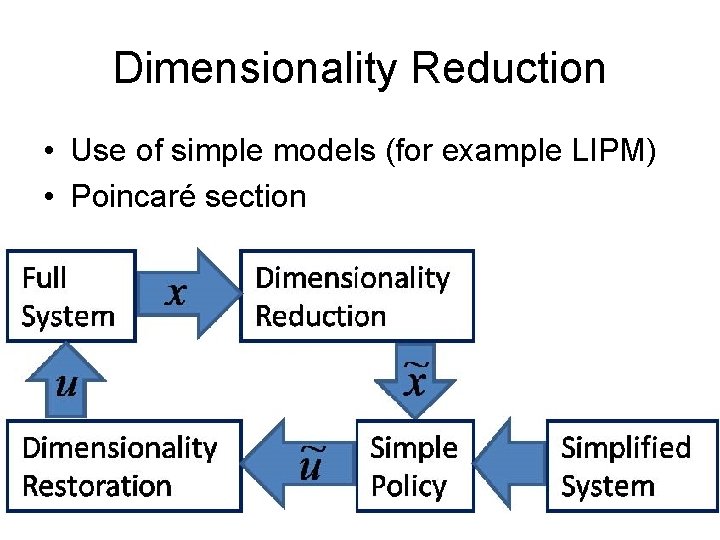
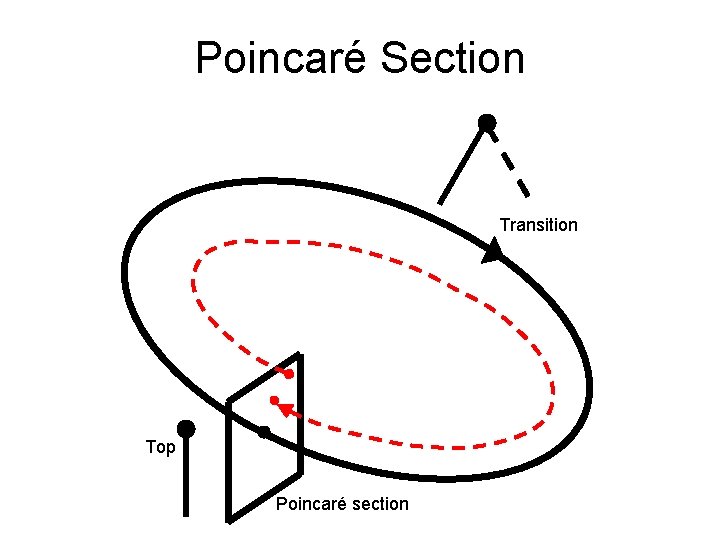
Dimensionality Reduction • Use of simple models (for example LIPM) • Poincaré section

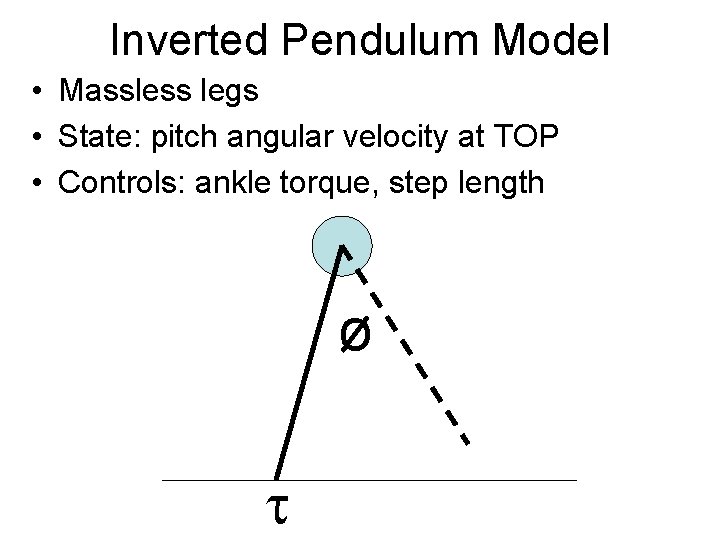
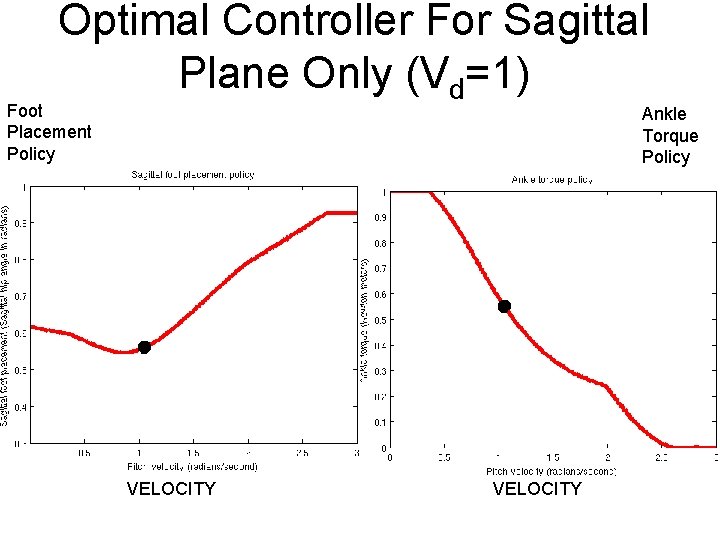
Inverted Pendulum Model • Massless legs • State: pitch angular velocity at TOP • Controls: ankle torque, step length ø

Optimization Criterion • T is step duration; Ta is ankle torque; ø is leg swing angle; Vd is desired velocity. • Ankle torque: ∑(Ta 2) • Swing leg acceleration: (ø/T 2)2 • Match desired velocity: (2 sin(ø/2)/T – Vd)2 • Criterion is weighted sum of above terms.

Poincaré Section Transition Top Poincaré section

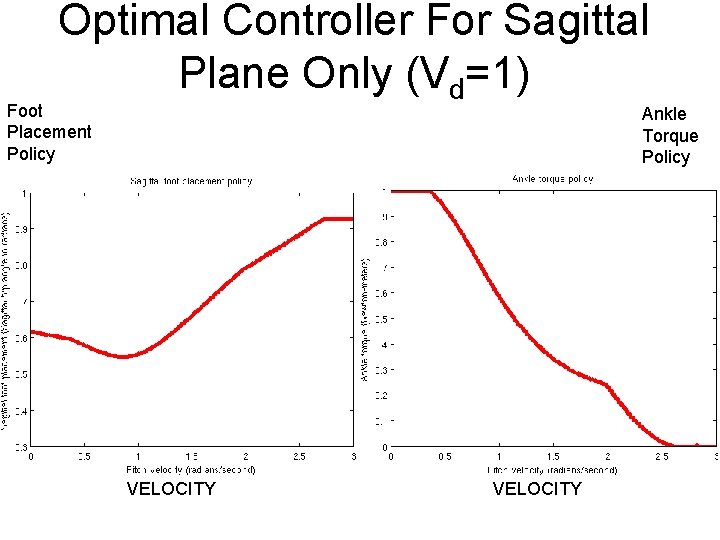
Optimal Controller For Sagittal Plane Only (Vd=1) Foot Placement Policy Ankle Torque Policy Return Map Value Function VELOCITY

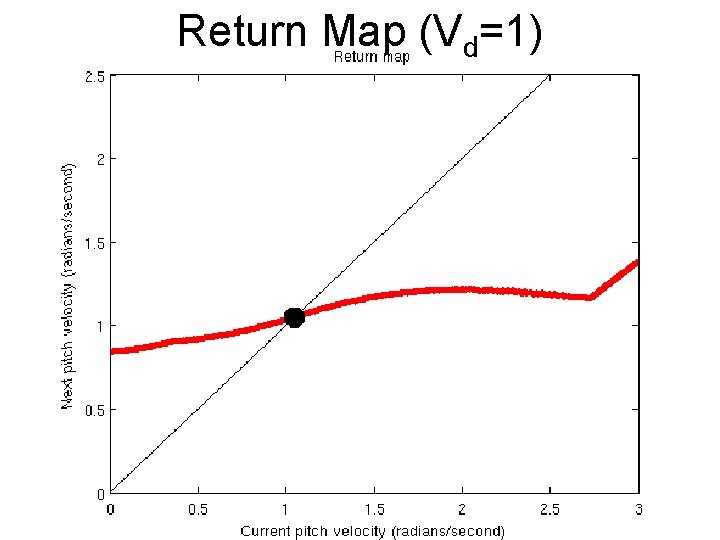
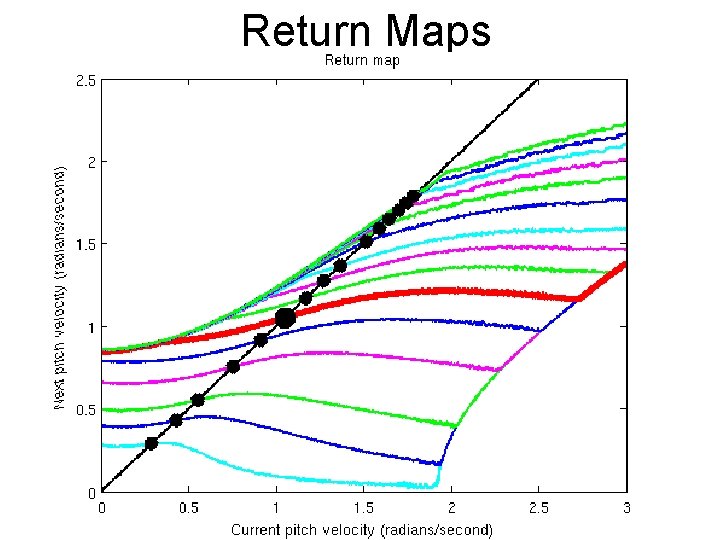
Return Map (Vd=1)

Optimal Controller For Sagittal Plane Only (Vd=1) Foot Placement Policy Ankle Torque Policy Return Map Value Function VELOCITY

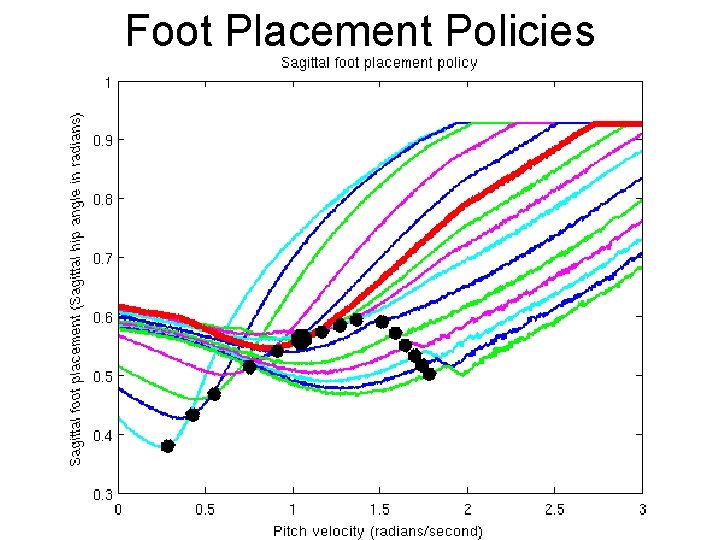
Foot Placement Policies

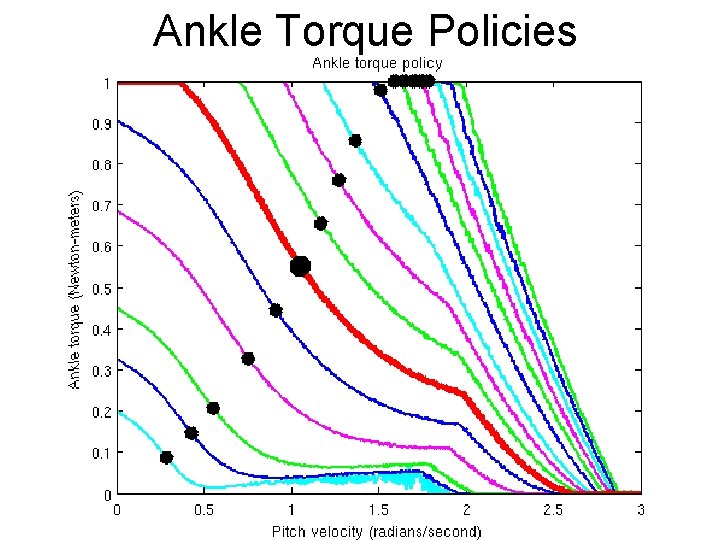
Ankle Torque Policies

Return Maps

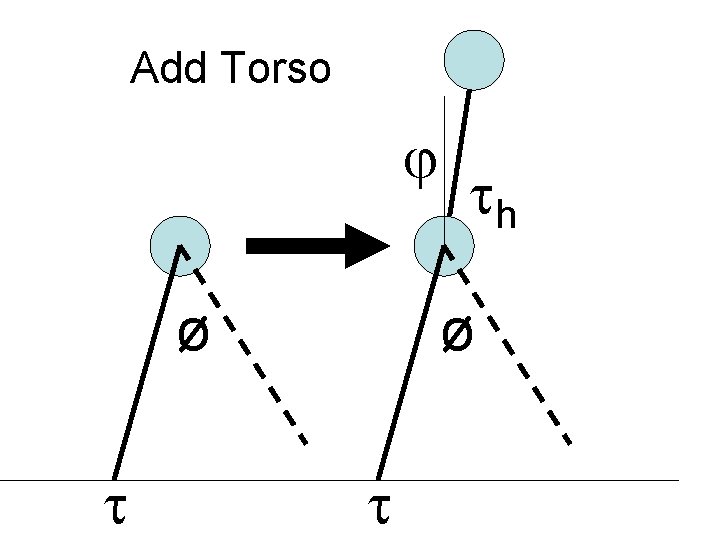
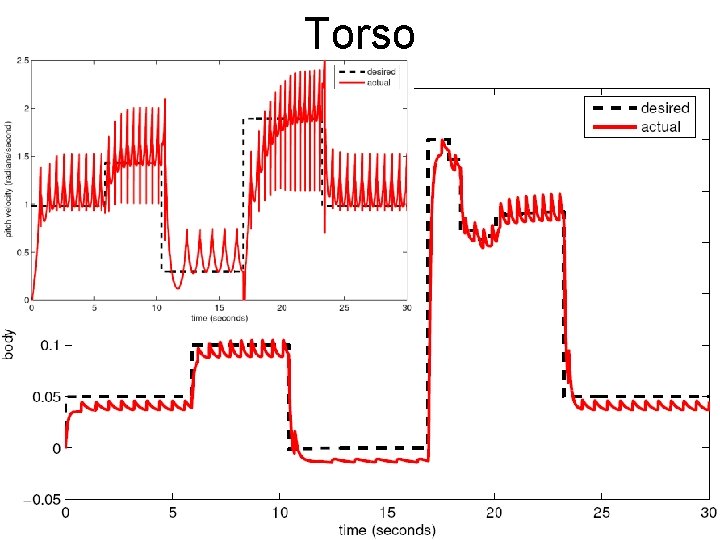
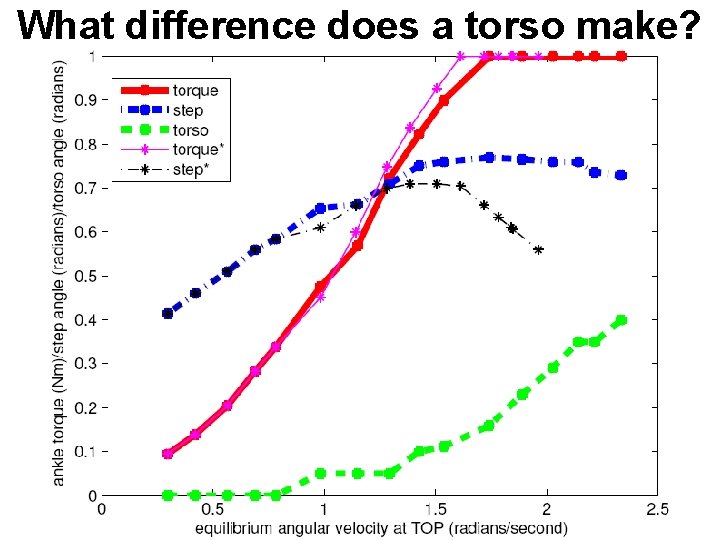
Add Torso ø h ø

Optimization Criteria • Ankle torque: ∑(Ta 2) • Swing leg acceleration: (ø/T 2)2 • Match desired velocity: (2 sin(ø/2)/T – Vd)2 • Desired torso angle: ∑(ψd)2

Simulation

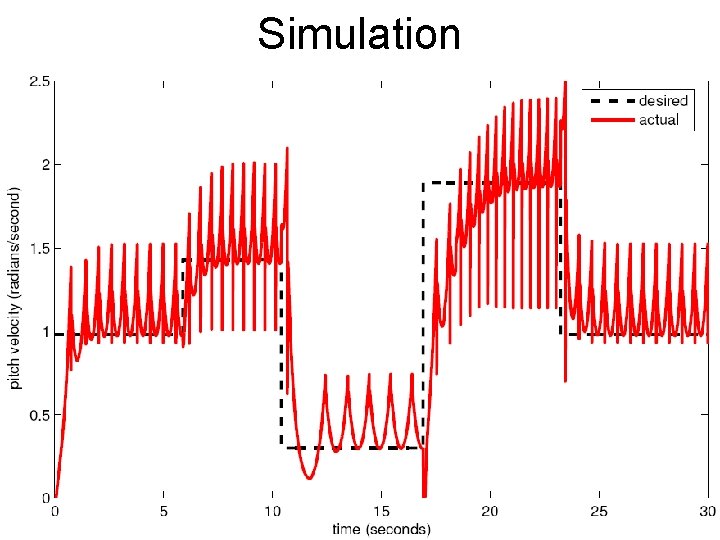
Simulation

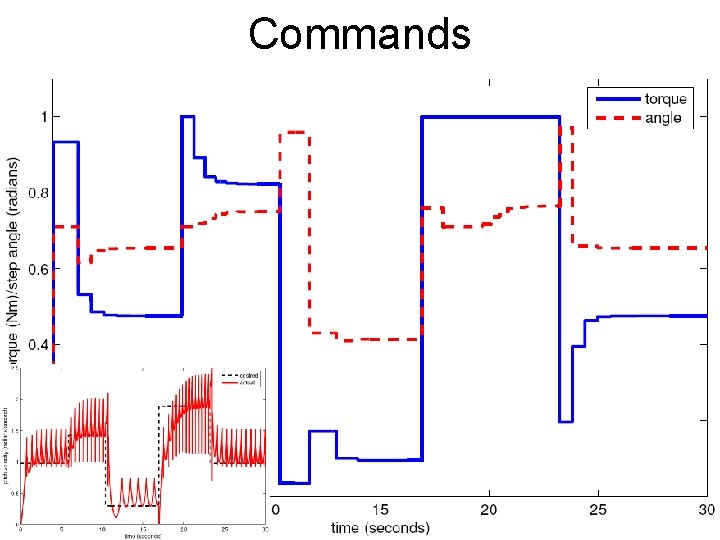
Commands

Torso

What difference does a torso make?

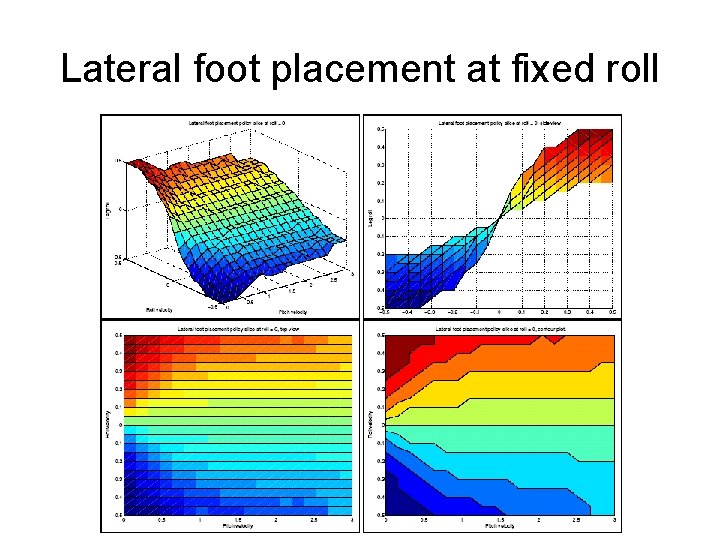
3 D version: Add roll • State: pitch velocity, roll velocity at TOP • Action 1: Sagittal foot placement • Action 2: Sagittal ankle torque • Action 3: Lateral foot placement

Roll Optimization Criteria • T = step duration. • Ankle torque: torque 2 • Swing leg acceleration: (ø/T 2)2 • Match desired velocity: (2 sin(ø/2)/T – Vd)2 • Roll leg acceleration: (øroll/T 2)2

Lateral foot placement at fixed roll
 Decision surface
Decision surface Plmar logo png
Plmar logo png Gay porn 10 year anniversary gangbang
Gay porn 10 year anniversary gangbang Reporter philip taggart visits a farm
Reporter philip taggart visits a farm Japan 47 artisans
Japan 47 artisans Types of attributes in data mining
Types of attributes in data mining K means dimensionality reduction
K means dimensionality reduction Blessing of dimensionality
Blessing of dimensionality Dimensionality reduction in machine learning
Dimensionality reduction in machine learning Nlp dimensionality reduction
Nlp dimensionality reduction Feature reduction in machine learning
Feature reduction in machine learning Dimensionality pronunciation
Dimensionality pronunciation Dimensionality
Dimensionality Act four scene one macbeth summary
Act four scene one macbeth summary Resource curse and dutch disease
Resource curse and dutch disease The curse of knowledge
The curse of knowledge Hope in christ alone
Hope in christ alone Quotes on greed is curse
Quotes on greed is curse Ciullare
Ciullare Curse clinet
Curse clinet Til on that cross as jesus died
Til on that cross as jesus died What is the curse of macbeth
What is the curse of macbeth Queen esther curse
Queen esther curse Manitou potatoes
Manitou potatoes Bath curse tablets
Bath curse tablets Jesus cursed the fig tree kjv
Jesus cursed the fig tree kjv Curse of ham apush
Curse of ham apush Devoveo
Devoveo Macbeth map
Macbeth map To which city does romeo go after being exiled
To which city does romeo go after being exiled Boddlebrooks
Boddlebrooks What is the curse of macbeth
What is the curse of macbeth Curse is the man who hangs on a tree
Curse is the man who hangs on a tree Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể đại từ thay thế
đại từ thay thế Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Môn thể thao bắt đầu bằng chữ f
Môn thể thao bắt đầu bằng chữ f Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Sự nuôi và dạy con của hổ
Sự nuôi và dạy con của hổ Các loại đột biến cấu trúc nhiễm sắc thể
Các loại đột biến cấu trúc nhiễm sắc thể Thế nào là sự mỏi cơ
Thế nào là sự mỏi cơ Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Phản ứng thế ankan
Phản ứng thế ankan Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Tia chieu sa te
Tia chieu sa te điện thế nghỉ
điện thế nghỉ Một số thể thơ truyền thống
Một số thể thơ truyền thống Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Sơ đồ cơ thể người
Sơ đồ cơ thể người Số nguyên là gì
Số nguyên là gì đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Glasgow thang điểm
Glasgow thang điểm ưu thế lai là gì
ưu thế lai là gì Tư thế ngồi viết
Tư thế ngồi viết Thẻ vin
Thẻ vin Cái miệng nó xinh thế
Cái miệng nó xinh thế Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Mật thư tọa độ 5x5
Mật thư tọa độ 5x5 Bổ thể
Bổ thể Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Tư thế ngồi viết
Tư thế ngồi viết V cc cc
V cc cc Thể thơ truyền thống
Thể thơ truyền thống Chúa yêu trần thế
Chúa yêu trần thế Khi nào hổ con có thể sống độc lập
Khi nào hổ con có thể sống độc lập Diễn thế sinh thái là
Diễn thế sinh thái là Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Cong thức tính động năng
Cong thức tính động năng 101012 bằng
101012 bằng Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Lời thề hippocrates
Lời thề hippocrates
































































































